淮河洪水概率预报方法研究及应用
2018-05-18蒋晓蕾
王 凯 蒋晓蕾
(淮河水利委员会水文局(信息中心) 蚌埠 233001 河海大学 南京 210098)
1 研究背景
水文预报是一种重要的防洪非工程措施,直接为防汛抗旱和水资源管理服务。目前广泛使用的水文预报模型大多是确定性的,模型以确定预报值的形式输出给用户。实际上,由于水文过程的影响因素复杂多变,加之人类认识水平的有限,使得水文预报过程中不可避免地存在着诸多的不确定性。目前,水文预报不确定性量化已逐渐成为了研究热点,概率预报作为其重要的表现形式,已成为了水文预报的发展趋势。
当前国内外关于洪水概率预报的研究主要包括两类途径:第一类是全要素耦合途径,分别量化降雨—径流过程各个环节的主要不确定性,如降雨输入不确定性、模型结构不确定性、模型参数不确定性等,并进行耦合,实现概率预报。如Kavetski等采用“潜在变量”雨深乘子(stormdepthmultiplier)反映降雨输入的不确定性,并将模型的敏感性参数随机化,应用马尔可夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)采样方法求解流量后验分布,提出贝叶斯总误差分析(Bayesian total error analysis,BATEA)方法。在国内,李明亮等基于层次贝叶斯模型(Bayesian hierarchical model),构建联合概率密度函数以考虑模型参数和降雨输入不确定性,并采用MCMC方法进行求解。梁忠民等借用抽站法原理推求降雨量的条件概率分布,进而实现考虑输入不确定性的洪水概率预报。全要素耦合途径能够溯源预报不确定性,但计算相对耗时,无法满足实时预报的需要。
第二类是总误差分析途径,即从确定性预报结果入手,直接对预报不确定性进行量化分析,推求预报量的分布函数,实现概率预报。Krzysztofowicz等提出的贝叶斯预报系统(Bayesian forecastingsystem,BFS)最具代表性,其中水文不确定性处理器(hydrologic uncertainty processor,HUP)在正态空间中对似然函数进行了线性假定,为推求预报量后验分布的解析表达提供了可能。王善序详细介绍了BFS的理论,并指出它可以综合考虑预报过程的不确定性,不限定预报模型的内部结构。近年来,很多研究表明,不同流量量级的预报不确定性存在差异。王晶晶等在原始空间中开展预报误差规律研究,发现不同流量量级的误差服从不同的分布函数,为此采用极小熵确定各分布线型,采用极大熵进行参数估计,进而降低了福建池潭水库管理的风险。Van Steenbergen等针对不同预见期、不同流量量级预报误差统计规律的差异,采用频率学方法,构建了三维误差矩阵,量化预报不确定性。
本文在第二类研究途径框架下,结合研究区域(淮河王家坝断面)预报误差的统计特征,假定误差均值随流量量级呈分段线性变化,在贝叶斯预报系统(BFS)的基础上,对其水文不确定性处理器(HUP)进行改进,提出改进的贝叶斯概率预报系统(PCA-HUP),定量评估单个水文模型预报结果的可靠度,实现概率预报。
2 模型方法
考虑误差异分布的洪水概率预报方法不涉及预报的中间环节,只对预报结果进行分析,定量评估预报结果的不确定性,并在此基础上实现洪水概率预报。在贝叶斯预报系统(BFS)的基础上,对其水文不确定性处理器(HUP)进行改进,提出改进的贝叶斯概率预报系统(PCA-HUP),定量评估单个水文模型预报结果的可靠度,实现概率预报。
2.1 HUP基本原理
水文不确定性处理器(Hydrologic UncertaintyProcessor,HUP)是贝叶斯概率预报系统(BFS)的主要组成部分,用以分析除降雨之外的其他所有不确定性。其特点是,不需要直接处理预报模型的结构与参数,而是从预报结果入手,分析其与实测水文过程的误差,再利用贝叶斯公式估计预报变量的概率分布,从而实现水文模型预报结果的不确定性分析及概率预报。其工作流程如图1所示。
2.2 改进的概率洪水预报PCA-HUP模型
为推求预报量后验分布的解析解,传统HUP模型结合亚高斯模型,在正态空间中对先验分布式和似然函数式进行线性假设,并采用最小二乘法对相关参数进行估计。
然而,由于似然函数式的自变量之间存在明确的线性关系,必然导致回归方程的多重共线性问题。若采用传统最小二乘法进行参数估计,会使得估计的回归系数不唯一,也使得回归方程不稳定(原始数据的极小变化可造成参数估计值和标准差的明显变化)。因此,项目研究结合主成分分析技术(Principal components analysis,PCA),对传统 HUP模型进行改进,提出PCA-HUP模型。
主成分回归的基本思想:对原始回归变量进行主成分分析,将线性相关的自变量,转化为线性无关的新的综合变量,采用新的综合变量建立模型回归方程。
(1)主成分分析
设 X=(X1,…Xp)T是 P 维随机向量,均值 E(X)=μ,协方差阵 D(X)=Σ。
考虑它的线性变换:

用矩阵表示为:


图1 水文不确定性处理器工作流程示意图
由式(2)可以将 P 个 X1,X2,…Xp转化为 P 个新变量,Z1,Z2,…Zp若新变量 Z1,Z2,…Zp满足下列条件:
1)Zi和 Zj相互独立,i≠j,i,j=1,2,…,p;
2)Var(Z1)≥Var(Z2)≥…≥Var(Zp);

则新变量 Z1,Z2,…Zp为 X1,X2,…Xp的 P 个主成分,且Z1,Z2,…Zp线性无关。
(2)主成分回归
实际问题中不同的变量经常具有不同的量纲,变量的量纲不同会使分析结果不合理,将变量进行标准化处理可避免这种不合理的影响。
对数据进行标准化首先要得出样本标准差和样本均值,记sj为xj样本标准差,即是 xj的样本均值,即原始数据的标准化变换为:

标准化后的数据矩阵为:

标准化后,X的相关系数阵也就是X的协方差阵(半正定矩阵):

其中:

采用Lagrange乘子法求解,可以求得:

其中:λ1≥λ2≥…≥λp≥0 为 R 的特征值,a1,a2,…ap是相对应的单位正交特征向量,ap=(a1pa2p,…app)T。
主成分回归可以得到p个主成分,这p个主成分之间互相独立,且方差呈递减趋势,所包含的自变量的信息也是递减的。即主成分对因变量的贡献率是递减的,第i个主成分Zi的贡献率可以用来表示。
在实际问题的分析时,由于主成分的贡献率是递减的,后面的主成分贡献率有时会非常小,所以一般不选取P个主成分,而是根据累计贡献率来确定主成分个数,即:前m个主成分的累计贡献率达到0.85时,选取前m个主成分进行回归。则原始回归问题转化为以下回归问题:
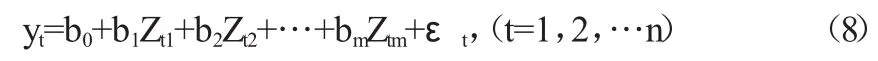
其中:E(εt)=0,Var(εt)=σ2,Cov(εi,εi)=0,(i≠j)
回归模型的矩阵形式为:

采用最小二乘法估计参数矩阵B,根据式(1)和式(3)可以估计因变量矩阵Y与自变量矩阵之间X的回归系数矩阵。
由此可见,主成分回归模型是对普通的最小二乘估计的改进,首先选取主成分,克服自变量间的多重共线性,然后对所选的主成分进行线性回归,进而得到主成分回归方程。
3 实例应用
3.1 研究区概况
王家坝站系淮河上游总控制站,集水面积30630km2。上游干流河长360km,河道比降0.5‰,年平均降水量800~1200mm,且降水年际变化大,时空分布不均匀。年降水量的60%集中在5~8月,以6、7两月暴雨次数较多。产生暴雨的主要天气系统是西南低涡、切变线、低压槽和台风等。淮干上游及淮南山区一般是王家坝洪水的主要来源区。本项目主要针对息县、潢川、班台至王家坝区间(面积为7110km2)开展研究,见图 2。
3.2 概率预报结果
本研究以新安江模型为确定性预报模型,在此基础上,采用PCA-HUP模型分别对上述模型预报的可靠度进行定量,并在淮河干流主要控制断面王家坝进行了实际应用,采取滚动预报方式实现了洪水概率预报。
将新安江模型的预报结果与实测资料输入PCA-HUP模型中,其中20场洪水用于相关参数的率定,8场洪水用于模型验证。模型相关参数见表1。以置信度为90%(亦可采用其他置信度值)的预报区间为例,对概率预报结果进行评估,同时,对流量分布函数的中位数Q50进行分位数评价,率定期模型的模拟精度见表2。
由表2可知,PCA-HUP模型率定期模拟结果:预报区间(置信度为90%)覆盖率较高,且离散度在0.2以内。此外,将每一时刻预报量概率分布的中位数预报与实测流量进行比较,确定性系数接近于1,洪峰误差在1%以内,说明中位数预报的精度非常高,且从不同预见期的模拟过程线中可以看出,随着预见期的逐渐增大,区间离散度呈现出递增的趋势。
采用验证期8场洪水对概率预报模型进行检验,推求预报流量的概率分布,实现王家坝断面的洪水概率预报。预报精度统计见表3,预报流量过程线以其中两场为例,预报流量过程线如图3~图4所示。
由表3和2场洪水概率预报过程线可知,PCA-HUP模型(以新安江模型为确定性预报模型)提供的概率预报结果:预报区间(置信度为90%)覆盖率在87%以上,且离散度在0.2以内,说明在相对较小的区间宽度内,预报区间仍然能够覆盖绝大多数实测数据,说明概率预报精度较高。此外,将每一时刻预报量概率分布的中位数预报与实测流量进行比较,确定性系数接近于1,洪峰误差在1%以内,说明中位数预报的精度非常高,明显高于新安江模型预报结果,充分体现了贝叶斯修正原理。从不同预见期的预报过程线中可以看出,随着预见期的逐渐增大,区间宽度呈现出递增的趋势。

表2 PCA-HUP模型率定期模拟精度统计表(王家坝,Δt=2h)

图2 王家坝断面控制区域图

表1 PCA-HUP模型参数表(王家坝)

图3 a 19920505号洪水预报过程线图(王家坝,Δt=2h)
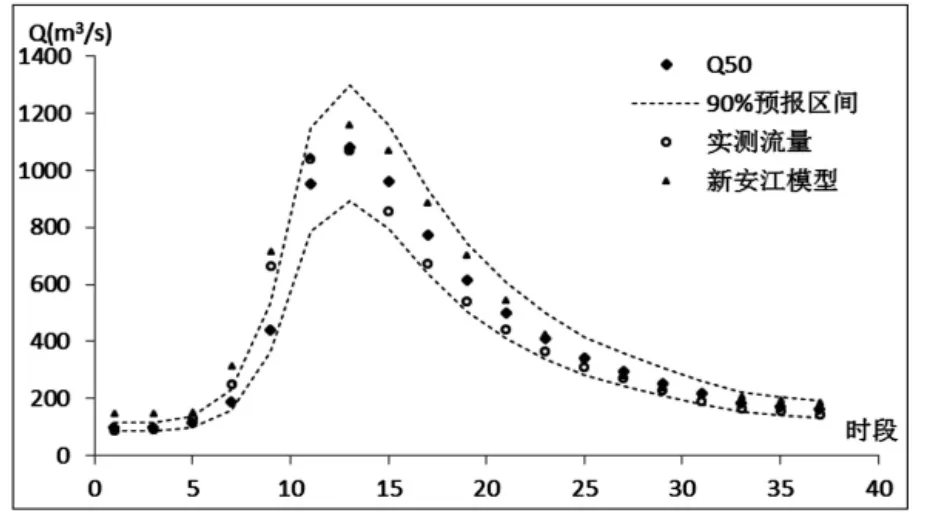
图3 b 19920505号洪水预报过程线图(王家坝,Δt=6h)

图3 c 19920505号洪水预报过程线图(王家坝,Δt=12h)

图4 a 19950707号洪水预报过程线图(王家坝,Δt=2h)

图4 b 19950707号洪水预报过程线图(王家坝,Δt=6h)
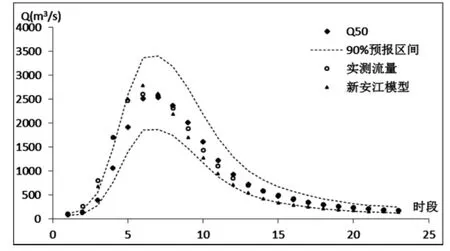
图4 c 19950707号洪水预报过程线图(王家坝,Δt=12h)

表3 PCA-HUP模型验证期概率预报精度统计表(王家坝,Δt=2h)
4 结论
本文在贝叶斯预报系统(BFS)的基础上,对其水文不确定性处理器(HUP)进行改进,提出改进的贝叶斯概率预报系统(PCA-HUP),PCA-HUP模型是在正态空间中对预报误差进行分析,构造线性似然函数,推求预报流量的后验分布,实现洪水概率预报。以淮河王家坝断面的洪水预报为示例进行了应用研究,表明该方法不仅可以提供不同置信度的区间预报结果,还可以获得精度更高的定值预报结果。
该方法可以与任何确定性的水文预报模型相耦合。作为示例,文中对相对误差进行了正态假设,但研究方法不局限于此,同样适用于误差服从其他分布的情况。限于研究区的预报误差特征,本文仅考虑了误差均值随流量量级的变化规律,相同思路亦适用于误差方差等分布参数随流量变化的情况■
