一种结合Rosenbrock算法的混合MIMIC算法及其应用
2018-05-18夏桂梅赵晋彬
夏桂梅,张 丹,赵晋彬
(太原科技大学应用科学学院,太原 030024)
MIMIC算法是一种依赖于解空间分布,具有较强全局搜索能力的分布估计算法, Rosenbrock算法是一种局部求精能力强的的优化算法。本文将MIMIC算法与Rosenbrock算法相结合,提出一种结合Rosenbrock算法的混合MIMIC算法——Rb-MIMIC算法,并将其应用在蜗杆传动优化设计中。
蜗杆传动是一种具有传动比大,结构紧凑,传动平稳,可实现自锁等优点的空间啮合传动,用于在空间交错的两轴间传递运动和动力。蜗杆传动在机床,汽车,起重机械等很多领域中发挥着重要的作用。通常采用碳钢或合金钢制蜗杆,采用青铜铸造蜗轮,这样可以使传动副具有良好的耐磨性,但是在制造过程中往往因为设计问题造成有色贵重金属的浪费。为了减少浪费,降低成本,将蜗轮齿圈体积最小作为优化设计目标[1-4]。本文采用结合了Rosenbrock算法的MIMIC算法对蜗杆金属圈体积进行参数优化,取得了良好的优化结果。
1 结合Rosenbrock法的混合MIMIC算法
1.1 MIMIC算法
MIMIC(Mutual Information Maximization for Input Clustering)算法,是在1997年由美国MIT人工智能实验室的De Bonet等人提出的一种基于双变量相关模型的分布估计算法[5]。算法通过在初始群体中建立一个概率模型,使得该模型可以描述解的分布,然后对概率模型进行随机采样来产生新的种群,如此反复进行,实现种群的进化,直至得到满意解6]。
在MIMIC算法中定义解空间概率分布模型:

其中,h(X)=-∑xP(X=x)logp(X=x),
h(X|Y)=-∑yh(X|Y=y)p(Y=y)
h(X|Y=y)=
-∑x(p(X=x|Y=y)logp(X=x|Y=y))
MIMIC算法的过程是一个不断更新概率模型,从而使概率模型越来越能反映优秀个体的分布的过程,所以算法在进化过程中,过于依靠解空间分布,导致算法在后期的进化过程中速度变慢,种群的多样性减少,这说明MIMIC算法具有比较强的全局搜索能力,但是局部求精能力较弱且易早熟。为了有效提高MIMIC算法的寻优能力,本文是在种群的进化过程中加入了局部求精能力强,收敛速度快的旋转方向法(Rosenbrock),提出一种结合Rosenbrock法的分布估计算法(Rb-MIMIC).
1.2 Rb-MIMIC算法
旋转方向法又称转轴法,是Rosenbrock于1960年提出的,Rosenbrock法是在当前点构造n个正交方向,然后在构造的每个方向进行探测移动,找到函数值减小最快的方向,移动某个步长,然后利用轴向的旋转产生一组新的方向作为下一次迭代的轴向,如此循环[7]。Rosenbrock法是一种局部搜索算法,具有较强的局部求精能力,而MIMIC算法的全局寻优能力强,但局部搜索能力较弱,易早熟,所以在MIMIC算法进化过程中可以加入Rosenbrock法来提高算法的寻优能力和效率。在MIMIC算法中,由于新个体的产生规则单一,导致新群体个性差异较小,为了增加种群的个性差异,同时又不背离群体的分布模型,在生成新的群体时,从当前群体中随机选择出部分个体利用Rosenbrock法进行搜索,将得到的新个体作为新群体中的一部分。具体步骤如下
步1 初始化群体。随机产生N个个体作为初始群体pop.
步2 将约束优化问题转化为无约束优化问题[8-9],这里利用罚函数法。
步3 评价适应值。计算种群中每个个体的适应值,如果满足算法的终止条件,则算法结束,否则转至下一步。算法的终止条件为达到规定的进化代数(200代),或者连续若干代(25代)最优值没有变化,或者误差在某个范围内(10-10).
步4 选择优势群体。算法采用截断法和轮盘赌法选择S(N/2)个个体作为优势群体,并保留p个最优个体。
步5 Rosenbrock法搜索。从当前群体中随机选择T个个体作为初始点进行Rosenbrock搜索,将得到的新个体作为新一代群体的一部分,增加种群的多样性。
步6 根据贪婪算法寻找最优排列构建概率模型。
1)使用in=argminjhl(Xj),找出排列θ=(i1,i2,…in)中的in;
2)对任意k=n-1,…,1,由式ik=argminjhl(Xj|Xk+1),其中k≠ik+1,…,in,计算出排列θ=(i1,i2,…in);
3)计算出概率分布
步7 采样得到新个体。按逆序的方法依据概率模型采样N-T-p次,与步3保留的p个最优个体及Rosenbrock法得到的T个个体组成新一代群体,转步2.
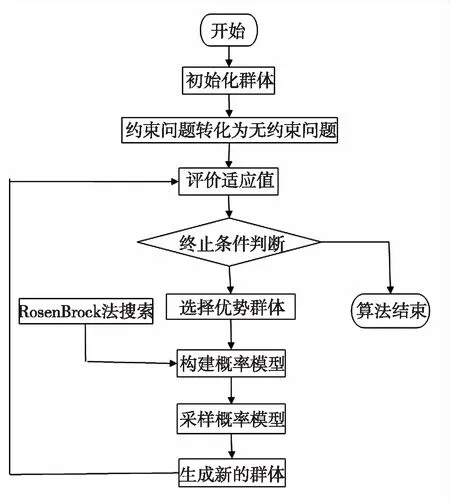
图1 算法流程图
Fig.1 Basic flow chart of algorithm
2 应用实例
以某单级普通圆柱蜗杆齿轮减速器为例3],它的输入功率P1=6 kW,转速n1=1 450 r/min,传动比i=20,载荷系数K=1.1,蜗轮齿圈许用接触应力[σH]=220 MPa.
2.1 构建数学模型
图2所示的是蜗轮齿圈尺寸结构示意图,包括:

图2 蜗轮齿圈结构示意图
Fig.2 Worm gear ring structure diagram
齿顶圆直径da、齿根圆直径df、齿圈内径d0、齿圈的外径de、齿宽b.蜗轮的齿圈体积为:
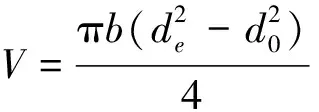
(1)
(2)
式(2)中,z2是蜗轮齿数;z1是蜗杆齿数;i是传动比,通常情况下是已知的;m是蜗轮模数;ψb是齿宽系数,按照蜗杆齿数不同,取0.75或0.67,通常情况下当z1=1~2时,ψb=0.75,当z1=3~6时,ψb=0.67;da1是蜗杆齿顶圆直径;q是直径系数;ψe是蜗轮齿圈外径系数;按照蜗杆齿数的不同,取2、1.5、1.
将式(2)代入(1)中,可以将体积公式转化为:
[(iz1+ψe+2)2-(iz1-4.4)2]
(3)
由式(3)可以看出,蜗轮齿圈体积与蜗杆头数z1,模数m,直径系数q有关,因此,选取蜗杆头数z1,模数m,直径系数q作为设计变量,即X=(x1,x2,x3)=(z1,m,q),所以式(3)可以改写为:
V=f(x)=
(ix1-4.4)2]
(4)
2.2 确定约束条件

(5)
2)蜗杆刚度的限制[4]。蜗杆工作时最大挠度不大于0.001d=0.001mq,即:

(6)
(3)蜗杆头数的限制。一般要求2≤z1≤3,因此有:
g3(x)=x1-3≤0
(7)
g4(x)=2-x1≤0
(8)
(4)模数的限制。对于中小功率得蜗杆传动,一般要求3≤m≤5,因此有
g5(x)=x2-5≤0
(9)
g6(x)=3-x2≤0
(10)
(5)蜗杆直径系数的限制。对于上述的模数范围,要求5≤q≤16,因此有:
g7(x)=x3-16≤0
(11)
g8(x)=5-x3≤0
(12)
由上述可以得到蜗杆传动的数学模型,式(4)是目标函数,式(5)到式(12)为约束条件,可见这是一个非线性约束优化问题,将本文提出的改进后的MIMIC算法应用在该模型中,进行求解。
3 优化结果分析
3.1 实验参数设置
在实验中,MIMIC算法的参数设置如下,群体规模N=200,截断选择S=N/2,保留的最优个体数p=20,最大迭代次数200,精度10-9,进行Rosenbrock法的初始点个数T=20,Rosenbrock法的初始步长δ=[1 1 1],增大系数α=3,收缩系数β=0.5,分别进行15次实验。
3.2 实验结果分析
表1 是经过MIMIC算法和Rb-MIMIC算法对模型进行优化后得到的结果,由表1可以看出,改进后的MIMIC算法,最优值和平均最优值明显都要小于MIMIC算法,而我们的实验结果希望金属圈体积尽可能的小,所以改进后的MIMIC算法要优于MIMIC算法,Rb-MIMIC算法在求精能力上有了显著的提高。而且Rb-MIMIC算法相比MIMIC算法进化代数也少了许多,说明Rb-MIMIC算法是一个可行的,求精能力强,收敛速度快的优化算法。
将MIMIC算法和Rb-MIMIC算法得到的优化结果进行圆整,经检验,圆整后的结果满足性能约束条件,将圆整后的结果与文献[3]中的结果进行比较,对比结果见表2.经过对比可以发现,MIMIC算法和Rb-MIMIC算法相对于常规优化设计,虽然蜗杆头数增加了,但是齿圈体积却大幅度减小,MIMIC算法和Rb-MIMIC算法优化后的齿圈体积减少了31%,但是Rb-MIMIC算法的进化代数明显小于MIMIC算法,充分显示了Rb-MIMIC算法的价值。
表1 MIMIC算法与Rb-MIMIC算法的比较
Tab.1 The comparison of MIMIC algorithm and Rb-MIMIC algorithm

算法最优值平均最优值蜗杆头数z1模数m直径系数q进化代数MIMIC602066.91604401.3833.923585231650Rb⁃MIMIC601777.35602949.63433.9229782915.999694827
表2 优化算法与常规设计对比结果
Tab.2 The results of optimization algorithm compared with conventional design

对比项蜗杆头数z1模数m直径系数q齿圈体积常规设计2518920226.4844MIMIC3416637934.1162Rb⁃MIMIC3416637934.1162
4 结 论
为了提高MIMIC算法的局部求精能力,收敛速度,本文在MIMIC算法的进化过程中加入局部求精能力强的Rosenbrock算法,利用Rosenbrock法随机搜索若干个体,将得到的新个体作为新群体的一部分,增加种群的多样性,从而使算法避免陷入早熟,使算法得到改进。
蜗杆传动是机械优化中一个广泛的应用,具有传动比大,传动平稳等优点,但是在设计中往往把蜗轮体积设计的比较大,造成有色贵重金属的浪费。如何在确保传动性能稳健可靠的前提下,使得蜗轮齿圈体积尽可能减小成为蜗杆传动的设计目标。本文将结合Rosenbrock算法的MIMIC算法应用在蜗杆蜗轮传动优化中。优化结果相比MIMIC算法和常规优化设计,体积显著减少,降低了制造成本,且改进后的MIMIC算法在收敛速度上也优于传统的MIMIC算法。优化结果表明改进后的MIMIC算法是一个有效的算法,求精能力强,收敛速度快,为蜗杆传动优化等约束优化问题提供了一种新的思路和方法。
参考文献:
[1] 孙全颖,王艺霖,杜须韦.遗传算法在机械优化设计中的应用[J].哈尔滨理工大学学报,2015,20(4):46-50.
[2] 苗君明.Matlab优化工具箱在蜗杆传动优化设计中的应用[J].沈阳航空航天大学学报,2011,28(4):60-62.
[3] 武洪恩,王宜宁,称玉玲,等.基于遗传算法的蜗杆蜗轮优化设计[J].制造业信息化,2015(3):20-23.
[4] 王远东.圆柱蜗杆传动的优化设计[J].机械传动,2016,40(2):162-164.
[5] DE BONET J S, ISBELL C L, VOILA P.MIMIC: Finding Optima by Estimating Probability Densities [J].Advances in Neural Information Processing Systems, 1997(9):424-430..
[6] 王圣尧,王凌,方晨,等.分布估计算法研究进展[J].控制与决策,2012,27(7):961-966.
[7] 龚纯,王正林.精通Matlab最优化计算[M].北京:电子工业出版社,2012.
[8] 张文林,夏桂梅.一种结合微粒群算法的混合MIMIC算法[J].太原科技大学学报,2015,36(5):406-410.
[9] 张金凤,夏桂梅,王泰.一种基于罚函数的混合分布估计算法[J].西南民族大学学报:自然科学版,2015,41(1):120-123.
[10] 顾灿春.普通圆柱蜗杆减速器的可靠性优化设计[J].电子机械工程,2003,19(3):44-47.
[11] 唐锦茹.蜗杆传动的优化设计[J].起重运输机械,1994(9):25-27.
