导流板对海底管线下沉自埋及涡振影响

姜文全, 姜昊君, 杨 帆, 张修铭, 邓子龙

(辽宁石油化工大学机械工程学院,辽宁抚顺 113001)

随着海底油气资源开采、运输技术的需求,油气集输领域的海底管线应用越发广泛。为保证海底管线免受复杂海底环境影响,将海底管线稳定地埋藏在海床之下显得尤为重要[1-4]。以至海底管线下沉、自埋、防振等防护技术研究日益增多[5-12]。其中,海底管线安装导流板作为一种有效防护措施的研究受国内外学者高度关注[13-14]。Hulsbergen、Bijker等[15-16]通过试验的方式研究了海底管线添加导流板后的冲刷效果,并得出在海底管线上方增设导流板可以增加海流对海床的冲刷深度和宽度,同时冲刷速度提高近10倍。Chiew等[17]针对海浪条件下导流板与海底管线受海流局部冲刷关系进行了试验研究。张芝永等[18]采用数值模拟与试验结合的方式研究了导流板对波浪环境下海底管线的影响,并提出导流板高度的增大能够使水平波浪力最大值随之增大,而垂直波浪力最大值则随之逐渐减小的变化规律。然而,在现有研究多为海底管线顶部竖直带有导流板,该结构极易使管线产生悬空状态下的涡流激振,影响其自埋及使用寿命等。笔者提出不同角度下的相切倾斜安装导流板的海底管线研究,探讨该形式导流板对管线下沉自埋及振动的影响。

1 数值计算

1.1 数值模型

应用ANSYS软件建立了海底管线流固耦合模型,湍流模型为k-ε模型[19]。海底管线直径为0.2 m,其中心线距离海底0.3 m,管线悬空跨度为1 m。模拟区域为三维流场网格分析模型,其尺寸为4 m×1 m×2 m,海流左端流入,边界条件为:u=0.1 m/s,v=w=0,由右端自由流出(图1)。流体区域模型下表面为海底固定壁面,上、前、后表面为对称面,管线与流体接触面为流固耦合面。

分别对无导流板海底管线、导流板与海水流向成30°、60°、90°夹角布置的海底管线进行模拟分析,得出4种不同情况的流场区域压力分布、流速分布云图、管线最大应力变化曲线、管线升力、拽力变化曲线及管线下沉变形量曲线(图2)。

图1 三维流场网格模型Fig.1 Grid model of three-dimensional flow field

图2 导流板布置Fig.2 Layout of spoilers

1.2 计算结果与试验结果验证

为验证海底管线流固耦合数值模拟结果的准确性,将未加装导流板的海底管线数值模拟的压力场、流场云图与现有试验结果进行对比分析,见图3。无导流板海底管线的压力场沿管线外表面分布:-30°至30°之间管线表面为正压,其余表面处于负压状态,且管线下表面高值负压区域大于上表面高值负压区域(图3(a))。如图3(b)所示,管前断面1流速自上而下分布为逐渐降低,管线最前端流速出现峰值,然后流速逐渐增加,但接近海床时流速锐减为0;管上断面2处流速自上而下逐渐增加,接近管线表面流速锐减为0;管后断面3流速自上而下逐渐减低,管线正后方流速为0,然后流速逐渐增加,接近海床附件流速迅速下降为0。综上分析可见,海底管线数值模拟的压力场、流场模拟结果与相关文献[20]中试验结果吻合较好。

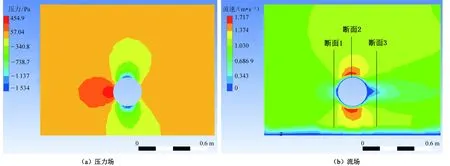
图3 海底管线周边压力场、流场数值模拟结果Fig.3 Numerical simulation results of pressure field and flow field around submarine pipeline

2 分析与讨论

2.1 导流板影响压力场

对海底管线压力场进行分析,得出导流板不同角度布置的压力云图(图4)。其中,图4(a)为未安装导流板管线,最大压力区域出现在管线来流方向正前方,最大压力为454.9 Pa,且管线上、下表面压力近似对称分布,上、下表面无压差;图4(b)为安装导流板与海水流动方向成30°夹角,管线附近最大压力区域出现在0°～40°,最大压力为474.8 Pa,且管线上、下表面压差为0.485 Pa;图4(c)为安装导流板与海水流动方向成60°夹角,管线附近最大压力区域出现在0°～90°,最大压力为490.4 Pa,且管线上、下表面压差为490.404 Pa;图4(d)为安装导流板与海水流动方向成90°夹角,管线附近最大压力区域出现在0°～90°,最大压力为493.5 Pa,且管线上、下表面压差为493.502 Pa。由此可知,海底管线上安装导流板,使得管线上、下表面压差海流区域形成压力差,有助于管线下沉自埋,压差随导流板的夹角增大而增大。但导流板安装管线正上方时,导流板和管线后侧将产生压力波动,将使管线产生涡激振动,不利于管线自埋。

图4 不同结构海底管线压力场云图Fig.4 Nephograms on pressure field of submarine pipelines with different structures

2.2 导流板影响流动特性

对海底管线流场进行分析,得出导流板不同角度布置的流场云图(图5)。图5(a)为未安装倒流板管线流场分布,此时管线上下两侧出现最大流速,其流速为1.717 m/s,流场呈对称分布,管线后侧未出现涡流现象;如图5(b)所示在管线上方安装导流板成30°时,流场对称分布现象消失,管线后方出现回流想象,最大流速出现在管线下方,其流速为1.953 m/s,海水对海床泥沙冲刷强度有所增加;图5(c)为导流板与流向成60°时,管线和导流板后方出现较大回流,并伴有轻度涡街现象,在管线下方最大流速增至2.574 m/s,海水加大冲刷海床强度,为管线下沉提供良好条件;图5(d)为导流板与流向成90°时,管线和导流板后方大面积区域形成流速波动区,使管线发生涡激振动,且管线下方最大流速降低为2.159 m/s,海水对海床冲刷强度减弱。综上分析可知,未加导流板管线自沉过程中受海床限制,很难实现自埋;而安装导流板后,海水对海床产生较大的冲刷力,为管线自埋创造条件。通过30°小倾角安装导流板、60°大倾角安装导流板和常规顶部(90°)安装导流板3种不同形式流场分析,60°大倾角安装导流板管线下方流速最大,冲刷形成的海床凹陷有利于管线下沉,其管线后方回流带起的泥沙对管线形成自埋。常规顶部安装导流板的海底管线,海床冲刷速度低于大倾角结构,且有管线涡激振动现象,不利于管线自埋。

2.3 管线受力变化

图6为模拟计算求得的管线所受升力、拽力变化。管道升力为负值,即海流对带有导流板海底管线产生的作用力竖直方向的分量方向向下,迫使管线下沉。由图6可知,导流板与水平60°夹角布置的管线所受升力绝对值最大,其数值为-550 N(即外径为200 mm、长为1 m的管线升力为-550 N)。在此升力和重力作用下,管线下沉变形。同时,管线所受的水平拽力也随导流板夹角增加呈现出上升趋势,但在夹角为60°处明显出现拐点。导流板与水平管线呈60°布置结构能够较好地改变海底管线受力状态,有利于管线下沉自埋。

图7为海底管线应力变化。由图7可以看出,装有导流板的海底管线中的应力呈波动变化,其平均应力随夹角的增加而增加。传统的90°夹角安装导流板的海底管线应力从0.18 MPa降到0.1 MPa,然后在0.11 MPa上下波动,且每个周期出现主、副两个峰值,使管线产生较强的振动变形。60°夹角安装导流板的海底管线应力峰值出现数量明显少于其他导流板安装方式的管线应力峰值数,同时该导流板-管线结构对其变形有较强的抑制作用,因此管线上未产生较为明显的振动现象。

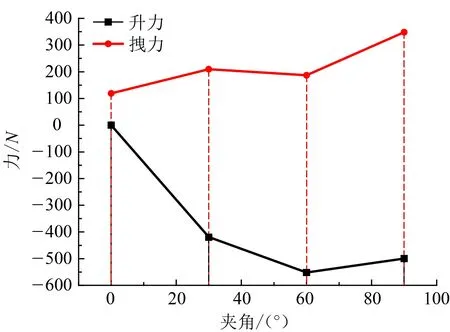
图6 海底管线升力、拽力曲线 Fig.6 Lift and pull curve of submarine pipeline

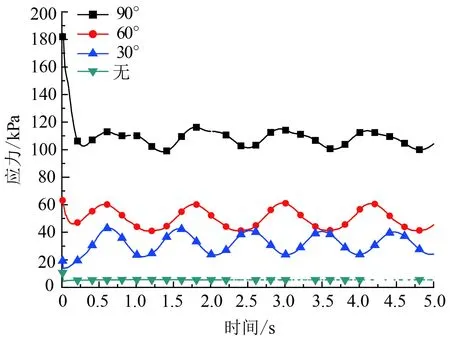
图7 海底管线应力变化曲线Fig.7 Stress change curve of submarine pipeline

2.4 管线下沉量变化

通过对海底管线进行流固耦合模拟计算,分别求得导流板与水平夹角90°、60°、30°及无导流板的海底管线下沉量曲线,如图8所示。由图8可见,海流冲击过程中海底管线的下沉量随导流板的夹角增大而增大,其中导流板垂直布置的管线受冲击变形量最大,达4.75×10-7m,0.5 s后下沉量恢复到1.85×10-7m,随后0.5～5.0 s内,管线下沉量在2.25×10-7m上下波动,且峰值逐渐衰减,体现出较强的振动现象发生。导流板夹角为60°的海底管线下沉量由2.63×10-7m恢复到1.24×10-7m,并趋于恒定。而导流板夹角为30°的海底管线下沉量由2.63×10-8m升高到7.52×10-8m后,波动变化,管线产生微幅振动。未安装导流板管线由自身重力所产生的下沉量只有8.01×10-9m。综上可见,传统的90°夹角安装导流板的海底管线虽然能够获得较大的下沉量,但管线整体处于振动状态,不利于管线自埋,同时振动也会带来一定的疲劳破坏隐患。而导流板与水平夹角60°安装于管线上,管线稳定下沉,达到管线自埋的目的。

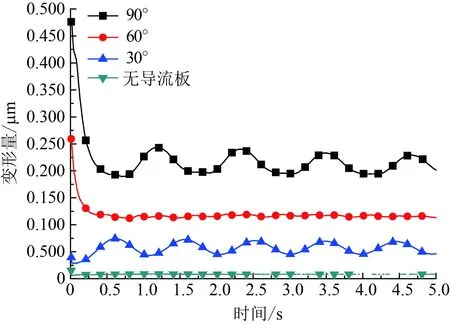
图8 海底管线下沉量变化曲线Fig.8 Change curve of submarine pipeline subsidence

3 结 论

(1)管线上、下表面的海流区域形成压力差,有助于管线下沉自埋,压力差随导流板的夹角增大而增大。管线正上方安装导流板时,导流板和管线后侧压力波动变化,使管线产生涡激振动现象,存在疲劳破坏隐患。

(2)大倾角60°安装导流板海底管线,其下方流速最大,冲刷海床形成凹陷为其下沉提供空间,管线后方回流带起的泥沙对管线形成自埋。

(3)得到导流板与水平夹角90°、60°、30°及无导流板等4种结构海底管线的升力、拽力变化及应力波动变化规律,60°夹角结构的下沉变形量出现趋恒现象。

参考文献:

[1] SHI Yumin, GAO Fuping. Lateral instability and tunnel erosion of a submarine pipeline: competition mechanism[J]. Bulletin of Engineering Geology and the Environment, 2017(7):1-12.

[2] HUANG Xiaoguang, XU Jinquan. Numerical procedure for static and dynamic analysis of fluid-conveying submarine pipeline span on linear elastic seabed[J]. Journal of Shanghai Jiaotong University (Science), 2010,15(6):719-725.

[3] WEN Shipeng, XU Jishang, HU Guanghai, et al. A field investigation on the effects of background erosion on the free span development of a submarine pipeline[J]. Journal of Ocean University of China, 2015, 14(4):621-628.

[4] GU Xiaoyun, GAO Fuping, PU Qun. Wave-soil-pipe coupling effect on submarine pipeline on-bottom stability[J]. Acta Mechanica Sinica, 2001,17(1):86-96.

[5] XU Jishang, LI Guangxue, JUAN J H, et al. Calculation of maximum allowable free span length and safety assessment of the DF1-1 submarine pipeline[J]. Journal of Ocean University of China, 2010,9(1):1-10.

[6] 王琳,李玉星,刘昶,等.考虑弹性基础的气液两相流海洋立管耦合振动分析[J].中国石油大学学报(自然科学版),2016,40(1):134-139.

WANG Lin, LI Yuxing, LIU Chang, et al. Fluid structure interaction analysis of gas-liquid two-phase flow in marine riser system on an elastic foundation[J]. Journal of China University of Petroleum (Edition of Natural Science),2016,40(1):134-139.

[7] LIANG Jing, YU Jianxing, YU Yang, et al. Energy transfer mechanism and probability analysis of submarine pipe laterally impacted by dropped objects[J]. China Ocean Engineering, 2016,30(3):319-328.

[8] LIU Run, WANG Wugang, YAN Shuwang. Finite element analysis on thermal upheaval buckling of submarine burial pipelines with initial imperfection[J]. Journal of Central South University, 2013,20(1): 236-245.

[9] SHA Y,WANG Y X,WANG G Y,et al. Experimental study on response of submarine pipeline over flat beds in steady flow[J]. New Trends in Fluid Mechanics Research, 2007(8):332-335.

[10] ENGIN G. Numerical analysis of deteriorated sub-sea pipelines under environmental loads[J]. Chinese Journal of Mechanical Engineering, 2015,28(6):1163-1170.

[11] MUHAMMAD S A, LI Cheng. A parallel three-dimensional scour model to predict flow and scour below a submarine pipeline[J]. Central European Journal of Physics, 2010,8(4):604-619.

[12] XU Jishang, PU Jinjing, LI Guangxue. Field observations of seabed scours around a submarine pipeline on cohesive bed[J]. 2012, 142:23-33.

[13] YANG Lipeng, SHI Bing, GUO Yakun,et al. Study on dynamic angle of repose for submarine pipeline with spoiler on sandy seabed[J]. Journal of Petroleum Exploration and Production Technology, 2012,2(4):229-236.

[14] HAN Yan, SHI Bing, REN Xingyue. Experimental study on the distribution of velocity and pressure near a submarine pipeline[J]. Journal of Ocean University of China, 2009,8(4):404-408.

[15] HULSBERGEN C H. Spoilers for stimulated self-Burial of submarine pipelines:Offshore Technology Conference, Houston, Texas, USA, May 5-8, 1986[C]. Texas：OnePetro, 1986.

[16] HULSBERGEN C H， BIJKER R． Effect of spoilers on submarine pipeline stability：Offshore Technology Conference，Houston，Texas，USA，May 1-4，1989[C] .Texas：OnePetro，1989.

[17] CHIEW Y M.Effect of spoilers on wave-induced scour at submarine pipelines[J].Journal of Waterway,Port,Costal and Ocean Engineering,1993,119(4):417-428.

[18] 张芝永,拾兵,阮雪景,等.导流板对波浪作用下海底管线影响研究[J].海洋工程,2012,30(4):90-96.

ZHANG Zhiyong, SHI Bing, RUAN Xuejing, et al. Study on the submarine pipeline with spoiler under wave action [J]. The Ocean Engineering, 2012,30(4):90-96.

[19] 王福军.计算流体动力学分析-CFD软件原理与应用[M].北京:清华大学出版社,2004.

[20] 王国兴.海底管线管跨结构涡致耦合振动的模拟与试验研究[D].青岛:中国海洋大学,2006.

WANG Guoxing. Numerical and experimental studies on vortex-induced vibrations with fluid-structure interaction for submarine free-span pipelines[D].Qingdao:Ocean University of China, 2006.