基于遗传算法的应急疏散中车辆路径规划研究

王逊，杜中军，刘孟轲，陈海祥

（四川大学计算机学院，成都 610065）

0 引言

随着现代城市发展与建设，人口越来越密集，如何在自然灾害、恐怖袭击等安全事件发生之后，快速有效地进行应急疏散，近年来成为交通规划与管理领域的一个新的研究方向。疏散路径规划是应急疏散的关键，车队运动问题（Convoy movement problem）是疏散路径规划中的一个重要子问题，在CMP中，给定一组车辆和一个用于机动的路网，每一辆车都有特定的起点和终点对，且有出发时间和到达时间的约束，如何高效规划每辆车的行驶路径是解决问题的焦点。

许多研究者将车队疏散问题抽象为网络流领域的问题来进行研究，Dunn和Newton提出了使用最大流方法来进行路径选择，Yamada运用最小代价流问题进行疏散交通分配，提出了最短路撤退规划（Shortest Evacuation Plan，SEP）方法。也有不少学者采用运筹学方法对其进行研究，Chardaire P等基于时间-空间网络的概念建立了针对CMP问题的整数规划模型，并通过拉格朗日松弛的方法对模型进行了求解，Gopalan R等系统研究了CMP问题的计算复杂度，并给出了针对其变式的多项式时间算法。Guan,L.提出了一种二阶段的方法，以车辆的效率最大化为标准为多任务指定车辆路径分配方法。Pinedo,Ruben D.研究了一个在不安全环境下，多起点、多终点的路径规划问题，为降低车辆的危险系数，给出了一种区域受限的救援车辆分配方法。

对于CMP及其衍生问题的研究，多优化两个方面的目标：一是缩短车辆道路机动时间，二是提高车辆的使用效率。然而，在应急疏散中，通过路径规划改进车辆组行驶的安全性能，同样是一个值得关注的问题，本文拟从这个角度，对多起点、多终点、多车辆的路径选择问题进行建模，并设计出一个基于优先级对染色体进行编码以建立路径树的遗传算法。

1 应急疏散中车辆路径规划建模

为突出车辆运动中的安全性问题，本模型对其他问题细节进行了合理的抽象和简化。第一、假设车辆的机动速度恒定不变，为某一常数；第二、假设每一路段都有明确的通行车辆上限；第三、假设在每一路段中，车辆的安全通行概率是确定的；第四、模型假设每一终点地最多只接收一辆车，这样能在一定程度上避免了车群的大规模损毁。

1.1 模型符号说明

模型中使用的角标说明：i表示起点地Oi，i=1,2，…，I，其中 I是起点地的数量；j表示终点地 Dj，j=1,2，…，J，其中J是终点地的数量；k表示k短路，对于每一个OD对，其中k=1,2,…,Kij,Kij是从起点地Oi到终点地Dj间待考虑的路径数量；l表示路段Al，l=1,2,…,L，其中L是所有OD对间的短路径中所有不重复的路段之和。

模型中使用的参数说明：wi表示从起点地Oi发出的车辆数；Pijk表示在从起点地Oi到终点地Dj间的第k短路可安全通行的概率；Rijk表示一个路段集合，包含从起点地Oi到终点地Dj间的第k短路中包含的所有路段；tl表示车辆通过路段Al所花费的时间，由路段长度和行驶速度计算得到；Te表示可用于车辆行驶的时间上限，应急疏散任务开始后，在该时间段内所有车辆必须完成行驶；αlijk为0–1变量，当从起点地Oi到终点地Dj间的第k短路中包含路段Al时取1，否则取0；λl表示路段Al的车辆通行上限。

模型中的决策变量：xijk为0-1变量，当存在一辆车从起点地Oi向终点地Dj经由该OD对间的第k短路机动时取1，没有车经过该路径时取0。

1.2 模型构建及解释

模型旨在对路网中车辆行驶路径选择的安全性问题进行优化。

公式（1）是模型的目标函数，它表示最大化各车辆安全完成行驶任务的概率之和。公式（2）表示从起点地发出的车必须被制定一条路径和一个可用的终点地；公式（3）对应假设四，表示每一终点地最多接收一辆车；公式（4）指出每一辆车进行路径选择时必须满足任务时间限制；公式（5）表示从Oi到Dj间的第k短路径的安全通行概率为该路径内各个路段安全通行概率之乘积；公式（6）表示在整个行驶过程中，各个路段中通行的车辆总数小于或等于该路段的通行上限。

2 基于遗传算法的模型求解过程

模型的遗传算法借鉴Altiparmak Fulya给出的一种基于优先权的编码方法，每一个基因位表示一个起点或终点，基因位上的值表示对应点在构建路径树时的优先权，数值越大，优先权越高，这类方法将不同染色体解码为同一路径树的概率极低，性能也非常稳定。

2.1 编码设计

模型中染色体长度为I+J位，其中I为起点地数量，J为终点地数量，前I个基因代表I个起点地，后J个基因代表J个终点地，每一位基因上表征一个数字，代表该起点或者终点地的优先权。同时，生成一个辅助算子与染色体长度相同，同为I+J位，辅助算子上每一位表征一个数字，代表该起点地或者终点地还可以发车或者接车的数量，如图1所示，染色体中前三位基因表示三个起点地，优先权分别为4、1、8，后五位基因表示五个终点地，优先权分别为 5、2、6、3、7，辅助算子中前三位分别表示三个起点地要发出车辆的数量分别为1、1、2，后五位分别表示五个终点地可以接车的数量，均为1。

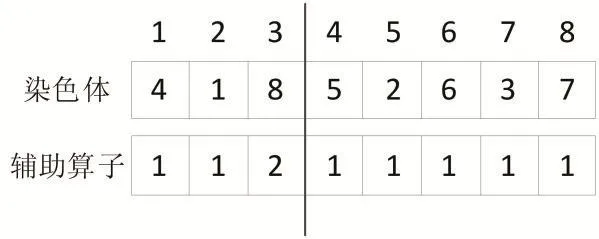
图1 染色体与辅助算子实例

2.2 遗传操作

遗传操作中，主要有选择、交叉和变异三个阶段。

在选择阶段，需要对候选染色体进行解码，每一染色体解码后会生成一套车辆路径规划方案，带入目标函数，可以计算出该方案获得车辆的总安全通信概率，将此作为该染色体的适应度，从而进行遗传选择。一般而言，设置固定选择比例，适应度较优的染色体保留，适应度较差的染色体进行交叉或变异阶段。

在交叉阶段，在两个父代染色体中随机选取两个位置，两个父代染色体中两个位置之间的基因段定义为映射区，将两映射区的基因进行互换，互换后会出现同一染色体中出现基因位优先权数字一样的情况，在保持互换的基因段和非重合基因不变的情况下，将重复的基因进行冲突消除，这样就可以交叉得到两条没有冲突的子代染色体。

在变异阶段，随机选择变异染色体，然后在待变染色体上随机选择两个位置，将这两个位置的基因进行互换，变可得到变异后的新染色体。

2.3 解码设计

解码的过程就是一个逐渐生成车辆规划路径的过程，先给染色体中优先权最高的基因进行路径选择，优先权最高的路径选择完毕后更新优先权，再给优先权最高的基因进行路径选择，直到所有车辆都已经完成路径选择，则完成了该染色体解码。在路径选择中，一般采用贪婪算法，即为优先权最高的基因分配最佳的行驶路径，只要该路径满足其他约束条件，例如时间的约束、资源的约束和最大通行量的约束等。

本模型染色体的解码流程如下：

输入：染色体和辅助算子。

输出：车辆行驶路径树。

Step1:选择染色体中优先权最高的基因，使用贪婪算法，为该基因选择一条最佳路径；

Step2:若选择成功，则将该路径加入路径树，同时，将该路径的起点和终点基因位上辅助算子的数字减1；

Step3:若选择失败，则标记该染色体无效，退出解码。

Step4:辅助算子中数字为0的位置，将染色体中该位置的优先权数字变为0；

Step5:若染色体中前I位基因或者后J位基因均为0，则停止解码，输出路径树，否则，继续Step1。

2.4 求解过程

模型中目标函数多为概率值构成，且数值均较小，为突出各染色体的性能各异，可将概率值取负对数处理，由此将模型的目标函数转为：

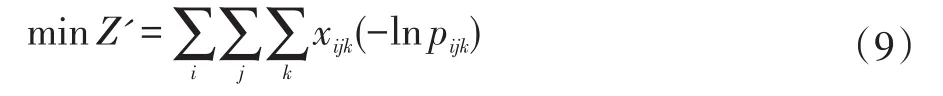
相应的，约束条件（5）也转化为：

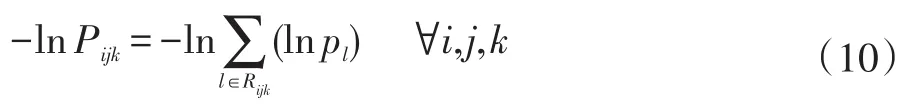
在遗传算法中进行最佳路径的选择，需要先使用A*算法对路径进行预处理计算，求得每一个起点地与每一个终点地的k最短路径，以备遗传算法中进行路径选择。

由此，求解过程如下：

Step1：使用A*算法生成所有起点地和终点地对的k最短路径；

Step2：初始化染色体和辅助算子种群；

Step3：计算染色体适应度，迭代进行选择、交叉、变异操作；

Step4：迭代过程中国，持续N代未出现更优解，则停止计算，输出结果。

3 实验案例

3.1 实验环境

本实验的运行环境是，64位Windows 7操作系统，Intel Core i7 3.6GHz处理器和12GB的内存，其实现平台为MATLAB软件。实验对象为系统随机生成的10个不同大小规模的车辆行驶路网，其中实验参数设置为，每一路段的最大通行量为5，各路段的安全通行概率，通行时间等参数为随机生成。遗传算法中的选择概率为0.85，交叉概率为0.85，变异概率为0.15，持续10代未出现更优解，则停止计算。

3.2 实验结果

随机生成10个不同大小规模的车辆行驶路网，其具体情况如表1所示。

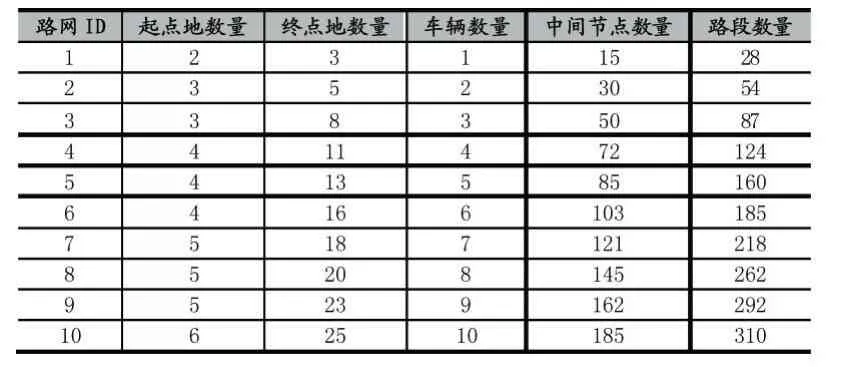
表1 10个不同规模的路径网络情况

经过建模及求解过程，可得车辆路径规划结果，其中选取路网6中的车辆路径规划结果如表2所示。

表2 路网6中遗传算法计算出的最优车辆行驶方案

在不同路网中进行实验，遗传算法对解的性能提升率如表3所示。

表3 各路网中遗传算法的性能提升情况

3.3 结果分析

在10个规模大小不同的路网中进行实验，根据表3.3可以分析得出，对于小规模路径规划，遗传算法的性能提升并不太大，因为其初始解中可能就已经包括了优化解，而随着问题的规模变大，遗传算法的逐步得到体现，在路网7和路网9中，性能提升率均超过了300%，同时由于遗传算法的收敛性，本实验均在有效时间内完成了计算。

4 结语

源和通行限制等外部约束，为了有效地对模型进行求解，引入遗传算法，针对车辆路径规划问题，提出了基于优先权的染色体设计和等长辅助算子的设计，使得遗传算法能更好地适用于本问题，最后通过对10个不同规模大小的路径规划问题进行实验，验证了本文提出的模型及遗传算法求解的有效性。当然，该问题并未彻底解决，本文中提出的算法也存在随着车辆的数量、起点地的数量和终点地的数量增加，运算时间会大幅增长，原因在于解码的效率问题，这也是笔者下一步要研究的方向。

本文首先对应急疏散中车辆路径规划问题进行了建模，其目标旨在车辆的安全性，综合考虑了时间、资

参考文献：

[1]Yamada T.A Network Flow Approach to a City Emergency Evacuation Planning[J].International Journal of Systems Science，1996,27（10）:931-936.

[2]Chardaire P,Richardson S B.Solving a Time-Space Network Formulation for the Convoy Movement Problem[J].Operations Research,2005,53（2）:219-230.

[3]Gopalan R.Computational Complexity of Convoy Movement Planning Problems[J].Mathematical Methods of Operations Research,2015,82（1）:31-60.

[4]Guan L.The Research of The Optimal Distribution for the Multitask using Types of Vehicles[C].International Conference on Transportation Engineer 2007.ASCE,2015:539-544.

[5]Pinedo Y,Ruben D.Route Optimization While Improving Safety Using Escort Vehicles[J].Dissertations&Theses-Gradworks，2013.

[6]陈华华,杜歆,顾伟康.基于遗传算法的静态环境全局路径规划[J].浙江大学学报，2015,32（1）:49-53.

[7]马超,郭健,阚映红,王卉,唐金龙.基于遗传算法的应急疏散方案研究[J].测绘科学学报，2013，29（6）.

[8]Aljazzar H,Leue S.K:A Heuristic Search Algorithm for Find The K-shortest Paths[J].Artificial Intelligence,2011,175（18）:2129-2154.