一类SIR和SIS组合的复杂金融网络风险传染模型稳定性分析

刘晓宇 吕 琳

（哈尔滨金融学院，黑龙江 哈尔滨 150030）

引言

网络理论是数学理论的一个分支，具有拓扑性质。如果网络中存在多主体节点，且可以演化成为多种不同的网络结构，这种网络称为复杂网络。网络可以准确描述金融市场之间复杂关系，网络中所有节点通过各种金融关联相互连接起来，这种金融关联直接反映金融各个节点之间的风险。基于复杂网络的金融风险分析能够研究不同风险蔓延，可以清晰地分析金融市场风险蔓延趋势，直接而形象地刻画出金融系统内在联系，并在此基础上分析金融市场之间的互动与关联。由于复杂网络在描述市场间的关联结构和投资者间交互作用具有明显优势，越来越多的学者将其引入金融领域研究风险传染问题。Allen等研究银行间市场风险传染问题[1]。May等认为传染病的传播和金融风险的传染非常相似，Garas等将传染系统动力学SIR传染模型应用于金融危机在世界各国间扩散的研究，说明金融风险研究进入新阶段[2-3]。Allen等认为不完全市场结构造就易感群体，发现市场结构越完全，风险越容易阻断传染[4]；Gao运用复杂网络系统工程理论构建银行网络SIR模型，得到风险传染阈值[5]。Demiris等运用贝叶斯估计方法研究金融危机扩散SIR模型，考虑国家金融联系和贸易联系，发现推行降低金融系统脆弱性政策有助于减缓危机的扩散[6]。Toivanen构建银行间同业市场风险传染SIR模型，将传染概率设定为离散的比值[7]。李守伟借助传染病思想建立银行风险传染的随机模型，发现增加治理率和降低关联度可以有效减少风险的传染[8]。马源源运用SIR模型模拟股市危机扩散过程，给出股市危机扩散模型计算方法[9]。鉴于此，本文将传染病动力学和复杂网络理论有机结合，建立一类SIR和SIS组合的金融市场风险传染系统动力学模型，分析模型平衡点存在性和稳定性，确定金融风险传染阈值R0。

一、模型建立

（一）研究假设

金融系统中不同市场抗风险能力不同，各个子市场被风险传染后，其中部分节点子市场能够通过有效防范对策对风险永久免疫；恢复为风险免疫子市场，另一部分节点子市场在被风险传染后，没有及时有效控制，因而无法形成对风险的免疫，再次进入风险暴露子市场。

（二）模型构建

借助于传染病模型[10-11]构建一类SIR和SIS组合的金融市场风险传染系统动力学模型，变量和参数设定如下：

在金融网络中将网络节点为三个类别，即S（t），I（t），R（t）。

S（t）为风险暴露子市场，表示t时刻尚未被传染，但缺乏风险防御能力且容易被传染风险的子市场节点数量，在风险传染中起到主导作用；

I（t）为风险感染子市场，表示t时刻已被风险传染的且可将风险传染给其他子市场节点数量；

R（t）为风险免疫子市场，表示t时刻在金融市场风险传染过程中具有免疫能力的子市场节点数量；

N（t）表示t时刻金融网络各子市场节点的总量，A表示单位时间内各子市场节点增加的数量；d表示子市场退出率；由于各个子市场的参与主体、业务类型和监管规则等存在差异，各类子市场抗风险能力不同。设在单位时间内由I（t）子市场进入S（t）子市场节点的数量在I（t）子市场节点中所占比例为c，称为无免疫易感率。r表示移出率，也称风险管理系数，β表示各个节点子市场之间风险传染概率，风险暴露子市场与其他子市场的接触率为f（S），由于风险只能传染给风险暴露的子市场，故有效接触率为βf（S），为非线性传染率，因此t时刻新增风险传染的子市场数量为βf（S）I（t），假设A，d，α，r，β均是正常数。由此建立一类SIR和SIS组合复杂金融网络风险传染模型：

由模型可得t时刻S（t），I（t），R（t）子市场节点数量满足的微分方程为：

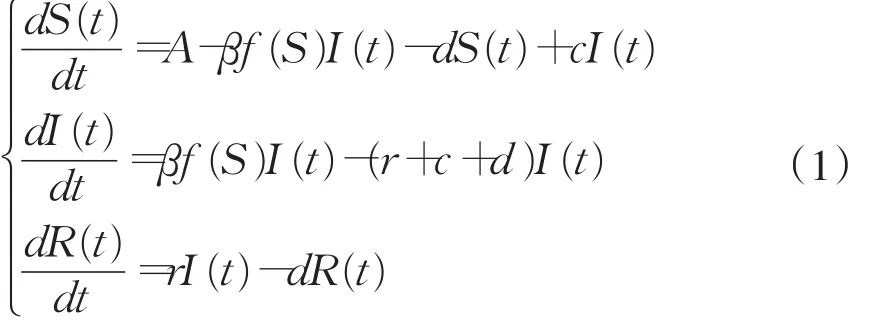
模型（1）的基本假设

①f（S）满足在S≥0上是一个非负不减连续函数，且f（0）=0。在S≥0上连续可微，f'（S）＞0；

②基于模型（1）的金融学意义，S（t），I（t），R（t）均为非负。

将模型（1）的三个方程相加可得出金融网络各子市场节点总数量N（t）满足方程：

由比较原理可知 ∃T＞0，当t＞T时，N（t）≤A/d。因此从模型（1）出发的解将最终进入或停留在D⊂R3+

其 中D={（S（t），I（t），R（t））∈R3+|0 ≤S（t）+I（t）+R（t）≤A/d，S（t），I（t），R（t）≥0}

D是模型（1）的正向最大不变集[12]。

二、模型平衡点的存在性和稳定性分析

（一）平衡点的存在性分析

模型（1）的前两个方程不含R，所以可从前两个方程研究S，I的性态，若要了解R的性态可再由模型（1）第三个方程讨论。

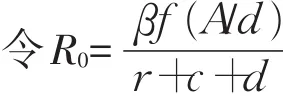
性质1模型（3）总有非零平衡点（A/d，0，0）；当R0＞1且A＞dS*时，模型（3）除存在无风险平衡点P0外，还存在非零风险平衡点P*（S*，I*）。

（3）有唯一正平衡点，由（3）求得模型（3）的平衡点应满足下列关系式：

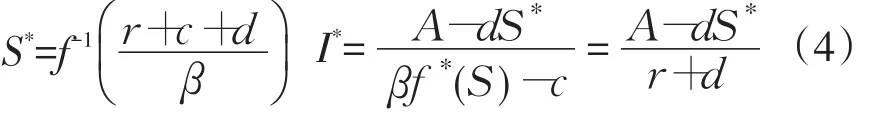
（二）无风险平衡点P0的稳定性分析

性质2 当R0≤1时，模型（3）无风险平衡点P0全局渐近稳定；当R0＞1时，P0不稳定。

证明：考虑Liapunov函数V（t）=I（t）

将V（t）关于模型（3）对t求导

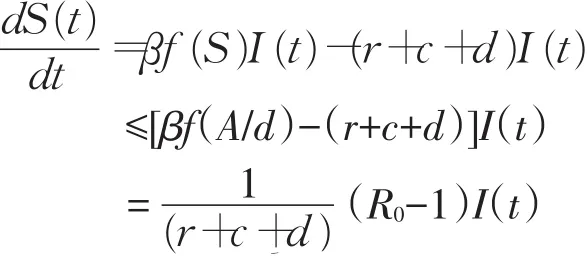
（三）非零风险平衡点P*的稳定性分析

性质3 当R0＞1且A＞dS*时，模型（3）的非零风险平衡点P*全局渐近稳定。

证明：考虑Liapunov函数

其中g（x）=βf（S）-（d+c+r），由模型的基本假设可知g（x）是单调递增函数，且f（S*）=0，c1，c2是正常数，故V（S（t），I（t））≥0当且仅当S=S*，I=I*时V（S（t），I（t））-0。

将V关于模型（3）对t求导

因为c2＞0（βf（S*））＞c，

由（3）式的第二个方程可知：

又因为

所以

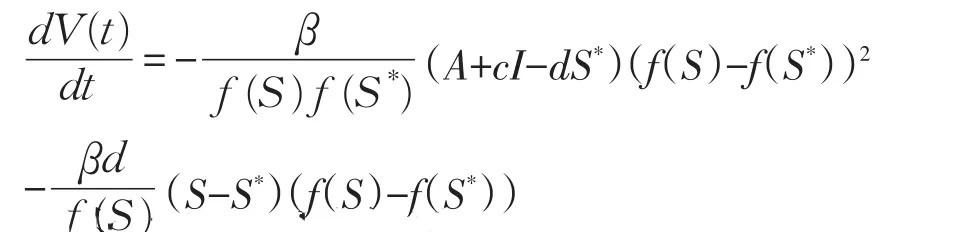
三、结论

四、控制金融风险的对策建议

（一）构建健全风险预警机制和管控机制

构建风险预警机制，需要选取能够反映金融市场风险影响的内外部潜在因素指标，构建高度关联的子市场风险监测指标体系，根据指标变动情况识别风险。目前，数字经济带来新的风险，应更新风险管理工具，利用金融工程方法、人工智能技术、机器学习算法和统计分析方法建立新型风险预警模型。当金融市场外部环境发生改变，会改变风险的发生概率和损失程度，引起指标变动即可预警风险。除构建风险预警机制，防范金融风险的第一道防线是金融市场内部风险管控机制。一般来说，短期内金融市场风险容易隐藏，但中长期来看，积累金融风险会越来越大，蔓延整个金融体系，以短期内金融市场风险防控非常重要，但目前我国防范及控制金融风险时却忽略了这一点。因此，对各类子市场实时监测预警，对预警机制实行管理，同时对金融市场中异常交易重点监测，可有效预防风险发生和恶化，缩小风险传染范围。

（二）建立有效的风险隔离机制

一些子市场关联度较高，即模型（1）中的βf（S）较大，当一类子市场感染风险后会立即传染给其他子市场。因此，当个别子市场感染风险后，要建立有效的风险隔离机制，防止风险进一步蔓延和传递，风险隔离机制可有效地控制风险引起的连锁反应，降低各类子市场之间的风险传染概率，从总体上减少风险造成的损失程度。要重视识别可影响金融主体的潜在风险，管理风险以使其在该主体的风险偏好之内，并为主体目标的实现提供合理保证。此外，还可考虑将风险隔离机制逐级延伸覆盖至乡镇、街道乃至社区、村委，建立多层次的金融风险隔离机制，在全国率先实现金融风险防控全覆盖。

（三）优化金融监管体系

金融监管是防范和化解金融风险的必要条件，模型（1）风险管理系数r主要与子市场风险防范和金融监管部门监管力度相关。监管部门力度越大，越有利于风险防控。监管目的是防范金融风险，同时兼顾培育金融市场，鼓励金融创新和制度创新，监管部门通过建立健全监管制度，优化金融监管体系，监督金融机构的经营活动，降低和控制金融体系风险。金融监管体系构建，要结合金融发展的实际。目前互联网金融在金融体系中发挥着越来越重要的作用，各种互联网+金融已经遍布金融领域，优化金融监管体系，要结合目前金融风险新特点。我国目前尚无风险管理的创新经验，可选择与互联网金融风险防范能力较强的国家和机构合作，优化金融监管体系，促进金融市场健康有序发展。除此之外，优化金融监管体系要利用网络技术，按照匹配性、全覆盖、独立性和有效性原则，建立健全全面风险管理体系，加强金融市场外部监管。利用网络技术对金融市场的各类参与者及其融资、交易活动及对市场运行的组织、协调和监督措施等全面监管。同时通过金融风险监管体系，对各类金融风险，强化功能监管，协同分业监管。

（四）完善金融法制法规

随着网络技术的普及及发展，金融风险呈现隐蔽性、复杂性及扩散性特点，除有效预警机制、风险隔离机制以及金融监管体系，还需要与之配套的金融法制法规规避和管理金融风险。首先，细化金融监管机构的法律责任，金融监管机构的考核内容和责任要更加细化，明确规定相应处罚奖励措施。其次，完善金融监管法律，随着经济的发展，金融创新层出不穷，但与之配套的相关监管法律法规相对滞后。此外，金融机构内部也应建立完善的风险规避制度。从内部控制入手，建立相应制度独立负责金融风险预防和控制，及时发现风险并加以防范。

参考文献：

［1］ Allen F,Babus A.Networks in France.In Kleindorfer P R,Wind Y.edc.The Netword Challenge：Strategy,Profit,and Risk in an Interlinked Word[J].Harvard Bussiness Review,2009(9).

［2］ May R M,Levin S A,Sugihara G.Complex Systems：Ecology for Bankers[J].Nature,2008(51).

［3］Garas A P,Argyrakis C,Rozenblat M,et al.Worldwide Spreading of Economic Crisis[J].New Journal of Physics,2010(11).

［4］ Allen Gale.Financial Contagion[J].Jouranl of Political Economy,2000(1).

［5］ Cao H H,Zhu J M.Research on Banking Crisis Contagion Dynamics Based on the Complex Network of System Engineering[J].Systems Engineering Proce-dia,2012(5).

［6］ Demiris N,Kypraios T,Smith L V.On the Epidemic of Financial Crises,Centre for Financial Analysis and Policy[J].Working Paper,2013,43.

［7］Toivanen M.Contagion in the Interbank Net-work：An Epidemiological Approach,Bank of Finland Research[J].Discussion Paper,2013(19).

［8］李守伟,何建敏.基于复杂网络的银行同业拆借市场稳定性研究[J].管理工程学报,2011(2).

［9］马源源,庄新田.股市中危机传播的SIR模型及其仿真[J].管理科学学报,2013(7).

［10］马知恩,周义仓.传染病动力学数学建模与研究[M].北京：科学出版社,2004.

［11］樊志良,张菊平.一类具有常数移民的SIR和SIS组合流行病模型[J].华北工学院学报,2004(2).

［12］Freedom H I,Tang M X,Ruan S G.Uniform Persistence and Flows Near a Closed Positively Invariant Set[J].Dynam Diff Equat,1994(4).

［13］廖晓昕.稳定性的理论、方法和应用[M].武汉：华中理工大学出版社,1999.