基于网状静电传感器鼓泡流化床运行参数监测

张文彪，杨彬彬，程旭峰

基于网状静电传感器鼓泡流化床运行参数监测

张文彪，杨彬彬，程旭峰

(华北电力大学 控制与计算机工程学院，北京，102206)

为了深入研究流化床中颗粒的流动特性和优化流化床反应器的性能，需要对流化床的运行参数如流速和电荷分布进行实时地监测。由于灵敏度高且分布均匀，网状静电传感器被用来在实验室规模鼓泡流化床上测量固体颗粒的速度廓形和电荷分布。固体颗粒的速度廓形是通过对上下游平面对应位置的静电信号进行互相关计算得到的。网状电极上的感应电荷可以通过静电信号的均方根(RMS)估算。根据电荷重建算法，利用所有电极上的感应电荷重建截面处固体颗粒的电荷分布。研究结果表明：网状静电传感器可以捕捉到鼓泡流化床床壁附近的下落颗粒；由于流化床内颗粒速度廓形的影响，传感器中心处电极上的感应电荷量大于床壁附近电极上的感应电荷量，并且重建结果显示流化床截面电荷分布相对均匀。

网状静电传感器；鼓泡流化床；电荷分布；速度廓形

流化床由于具有优良的传热与传质效率和处理大量颗粒的能力，已经被广泛应用于石油、化工、电力和冶金等工业场合。流化床中颗粒的流动特性对流化床的性能和产品质量有着至关重要的影响。目前，国际上有很多关于流化床中颗粒流动参数的测量方法。SHAFFER等[1]利用高速摄像法对循环流化床上升段中颗粒的流动特性进行了研究。LAVERMAN等[2]使用粒子图像测速仪(PIV)并结合数字图像算法测量了二维流化床中颗粒相的速度分布，气泡直径和气泡速度等。MUELLER等[3]将磁共振成像技术(MRI)应用于分析流化床中颗粒的运动特性。放射性粒子跟踪(RPT)技术和正电子发射粒子跟踪(PEPT)技术也被用于追踪颗粒在流化床中的运动轨迹[4−5]。然而，上述这些方法大都由于成本较高和测量装置复杂等缺点，难以推广应用于恶劣的工业场合。静电测量技术是近年来新兴的一种测量气固两相流流动参数的方法，该方法具有结构简单、灵敏度高、成本较低和性能稳定且适合应用于恶劣的工况环境等优点。静电传感器目前已经成功用于气力输送过程中[6−8]。近年来，静电传感器也被尝试用于测量流化床内固体颗粒的流动特性。ZHANG等[9]使用静电传感器和电容层析成像技术研究了三床循环流化床中颗粒流动的动力学特性。ZHANG等[10]还利用弧形静电传感器阵列测量了鼓泡流化床中固体颗粒的流动参数。然而，环形和弧形静电传感器由于受灵敏度分布特性的影响，很难清楚描述流化床整个截面不同径向位置处固体颗粒的流动特性。由于固体颗粒与空气相对运动，颗粒与颗粒之间的摩擦以及颗粒与床壁碰撞，颗粒会带上电荷。如果这种静电现象不能得到实时地监测和控制，将会导致颗粒团聚和颗粒粘附在床壁，会影响流化床的运行，甚至引起静电放电和爆炸等事故。现有颗粒电荷的测量方法主要包括法拉第桶法[11−12]、静电成像法[13−14]和静电电极 法[15−17]等。法拉第桶测量颗粒的带电量时需要对颗粒进行采样，采样过程会使颗粒发生额外的电荷生成或耗散，使测量结果出现误差。对于静电成像法，由于传感器灵敏度分布不均匀，重建后的电荷分布可能无法代表真实的电荷分布。静电电极法已被广泛用于测量流化床中的电荷分布。CHEN等[15]利用非侵入式电极重建了二维床气泡周围固体颗粒的电荷分布情况。HE等[16−17]利用双尖端静电电极研究了气固流化床中的气泡特性和电荷分布，得到的颗粒电荷密度和气泡上升速度与法拉第桶和高速相机所得结果很接近。SUN等[18−19]利用弧形静电电极研究了循环流化床内的流场间歇性和相干性，并利用静电脉动信号对颗粒团聚现象进行了表征。然而，静电电极只对电极附近的颗粒敏感，并且流化床内流动情况十分复杂，少数几点的测量结果很难代表整个截面处的电荷分布。针对上面提到的问题，本文作者提出一种网状静电传感器用于鼓泡流化床整个截面的电荷分布和颗粒流动特性的测量。相比于上述提到的各类静电传感器，网状静电传感器可得到更高和更加均匀的空间灵敏度分布，尤其适用于大管径复杂流场的测量[20]。但是，网状静电传感器的缺点是在测量过程中网状电极会对流场造成一定程度阻碍，会导致电极磨损和干扰流场的问题。为了解决以上问题，耐磨材料被用于降低电极的磨损程度，并且通过合理布置电极数量，可以在低阻碍程度下使灵敏度均匀分布。

1 网状静电传感器

基于静电感应原理的网状静电传感器其几何结构见图1。网状传感器的电极由两组直径为1.5 mm的绝缘导线互相垂直构成。综合考虑传感器灵敏度分布的均匀性和对流场的阻碍作用，每组电极包括8根间距为20 mm的导线，组成8×8的网状结构。考虑到电极的耐磨性和强度要求，电极内部由直径为1 mm的不锈钢丝组成。不锈钢丝外部包裹着厚度为0.25 mm的热缩管，可以防止颗粒与电极接触时发生直接电荷转移。对于当前传感器结构，网状电极的阻挡面积大约为总面积的14%，通过减少导线的数量以及增大导线之间的间距的降低电极对流场的阻碍程度。在鼓泡流化床中，网状传感器分布在上、下2个测量平面。上游电极平面被安装在距离鼓泡床底部240 mm的位置，上、下游电极平面之间的距离为20 mm。图1中还给出了上、下游网状电极的分布情况，上游电极1到电极8与下游电极17到电极24一一对应，上游电极9到电极16与下游电极25到电极32一一对应。

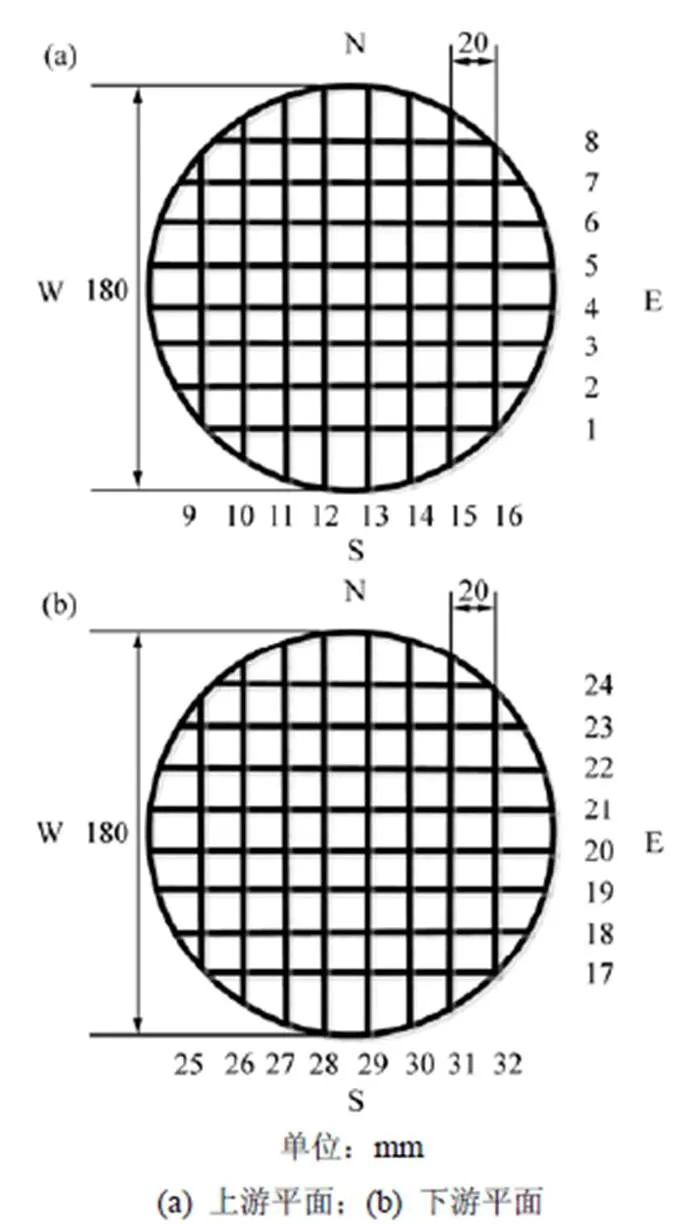
图1 网状电极的几何结构及电极分布

网状静电传感器的测量原理如图2所示。当带电颗粒通过上、下游网状电极时，上、下游对应位置的电极根据静电感应原理会依次生成感应电荷，感应电荷的波动产生感应电流。信号调理电路将微弱的电流信号转换成电压信号。为了获得更高的信噪比，一般将信号调理电路置于电极附近。通过电流/电压转换、放大和滤波，便可以得到上下游网状电极上的静电信号。上、下游网状电极所得的静电信号通过数据采集卡被同步地记录和储存，采样频率为2 000 Hz，采样长度为600 000个数据。通过对上、下游对应位置电极所得静电信号进行互相关计算，可以得出流化床内颗粒的轴向速度分布。通过计算每个电极上的感应电荷，并且结合电荷分布重建算法可以得出流化床截面处的电荷分布情况。

由于网状电极是插入流化床中的，流化床中的静电放电现象会使所静电信号出现尖峰脉冲。虽然信号调理电路对尖峰脉冲有一定的抑制作用，但是所得静电信号中仍然存在尖峰，如图3(a)所示。由于这种尖峰脉冲会造成后续信号处理出现错误，本文使用小波滤波算法降低这种干扰的影响。滤波过程中使用的小波基为db4，分解的层数为3层，并且使用软阈值算法滤除干扰。图3(b)所示为经过滤波之后的信号波形，从该波形中可看出该方法可以很好去除静电信号中的噪声和尖峰脉冲。

图2 网状静电传感器测量原理

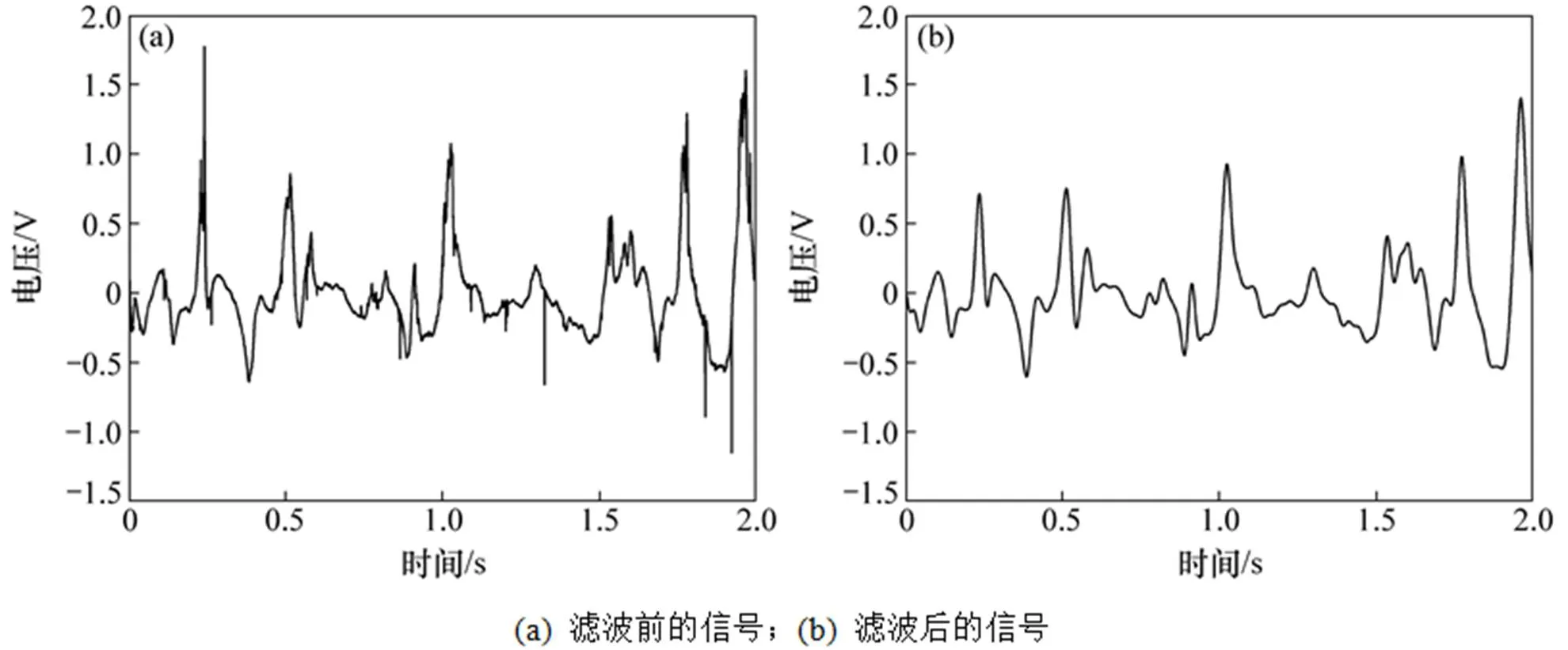
图3 小波滤波前后的静电感应信号

2 实验装置

鼓泡流化床实验装置如图4所示，实验平台主要包括风机、缓冲罐、气体流量计和鼓泡床等。流化床的材料为有机玻璃，内径为180 mm，厚度为5 mm，高度为2 m。从风机中得到的流化气体通过布风板进入床层，并带动固体颗粒运动形成鼓泡流化状态。在实验过程中，流化气体的温度为18℃，相对湿度为27%。实验中使用的固体颗粒为石英砂，颗粒的粒径范围为150~200 µm，真实密度为2.56 g/cm3。固体颗粒在使用前要进行干燥，以去除颗粒湿度的影响。实验前颗粒静止床高为345 mm，并且通过长时间的流化使颗粒达到带电饱和状态。在实验过程中，通过玻璃转子流量计测量气体流量，气体流量分别设置为2.4，3.6，5.0和7.0 m3/h。

图4 鼓泡流化床实验装置

3 实验结果与讨论

3.1 互相关计算

在理想条件下，上、下游电极采集到的静电信号在形状上是相似的，仅仅在时间上存在一定的迟延。通过对上、下游静电信号进行互相关计算。相关函数的峰值为相关系数，相关系数是上、下游信号相似程度的参数，可以表征流体流动的稳定性。利用峰值对应的延迟时间可以计算出相关速度，相关速度可以看作对应位置上固体颗粒的轴向速度。图5所示为不同气体流量条件下，互相关系数在流化床截面处的分布。图中电极在流化截面处的位置被转换成了归一化坐标。从图5可以看出：随着流化气体流量增加，互相关系数变低。这是由于气速增加，气泡的运动变得更加复杂和不稳定，因此，固体颗粒的流动变得更加剧烈，上、下游静电信号的相似程度降低。并且由于流化气体在流化床截面分布相对均匀，沿着径向方向互相关系数相差不大。

图6所示为气体流量为7.0 m3/h时，流化床中心处与床壁附近的相关速度。由于气泡在上升的过程中会变得越来越大，最后由于过大失稳而在床层表面破裂，气泡夹带的颗粒被抛向床壁附近，由于重力影响而下落，因此，在床壁附近发现有下落颗粒。图6表明床壁附近的电极会出现负的相关速度，说明利用网状电极可以捕捉到颗粒在床壁处的下落现象。

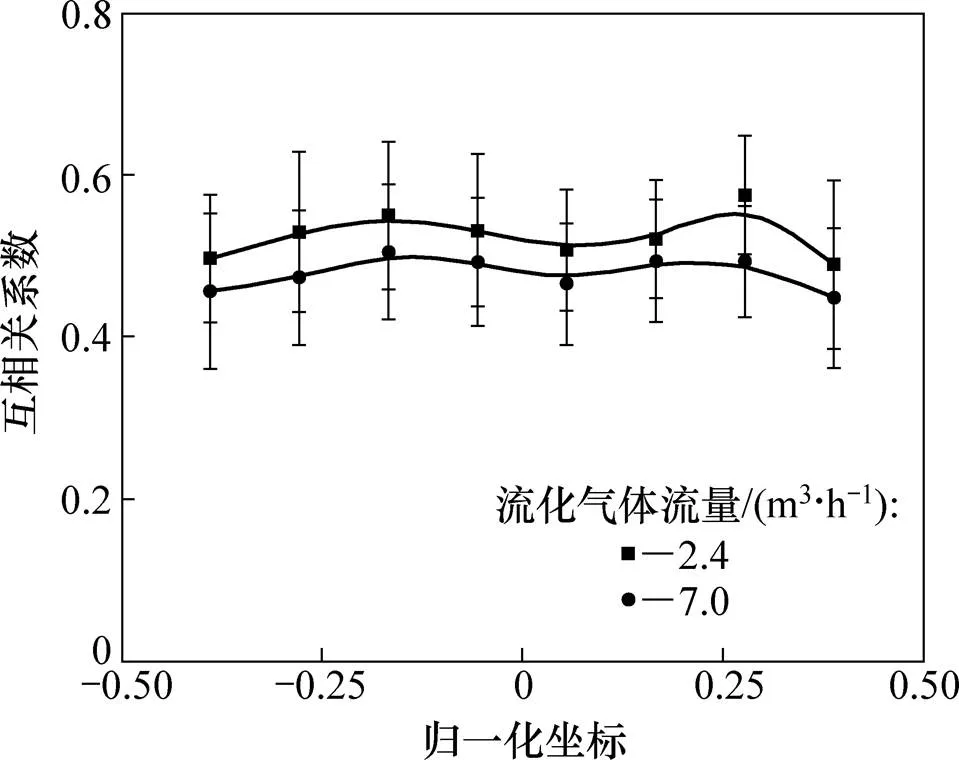
图5 不同流化气体流量下传感器所在截面处互相关系数的分布

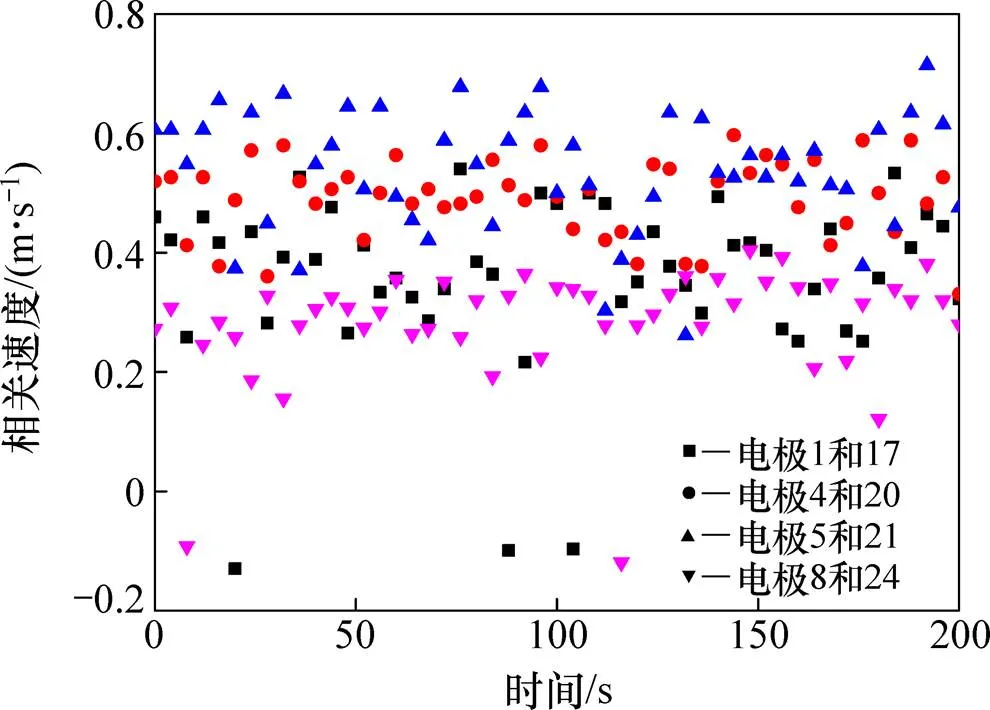
图6 流化气体流量为7 m3/h时流化床中心处与床壁附近的相关速度

图7所示为传感器所在截面固体颗粒的轴向速度分布。从图7可以看出：随着气流量增加，固体颗粒的轴向速度随之增加。并且颗粒的速度分布表明中间区域颗粒流速较高，而床壁附近的流速较低。产生以上结果的原因是：随着流化气量的增加，导致气泡的上升速度增加，由于气泡的曳力作用，颗粒的流速也会加快；另外，由于壁面效应的影响，床壁附近的颗粒流速会比中心区域的流速低。

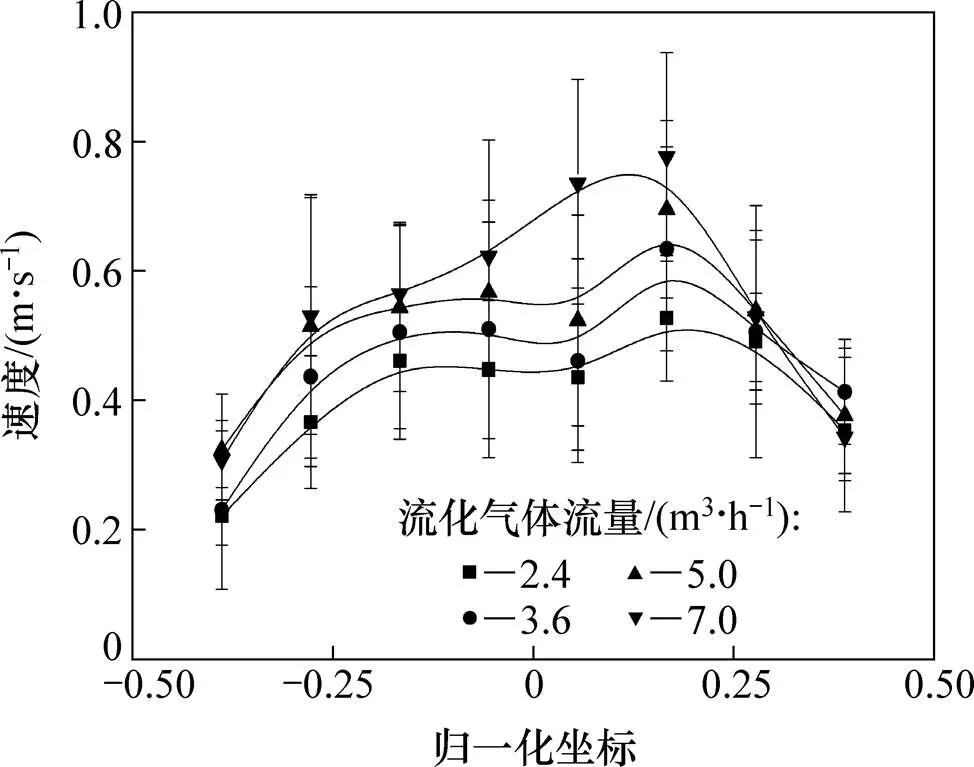
图7 不同流化气体流量下传感器所在截面固体颗粒的轴向速度分布

3.2 电荷分布测量

基于所有网状电极上的感应电荷并结合电荷分布重建算法，可以得到流化床截面处固体颗粒的电荷分布情况。由于直接测量电极上的感应电荷十分困难，并且静电信号均方根(RMS)是信号波动量的表征，可以反映电极上的感应电荷量[10]。本研究利用电极上静电信号的RMS来估算电极上的感应电荷量。静电信号的RMS与电极上感应电荷量的对应关系是通过电荷标定实验得到的。电容器上的电荷量与其上的电压成比例关系(=，其中为电容器的电容)。电荷标定实验中，电容器放在网状电极的中心处，电容器上的电压随时间变化，由此产生的时变静电场会在电极上感应出静电电荷，电极上静电电荷的变化会在后续信号调理电路中产生静电信号。由于电容器上的电压已知，电容器上的电荷就可以得到，根据有限元仿真获得的网状电极灵敏度分布可以计算出每个电极上的感应电荷，因此，可以求出静电信号RMS与电极上感应电荷之间的比例系数。利用该比例系数就可以通过静电信号的RMS估算电极上的感应电荷量。

当流化气体流量分别为2.4 m3/h和5.0 m3/h时，电极1和电极4上感应电荷的变化情况见图8。从图8可见：由于流化床中固体颗粒浓度和流速的不断变化，颗粒上的带电量会有很大波动，因此，造成了电极上感应电荷随时间的波动；在相同流化气体流量下，电极4的平均感应电荷量大于电极1的平均感应电荷量。产生这种偏差的原因是颗粒在流化床中心处和床壁附近的速度差，因此，在流化床截面不同位置的颗粒带电情况有很大差别，中心处电极的感应电荷量更大。

在不同气流量下，不同电极所得感应电荷结果的时间平均和相应的标准差如图9所示。与图8所示结果相同，流化床中心处电极的感应电荷量大于床壁附近电极的感应电荷量。并且所有电极上的平均感应电荷量随着气体流量的增大而增大。气泡上升速度随着气体流量的增大而增大，流化床内颗粒的运动变得更加复杂，由于颗粒间的相互作用加强，颗粒上的带电量会增加，因此，网状电极上的感应电荷也会增加。从图8还可以看出：中心处电极感应电荷量的标准差比床壁附近电极的相应结果大，并且随着气流量的增加，不同电极上的标准差值变大。这是由于流化床中心处颗粒运动更加剧烈，中心处电极的感应电荷量波动大。并且随着气流量增大，颗粒运动变得更加复杂，也会造成感应电荷量波动变大。

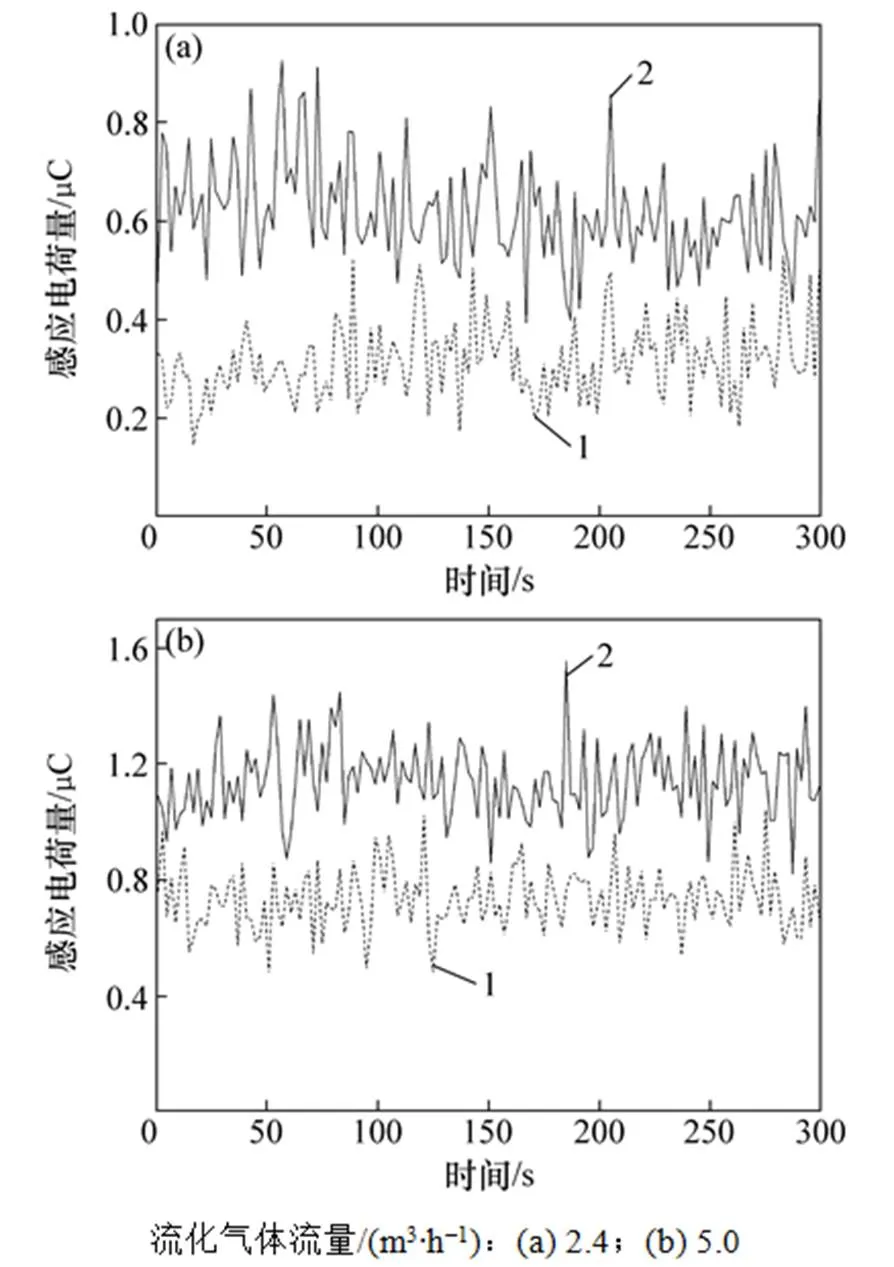
1—电极1；2—电极4。

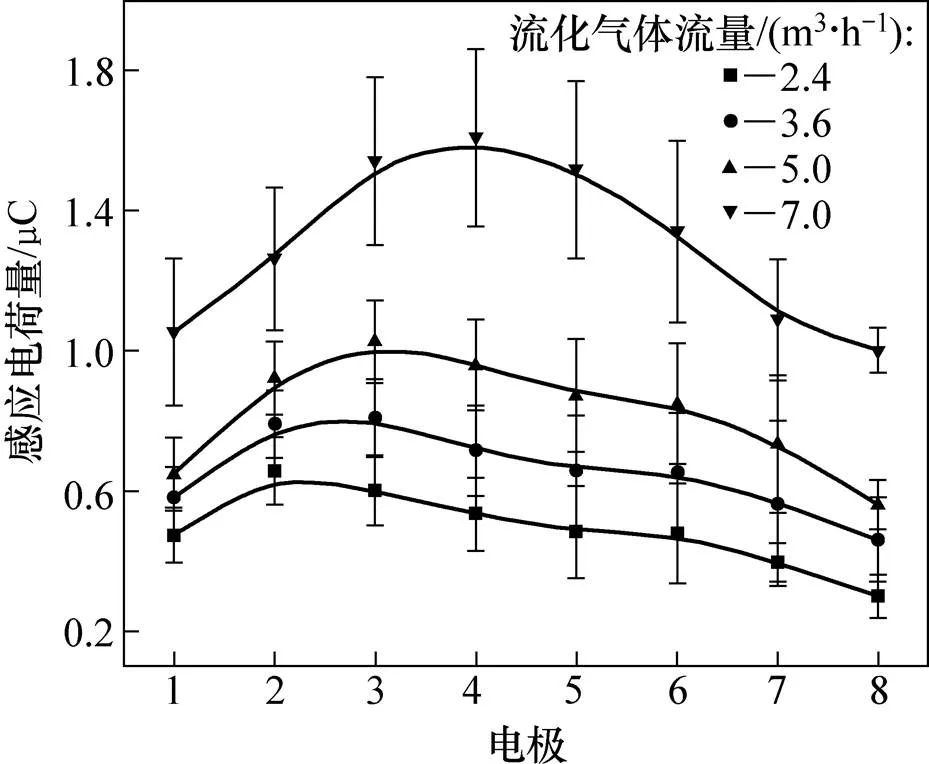
图9 不同气流量下不同电极所得感应电荷的时间平均和相应的标准差

根据已经获得的网状电极上的感应电荷量，利用文献[20]中所提出的电荷量重建算法，可以重建出网状电极所在截面处的电荷分布。图10所示为流化气体流量为7 m3/h时流化床截面处的电荷分布情况。图中右侧的色标表示电荷量。虽然在中心处电荷量高，总体上看流化床截面的电荷分布相对均匀。图中后侧床壁附近的电荷量低是由布风板造成的流化床布风不均匀引起的。

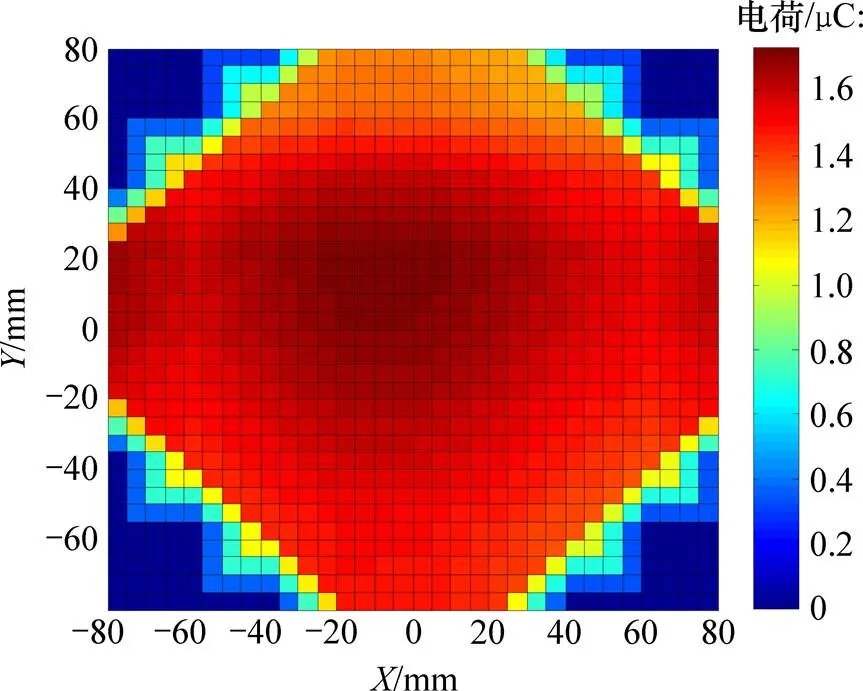
图10 流化气体流量为7 m3/h时流化床截面处的电荷分布

4 结论

1) 提出一种利用网状静电传感器测量鼓泡流化床中颗粒的速度廓形和电荷分布的方法。由于网状静电传感器可以获得更高和更加均匀的灵敏度分布，因此，非常适合测量流化床等复杂气固流动系统。为了证实该传感器的性能，在实验室规模的鼓泡流化床实验平台上进行实验研究。

2) 该测量系统可以得到传感器所在截面处固体颗粒的轴向速度分布，并且可以发现床壁附近的下落颗粒。根据电荷标定结果，本文提出利用静电信号的RMS估计网状电极上的感应电荷。通过分析不同气流量下不同电极的感应电荷变化规律，得出流化床中心处电极的平均感应电荷量大于床壁附近电极的平均感应电荷量，并且电极上的感应电荷量随着气流量的增大而变大。通过分析重建后的电荷分布情况，可以看出流化床截面处电荷分布相对均匀，相对于平均值的最大偏差小于24%。利用网状静电传感器获得的颗粒速度廓形和电荷分布，可以对流化床的运行参数进行监测，提高运行效率和产品质量。

[1] SHAFFER F, GOPALAN B, BREAULT R W, et al. High speed imaging of particle flow fields in CFB risers[J]. Powder Technology, 2013, 242: 86−99.

[2] LAVERMAN J A, ROGHAIR I, ANNALAND M V, et al. Investigation into the hydrodynamics of gas-solid fluidized beds using particle image velocimetry coupled with digital image analysis[J]. Canadian Journal of Chemical Engineering, 2008, 86(3): 523−535.

[3] MUELLER C R, HOLLAND D J, SEDERMAN A J, et al. Magnetic resonance imaging of fluidized beds[J]. Powder Technology, 2008, 183(1): 53−62.

[4] RASOULI M, BERTRAND F, CHAOUKI J. A multiple radioactive particle tracking technique to investigate particulate flows [J]. AICHE Journal, 2015, 61(2): 384−394.

[5] CHAN C W, SEVILLE J P K, PAEKER DJ, et al. Particle velocities and their residence time distribution in the riser of a CFB[J]. Powder Technology, 2010, 203(2): 187−197.

[6] QIAN X C, YAN Y, SHAO J Q, et al. Quantitative characterization of pulverized coal and biomass-coal blends in pneumatic conveying pipelines using electrostatic sensor arrays and data fusion techniques[J]. Measurement Science Technology, 2012, 23(8): 085307.

[7] QIAN X C, YAN Y. Flow measurement of biomass and blended biomass fuels in pneumatic conveying pipelines using electrostatic sensor arrays[J]. IEEE Transactions on Instrumentation. and Measurement, 2012, 61(5): 1343−1352.

[8] QIAN X C, HUANG X B, HU Y H, et al. Pulverized coal flow metering on a full-scale power plant using electrostatic sensor arrays[J]. Flow Measurement and Instrumentation, 2014, 40: 185−191.

[9] ZHANG W B, CHENG Y P, WANG C, et al. Investigation on hydrodynamics of triple-bed combined circulating fluidized bed using electrostatic sensor and electrical capacitance tomography[J]. Industrial Engineering Chemistry Research, 2013, 52(32): 11198−11207.

[10] ZHANG W B, YAN Y, YANG Y R, et al. Measurement of flow characteristics in a bubbling fluidized bed using electrostatic sensor arrays[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(3): 703−712.

[11] SOWINSKI A, SALAMA F, MEHRANI P. New technique for electrostatic charge measurement in gas-solid fluidized beds[J]. Journal of Electrostatics, 2009, 67(4): 568−573.

[12] SOWINSKI A, MILLER L, MEHRANI P. Investigation of electrostatic charge distribution in gas-solid fluidized beds[J]. Chemical Engineering Science, 2010, 65(3): 2771−2781.

[13] MACHIDA M, SCARLETT B. Process tomography system by electrostatic charge carried by particles[J]. IEEE Sensors Journal, 2005, 5(2): 251−259.

[14] ZHOU B, ZHANG J Y. A novel ECT–EST combined method for gas-solids flow pattern and charge distribution visualization[J]. Measurement Science and Technology, 2013, 24(7): 074003.

[15] CHEN A, BI H T, GRACE J R. Charge distribution around a rising bubble in a two-dimensional fluidized bed by signal reconstruction[J]. Powder Technology, 2007, 177(3): 113−124.

[16] HE B, BI H T, GRACE J R. Simultaneous measurements of particle charge density and bubble properties in gas-solid fluidized beds by dual-tip electrostatic probes[J]. Chemical Engineering Science, 2015, 123: 11−21.

[17] HE C, BI H T, GRACE J R. A novel dual-material probe for in situ measurement of particle charge densities in gas-solid fluidized beds[J]. Particuology, 2015, 21: 20−31.

[18] SUN J Y, YAN Y. Characterization of flow intermittency and coherent structures in a gas-solid circulating fluidized bed through electrostatic sensing[J]. Industrial Engineering Chemistry Research, 2016, 55(46): 12133−12148.

[19] SUN J Y, YAN Y. Non-intrusive characterisation of particle cluster behaviours in a riser through electrostatic and vibration sensing[J]. Chemical Engineering Journal, 2017, 323: 381−395.

[20] ZHANG W B, YANG B B, YAN Y, et al. Charge distribution reconstruction in a bubbling fluidized bed using a wire-mesh electrostatic sensor[C]//Proceedings of the IEEE International. Instrumentation and Measurement Technology Conference. Taipei, 2016: 28−32.

(编辑 杨幼平)

Monitoring of operation parameters in a bubbling fluidized bed using wire-mesh electrostatic sensors

ZHANG Wenbiao, YANG Binbin, CHENG Xufeng

(School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China)

In order to further study the flow dynamics of particles in the fluidized bed and optimize the operating parameters of the fluidized bed reactor, real-time monitoring of the solids velocity profile and the charge distribution in the fluidized bed is needed. Due to the high and uniform sensitivity distribution, the wire-mesh electrostatic sensors were installed in a lab-scale bubbling fluidized bed to measure the velocity profile and the charge distribution of solid particles. Cross-correlation calculation of the upstream and downstream signals was applied to calculate the velocity profile of solid particles. Induced charges on the electrodes of the wire-mesh sensors were estimated by root mean square (RMS) of the electrostatic signals. Based on charge distribution reconstruction algorithm, cross sectional charge distribution was reconstructed using the induced charges from all the electrodes. The results indicate that the wire-mesh sensors can capture the falling particles near the wall. Because of the influence from the solids velocity profile, induced charge on electrode in the center of the bed is higher than that near the wall and the reconstructed charge distribution in the cross section of the bubbling bed is relatively uniform.

wire-mesh electrostatic sensors; bubbling fluidized bed; charge distribution; velocity profile

TH89

A

1672−7207(2018)04−1011−07

10.11817/j.issn.1672−7207.2018.04.032

2017−04−16；

2017−07−09

国家自然科学基金资助项目(61403138)；北京市自然科学基金资助项目(3162031)(Project(61403138) supported by the National Natural Science Foundation of China; Project(3162031) supported by Beijing Natural Science Foundation)

张文彪，博士，讲师，从事多相流检测技术研究；E-mail：wbzhang@ncepu.edu.cn