基于自治布尔网络的高速物理随机数发生器研究

马荔，张建国，李璞，徐航，王云才



基于自治布尔网络的高速物理随机数发生器研究

马荔1, 2，张建国1, 2，李璞1, 2，徐航1, 2，王云才1, 2

(1. 太原理工大学 物理与光电工程学院，山西 太原，030024；2. 新型传感器与智能控制教育部和山西省重点实验室，山西 太原，030024)

利用确定性的数学算法可产生快速伪随机数，然而其具有可预测性，难以确保信息安全。从混沌物理熵源中提取的物理随机数具有统计无偏和不可预测性，但是受限于传统混沌电路的带宽瓶颈，随机数的实时产生速率无法有效提高，为此，设计实现一种基于自治布尔网络的宽带混沌振荡器。研究结果表明：利用该装置可产生速率达10 Gbit/s的物理随机数序列；所产生的物理随机数序列具有良好的随机统计特性；该装置可便捷地应用于数据加密、高速保密通信等领域。

自治布尔网络；混沌；高速物理随机数发生器

随机数在科学计算、数字通信、光纤传感、雷达测距[1−4]等领域被广泛应用。特别是在保密通信领域，随机数发生器是通信系统中的重要组成部分。随机数发生器分为2种：伪随机数发生器和物理随机数发生器。伪随机数是通过某种确定性的算法(如线性同余法[5])结合“种子”(初值)而产生，具有很高的产生速率，但是，伪随机数固有的周期性使其存在被预测和破解的可能，无法确保信息的安全。相对于伪随机数，物理随机序列无法预测，不可再现，因此，能更好地保证传输信息的安全。物理随机数的产生是建立在一种称为物理熵源的随机信号源的基础上，如电阻热噪声[6]、振荡环中的相位抖动[7]、混沌激光[8−10]、自发辐射中的量子噪声[11]等。其中，基于混沌电路的物理熵源具有结构简单、功耗低、易集成等特点, 目前已经产生多种物理随机数发生器方案[12−13]。但是，受限于混沌电路的熵源带宽，此类物理随机数发生器的速率仅为数kbit/s至数十Mbit/s，不能满足现代通信速率的需求。为此，本文作者设计一种基于自治布尔网络的振荡器，当其工作于混沌状态时，振荡器固有的周期抖动(由逻辑门热噪声引起，抖动范围为数十ps)经混沌非线性放大增强了约2个数量级(抖动范围达数ns)，并产生了高熵值。通过1个高频时钟对增强的周期抖动进行采样，利用样本值的不确定性将采样序列转换成物理随机序列。该方案具有结构简单，易于集成等优点。本文提出的基于自治布尔网络的随机数发生器可以在现场可编程逻辑门阵列 (FPGA)上实现, 并可实时产生10 Gbit/s以上速率的随机数序列，性能优于现有混沌随机数发生器。

1 混沌熵源数值仿真与实验电路特性分析

1.1 混沌熵源数值仿真

本文设计的基于自治布尔网络的振荡器如图1所示。网络中含有若干可执行逻辑运算的结点，组成具有双向耦合关系的环状拓扑结构。图中每个结点代表1个具有三输入三输出功能的逻辑门，执行异或(XOR)或异或非(XNOR)操作。逻辑门的真值如图1(b)所示。利用GHIL等[14]提出的布尔延迟方程(BDEs, Boolean delay equations)如下式所示：

然而，上述结论是在将逻辑门视为理想器件(响应速度无限快)情况下得出的，而在真实电路中，任何逻辑器件都无法响应变化速度过快的信号，即存在所谓的非线性低通滤波效应[15]。利用SPICE软件对图1(a)中的网络建立更接近实际电路的仿真模型：结点个数设置为7，网络中任选1个结点执行XNOR操作，而其余6个结点执行XOR操作；则利用RC滤波器(电阻−电容滤波器)来模拟，通过改变电阻、电容即可实现延迟时间量的连续调节，同时还能模拟逻辑器件的低通效应。仿真结果表明：1) 当网络中所有延迟时间设置为相等，即=30 ps时，振荡器呈现周期性振荡状态；2) 当网络中的延迟时间设置为不完全一致即=(30±3) ps时，振荡器进入随机振荡状态，出现了所谓的布尔混沌现象[16]。

1—XNOR逻辑门；2~7—XOR逻辑门。

1.2 混沌熵源实验电路特性分析

1.2.1 自治布尔网络振荡器电路特性

利用现场可编程门阵列(Altera Cyclone IV FPGA cyclone IV，EP4CE10F17C8N)实现图1所示的自治布尔网络振荡器。由于在实际电路中，各结点(逻辑门器件)之间的物理路径很难做到完全一致，导致延迟时间之间存在微小差异，因此，正如仿真预测结果一样，自治布尔网络出现了随机振荡。振荡信号的时序、频谱和自相关分别如图2(a)~(c)所示。同时，进一步分析该振荡信号频率“抖动”的概率密度分布(PDF)，结果如图2(d)所示，总体呈泊松分布。值得一提的是，该频率“抖动”比传统意义上由热噪声引起的频率抖动(数十ps)增加了约2个数量级，且更大的“抖动”意味着从中可提取实时速率更高的随机数序列。

图2 自治布尔网络振荡器的

1.2.2 最大李雅普诺夫指数

根据小数据法[17]计算上述自治布尔网络振荡器的最大李雅普诺夫指数，具体计算步骤如下。

1) 采集一段40 μs的混沌电压时间序列()，并通过与阈值(cc/2)比较，将其转换成布尔变量()∈{0，1}，如图3(a)所示。当()＜cc/2时，()=0；当()＞cc/2时，()=1。其中，cc是FPGA中逻辑异或门和异或非门的工作电压。

2) 参考文献[15]，计算布尔距离函数()：

选取0=10 ns，=0.01，振荡器输出信号的最大李雅普诺夫指数ab=0.22 ns−1，如图3(b)所示；最大李雅普诺夫指数值为正，表明了输出振荡信号的混沌属性。

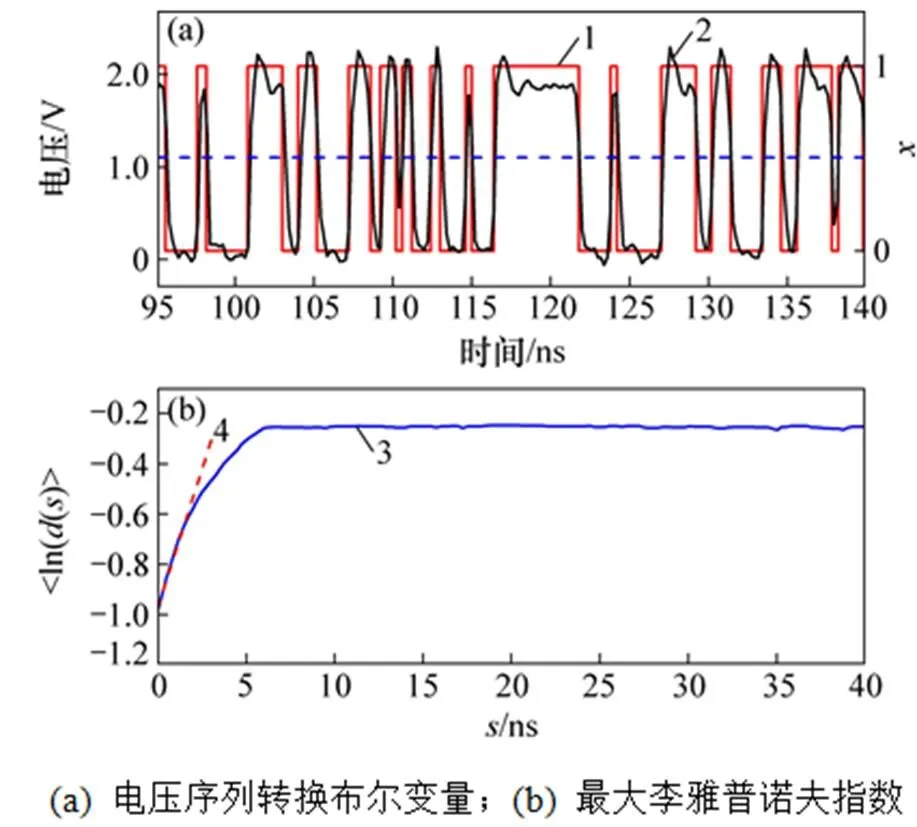
1—布尔电压；2—混沌电压；3—相邻轨迹变化；4—指数率。

2 随机数发生器单元模块的实现

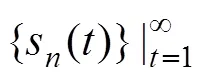
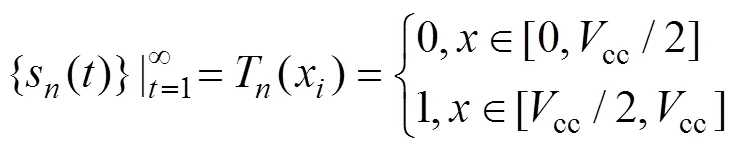
本随机数发生器单元模块具有如下优点：1) 以最少的器件个数实现了自治布尔网络物理熵源，产生了随机性较好的混沌信号；2) 随机数发生器模块占用FPGA芯片资源极少，仅需7个逻辑门和11个D型触发器(共18个逻辑单元LE)；3) 只需相应增加模块的级数就可以实时产生更高速率的随机数, 例如FPGA工作频率为100 MHz，产生的随机数速率可达100×L Mbit/s。本文中设置模块数量为100，随机数发生器速率即可达到10 Gbit/s，此时总计需要1 800个LE，以目前使用FPGA芯片的容量及规模，只占其资源的17%(通常为104个LE)。因此，本随机数发生器的速率还有较大的提升空间。

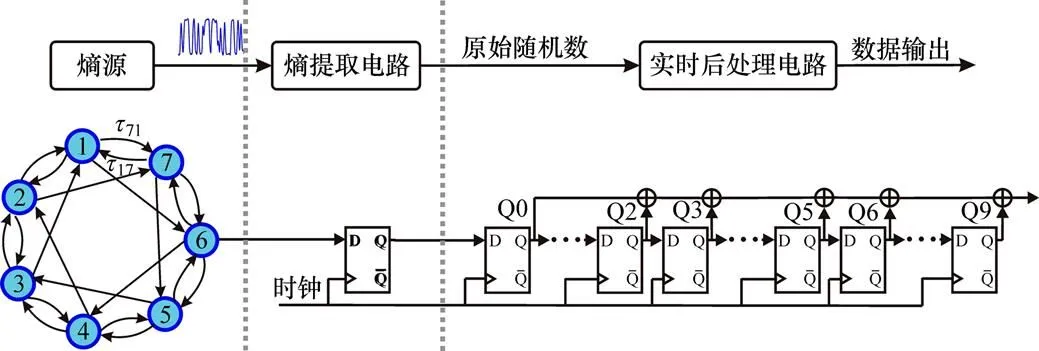
图4 基于自治布尔网络物理熵源的随机数发生器单元模块

图5所示为高速10 Gbit/s随机数发生器，图中clk为FPGA输入时钟。

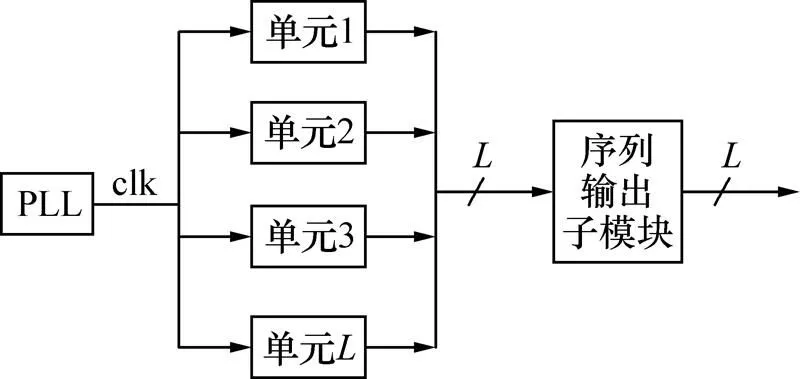
图5 高速10 Gbit/s随机数发生器

3 随机性测试

为了测试所产生随机数的质量，对其进行NIST[18]及DIEHARD[19]随机性检验测试。以美国国家标准与技术研究院提供的NIST SP800-22测试为例，采集1 Gbit随机数(1 000组，每组1 Mbit)进行15项测试，显著水平=0.01。测试结果以值和概率给出。当值大于0.01，概率超过0.980 6表明随机数通过了相应测试，如表1所示。

表1 美国国家标准与技术研究院测试结果

基于自治布尔网络振荡器的随机数发生器产生的 1 Gbit随机数能够通过NIST全部随机数测试标准，表明其具备良好的随机性。

4 结论

1) 设计了一种基于自治布尔网络振荡器的高速物理随机数发生器，该装置可产生速率达10 Gbit/s的物理随机数序列；NIST测试结果表明该装置所产生的随机序列具有良好的统计学特性。

2) 该设计还具有结构紧凑、易于集成制造等优点，可便捷地应用于数据加密、保密通信、密钥产生等领域。

[1] 萧宝瑾, 仝海丽, 张建忠, 等. 硬件加密的扩频通信方案[J]. 物理学报, 2011, 60(8): 81−86. XIAO Baojin, TONG Haili, ZHANG Jianzhong, et al. Spread spectrum communication based on hardware encryption[J]. Acta Physica Sinica, 2011, 60(8): 81−86.

[2] ZADOK A, ANTMAN Y, PRIMEROV N, et al. Random-access distributed fiber sensing[J]. Laser & Photonics Reviews, 2012, 6(5): L1−L5.

[3] AI X, NOCK R, RARITY J G, et al. High-resolution random-modulation cw lidar[J]. Applied optics, 2011, 50(22): 4478−4488.

[4] 苏桂平, 吕述望, 程志蓉. 口令的安全分析及真随机数在金融安全中的应用[J]. 计算机工程与应用, 2002, 38(8): 140−141. SU Guiping, LÜ Shuwang, CHENG Zhirong. Analysis of password security and application of real random number in the finance security[J]. Computer Engineering and Applications, 2002, 38(8): 140−141.

[5] LEHMER D H。 Mathematical methods in large-scale computing units[M]. Boston: Harvard University Press, 1951: 141−146.

[6] PETRIE C S, CONNELLY J A. A noise-based IC random number generator for applications in cryptography[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2000, 47(5): 615−621.

[7] BUCCI M, GERMANI L, LUZZI R, et al. A high speed truly IC random number source for smart card microcontrollers[C]//9th International Conference on Dubrovnik, Croatia, Germany: IEEE, 2002: 239−242.

[8] UCHIDA A, AMANO K, INOUE M, et al. Fast physical random bit generation with chaotic semiconductor lasers[J]. Nature Photonics, 2008, 2(12): 728−732.

[9] WANG Anbang, LI Pu, ZHANG Jianguo, et al. 4.5 Gbps high-speed real-time physical random bit generator[J]. Optics Express, 2013, 21(17): 20452−20462.

[10] LI Pu, WANG Yuncai, ZHANG Jianzhong. All-optical fast random number generator[J]. Optics express, 2010, 18(19): 20360−20369.

[11] KWON O, CHO Y W, KIM Y H. Quantum random number generator using photon-number path entanglement[J]. Applied optics, 2009, 48(9): 1774−1778.

[12] CALLEGARI S, ROVATTI R, SETTI G. Embeddable ADC-based true random number generator for cryptographic applications exploiting nonlinear signal processing and chaos[J]. IEEE Transactions on Signal Processing, 2005, 53(2): 793−805.

[13] CICEK I, PUSANE A E, DUNDAR G. A new dual entropy core true random number generator[J]. Analog Integrated Circuits and Signal Processing, 2014, 81(1): 61−70.

[14] GHIL M, ZALIAPIN I, COLUZZI B. Boolean delay equations: A simple way of looking at complex systems[J]. Physica D: Nonlinear Phenomena, 2008, 237(23): 2967−2986.

[15] ZHANG R, CAVALCANTE H L D S, GAO Z, et al. Boolean chaos[J]. Physical Review E, 2009, 80(4): 045202.

[16] ROSIN D P. Dynamics of Complex Autonomous Boolean Networks[M]. Berlin, Germany: Springer International Publishing, 2015: 57−79.

[17] KANTZ H, SCHREIBER T. Nonlinear time series analysis[J]. Technometrics, 1997, 47(3): 381−381.

[18] National Institute of Standards and Technology. Nist statistical tests suite[EB/OL]. [2014−07−16]. http://cs-rc.nist.Gov/groups/ ST/toolkit/rng/stats_test.html

[19] MARSAGLIA G. DIEHARD: a battery of tests of randomness[EB/OL]. [2009−06−06] http://stat.fsu.edu/~geo/ diehard. Html.

(编辑 杨幼平)

High-speed physical random number generator based on autonomous Boolean networks

MA Li1, 2, ZHANG Jianguo1, 2, LI Pu1, 2, XU Hang1, 2, WANG Yuncai1, 2

(1. College of Physics and Optoelectronics, Taiyuan University of Technology, Taiyuan 030024, China; 2. Key Laboratory of Advanced Transducers and Intelligent Control System, Ministry of Education, Taiyuan 030024, China)

Using deterministic mathematical algorithms can produce fast pseudo-random numbers. However, their predictability makes them difficult to guarantee the security of communication. Unpredictable random numbers can be extracted from chaotic circuits, called physical random number generators (physical-RNGs). But the bandwidths of the conventional chaotic circuits limit their generation bit rates. A novel physical-RNG by utilizing the autonomous Boolean network which can produce wideband chaotic signals was designed. The results show that the physical-RNG can produce physical random bits stream at a speed up to 10 Gbit/s. The physical random numbers generated by the physical-RNG own good random characteristics. The physical-RNG can be conveniently applied in data encryption and secure communications.

autonomous Boolean network; chaos; high-speed physical random number generator

TN791

A

1672−7207(2018)04−0888−05

10.11817/j.issn.1672−7207.2018.04.016

2017−04−29；

2017−06−22

国家自然科学基金资助项目(51404165, 616013190, 61505137, 61475112, 61501414, 61771439)(Projects(51404165, 616013190, 61505137, 61475112, 61501414, 61771439) supported by the National Natural Science Foundation of China)

王云才，博士，教授，从事混沌激光产生与应用及光通信等研究；E-mail：wangyc@tyut.edu.cn