基于包络解调滤波的滚动轴承复合故障诊断

刘东东，程卫东，温伟刚，万广通

基于包络解调滤波的滚动轴承复合故障诊断

刘东东，程卫东，温伟刚，万广通

(北京交通大学 机械与电子控制工程学院，北京，100044)

针对在变转速工况下进行滚动轴承复合故障诊断时，由于故障间的相互作用使得多种故障特征混叠在一起，彼此干扰，造成误判﹑漏判等问题，以及时域滤波过程中共振频带参数难以获得这一问题，提出基于包络解调滤波的滚动轴承复合故障诊断方法。首先，使用多项式函数拟合轴承转速，并根据轴承各部分的故障特征频率系数和转速信息计算瞬时故障特征频率(IFCF)趋势线；其次，根据各部分IFCF趋势线的拟合函数，构造解调算法的相位函数，对原始信号经过Hilbert变换得到的包络信号解调；最后，以各部分IFCF拟合函数的初始值为中心频率构造窄带巴特沃斯带通滤波器，对解调信号进行滤波处理，并对滤波后的信号进行快速傅里叶变换(FFT)得到包络解调滤波信号的频谱。研究结果表明：该算法使轴承IFCF的能量集中在初始值的位置，使用巴特沃斯带通滤波器便可以在包络信号中提取解调后的故障信息。该方法既克服了转速变化引起的“频率模糊”现象，又避免了时域滤波中共振频带难以确定的问题。仿真算例和应用实例证明了该算法的有效性。

变转速；滚动轴承；复合故障诊断；解调算法；瞬时故障特征频率；巴特沃斯带通滤波器

滚动轴承因工作环境恶劣，且常处于变载荷﹑变转速的工况中，极易发生局部故障[1−2]。在实际工况中，故障往往不会单独出现，一种故障往往会引起其他故障的发生[3]。复合故障即为同时存在2个或者多个互相联系﹑交叉影响的故障。由于故障间的相互作用，多种故障特征混叠在一起，彼此干扰和不同故障的强弱不平衡给轴承的复合故障诊断带来困难。轴承的局部故障和变转速的工作模式会引起共振频率发生调制现象[4]。而轴承的不同部位(如外圈﹑内圈或者滚动体)的调制情况不一致，因此，当轴承存在复合故障时，尤其是在变转速的工作条件下，其故障诊断遇到了挑战。针对轴承复合故障的诊断，人们进行了许多研究。王晓冬等[5]以峭度为优化目标，对多小波进行自适应构造，再对信号进行冗余分解，得到特征频率的相对能量，根据相对能量比选择敏感频带，实现对复合故障的诊断。明安波等[6]提出了小波−频谱自相关算法，采用正交小波基函数将信号分解为多个子信号后，再对子信号进行频谱自相关分析，有效地提取故障特征。CHEN等[7]提出了改进的CICA算法，并有效地应用于单通道轴承复合故障诊断。周俊等[8]将盲解卷积、形态滤波和频域压缩感知重构的稀疏分量分析相结合，用于轴承复合故障声学诊断。然而，这些算法都仅限于平稳或者转速波动较小状态下轴承复合故障诊断，在实际工况中，轴承经常受到变转速、变载荷等的影响。阶比跟踪技术是变转速工况下最常用的滚动轴承的故障特征提取方法[9−10]。然而，使用阶比跟踪技术处理复合故障信号时，由于不同故障之间相互干扰、交叉，使得包络阶比谱存在诸多干扰项。由于故障强弱不一，较小故障引起的峰值还可能淹没在噪声中。另外，阶比分析方法还存在理论缺陷。SAAVEDRA等[11]的研究表明计算阶比跟踪算法中时域向角域转化用的插值算法存在一定误差。CHENG等[12]证明阶比跟踪技术存在包络畸变，影响判断精度。轴承故障诊断中一个重要的环节是降噪。谱峭度滤波是轴承故障诊断中最常用的滤波算法。当轴承振动信号中混有强背景噪声(如齿轮噪声)时，谱峭度滤波算法不能有效判断轴承共振频率的中心频率和带宽[13]。以经验模态分解(empirical mode decomposition, EMD)为基础的降噪算法包括EMD[14]、平均经验模态分解[15]、总体平均经验模态分解[16]和局部均值分解[17]，这些滤波算法适用于平稳状态下信号的分解，对于非平稳状态下的轴承振动信号的处理常常结合角域采样，但是重采样过程计算量比较大。通过分析，现有的对于轴承振动信号的滤波基本都是选择在时域处理，通过降噪处理，提取轴承共振频带。然而，时域滤波受到弱背景噪声或者恒转速的限制。广义解调时频分析算法可以将时频分布是倾斜、非线性的信号转换成时频分布是平行于时间轴的信号[18]。广义解调时频算法最初应用于语音信号处理，由于其非常适用于处理多分量的调幅−调频信号，该算法已经开始应用于机械设备的故障诊断。本文作者将广义解调时频分析算法中涉及到的广义解调函数用于滚动轴承包络时域信号中。根据瞬时故障特征频率(instantaneous fault characteristic frequency, IFCF)[19]在包络时频谱(envelope time frequency representation, ETFR )中的分布特点，使用解调函数处理包络时域信号，使随时间变化的IFCF能量集中于起始频率位置。针对变转速工况下滤波频带选择困难这一难题，避开在时域信号中滤波，选择在包络信号中使用带通滤波算法对解调后的故障特征频率进行提取。

1 算法部分

1.1 广义解调算法

广义解调算法是1种新的处理非平稳信号的方法。该算法能将倾斜分布的瞬时频率成分转换为平行于时间轴的线性成分(利用对应的相位函数对其解调)，其本质为广义傅里叶变换。对于信号()，其广义傅里叶变换G()的定义为

1.2 巴特沃斯滤波器

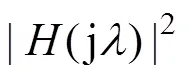
其中：为常数参数；为滤波器阶数；为归一化低通截止频率，=/p；为角频率；p为截止频率。

巴特沃斯低通滤波器的特性由其阶数确定。当增加时，滤波器的特性曲线变得陡峭，在角频率=p处，特性曲线将在通带的更大范围内接近于1，在阻带内更迅速地接近于0，因而，振幅特性更接近于理想的矩形频率特性。

巴特沃斯滤波器传递函数()的表达式为

去掉归一化的影响可以得到传递函数()：

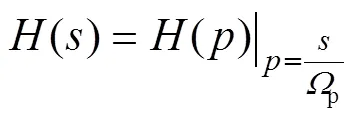
获得低通滤波器之后，带通滤波器的传递函数bp()可以由低通滤波器转换得到：

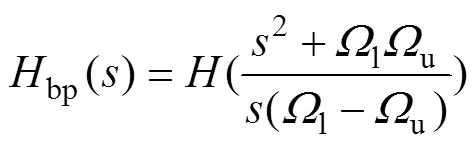
其中：l和u为下限和上限截止频率。

1.3 诊断算法流程图

当滚动轴承发生故障时，滚动轴承的IFCF及其倍频在ETFR中表现出明显的峰值，因此ETFR中存在清晰的有规律变化的IFCF趋势线。从轴承振动信号的频谱图中寻找IFCF与转频的关系以判断轴承故障。频谱图识别中会遇到2个问题，即转速变化使故障特征频率失去周期性，频谱图出现“频率模糊”现象；复合故障相互干扰、混叠，结合背景噪声，将使得频谱图存在诸多干扰项。

轴承各部分的IFCF与轴承转速存在固定的比值关系，当转速变化时，转频与时间轴形成一定的夹角，IFCF也就与时间轴形成相同的夹角。而且轴承各部分的IFCF与转频的比例关系可以通过轴承的几何参数确定。假设轴承出现了外圈﹑内圈或者滚动体出现故障，依据转频，便可以估计轴承各部分的IFCF。通过估计的IFCF便可以求得解调算法的相位()。同时，拟合函数的初始值可以作为巴特沃斯滤波器的中心频率，以此来进行对ETFR进行解调滤波。其具体步骤如下：

1) 对原始信号进行Hilbert变换得到包络信号。

2) 使用多项式函数拟合轴承转速，并以此确定轴承外圈﹑内圈和滚动体的IFCF的拟合函数。

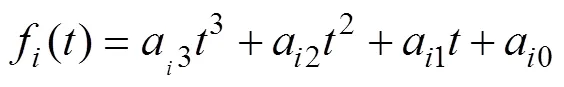
式中：=1，2或3；1()，2()和3()分别为外圈﹑内圈和滚动体IFCF的拟合方程；a0，a1，a2和a3均为常数。

3) 根据f()分别求得调函滤波的相位函数1，2和3：

式中：=1，2或3。

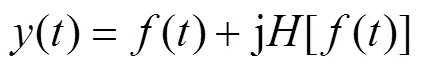
4) 利用IFCF的拟合函数f()的初始值a0为中心频率，width为带宽，构造窄带巴特沃斯带通滤波器，对解调信号滤波得到解调滤波信号。

5) 对解调滤波信号进行FFT得到解调滤波信号的频谱图，根据频谱图完成故障诊断。

2 仿真分析

为了验证提出算法的有效性，构造变转速工况下的轴承复合故障的仿真模型bearing()进行分析。仿真模型bearing()由外圈故障引起的冲击成分1()﹑内圈故障引起的冲击成分2()和高斯噪声成分()构成：

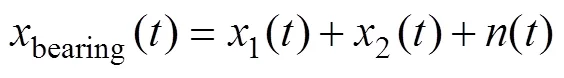
故障轴承的冲击成分()的表达式如下：

式中：为信号长度；A为第个冲击的幅值；为结构衰减系数；r为轴承共振频率；()为单位阶跃函数；t表示第个冲击出现的时间，

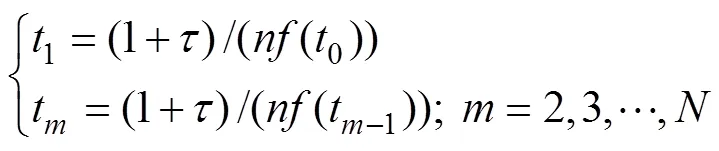
()为轴承转速；为由滚动体滑移引起的冲击间隔之间的误差，其取值一般为0.01~0.02；为每转的冲 击数。

轴承外圈和内圈故障特征系数分别设置为o=3.5和i=2.6，截取3~6 s的仿真数据进行分析。通过计算，此时间段内轴承转频为()=10+35。

表1 仿真信号参数

图1所示为根据式(8)构造的仿真信号的时域波形图。图2所示为仿真信号经过Hilbert变换得到的包络信号，对包络信号进行STFT变换得到ETFR，如图3所示。从ETFR可以看出IFCF由于转速的变化而表现出与时间轴呈一定夹角。

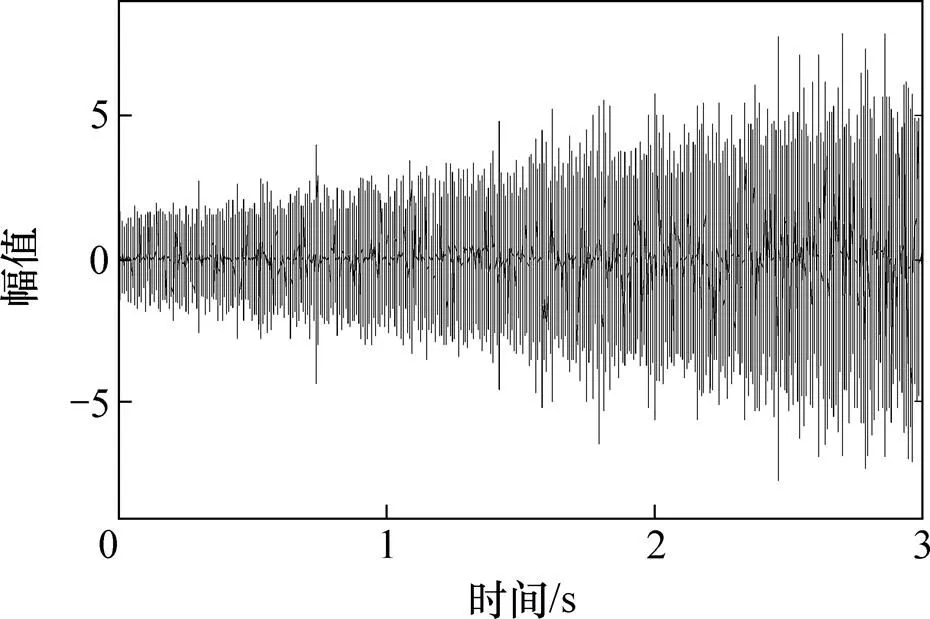
图1 仿真信号的时域波形图

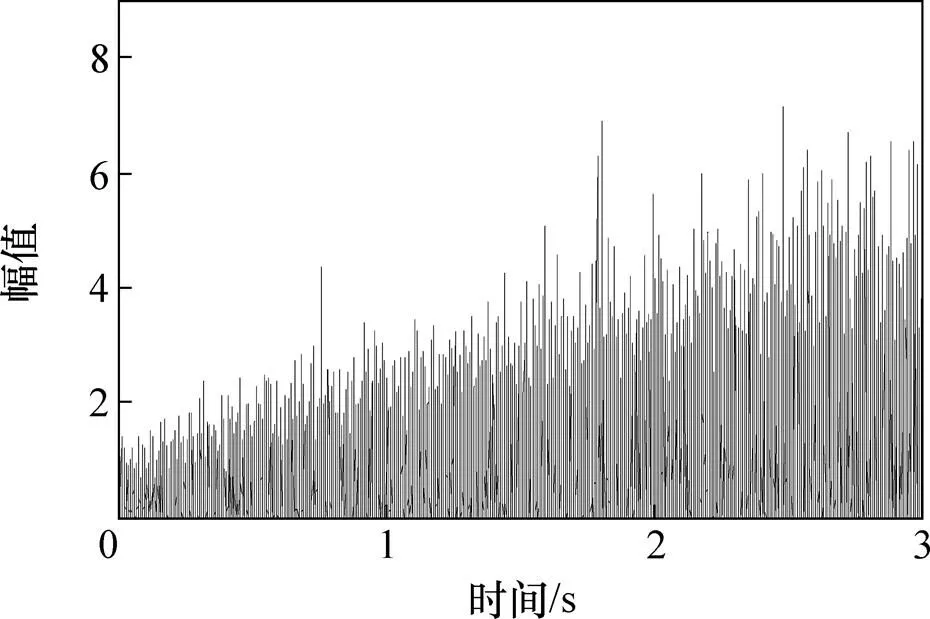
图2 仿真信号的包络信号

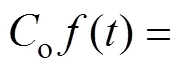
为了防止出现误判，将式(8)中2()设置为0，模拟轴承只出现外圈故障。通过以上分析算法处理此数据得到频谱，如图9所示。由图9可知：外圈故障解调滤波信号只在121.77 Hz处出现峰值，由此判断轴承只发生外圈故障。因此，提出的算法不会出现误判情况。

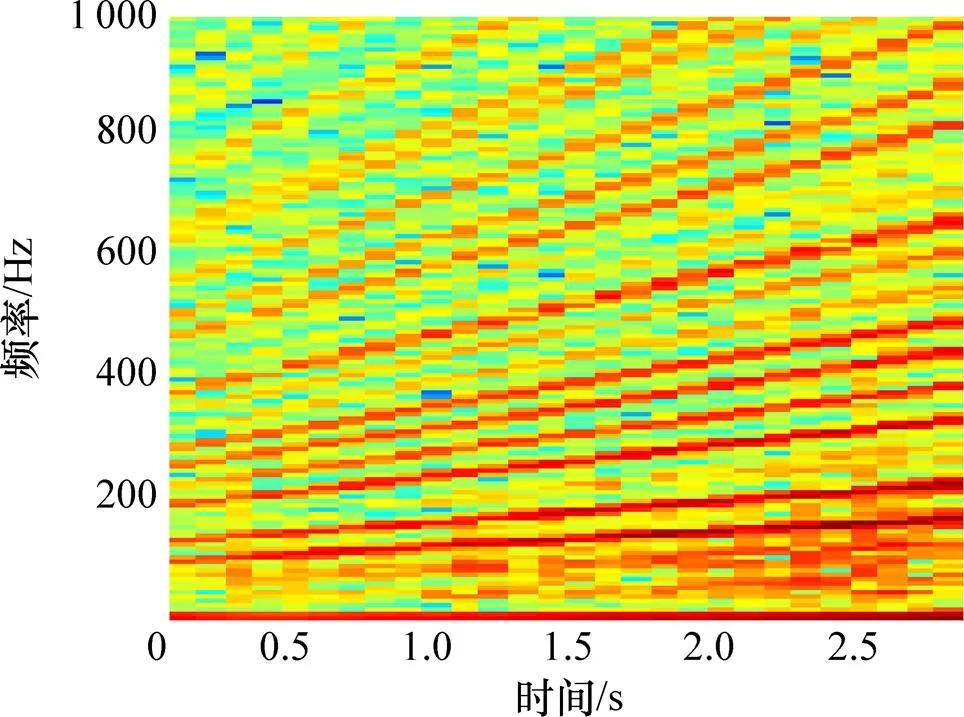
图3 仿真信号的ETFR

图4 仿真信号的解调ETFR

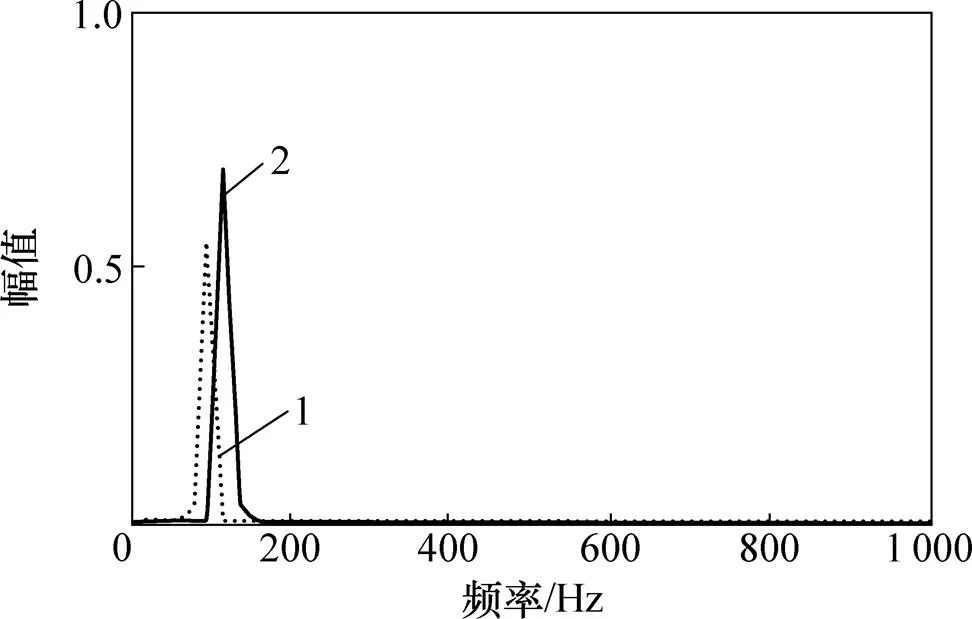
1—滤波波器F1；2—滤波器F2。

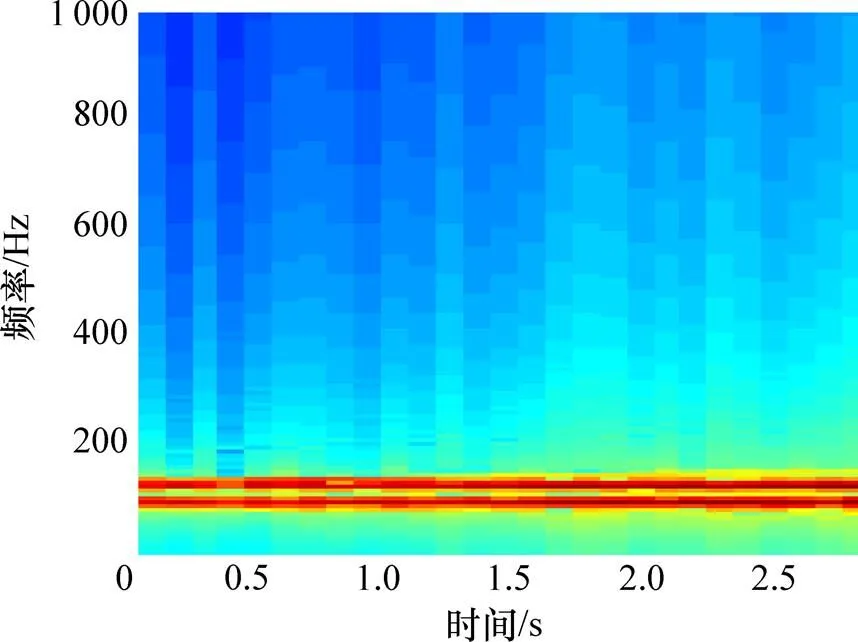
图6 仿真信号的解调滤波ETFR

图7 仿真信号的解调滤波频谱

图8 仿真信号的包络频谱

图9 外圈故障解调滤波信号的频谱

3 实验验证

利用北京交通大学的实验台测取的变转速工况下的轴承振动信号对提出算法的有效性进一步验证。使用激光加工实验轴承，模拟外圈和内圈出现裂纹。试验台结构和实验轴承如图10所示。实验轴承的具体参数如表2所示。

图10 试验台结构及实验轴承

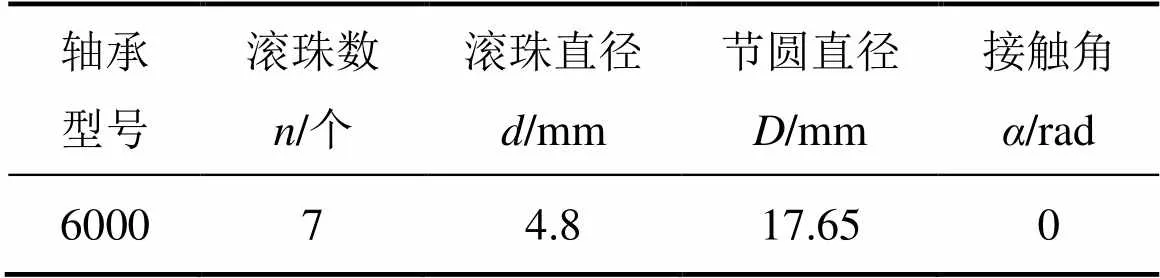
表2 目标轴承参数

根据表2中滚动轴承的参数计算得到实验轴承的外圈、内圈以及滚珠所对应的故障特征系数分别为o=2.548，i=4.452和b=1.7。采样频率为24 kHz，采样时间为10 s，其转速的变化范围为29.4~64.5 Hz。

图11所示为实测信号的时域波形图。原始信号经过Hilbert变换得到包络信号，再对包络信号进行STFT变换得到ETFR，如图12所示。从图12可以看出IFCF由于转速的变化而表现出与时间轴呈一定 夹角。

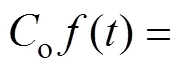
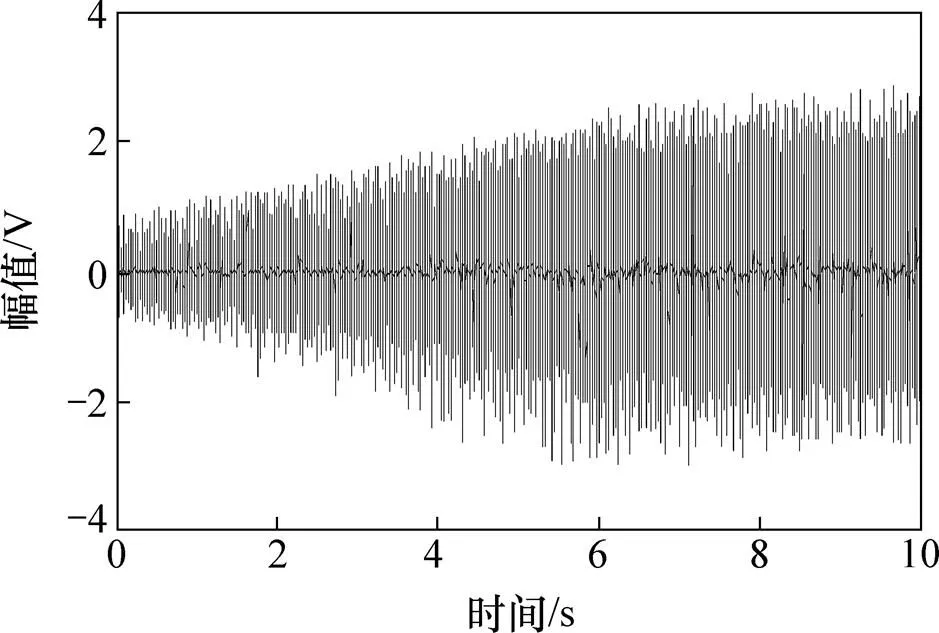
图11 实测信号的时域波形

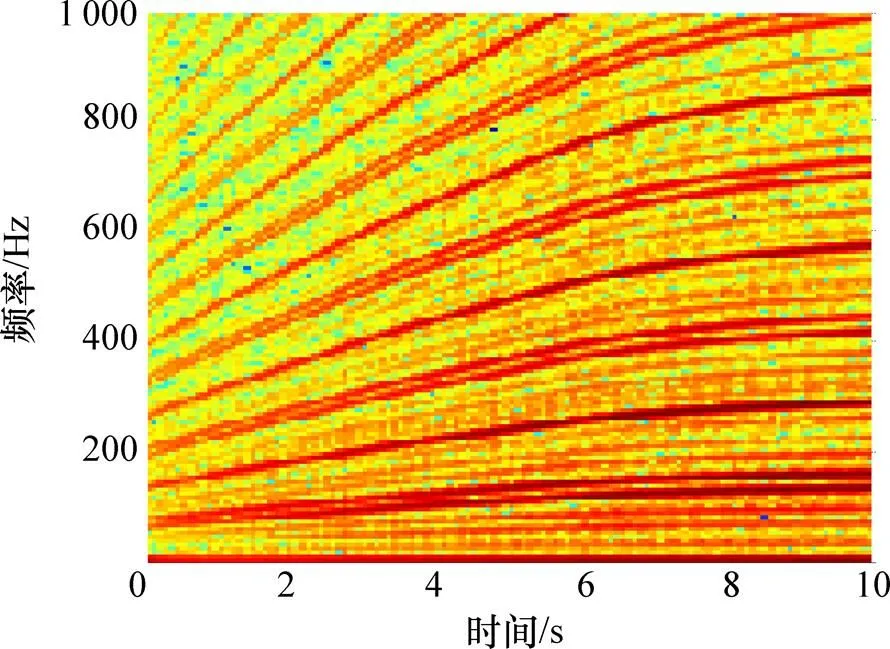
图12 实测信号的ETFR

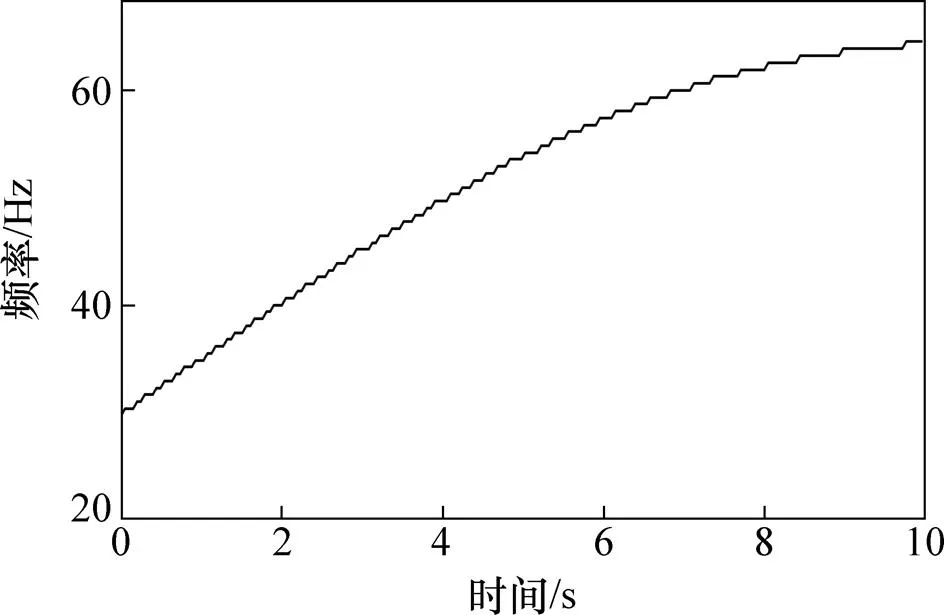
图13 转频趋势线

图14 实测信号的解调滤波ETFR

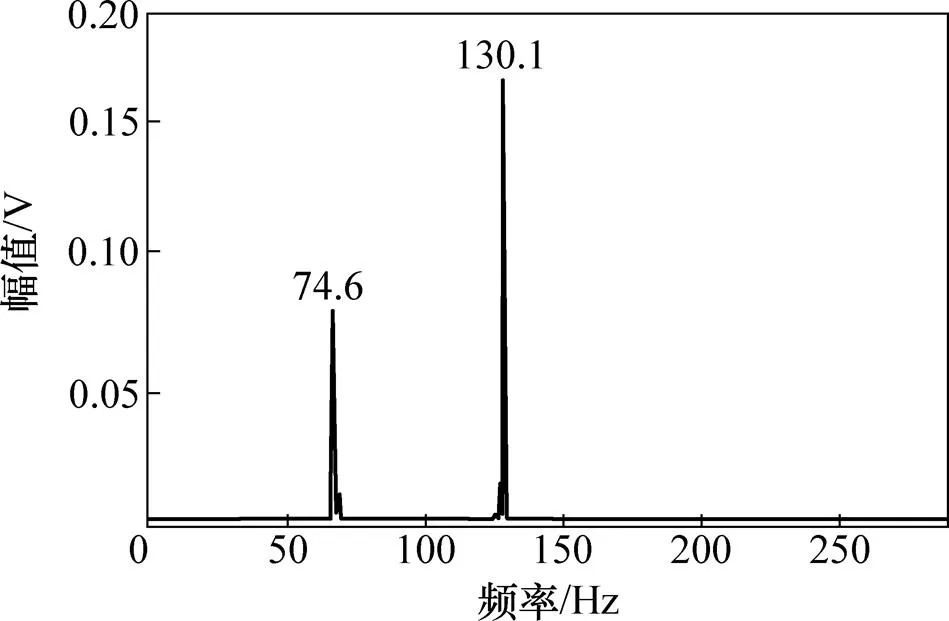
图15 实测信号的解调滤波频谱

图16 实测信号的包络频谱

4 结论

1) 根据轴承各个部分的故障特征系数和拟合转速计算IFCF趋势线，并根据各部分IFCF趋势线的拟合函数，构造对包络信号解调的相位函数。

2) 解调算法能够有效地将轴承各部分的IFCF的能量集中于初始频率，进而恢复其周期性，避免由于转速波动而造成频谱出现“频率模糊”现象。

3) 以IFCF的拟合函数的初始值为中心频率，构造巴特沃斯滤波器，可以提取轴承的故障特征频率，从包络信号滤除背景噪声和其他干扰成分，避免时域滤波时共振频率难以确定的问题。

4) 当轴承处于较强背景噪声时，时域滤波会出现轴承共振频带难以获取的问题，然而，在包络解调信号中滤波可以有效避免这一问题，为轴承故障诊断降噪提供新的研究思路。

[1] WANG Tianyang, LIANG M, LI Jianyong, et al. Bearing fault diagnosis under unknown variable speed via gear noise cancellation and rotational order sideband identification[J]. Mechanical Systems and Signal Processing. 2015, 62/63: 30−53.

[2] ZHAO Dezun, LI Jianyong, CHENG Weidong.Feature extraction of faulty rolling element bearing under variable rotational speed and gear interferences conditions[J]. Shock and Vibration,2015, 2015(3): 1−9.

[3] CHEN Jinglong, ZI Yanyang, HE Zhengjia, et al. Compound faults detection of rotating machinery using improved adaptive redundant lifting multiwavelet[J]. Mechanical Systems and Signal Processing, 2013, 38(1): 36−54.

[4] WANG Tianyang, LIANG M, LI Jianyong, et al. Rolling element bearing fault diagnosis via fault characteristic order (FCO) analysis[J]. Mechanical Systems and Signal Processing, 2014, 45(1): 139−153.

[5] 王晓冬, 何正嘉, 訾艳阳. 小波自适应构造方法及滚动轴承复合故障诊断研究[J]. 振动工程学报, 2010, 23(4): 438−444. WANG Xiaodong, HE Zhengjia, ZI Yanyang. Adaptive construction of multiwavelet and research on composite fault diagnosis of rolling bearing[J]. Journal of Vibration Engineering, 2010, 23(4): 438−444.

[6] 明安波, 褚福磊, 张炜. 滚动轴承复合故障特征分离的小波-频谱自相关方法[J]. 机械工程学报, 2013, 49(3): 80−87. MING Anbo, CHU Fulei, ZANG Wei. Compound fault features separation of rolling element bearing based on the wavelet decomposition and spectrum auto-correlation[J]. Journal of Mechanical Engineering, 2013, 49(3): 80−87.

[7] CHEN Guohua, QIE Longfei, ZHANG Aijun, et al. Improved CICA algorithm used for single channel compound fault diagnosis of rolling bearings[J]. Chinese Journal of Mechanical Engineering, 2016, 29(1): 204−211.

[8] 周俊，伍星, 迟毅林, 等. 盲解卷积和频域压缩感知在轴承复合故障声学诊断的应[J]. 机械工程学报, 2016, 52(3): 63−70. ZHOU Jun, WU Xing, CHI Yilin, et al. Blind deconvolution and frequency domain compressive sensing application in bearing composite acoustic fault diagnosis[J]. Journal of Mechanical Engineering, 2016, 52(3): 63−70.

[9] BONNARDOT F, BADAOUI M E, RANDALL R B, et al. Use of the acceleration signal of a gearbox in order to perform angular resampling (with limited speed fluctuation)[J]. Mechanical Systems and Signal Processing, 2005, 19(4): 766−785.

[10] 郭瑜, 秦树人. 无转速计旋转机械升降速振动信号零相位阶比跟踪滤波[J]. 机械工程学报, 2004, 40(3): 50−54. GUO Yu, QIN Shuren. Tacholess order tracking filtering for run-up or coast down vibration signal of rotating machinery based on zero-phase distortion digital filtering[J]. Chinese Journal of Mechanical Engineering, 2004, 40(3): 50−54.

[11] SAAVEDRA P N, RODRIGUEZ C G. Accurate assessment of computed order tracking[J]. Shock and Vibration, 2006, 13(1): 13−21.

[12] CHENG Weidong, GAO R X, WANG Jinjiang. Envelope deformation in computed order tracking and error in order analysis[J]. Mechanical Systems and Signal Processing, 2014, 48(1/2): 92−102.

[13] WANG Tiangyang, HAN Qinkai, CHU Fulei, et al. A new SKRgram based demodulation technique for planet bearing fault detection[J]. Journal of Sound and Vibration, 2016, 385(22): 330−349.

[14] CAI Guanghong. The processing of rotor startup signals based on empirical mode decomposition[J]. Mechanical Systems and Signal Processing, 2006, 20(1): 225−235.

[15] WU Zhaohua, HUANG N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1−41.

[16] YEH J R, SHIEH J S. Complementary ensemble empirical mode decomposition: A noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135−156.

[17] CHENG Junsheng, ZHANG Kang, YANG Yu. An order tracking technique for the gear fault diagnosis using local mean decomposition method[J]. Mechanism and Machine Theory, 2012, 55: 67−76.

[18] OLHEDE S, WALDEN A T. A generalized demodulation approach to time-frequency projections for multicomponent signals[J]. Proceedings of the Royal Society A, 2005, 461(2059): 2159−2179.

[19] ANTONI J, RANDALL R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rolling machines[J]. Mechanical Systems and Signal Processing, 2006, 20(2): 308−331.

(编辑 伍锦花)

Rolling bearing multi-fault diagnosis based on envelope demodulation filter algorithm

LIU Dongdong, CHENG Weidong, WEN Weigang, WAN Guangtong

(School of Mechanical Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, China)

Considering that erroneous judgment and false negative occur in bearing multi-fault diagnosis because of interaction between different faults, and that it is difficult to obtain resonance band filtering parameters under the condition of variable speed and load, the method of rolling bearing multi-fault diagnosis based on envelope demodulation filter algorithm was proposed. Firstly, according to fault characteristic frequency coefficient of each part of the bearing and polynomial fitting function of rotating speed, instantaneous fault characteristic frequency (IFCF) trend was calculated. Secondly, phase functions were constructed based on fitting functions of the obtained IFCF trends, and the envelope signal obtained by Hilbert transform was demodulated. Finally, filtered signal was obtained from the narrow band Butterworth band-pass filter in which the initial value of IFCFs was used as centre frequency, and then frequency spectrum of demodulation filtering signal was obtained by fast Fourier transform (FFT). The results show that the algorithm makes energy of IFCFs concentrate in the position of initial value, and band-pass filter can be used to extract demodulated fault information in envelope signal. The proposed method not only overcomes the “frequency ambiguity” phenomenon caused by the change of speed, but also avoids the difficulty of determining resonance band in time domain filtering. The effectiveness of the proposed method is validated by simulation and experimental results.

variable speed; rolling bearing; multi-fault diagnosis; demodulation algorithm; instantaneous fault characteristic frequency (IFCF); Butterworth band-pass filter

TH165

A

1672−7207(2018)04−0881−07

10.11817/j.issn.1672−7207.2018.04.015

2017−04−09；

2017−06−07

国家自然科学基金资助项目(51275030)；中央高校基本科研业务费专项资金资助项目(2016JBM051)(Project(51275030) supported by the National Natural Science Foundation of China; Project(2016JBM051) supported by the Fundamental Research Funds for the Central Universities)

程卫东，博士，教授，从事机械故障诊断与信号处理研究；E-mail：wdcheng@bjtu.edu.cn