分数阶混沌扩频通信系统的设计

王会海，孙克辉，贺少波



分数阶混沌扩频通信系统的设计

王会海，孙克辉，贺少波

(中南大学 物理与电子学院，湖南 长沙，410083)

为了提高扩频通信系统的性能，设计分数阶混沌扩频通信系统。采用Adomain分解算法求解分数阶简化Lorenz系统，推导分数阶系统迭代式，得到系统的数值解。对迭代值进行简单的二值量化，生成多组互不相关的混沌伪随机序列。将混沌伪随机序列作为扩频码应用于扩频通信系统。在不同信噪比时，分析不同扩频码对通信系统性能的影响。研究结果表明：基于分数阶简化Lorenz系统生成的伪随机序列更随机，均通过美国国家科学技术研究所(NIST)的统计测试套件(STS)测试，序列的生成速度快；与整数阶混沌系统相比，分数阶扩频系统具有更大的秘钥空间，具有更好的安全性；分数阶混沌扩频通信系统的性能优于Hénon映射、Chen系统、m序列及Gold序列的性能，并且具有更大的多址容量。

扩频通信；分数阶微积分；混沌

扩频通信技术具有保密性能好、抗干扰能力强、与传统通信系统共用频段而不互相干扰的优点，被广泛应用于军事和民用系统，是现代无线通信技术的热点技术之一。扩频通信技术中的扩频码性能与系统的抗干扰、抗噪声、抗截获、信息隐蔽等能力密切相关。作为扩频码的二元伪随机序列应该具有良好的随机性、有足够长的码周期和复杂度、满足要求的序列数足够多且易于产生和处理等特点。目前，人们常用的扩频码有m序列、Gold序列等，但存在扩频码数量少和保密性能差等不足。由于混沌信号具有初值敏感性、随机性和宽谱性等特点，用混沌系统可以产生数量较多的序列作为扩频码，并且它们具有很好的相关性和平衡性。早在1992年，HEIDARI-BATENI等[1]在直接扩频(direct-sequence spread spectrum，DS-SS)系统中应用了混沌伪随机序列，从此，人们开始在这方面不断地进行研究，采用各种离散混沌系统和整数阶连续混沌系统产生扩频码[2−4]，使扩频码的选择范围和性能都得到较大提高。但随着计算机技术的迅速发展，破解技术得到更加深入研究和使用，传统的整数阶和离散混沌系统生成的扩频序列慢慢显现出它的局限性，如复杂度低、易破译不足等[5−7]。为了提高扩频通信的安全性，需要研究性能更优的扩频码。分数阶微积分具有很多优点[8−10]，因而，分数阶混沌系统已成为混沌研究的热点[11−16]。WANG等[13−14]采用Adomian分解算法研究了分数阶简化Lorenz系统和分数阶Lorenz-Stenflo系统，发现随着系统微分阶数增加，系统的最大Lyapunov指数逐渐减小，即在系统为混沌的阶数范围内，分数阶混沌系统的越小，系统越复杂，分数阶混沌系统比对应的整数阶混沌系统更复杂。HE等[15−16]的研究也表明分数阶混沌系统的复杂度比整数阶混沌系统的复杂度更高。另外，基于Adomian分解算法在DSP平台实现了分数阶混沌系统，证明分数阶混沌系统的数字电路可实现，为分数阶混沌系统在扩频通信中的应用奠定了硬件基础[13−14]。为此，本文作者以分数阶简化Lorenz系统为例，设计基于分数阶混沌系统的扩频通信系统，并对混沌扩频通信系统进行仿真和性能测试分析。

1 分数阶简化Lorenz系统分析

分数阶简化Lorenz系统的方程为

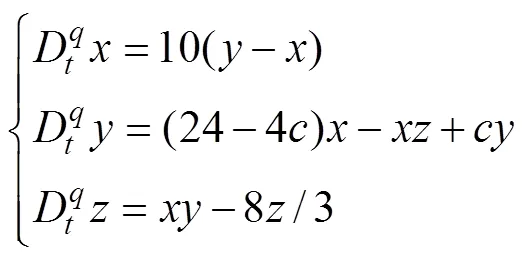
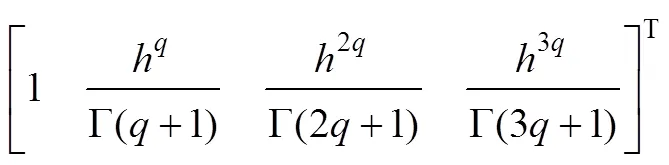
其中：h为迭代步长；为Gamma函数；

当=0时，[0，0，0]表示系统的初始状态。对于整数阶简化Lorenz系统，一般采用四阶龙格库塔法求解，得到其数值解的形式如下(其中，每次迭代包括59次加法和57次乘法)：

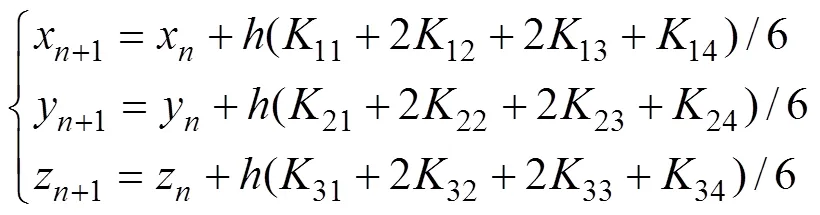
其中：

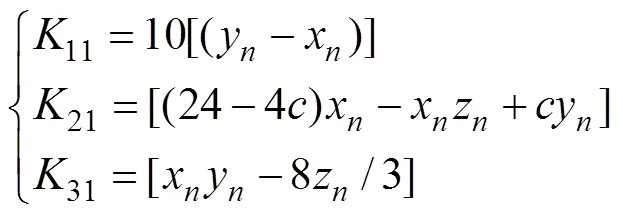
分数阶简化Lorenz系统和整数阶简化Lorenz系统的计算速度比较如表1所示。在迭代过程中进行的乘法和加法次数越多，表示迭代1次花费的时间越多，即速度越慢。所以，在同等条件下，分数阶简化Lorenz系统的计算速度比整数阶简化Lorenz系统的计算速度快。

表1 分数阶系统与整数阶系统计算速度对比

2 扩频码的生成与分析

根据图1，在式(2)~(6)中，取初始值[0，0，0]= [0.1，0.2，0.3]，=5，=0.65，=0.01，对应的分数阶简化Lorenz系统的最大Lyapunov指数为3.067 9，而采用四阶龙格库塔法求得的对应整数阶系统的最大Lyapunov指数为0.500 8，这说明在此条件下，分数阶简化Lorenz系统比整数阶简化Lorenz系统更复杂，更有利于产生用于扩频通信系统的扩频码。下面针对迭代过程中得到分数阶混沌序列，采用如图2所示的量化算法，设计伪随机序列发生器。

图2中，将每次迭代得到的混沌序列x+1，y+1和z+1均乘以1011，并取其整数部分，得到3个64位二进制整数(DB63-DB0)，分别定义为I，I和I；然后选择I的后8位(DB7-DB0)作为伪随机二进制序列的8位，随着迭代进行，得到一组足够长的二进制伪随机序列BS1。同时，计算I⊕I⊕I，取其最后8位作为另一个伪随机二进制序列BS2的8位。这样，可同时产生2组伪随机二进制序列。此量化算法简单，在实现过程中能节省系统资源。下面对产生的伪随机序列进行分析测试。

在众多伪随机序列的标准测试工具中，NIST(National Institute of Science and Technology)的STS(statistical test suite)是比较权威的测试方法[17]。对BS1和BS2分别进行NIST测试，测试结果分别如表2和表3所示。其中，有5个测试项目需要测试多次，每一项测试的测试结果和通过测试的比例为多次测试中的最小值。从表2和表3可见：基于分数阶简化Lorenz系统得到的2组伪随机二进制序列均通过了NIST的STS测试，具有良好的随机性能。

汉明距离(Hamming distance)是专门用于测试2个二进制序列间互相关性的参数。计算上述得到的2个伪随机二进制序列BS1和BS2的汉明距离(见表4)，以判断二者的互相关性。当序列长度选取不同值时，BS1和BS2的汉明距离均约为50%，说明上述生成的2个伪随机二进制序列是互不相关的。

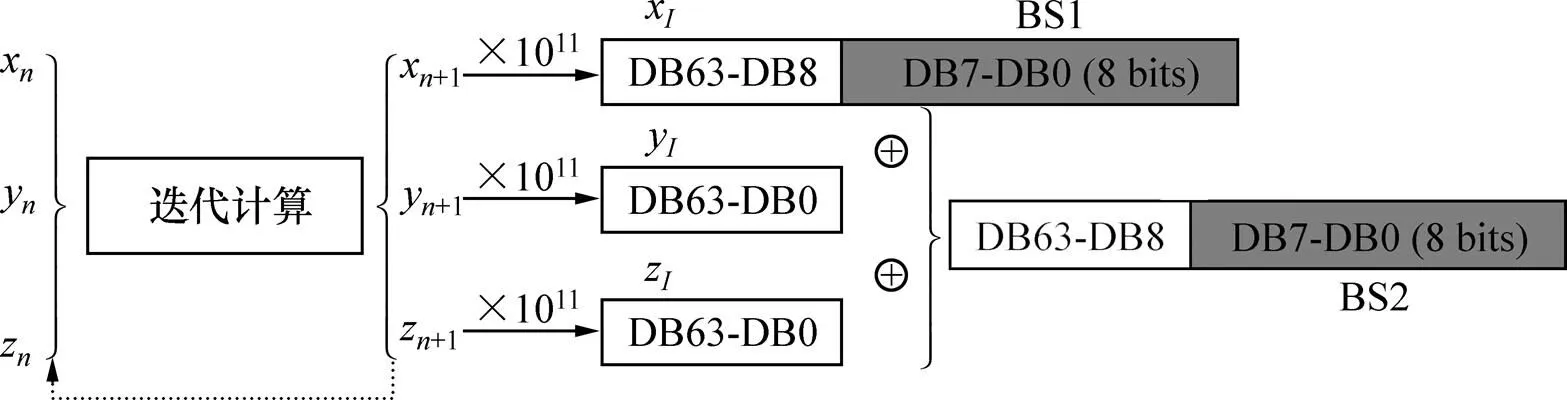
图2 伪随机序列发生器的二值量化算法

表2 BS1的NIST测试结果

表3 BS2的NIST测试结果

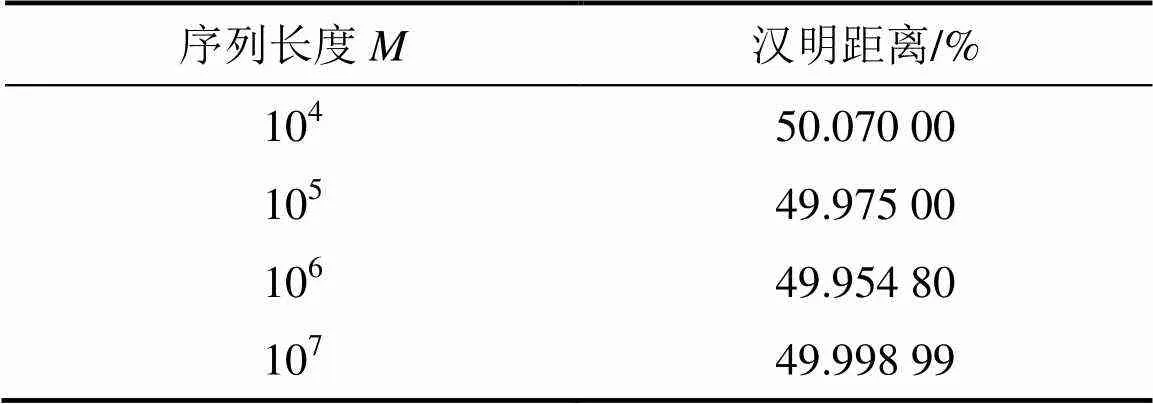
表4 不同长度的BS1与BS2的汉明距离

对于基于混沌系统的伪随机序列发生器，系统对初始值及系统参数的敏感性决定产生不同伪随机序列的数量。产生不同的伪随机序列对应的初始值和系统参数的取值范围，通常称其为伪随机序列发生器的“秘钥空间”。相对于整数阶混沌系统，在分数阶混沌系统中，是除了初始值和系统参数外另一个影响系统特性的分岔参数。这里重点研究的影响。从BS1中随机获取长度为107bit的二进制序列KS1，然后，仅改变，使=0.65+10−7，再从新的BS1中相同位置获取同样长度的二进制序列KS2，计算不同的KS1和KS2的汉明距离，所得结果如表5所示。从表5可见：考虑了阶数后，基于分数阶简化Lorenz系统产生的伪随机序列发生器秘钥空间至少增大107倍。

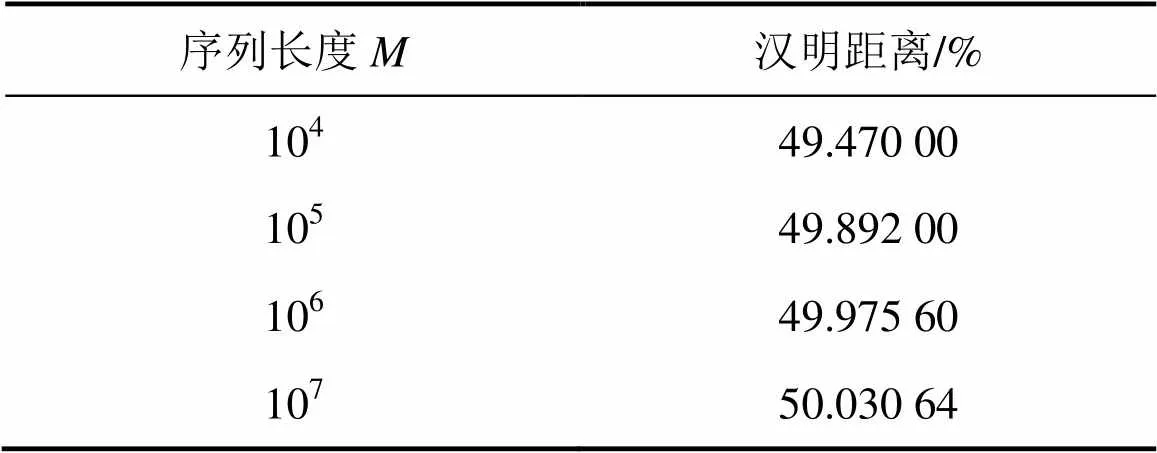
表5 不同长度的KS1与KS2的汉明距离

3 分数阶混沌扩频通信系统设计与性能测试

采用模块化设计方法，在Simulink平台设计分数阶混沌扩频通信系统。将伪随机序列按帧的格式生成扩频码。假设发送端与接收端已实现同步，故在接收端采用同样的扩频码用作扩频解调。为了检测不同信噪比(SN)时通信系统的性能，系统中信道的噪声可调。载波调制与解调方式使用BPSK(二进制相移键控)，最后，对接收的数据与发送的原始数据在误码率计算模块进行误码率分析。

从BS1中分别随机截取8，16和32 bit伪随机序列作为扩频码，测试中传输106位码元，得到误码率(BE)随信噪比SN的变化情况如图3所示。选择32 bit扩频码，当SN=−2 dB时，误码率接近0；选择8 bit扩频码，当SN=4 dB时，误码率才接近0；当扩频通信系统的SN不变时，扩频码的位数越多，则BE越小。可见：扩频码的位数对扩频通信系统的性能有很大的影响，位数越多，系统的性能越好。

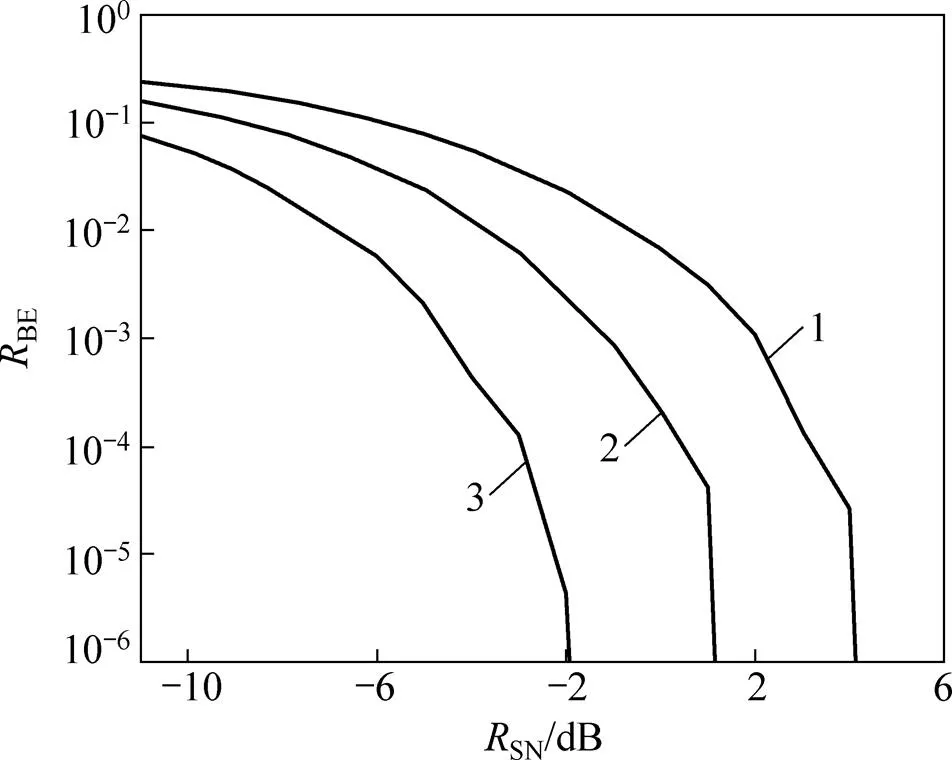
字节/bit：1—8；2—16；3—32。

在同样条件下，选择基于Hénon映射生成的伪随机序列(H序列)作为扩频码[18]，再选择基于Chen系统生成的伪随机序列(C序列)作为扩频码[19]，将上述分数阶混沌系统得到的伪随机序列记作FSL序列。在这3种情况下都选择32位扩频码，误码率随信噪比的变化如图4所示。从图4可见：当SN＜−5 dB时，这3种情况的误码率相近，都比较大，表明在恶劣的通信环境下，这3种情况的性能均不佳；当SN≥−4 dB时，基于FSL序列的误码率比另外2种情况的低；当SN=−2 dB时，基于FSL序列的误码率接近0，但其他2种情况下仍有较高的误码率；当SN≥−1 dB时，这3种情况的误码率都接近0。可见：基于分数阶简化Lorenz系统的扩频通信系统性能优于基于Hénon映射和Chen系统的扩频系统性能。

虽然用Gold序列和m序列作为扩频码时，其数量有限，但其通信系统的正确率较高。在同等条件下，都发送106位码元，基于FSL序列的伪随机序列与Glod序列和m序列用于扩频通信系统的性能对比如图5所示。从图5可见：当SN=−2 dB时，基于FSL序列的通信系统的误码率接近于0，明显小于Gold序列和m序列的误码率。可以说明基于分数阶混沌系统设计的伪随机序列性能优于Gold序列和m序列。

扩频通信技术的优点之一就是多个用户可以在同一个信道通信，互不干扰。增加通信系统的用户数量到4个，4个用户选择不同的初始条件，均截取32位伪随机序列作为扩频码，将4个用户的发送信号混合在一起发送出去，每个用户发送104个码元。通过分别检测每个用户的误码率随信噪比变化情况，所得结果如图6所示。从图6可见：4个用户中，每个用户的通信性能随信噪比的变化规律类似，在很低的信噪比下仍保持很低的误码率。这说明在同样的载波频率下，这4个用户虽然在同一信道，但由于扩频码的性能优良，其信号相互干扰很小。

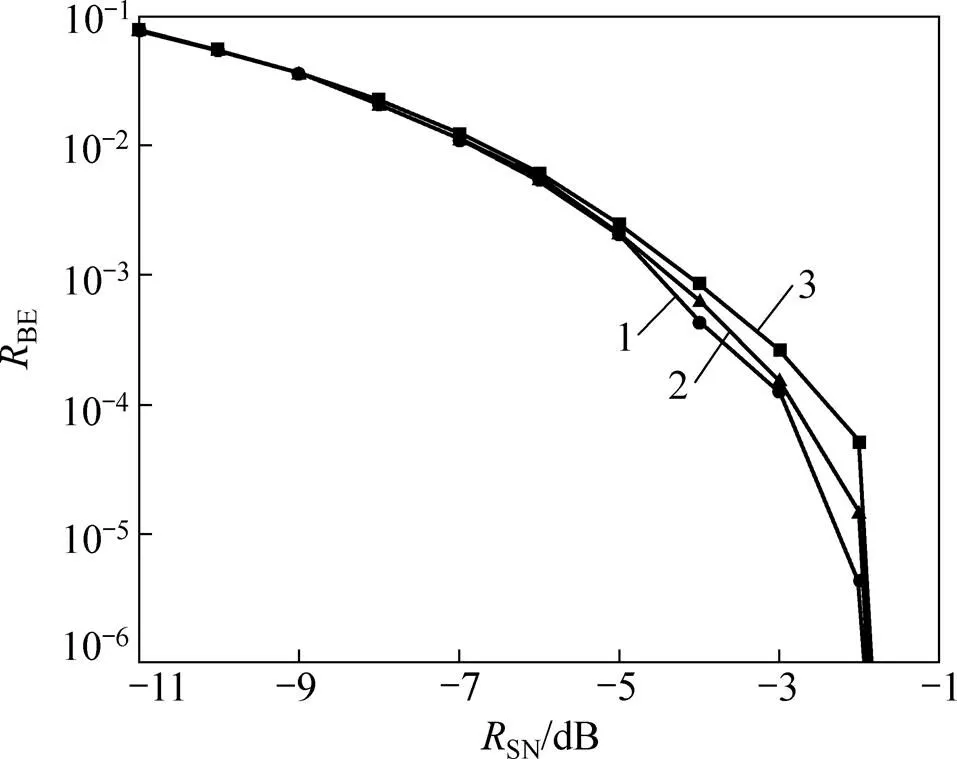
1—分数阶简化Lorenz系统；2—Hénon映射；3—Chen系统

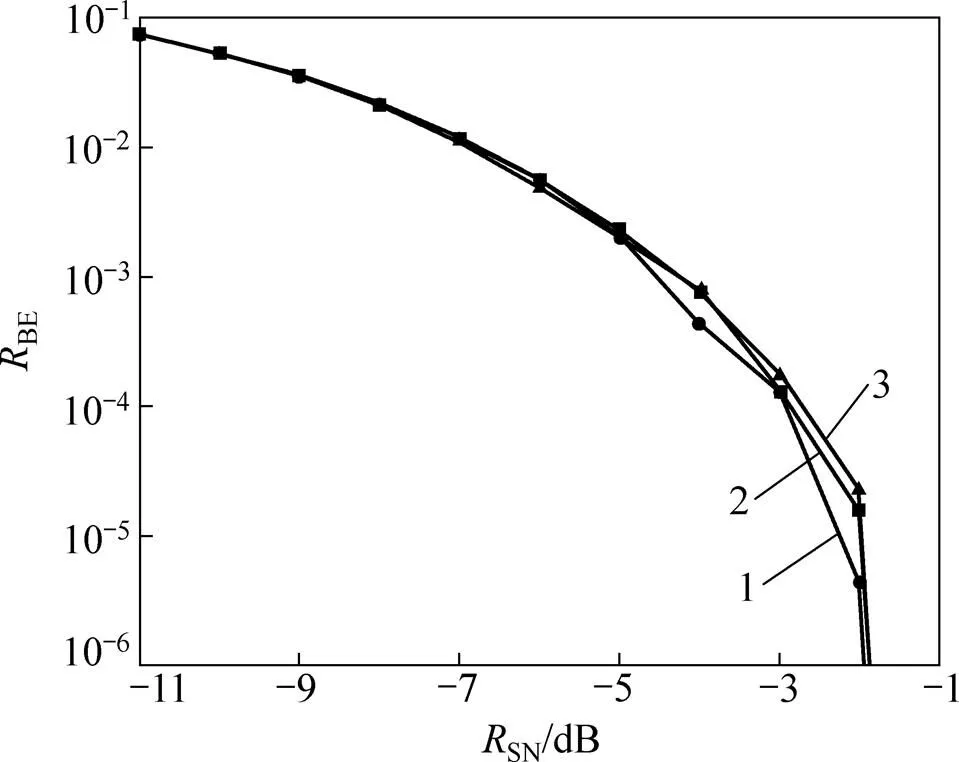
1—分数阶简化Lorenz系统；2—Gold序列；3—m序列。

改变多用户系统中的用户数量分别为2，4，6，8和10。为了比较用户数量对通信系统性能的影响，将每种情况下所有用户误码率取平均值，所得测试结果如图7所示。从图7可见：不同用户数量下的通信性能很接近，当SN≥−1 dB时，误码率均约接近于0。这说明使用的扩频码具有良好的正交性，系统具有较大的多址容量。

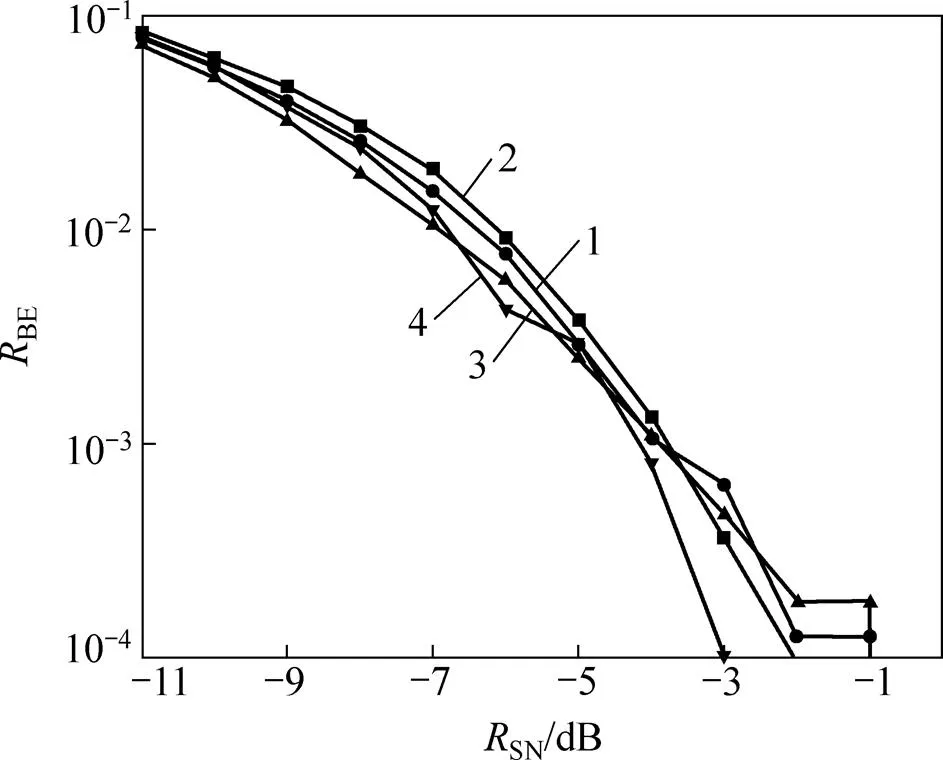
1—用户1；2—用户2；3—用户3；4—用户4。

用户数量/个：1—2；2—4；3—6；4—8；5—10。

4 结论

1) 分数阶简化Lorenz系统的计算速度比整数阶简化Lorenz系统快。

2) 分数阶简化Lorenz系统的秘钥空间比对应整数阶系统的秘钥空间约大107倍。

3) 在扩频通信系统中，基于分数阶混沌系统产生的伪随机序列性能优于基于Hénon映射和Chen系统产生的伪随机序列性能，也优于m序列及Gold序列性能，适合于设计扩频通信。

4) 分数阶混沌扩频通信系统具有更大的多址 容量。

[1] HEIDARI-BATENI G, MCGILLEM C D, TENORIO M F. A novel multiple-address digital communication system using chaotic signals[C]//IEEE International Conference on Communications Circuits and Systems (ICCCAS). Chicago, USA, 1992: 1232−1236.

[2] ROVATTI R, SETTI G, MAZZINI G. Chaotic complex spreading sequences for asynchronous DS-CDMA. Part II.Some theoretical performance bounds[J]. IEEE Transactions on Circuits & Systems Ⅰ, 1998, 45(4): 496−506.

[3] QI Aixue, HAN Chunyan, WANG Guangyi. Design and FPGA realization of a pseudo random sequence generator based on a switched chaos[C]//IEEE International Conference on Communications, Circuits and Systems (ICCCAS). Monterrey, USA, 2010: 417−420.

[4] LIU Liye, YAN Xiao, LUO Haoding, et al. A novel composite chaotic sequence for low voltage power line spread spectrum communication[C]//IEEE Power Engineering and Automation Conference (PEAM). Shanghai, China, 2012: 1−6.

[5] WANG Xingyuan, LIU Lingtao. Cryptanalysis and improvement of a digital image encryption method with chaotic map lattices[J]. Chinese Physica B, 2013, 22(5): 198−202.

[6] LI Chengqing, ZHANG Leoyu, OU Rong, et al. Breaking a novel colour image encryption algorithm based on chaos[J]. Nonlinear Dynamics, 2012, 70(4): 2383−2388.

[7] ZHU Congxu, XU Siyuan, HU Yuping, et al. Breaking a novel image encryption scheme based on Brownian motion and PWLCM chaotic system[J]. Nonlinear Dynamics, 2015, 79(2): 1511−1518.

[8] CHEN Xiaolong, GUAN Jian, LIU Ningbo, et al. Maneuvering target detection via radon-fractional Fourier transform-based long-time coherent integration[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 939−953.

[9] AROUDI A E, OUAKAD H, BENADERO L, et al. Analysis of bifurcation behavior of a piecewise linear vibrator with electromagnetic coupling for energy harvesting applications[J]. International Journal of Bifurcation & Chaos, 2014, 24(24): 1450066.

[10] ASLAM M S, RAJA M A Z. A new adaptive strategy to improve online secondary path modeling in active noise control systems using fractional signal processing approach[J]. Signal Processing, 2015, 107(4): 433−443.

[11] KHAN M, SHAH T. An efficient construction of substitution box with fractional chaotic system[J]. Signal Image & Video Processing, 2015, 9(6): 1335−1338.

[12] HU Jianbing, LU Guoping, ZHAO Lingdong. Synchronization of fractional chaotic complex networks with distributed delays[J]. Nonlinear Dynamics, 2016, 83(1/2): 1101−1108.

[13] WANG Huihai, SUN Kehui, HE Shaobo. Dynamic analysis and implementation of a digital signal processor of a fractional-order Lorenz-Stenflo system based on the Adomian decomposition method[J]. Physica Scripta, 2015, 90(1): 015206.

[14] WANG Huihai, SUN Kehui, HE Shaobo. Characteristic analysis and DSP realization of fractional-order simplified Lorenz system based on Adomian decomposition method[J]. International Journal of Bifurcation & Chaos, 2015, 25(6): 1550085.

[15] HE Shaobo, SUN Kehui, WANG Huihai. Multivariate permutation entropy and its application for complexity analysis of chaotic systems[J]. Physica A Statistical Mechanics & Its Applications, 2016, 461: 812−823.

[16] 贺少波, 孙克辉, 王会海. 分数阶混沌系统的Adomian分解法求解及其复杂性分析[J]. 物理学报, 2014, 63(3): 030502.HE Shaobo, SUN Kehui, WANG Huihai. Solution of the fractional-order chaotic system based on Adomian decomposition algorithm and its complexity analysis[J]. Acta Physica Sinica, 2014, 63(3): 030502.

[17] OLVER F W, LOZIER D W, BOISVERT R F, et al. NIST handbook of mathematical functions[M]. London, England: Cambridge University Press, 2010: 1−30.

[18] 李家标, 曾以成, 陈仕必, 等. 改进型Hénon映射生成混沌伪随机序列及性能分析[J]. 物理学报, 2011, 60(6): 60508. LI Jiabiao, ZENG Yicheng, CHEN Shibi, et al. Modified Hénon map generated chaotic pseudorandom-bit sequences and performance analysis[J]. Acta Physica Sinica, 2011, 60(6): 60508.

[19] HU Hanping, LIU Lingfeng, DING Naida. Pseudorandom sequence generator based on the Chen chaotic system[J]. Computer Physics Communications, 2013, 184(3): 765−768.

(编辑 陈灿华)

Design of communication system of fractional-order chaotic spread spectrum

WANG Huihai, SUN Kehui, HE Shaobo

(School of Physics and Electronics, Central South University, Changsha 410083, China)

In order to improve the performance of the spread spectrum communication system, a fractional-order chaotic spread spectrum communication system was designed. The fractional-order simplified Lorenz system was solved by adopting Adomian decomposition method. The iteration of the fractional-order system was deduced, and the numerical solution was obtained. Several uncorrelated chaotic pseudo-random sequences were generated by a simple binaryzation algorithm for iterative results. The pseudo-random sequence was used as spread spectrum code in spread spectrum communication system. At different signal-to-noise ratios, the influence of different spread spectrum codes on the performance of the communication system was analyzed. The results show that the pseudo-random sequences based on the fractional-order simplified Lorenz system have good randomness, and all pass statistical test suite(STS) of National Institute of Science and Technology(NIST).The generation of these pseudo-random sequences is fast. They have bigger secret key space and better security than the integer-order counterpart. The performance of the spread spectrum communication system designed is better than that of Hénon map, Chen system, m-sequence and Gold sequence, and has a good multiple access capability.

spread spectrum communication; fractional calculus; chaos

TN918.91

A

1672−7207(2018)04−0874−07

10.11817/j.issn.1672−7207.2018.04.014

2017−06−29；

2017−08−22

国家自然科学基金资助项目(61161006，61573383，61502538)(Projects(61161006, 61573383, 61502538) supported by the National Natural Science Foundation of China)

孙克辉，博士，教授，从事混沌理论与应用研究；E-mail：kehui@csu.edu.cn