现代教育理念与教学设计

李春光

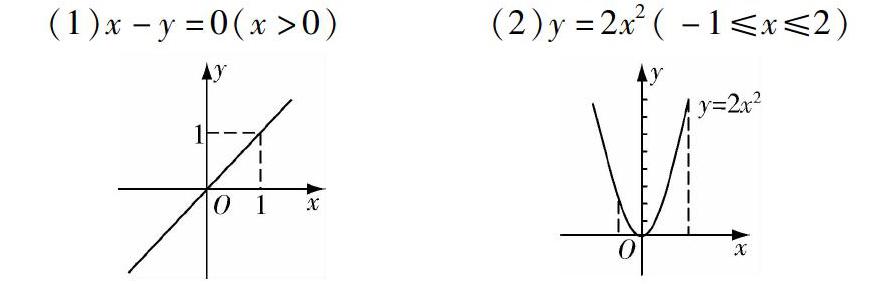
【摘要】数学教学应该着眼于让学生经历数学探索活动的过程.按照概念形成的学习模式对曲线与方程进行教学设计，强调问题设计应突出概念的本质，应树立“产生需要，形成体验，获得发展”的基本教学理念，重视学生的数学精神、思想和方法的形成.

【关键词】教学设计；过程；体验；思想

“曲线与方程”的概念，从理论上揭示了几何中的“形”与代数中的“数”的统一.曲线和方程建立了对应关系以后，曲线的很多性质可以反映在方程上，方程的某些性质又反映在曲线上.笔者结合“曲线与方程”的教学设计，着眼于让学生经历数学探索活动的过程，强调学生的探索经历和得出新发现的体验.

在进行“曲线与方程”的教学之前，学生已经学习了直线的方程，对于直线和方程之间的对应关系有了一种初步的认识.“曲线与方程”的教学在已有知识基础上，从理论上提高了对曲线和方程关系的认识，定义了“方程的曲线”和“曲线的方程”.本节课是采用“概念形成”的概念学习方式来设计“曲线与方程”的教学，以“曲线与方程”的教学内容作为载体，以知识的建构、发展学生思维和认识能力为目标，通过教师创造性地设置教学情境来展示知识的形成，突出学生主动学习和再创造过程.

一、“曲线与方程”的教学设计

（一）引例（课题的提出）

（1）画出两坐标轴所成的角在第一、三象限的平分线L，并写出其方程.

（2）画出函数y=2x2的图像C.

思考、讨论：符合某种条件的点的集合L和C分别与其方程是怎样地联系起来的？

用几何画板设计直线和方程、抛物线和方程的动态变化的关系，向学生展示直线和方程、抛物线和方程的动态变化，让学生充分观察并组织讨论，对曲线上不同的点对应的坐标和方程的解关系得到充分感知，获得丰富的表象和信息，产生众多的联想.由此引导、启发学生得出结论：（1）直线上的点与二元一次方程的解有如下的关系：直线上点的坐标都是这个方程的解，以方程的解为坐标的点都是这条直线上的点；（2）抛物线上的点与二元二次方程的解有如下的关系：抛物线上点的坐标都是这个方程的解，以方程的解为坐标的点都是这条抛物线上的点.

（二）运用反例，揭示内涵

下述方程分别表示所对应图上的曲线吗？为什么？

（1）x-y=0（x>0） （2）y=2x2（-1≤x≤2）

学生通过对一些反例的观察和讨论，进一步理解本节课问题的实质性内涵，通过以上两步教学，学生对于曲线的方程和方程的曲线的概念的本质已基本上了然于心.曲线的方程和方程的曲线的概念的得出已是水到渠成.但是，不要把概念过早地“符号化”，要延长知识的发生与发展的过程，要学生充分经历过程，以使学生达到对概念的真正理解.

（三）启发学生讨论、归纳，得出定义

直角坐标系中，如果某曲线C上的点与一个二元方程f（x，y）=0的实数解建立了如下的关系：

（1）曲线上的点的坐标都是这个方程的解.（一点不多——纯粹性）

（2）以这个方程的解为坐标的点都是曲线上的点.（一点不少——完备性）

那么，这个方程叫作曲线的方程，这条曲线叫作方程的曲线.

在观察以上几个曲线与方程的关系正例和反例的基础上，启发学生讨论、归纳，得出定义，这种启发，是以探索“曲线与方程的等价关系”为载体，启发学生提出问题、分析和研究问题；启发学生寻找曲线与方程的关系；启发学生提出对“曲线与方程”的关系的猜想：曲线上的点集与方程的解集是一一对应关系.

对本质意义的认识逐步分化，不断综合贯通.教学时要多举实例，增加变式思维训练，尽可能形象说明定义中两个条件的含义，强化和深入理解“一点不多”和“一点不少”缺一不可，要注重淡化形式，重在实质，对于究竟是不满足“纯粹性”还是不满足“完备性”不必追究，关键是“缺不缺”，缺哪一个都不行.当然，这个过程并不是在这一节课里就能全部解决的，更多的是需要个人的体验和感悟，因而，需要在后继教学中，继续对概念的同化过程，不断加深学生对定义的理解.

二、对课堂教学设计的思考

数学学习应该是一个体验和探索的过程.對于数学教学而言，学什么和怎样学同样重要，甚至有时过程更重于知识.课堂教学设计应树立“产生需要形成体验获得发展”的基本理念，引导学生充分经历数学知识的形成过程.学生通过这一过程，理解一个问题是怎样提出来的，一个数学概念是怎样形成的，一个数学结论是怎样获得的.这样学生的数学学习不再是单一的、枯燥的，以被动听讲和练习为主的方式，它是一个生动活泼的、主动的和富有个性的充满生命力的过程.在亲身体验和探索中认识和学习数学，解决问题，理解和掌握基本的数学知识、技能和方法.这是学生生存、成长、发展创造所必须经历的过程，它留给学生的是一些对他们终身学习和发展有用的数学的精神、思想和方法.