振动加速度信号时域和频域积分方法研究

周华

（航空工业直升机所，江西景德镇 333001）

0 引 言

振动是直升机的永恒话题，振动问题相比固定翼飞机更为突出。直升机的振动特性是由若干定频和随机宽频背景噪声信号叠加而成。飞机上不同部件对振动的判断标准不一，例如传动系统转动部件一般以振动速度作为判据；发动机则通常在不同频段内分别以振动加速度、振动速度、振动位移进行规定；驾驶舱、操纵线系等机体部位同样也以3种振动参数进行分别规定。

在实际测试中，鉴于传感器大小、重量、测试成本、传感器安装环境等条件限制，大多数情况不可能同时测量振动加速度、速度和位移3种参数。由于微分处理的近似方法误差较大，且加速度传感器通常体积小、重量轻、灵敏度高、有效频带宽等优点，除了一些对振动位移或速度有明确规定的部位，加速度传感器在振动测试中应用更为普遍。

振动加速度转换为速度或位移，一般可在时域或频域内进行积分处理。需要注意的是，由于测试仪器温度变化等原因，加速度信号中不可避免存在零点漂移、趋势项等特征，若进行二次积分生成位移，则又会产生新的趋势项和直流量。

假设加速度信号为a（t），速度积分公式为

其中，C为常数项。

位移积分公式为:

式中：Ct为一次积分后的直流分量产生的新的一次趋势项；D为新的直流分量。如何正确消除趋势项和直流分量等的影响，对积分的精度影响很大。

本文给出时域和频域内振动加速度和速度、位移转换较为实用的方法，并在时域内对两种积分方法进行对比验证，且验证了积分结果的频域特性，对提高振动信号处理分析能力起到较大的推动作用。

1 时域内积分处理方法

以往的时域积分方法多是基于离散信号的累计梯形法则（线性）、辛普森法则（二次抛物线）等的数值求积，然后控制截断误差，保证求积的收敛性即可。

然而由于每一次积分后，都会出现新的趋势项和直流量，低频趋势项对积分的结果影响很大，二次积分后往往信号可能会畸变甚至完全失真。另外，时域内去趋势项也会造成信号能量的损失。因此，传统的时域数字积分精度往往较低。

比较可行的时域内积分方法如下：

在积分之前，若加速度信号中有明显的直流、高频随机噪声等，应先进行处理。例如用五点三次平滑法对时域信号作平滑前处理。

首先用辛普森（或梯形等）法则进行积分，速度和位移计算公式如下：

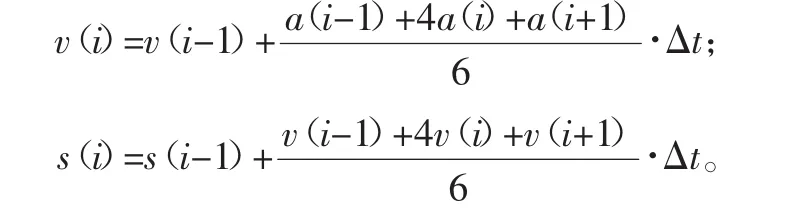
式中：i=0,1，…N-1；Δt为采样时间，当i-1＜0时，该点值为0。

计算速度和位移积分能量Venergy和Senergy：

将速度或位移积分结果用减均值或多项式最小二乘法去除趋势项：

到式（9）为止，速度积分已完成。对于位移积分，除了进行去趋势项处理外，还需进行去除高次项处理。

高次项可用多项式拟合法来进行去除，即根据时域曲线运用Gauss计算拟合得到多项式系数：

式中：n为多项式次数（一般用2次即可），［b0,b1,...,bn］为拟合后的多项式系数，X为时间轴。

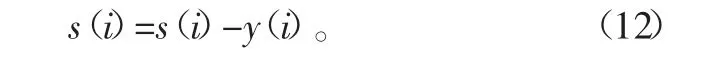
式（9）和式（12）即是去除高次项后最终速度和位移积分结果。

2 频域内积分处理方法

频域内积分是将信号由时域转换到频域内进行处理，即可操作上避免时域内多次积分需多次去趋势项的繁琐，也可避免去趋势项造成能量损失的累计误差。时域与频域之间转换采用快速傅里叶变换。傅里叶变换的积分定理为

由式（13）可知，当ω＜1，即f＜1/2π时，信号会放大，因此在不需要的频段可人为置零，即人为进行低频滤波。

进行FFT变换后，为方便处理，将零频点（直流分量）移至频谱的中间，使经过FFT得到的实部和虚部数据与频率对应起来，变成我们常见的频谱图排序。

由上面两式可知，速度和加速度相位相差90°，位移和加速度相位相差180°。

完成上述步骤后，将零频点移至频谱的起始位置，以与FFT结果一致，最后再进行FFT逆变换得到时域量值。需要注意的是，速度积分完成后，仍需按式（5）进行去趋势项处理。位移积分做完频域内积分，除了去趋势项处理外，也需进行式（11）和式（12）所示的去除高次项处理。

3 实例验证

3.1 时域和频域积分的符合性验证

以某部件振动台数据为例。在额定工作状态，特征振频是固定的。典型的振动加速度信号如图1所示。

根据第1节和第2节的内容，分别进行时域和频域内积分，两种积分的结果对比情况见图2和图3。

图1 典型振动信号时域特征

图2 时域和频域内速度积分

图3 时域和频域内位移积分

由图2和图3可知，时域和频域内积分结果一致性较好。

3.2 积分结果的频域特性验证

取某段振动数据为例，其时域和频域特性见图4。含有2个主频，5.25 Hz（加速度1.0g）、47.25 Hz（加速度2.0g）。

将其进行积分，速度和位移积分结果见图5和图6。

将积分结果进行FFT分析，结果见图7和图8。

可以用如下公式对速度和位移的量值进行简单评估：

图4 典型振动曲线

图5 速度积分结果

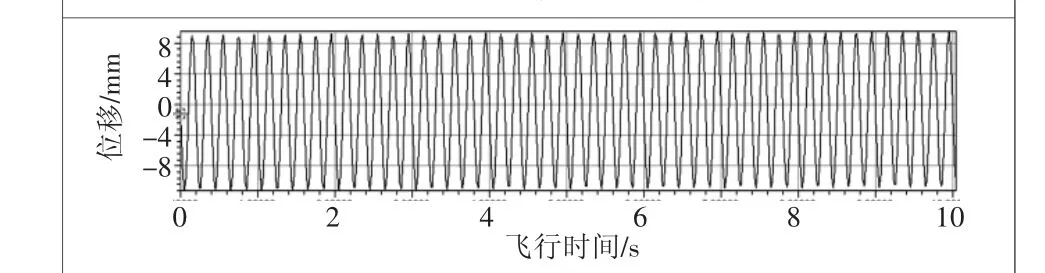
图6 位移积分结果

表1 理论值和积分结果对比

图7 速度积分FFT结果

图8 位移积分FFT结果

理论和实际积分结果对比见表1。

由表1可知，积分结果符合性较好，低频段符合性比高频段要稍差，但误差也在10%以内，满足实际工程需求。

4 结论

本文所述的时域和频域积分方法，两者在时域相似性以及频谱特性方面，都有较好的效果，可以用于实际工程应用。

[参考文献]

[1] 冯康.数值计算方法[M].北京:国防工业出版社,1978.

[2] 王济,胡晓.MATLAB在振动信号处理中的应用[M].北京:中国水利水电出版社,2006.

[3] 李智勇.基于频域积分的振动信号处理方法[J].汽车科技,2009(5):28-30.

[4] 徐庆华.试采用FFT方法实现加速度、速度与位移的相互转换[J].振动、测试与诊断,1997(4):30-34.