一种新型矩形密封槽设计

2018-05-16王利鸣荆晓兵陈楠高峰戴曼戴文华

机械工程师 2018年4期

王利鸣，荆晓兵，陈楠，高峰，戴曼，戴文华

（中国工程物理研究院a.流体物理研究所；b.脉冲功率重点实验室，四川绵阳 621999）

0 引言

在加速器及其他大型物理实验装置的设计、安装和维护过程中，通常要涉及到大量的不同形式、不同结构的密封设计及密封件的选取[1-10]。其中矩形密封槽和密封圈的匹配是密封设计中的关键性问题之一。因此，如何在设计中提高工作效率，同时保证达到长期稳定的可靠密封要求；如何选用标准化的密封件并且可具备互换性，便于维护，是非常值得探讨的问题[11-13]。

1 问题的提出

图1所示为一个国标O形密封圈，如果密封圈尺寸的选取和矩形密封槽的结构设计不匹配，会引起一系列的问题：

1）如果选取的密封圈内径d1、截面直径d2与密封槽的结构设计不匹配，会导致密封圈变形、表皮破损，压缩量不足等因素，进而影响到长期稳定可靠的密封性能。

2）密封槽截面设计与O形密封圈截面直径d2不匹配它就不可能形成长期稳定的可靠密封,密封圈会产生塑性变形，严重时造成密封圈的表皮破损,而影响到使用寿命；如果压缩量不足，也达不到密封的效果。

3）如果选取的密封件不是国标而是非标，就会给后续的工作带来一系列麻烦和困难，如需要制作模具、提高加工费用、延长加工周期、造成维护困难。

4）如密封圈老化、变形已无法满足实验所需要的密封要求，在更换时，如果是非标就很难在市场上买到所需要的密封件，给后续的维护工作带来麻烦。

因此，在大型复杂系统密封结构设计中应首先按照标准化、系列化的原则对密封圈的尺寸进行选取，只有这样才能实现制造与维护方便的效果。

在《真空设计手册》中使用下述公式计算密封槽的深度和宽度[14]：

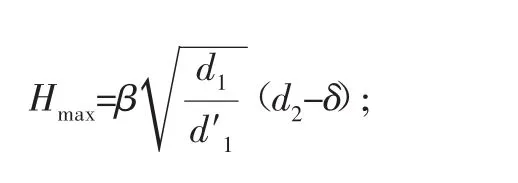
图1 密封圈内径d1、截面直径d2

式中：H为密封槽深度；C为密封槽宽度；d1为自由状态下密封圈内直径；d′1为受力状态下密封圈内直径；β为密封槽深度系数；ρ为密封槽宽度系数；d2为密封圈截面直径；δ为密封圈截面直径公差。

公式较为复杂，相关参数获取困难，工程设计中较难应用。而在《机械设计手册》中还没有查到有关矩形密封结构的设计计算公式[15]。在实际工作中大多数都是凭自己的工作经验来设计矩形密封槽结构及密封件的选取。因此，设计一种规范、简便、有效的具有实际工作意义的矩形密封槽设计方法是非常有必要的。

2 密封圈与密封槽的匹配关系

在设计矩形密封槽时，应首先考虑矩形密封槽和密封圈的匹配关系，所以设计时须要满足以下4个方面的基本原则：

1）由于O形密封圈位于矩形密封槽中受到密封槽宽度的限制时，密封的压力会随着压缩量的增加而急剧增加。设计密封槽时，除考虑O形密封圈公差的影响外，还需要考虑O形密封圈装配在密封槽中，O形密封圈截面直径d2伸展的影响。经验证明，密封圈材料为普通橡胶时，密封的压力取1.3 MPa左右比较适宜[14]。

2）因为密封圈具有受力后形状发生改变而保持体积不变的性质，即不可压缩的弹性变形能力。超过弹性压缩极限密封圈就会产生塑性变形，严重时造成表皮破损。相对于密封槽，密封圈截面直径d2尺寸过小，压缩量不足，不能形成长期稳定的可靠密封；过大会导致密封圈变形、表皮破损，而影响密封圈的使用寿命。

研究成果可以为森林资源评价、管理、统一确权登记提供数据支撑，为快速、大范围估测森林蓄积量提供技术支持，为自然资源空间数据库建设提供基础数据，还可应用于森林资源资产负债表编制与领导干部自然资源资产离任审计工作等。

3）由于安装在密封槽里的密封圈受压后形状发生变化而体积不变，因此密封槽要有容纳密封圈变形的空间。在受压密封状态下，密封圈不可能将密封槽完全充满，而且在不同的介质和温度下，密封圈会出现一定的膨胀，因此密封槽容积应有相对的余量。

4）在设计时应注意使密封槽的体积大于密封圈的体积，以免装配后裸露出密封圈，会形成较大的放气源，影响真空度的快速提升和真空度的稳定性，如图2所示。

因此，密封槽要有容纳密封圈变形的空间，而确保密封圈最适宜的压缩量是矩形密封槽设计中非常重要的参数之一。

3 参数的分析

3.1 密封槽的截面面积

矩形密封槽的截面面积如果小于密封圈的截面面积，那么，2个法兰表面就压不到一起，如果使用这种密封结构的法兰设计连接，加上连接螺栓拧得过紧，密封圈就会产生永久性变形甚至被压坏而影响到密封的性能。当安装在矩形密封槽中的密封圈截面形状近似为椭圆形、且与矩形密封槽相切时，如果密封槽截面积大于该椭圆外接长方形面积时，密封圈存在自由面，密封效果较差，所以允许的最大密封槽截面积为该椭圆外接长方形的面积。通过上述分析可以得到密封槽截面面积的选择范围：

式中：Aring为密封圈截面积；Agroove为密封槽截面积；Aellipse为椭圆面积；Arectangle为椭圆外接长方形面积。

进一步，在不损坏密封圈的前提下，为了获得较好的密封效果，应选择密封槽截面面积接近密封圈截面面积的设计。

3.2 密封槽的深度

由于密封圈具有受力后形状改变而保持体积不变，即不可压缩的弹性形变能力，所以，通常取密封圈的变形率为15%～30%[14]。因此密封槽深度的选取范围如下：

式中：H为密封槽深度；d2为密封圈截面直径。

通常情况下，真空密封应要求密封圈具有尽可能大的形变量，而普通机械密封对密封圈形变量的要求则较低。所以建议密封槽的深度选取原则：真空密封，密封槽的深度为0.7倍密封圈截面直径，即H=0.7d2；而对于普通机械密封，密封槽的深度可以取0.8倍密封圈截面直径。

3.3 密封槽的宽度

密封槽的宽度等于密封槽的截面面积除以密封槽的深度。由密封槽截面面积及密封槽深度的选择范围可以得到最大、最小密封槽宽度计算公式：

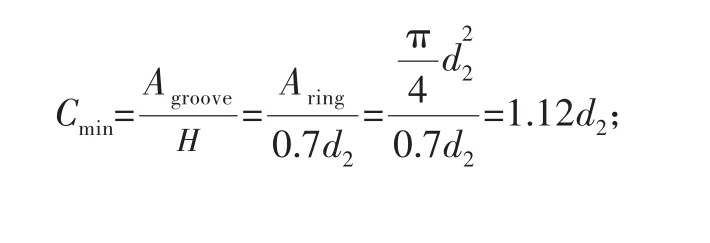
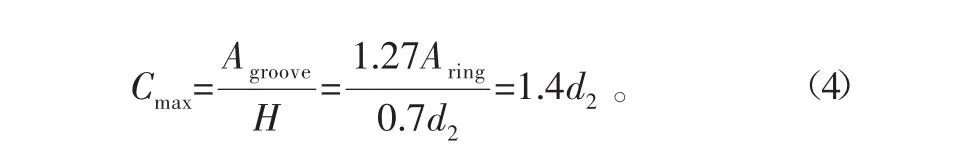
式中：Cmin为最小密封槽宽度；Cmax为最大密封槽宽度；Aring为密封圈截面积；Agroove为密封槽截面积；H为密封槽深度；d2为密封圈截面直径。

密封槽宽度的取值范围在密封圈截面直径的1.12～1.4倍之间。

因此，在不损坏密封圈的前提下，为了获得较好的密封效果，应选择密封槽的宽度近似为1.12倍密封圈的截面直径，即C=1.12d2。

基于前述对密封圈与密封槽匹配关系概念的理解，以及对密封槽截面面积、密封槽深度和密封槽宽度的参数分析，可以总结出如下简便、易行、有效的矩形密封槽深度、宽度计算公式：

式中：H为密封槽深度；C为密封槽宽度；d2为密封圈截面直径。

其中式（5）为真空矩形密封结构的设计计算公式，式（6）为普通机械矩形密封结构的设计计算公式。4 密封槽深度、宽度的总结设计算例

在实际设计中则要根据法兰盘的直径设计和法兰盘中的结构设计来选取确定国标真空密封圈的内径d1和密封圈的截面直径d2。

用公式（5）具体说明真空密封结构设计中矩形密封槽深度和宽度简便、有效的设计计算方法。

如图3所示，其法兰盘的直径设计为φ=205 mm，同时根据法兰盘中的其他结构设计，选取真空密封圈的内径d1=145 mm、密封圈的截面直径d2=5.3 mm（国标）。则根据式（5）可以非常简便地计算出密封槽的深度和密封槽宽度的密封结构设计结果，即：H=0.7×5.3=3.71 mm，C=1.12×5.3=5.94 mm。

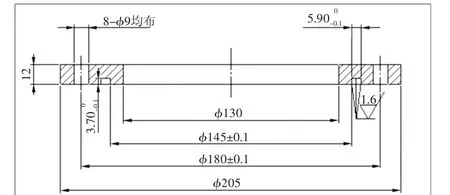
图3 计算实例-密封槽法兰面示意图

5 结语

通过对矩形密封结构设计中经常遇到的问题进行参数分析和结构尺寸计算，总结出一套具有实际工作意义的矩形密封槽的结构设计方法。该方法在“神龙一号”加速器、“神龙二号”加速器等大型复杂系统

的矩形密封结构设计中进行了大量成功的工程应用，结果表明，该矩形密封结构设计方法具有简便、易行、有效的特点。

通过分析矩形密封槽的设计过程，可以发现在矩形密封结构设计中密封圈的尺寸选取占据了更为基本和先决性的位置。大量的工程实施经验表明，在密封结构设计中应首先按照标准化、系列化的原则对密封圈的尺寸进行选取（尽量采用国标尺寸），只有这样才能实现制造与维护方便的效果。总之，有效的密封结构设计应建立在密封圈和密封槽同时合理选取、设计的基础之上。

[参考文献]

[1]丁伯南,邓建军,王华岑.“神龙一号”直线感应电子加速器[J].高能物理与核物理,2005(6):604-610.

[2] 石金水,邓建军,章林文.神龙二号加速器及其关键技术[J].强激光与粒子束,2016(1):1-8.

[3]李劲,张开志,代志勇.“神龙一号”加速器调试[J].中国物理C,2008(增刊1):247-249.

[4]代志勇,张开志,文龙.“神龙一号”直线感应加速器多功能腔设计[J].强激光与粒子束,2004(10):1334-1336.

[5]代志勇,章文卫,谢宇彤.“神龙一号”加速器束流输运系统研制[J].高能物理与核物理,2007(4):395-399.

[6]丁伯南,张开志,文龙.“神龙一号”注入器研制[J].高能物理与核物理,2005(3):219-223.

[7] 邓建军.直线感应电子加速器[M].北京:国防工业出版社,2006.

[8] 李洪,刘云龙,章林文.直线感应加速器机械轴精密对中方法[J].强激光与粒子束,2004(10):1349-1352.

[9] 达道安,姜万顺.加速器中的真空技术[J].真空与低温,1984(2):21-33.

[10] 李继和.机械密封技术[M].北京:化学工业出版社,1988.

[11] 关文锦,杜群贵.真空环境中O形密封圈泄漏分析[J].机械设计与制造,2013(4):66-69.