不同磁场环境下Heisenberg XXZ自旋系统中的热纠缠研究
2018-05-16闫丽
闫 丽
(菏泽学院 物理与电子工程系,山东 菏泽 274015)
量子纠缠作为量子计算和量子信息的核心资源,在量子隐形传态、量子密钥分配、量子密集编码等方面,尤其在量子信息处理过程中扮演着非常重要的角色[1-4].近几年,人们在J-C模型,T-C模型,Heisenberg自旋链模型中实现最大纠缠方面进行深入的研究,其中较简单的Heisenberg自旋链模型,如各向同性XX模型,XXX模型,各向异性XY模型、以及各向异性XYZ模型等等,因其广泛的应用前景更成为了人们关注的重点[5-9].随后,人们进行大量研究发现除了Heisenberg自旋链中的各向异性会对系统的量子纠缠产生重大影响以外,磁场的均匀、温度的高低、系统的各向异性、以及消相干的效应也是影响量子纠缠大小的重要因素,因此可通过操控这些参数的变化来获得有效的量子纠缠资源.Qiu等人在两比特Heisenberg XXX模型下研究了温度、Dzyaloshinskii-Moriya (DM)相互作用和耦合系数对系统的热纠缠影响[10].Cai等人在两比特Heisenberg XXZ自旋链模型下考虑引入外磁场情况下发现反铁磁性物质要优于铁磁性物质[11].在Heisenberg自旋链模型下的热纠缠容易受到温度、磁场等因素的影响,特别是外加均匀或非均匀的磁场的情况下,从而导致在一定程度上破坏量子信息传输的保真度[12-15].
本文将主要研究不同磁场环境下两量子比特的Heisenberg XXZ自旋链中热量子纠缠特性,采用共生纠缠的方法度量两量子比特的热纠缠,并且比较均匀磁场与非均匀磁场对量子纠缠的影响.
1 理论模型
不同磁场作用的两比特Heisenberg XYZ模型的哈密顿量可以写成如下形式
(1)
在标准基矢{|00〉,|01〉,|10〉,|11〉}下,哈密顿量可以表示为
(2)
相应得出本征值和本征矢分别为
|φ0〉=N1(a|00〉+|11〉)
|φ1〉=N2(b|01〉+|10〉)
|φ2〉=N3(c|01〉+|10〉)
|φ3〉=N4(d|00〉+|11〉)
(3)
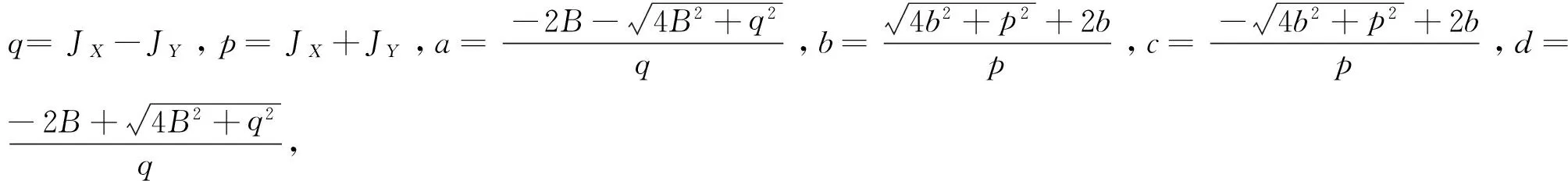
以下定义的共生纠缠度来计算两比特间的此热纠缠.通过密度矩阵ρ=exp(-βH)/Z描述系统的热平衡态,其中β=1/kT,k为玻尔兹曼常数,为方便起见令其为1,Z=tr[exp(-βH)]配分函数.由于ρ描述的是一个热平衡态,因此该纠缠被称为热纠缠.
对于一个密度矩阵ρ表示为Χ类态即:
(4)
根据共生纠缠度方法定义[16-18]为
(5)
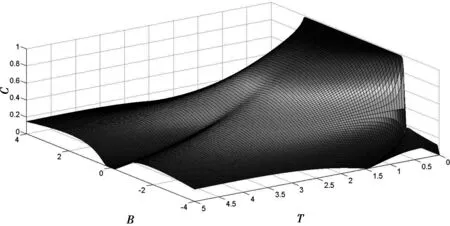
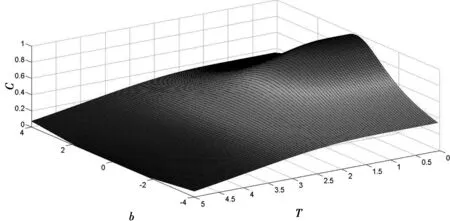
若C(ρ)=0,表示两个子系统是分离;若C(ρ)=1,表示两个子系统处于最大纠缠;若0 该系统的配分函数和密度矩阵如下 (6) 其中 (7) 因此有限温度下的热纠缠为 (8) 当B≠0,b=0时可以看做均匀磁场的情况,当B=0,b≠0时可以看做非均匀磁场的情况,当B=0,b=0时可以看无任何外加磁场的情况,如图1和图2所示,在考虑反铁情况下JX=JZ=1,JY=2的热纠缠与不同磁场的变化图.当无任何外加磁场的时候,给出了固定耦合参数JX,JZ,JY下,系统的共生纠缠度都随着温度的升高而降低最后变为零.但当考虑到外部磁场的影响时,与无任何外加磁场的情况下相比较,发现不同的温度对热纠缠有显著的变化,即量子纠缠随着温度的升高而呈现出缓慢减小的趋势,特别是匀强磁场比非匀强磁场更有用.这是因为温度越高,热起伏越大,系统非纠缠态随着温度的升高而变大,最后导致系统的纠缠度降低,并且当温度达到一个特定值时,一个合适的外加磁场能部分地削弱热波动和提高量子纠缠的作用. 图1 量子纠缠C与温度T的关系,其中:B≠0,b=0. Fig1 The relationship between quantum entanglement C and temperature T,with B≠0,b=0 图2 量子纠缠C与温度T的关系,其中:B=0,b≠0. Fig2 The relationship between quantum entanglement C and temperature T,with B=0,b≠0 本文研究了在3种不同的磁场环境下两量子比特Heisenberg XXZ自旋链中的热量子纠缠特性,并讨论了不同温度和分别作用在每个量子比特上的任意磁场对量子纠缠的影响.文中我们详细推导了共生纠缠度的解析表达式和讨论了不同磁场环境参数中它们的变化趋势.研究结果表明:在有限温度下,不同的磁场导致热量子纠缠的行为显著不同;在某些特定区域内,在有外加磁场的情况下,量子纠缠随着温度的升高而呈现出缓慢减小的趋势.另外,通过调节系统参数在低温度下也可以得到较高的量子纠缠.因此,在量子信息处理过程中,我们可以通过调节外部磁场和温度来实现控制量子纠缠量. 参考文献: [1]BENNETT C H.Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels[J].Phys Rev Lett,1993,70:1895-1899. [2]BENNETT C H.Communication via One- and Two-Particle Operators on Einstein-Podolsky-Rosen States[J].Phys Rev Lett,1992,69:2881-2884. [3]BARENCO A.Dense coding based on quantum entanglement[J].Modern Optics,1995,42:1253-1259. [4]EKERT A K.Quantum Cryptography Based on Bell,s Theorem[J].Phys Rev Lett,1991,67:661-663. [5]HUI X Q,CHEN W X.The entanglement between the boundary qubits in the five-qubit Heisenberg XX open chain[J].Acta Phys.Sin,2006,55:3026-3031. [6]FENG L J,XIA Y J.Entanglement evolution of three twolevel atoms within a common environment[J].Acta Phys.Sin,2015,64:010302. [7]WAQNG X G.Thermal and ground-state entanglement in Heisenberg XX qubit rings[J].Phys Rev A,2002,66:034302. [8]WU N,NANDURI A.Rabi oscillations,decoherence,and disentanglement in a qubit-spin-bath system[J].Phys Rev A,2014,89:062105. [9]MIRZA I M.Two-photo entanglement in multiqubit bidirectional-waveguide QED[J].Phys Rev A,2016,94:012309. [10]QIU L,WANG A M,SU X Q.Effect of Dzyaloshinskii-Moriya anisotropic antisymmetric interaction on optimal dense coding[J].Physica Scripta,2009,79:015005. [11]ZOU Q,HU X M,LIU J M.Effects of Dzyaloshinskill-Moriya interaction and intrinsic decoherence on quantum dense coding via a two-qubit Heisenberg spin system[J].Acta Phys.Sin,2015,64:080302. [12]丛美艳,杨晶黄,燕霞.Dzyaloshinskii-Moriya相互作用和內禀退相干对三粒子XXZ海森堡系统的量子纠缠的影响[J].原子与分子物理学报,2016(2):318-324. [13]杨希,冉扬强.非均匀磁场作用下的混合海森堡XXZ自旋模型的时间演化[J].量子光学学报,2015(4):298-306. [14]谢美秋,郭斌.非均匀磁场中Heisenberg XXZ自旋链的热量子失协[J].武汉理工大学学报,2012(6):1310-1313. [15]刘思平.海森伯格XXZ模型在不均匀磁场下的负值度[J].邵阳学院学报,2011(3):33-36. [16]YU T,EBERLY J H.Finite-Time Disentanglement via spontaneous Emission[J].Phys Rev Lett,2004,93:140404. [17]WOOTTERS W K.Entanglement of formation of arbitrary state of two qubits[J].Phys Rev Lett,1998,80:2245-2248. [18]HORODECKI R,HORODECKI P,HORODECKI M.Quantum entanglement[J].Rev.Mod.Phys,2009,81:865.2 结果与分析
3 结 论
