基于浮动车数据的信号交叉口延误研究
2018-05-16朱海川徐玉静
朱海川,徐玉静
(山东科技大学 测绘科学与工程学院,山东 青岛 266590)
0 引 言
当人们在行驶过程中,多不会选择信号灯多的路口通行,因为在信号灯控制下的路口所花费的时间基本上占整个行驶时间的30%以上[1],因此许多专家和学者把信号交叉口延误作为通行效率高低和信号灯服务水平高低的重要评价指标,在某种程度上反映了资源消耗情况,也反映了信号控制设计是否合理,为城市规划建设提供重要依据[2,3],因此对信号交叉口延误的计算研究具有重要意义.
自Webster提出信号交叉口延误以来[4],相关研究人员一直寻求更好的信号交叉口延误计算方法或模型,主要归纳为点样本调查法、参数公式法、模拟仿真法[5].对于点样本调查法,Limanond等[6]通过对两个物理条件相同的信号交叉口(信号灯是否有倒计时为不同条件)进行连续24 h监控,结果表明有倒计时的信号交叉口的延误平均减少1.00~1.92 s;孙剑,等[7]提出以每个信号周期为计算单元的基于两个检测截面交通参数的“总体抽样”车辆引道延误方法.点样本法是通过真实情况的实测,不受样本错误或遗漏的影响,能够比较真实地反应信号交叉口的延误情况,但是获取大样本数据要耗费较多人力和财力,不适用于大样本的信号交叉口延误的获取.对于参数公式法,HCM2010延误模型[8]通过流率、畅行速度、绿信比等参数计算信号交叉口延误,该模型是通过数学公式实现延误;黄崇超等[9]在已知信号交叉口处的车辆排队长度和车流到达率的情况下,利用信号周期、平均排队长度和流率等参数获取信号交叉口延误值.参数公式法是在特定参数假设的基础上完全通过数学公式计算信号交叉口延误,面对更新较快的复杂混合交通情况和众多随机因素的影响,有时难以反映真实情况.信号交叉延误模拟仿真主要有Vissim、Paramics和SimTraffic等,是通过软件模拟车辆经过信号交叉口的全过程,调整交通参数分析不同的模拟方案从而得到接近真实的结果[10].模拟仿真方法能较真实地反映和重现信号交叉口的交通情况[11],但是必须通过设定交通和车辆特性参数才能保证延误精度.
在信号交叉口延误模型的发展过程中,车辆通过信号交叉口的延误分析或延误模型基本上都没有大的变化,多为根据当时实际交通情况的需要对原有的方法或公式进行修正,让使用的相应方法或公式获取的结果更加接近现场实测的数据.随着浮动车技术在智能交通系统中应用越来越广泛,信号交叉口又是智能交通系统监控的主要对象,因此浮动车采集的数据可为信号交叉口延误的计算提供真实可靠的数据源,利用大样本浮动车数据计算信号交叉口延误的研究正广泛的深入[12,13].
浮动车数据具有全天候、高覆盖率、低成本、实时性等优点[14],可以将浮动车数据作为大样本数据应用到信号交叉口延误计算中,但是在计算过程中牵扯到大规模矩阵计算,计算速度慢,执行效率低,因此在保证精度的前提下通过并行化的方式进行加速,以期缩短执行时间提高执行效率.
1 信号交叉口延误模型
根据信号交叉口延误定义,以浮动车作为信号交叉口延误的数据源,信号交叉口的延误的影响范围和浮动车的畅行速度是获取信号交叉口延误值的决定因素.
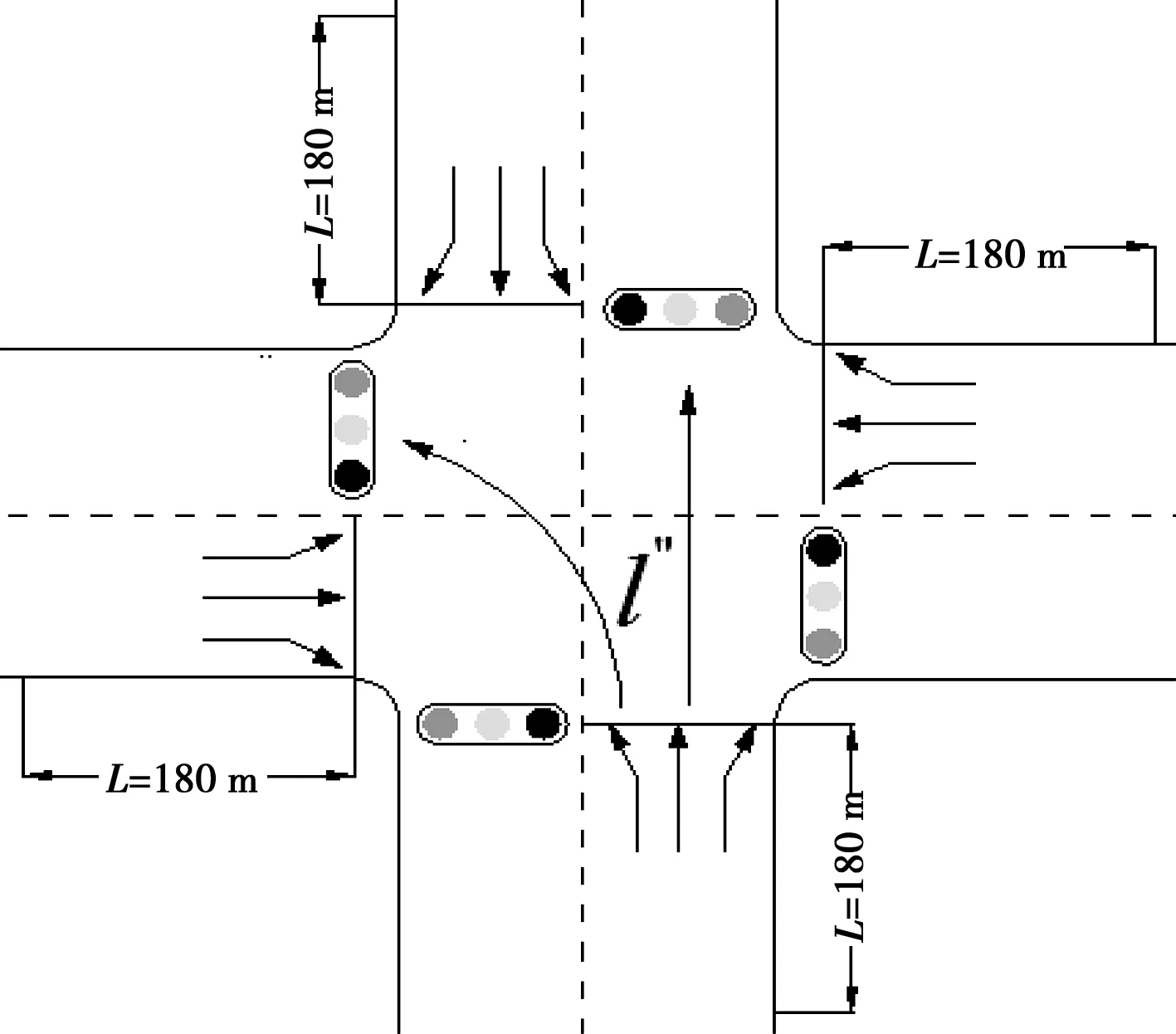
图1 信号交叉口影响范围 Fig.1 The influence of Signalized intersection
1.1 信号交叉口影响范围界定
根据信号交叉口检测器的距离设定和城市道路的相关法律法则以及对信号交叉口影响范围的调查,一般情况下,信号交叉口的影响范围L的设定距离为140~180 m[15,16].
信号交叉口影响范围的界定也要根据实际情况而定,本文以北京市的信号交叉口为研究对象,考虑到信号交叉口处的车辆实际排队长度,结合信号交叉口影响区域范围的标准,本文选取信号交叉口的影响范围L=180 m,以信号交叉口转角缘石曲线端点为始点,并以车辆行驶的方向为转向,设定信号交叉口的影响范围L=180 m,如图1所示.
1.2 信号交叉口的畅行速度界定
计算信号交叉口延误值的另一个关键是获得浮动车经过信号交叉口的畅行速度,虽然浮动车在不同类型道路上的畅行速度不同,根据我国城市交通规定[15],信号交叉口范围内的畅行速度V畅如表1所示,信号交叉口范围内的畅行速度V畅依据我国城市交通规定的速度设定.

表1 城市道路设计车速
1.3 信号交叉口延误计算
当浮动车非右转状态下通过信号交叉口时,浮动车不仅要行驶L的距离,还有通过导流线包围的区域l″,则在整个信号交叉口影响范围内行驶的距离L″等于L+l″.在信号交叉口范围的某个弧段的距离较小,其速度的变化率几乎为零,认为车辆行驶的距离与速度呈线性正比关系,浮动车通过信号交叉口范围的处理过程如图2所示,浮动车在驶入信号交叉口和驶离信号交叉口时遵循公式(1)和公式(2).
(1)
(2)
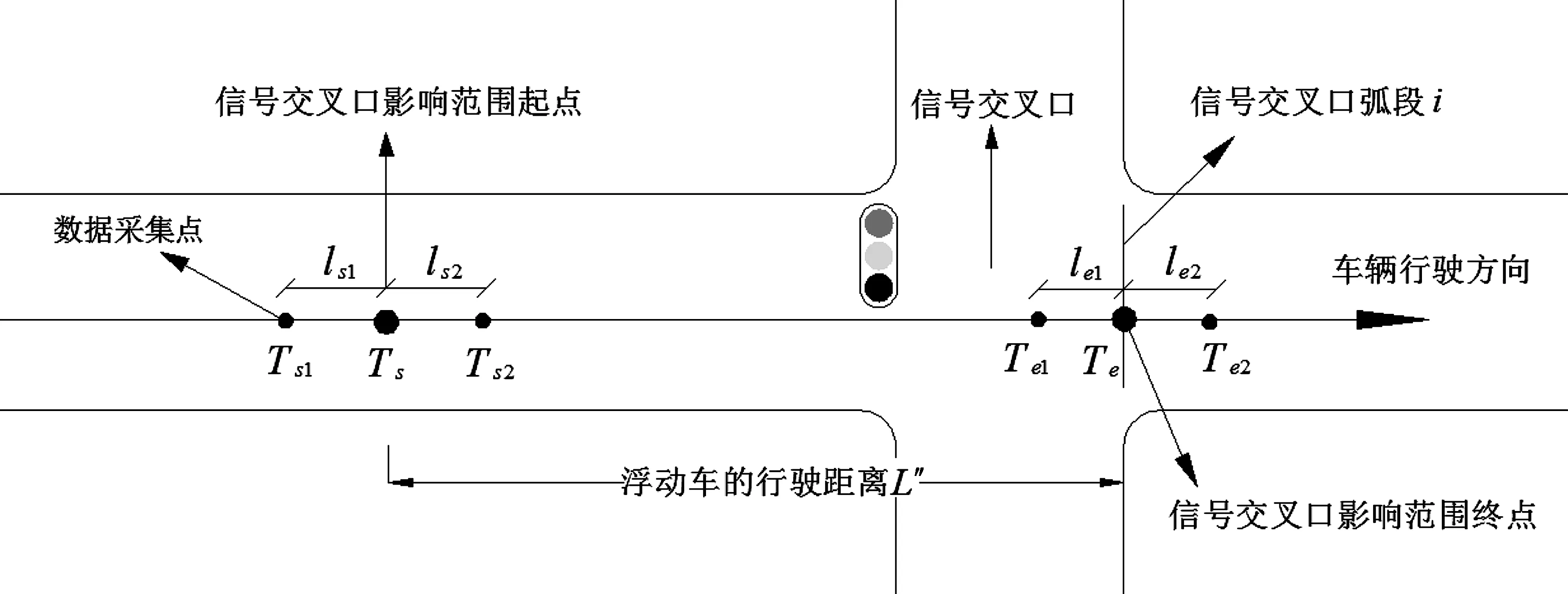
图2 信号交叉口范围的起终点的浮动车数据处理流程 Fig.2 Signalized intersection range of the end point of the floating car data processing flow
由公式(1)、(2)可以推出的结果:
(3)
公式(1)、(2)、(3)中,Ts、Te为浮动车驶进、驶离信号交叉口影响范围的时刻,Ts1、Ts2为浮动车驶进信号交叉口时的临近上下游时刻,ls1为Ts1与Ts时间段内浮动车行驶的距离,ls2为Ts2与Ts时间段内浮动车行驶的距离,Te1、Te2为浮动车驶离信号交叉口时的临近上下游时刻,le1为Te1与Te时间段内浮动车行驶的距离,le2为Te2与Te时间段内浮动车行驶的距离.
由公式(3)知,Ts1、Ts2、Te1、Te2可有浮动车数据获得,ls1、ls2、le1、le2可有浮动车的经纬度坐标获取.以(xs,ys)和(xe,ye)表示为Ts、Te时刻浮动车在信号交叉口弧段处经纬度坐标,(xs2,ys2)为Te2时刻浮动车的坐标,(xe2,ye2)为Te2时刻浮动车的坐标,则浮动车经过信号交叉口时的延误值d计表示为:
d计
(4)
2 数据的筛选与存储
2.1 数据筛选
2012年03月01日的浮动车数据约有1561万条轨迹,浮动车数据随方位角、瞬时速度、时间分布和采集时间间隔变化分布如图3、图4、图5、图6所示.图3中横坐标为浮动车方向角,图4中横坐标为浮动车瞬时速度(m/s),图5中横坐标为时间,图6中横坐标为时间间隔(s),竖坐标均为浮动车数据轨迹数目.从图3中看出,浮动车的行驶方向是相对均匀的,从图4看出,浮动车速度多在10-15 m/s之间,从图5看出,浮动车数据多在7∶00-9∶00和17∶30-19∶30时间段,从图6看出,浮动车的数据采集时间间隔多在10-40 s之间.为了获取更加准确的信号交叉口延误值,要充分考虑数据的真实可靠性,因此,选用分布在8∶00-9∶00时间段内、采集时间间隔为10-40 s之间和浮动车瞬时速度为10-15 m/s的浮动车数据.
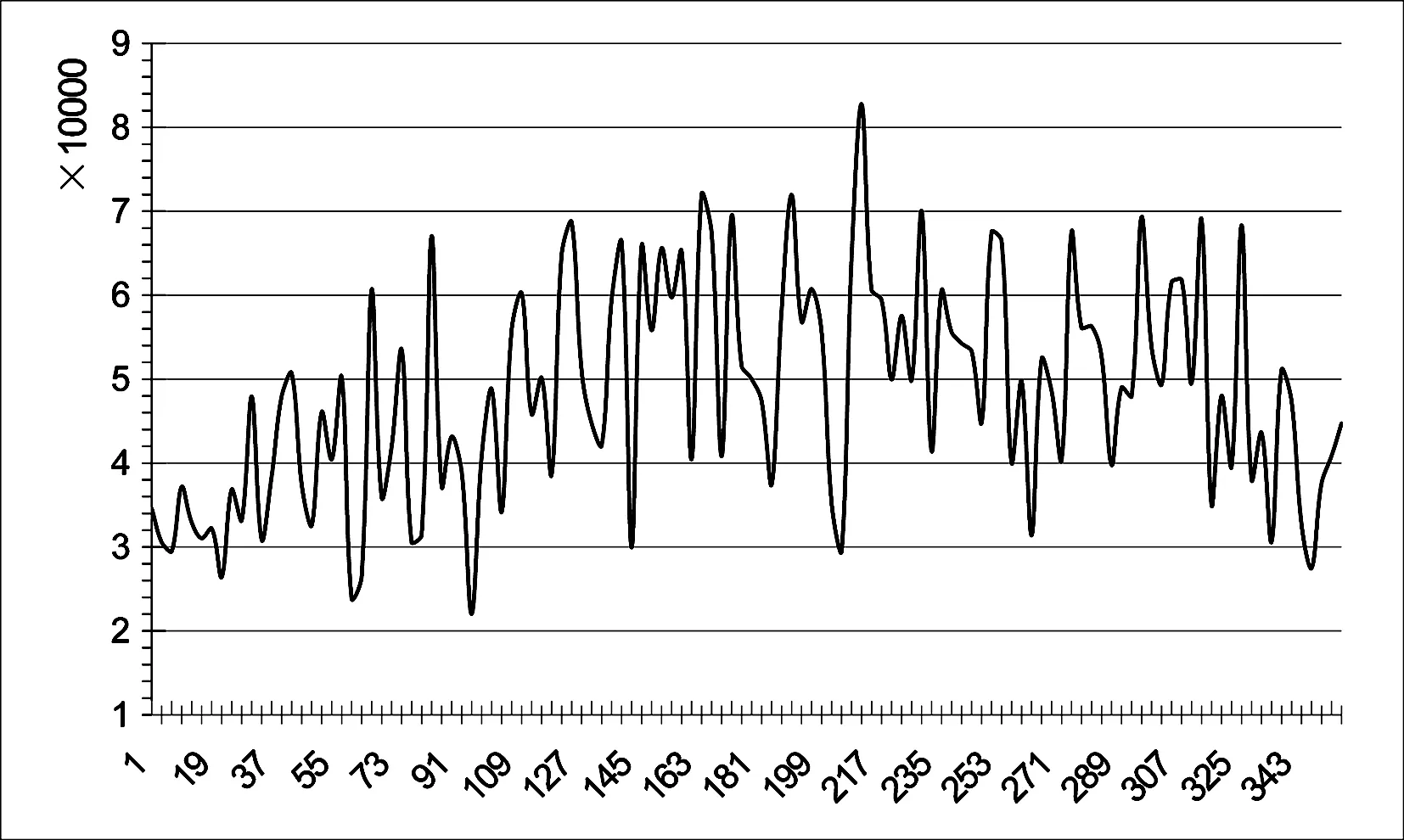
图3 浮动车行驶方向分布图 Fig.3 The direction of floating car
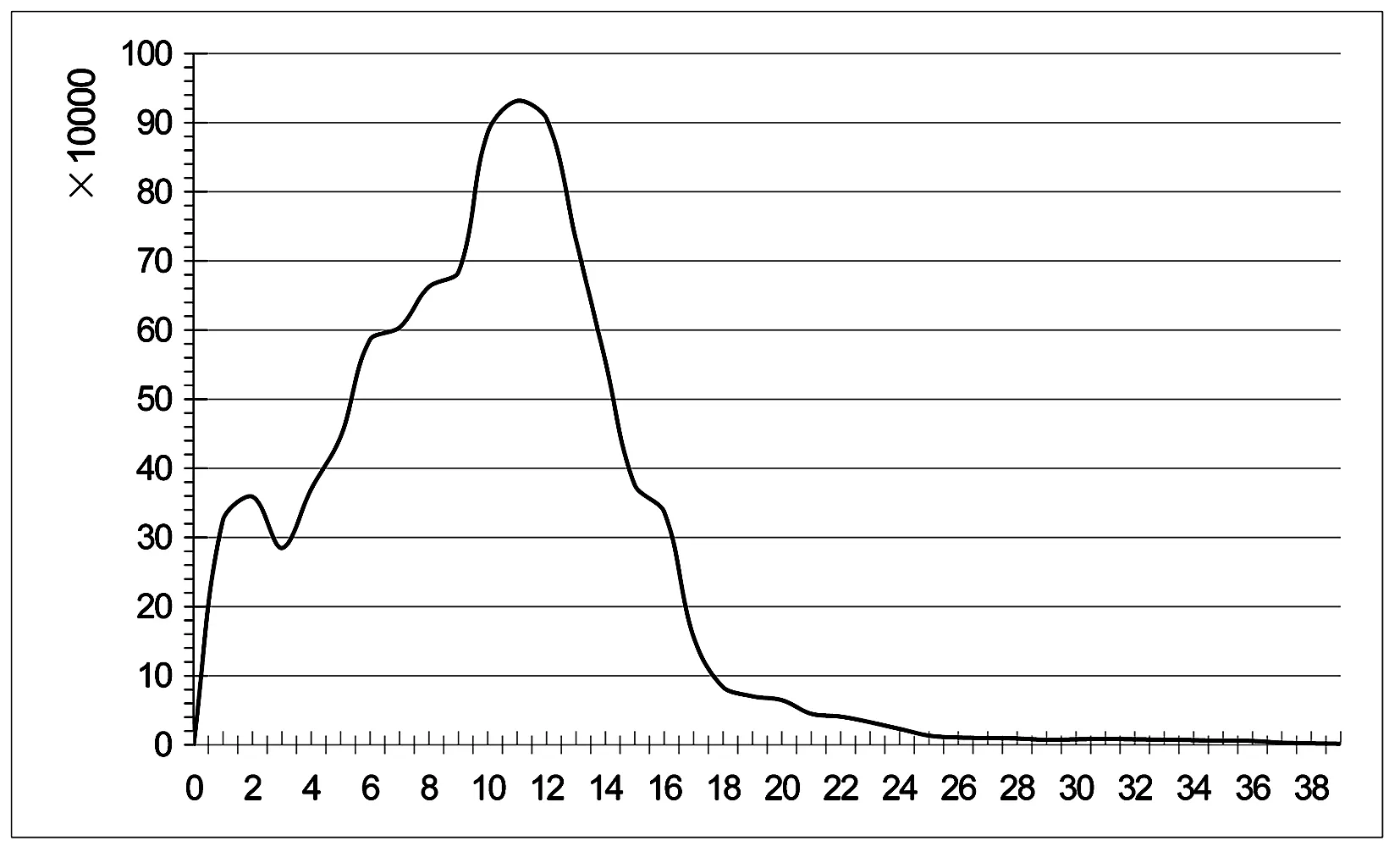
图4 浮动车速度分布图 Fig.4 The speed of floating car

图5 浮动车数据的时间分布 Fig.5 The change of data volume of floating car with time
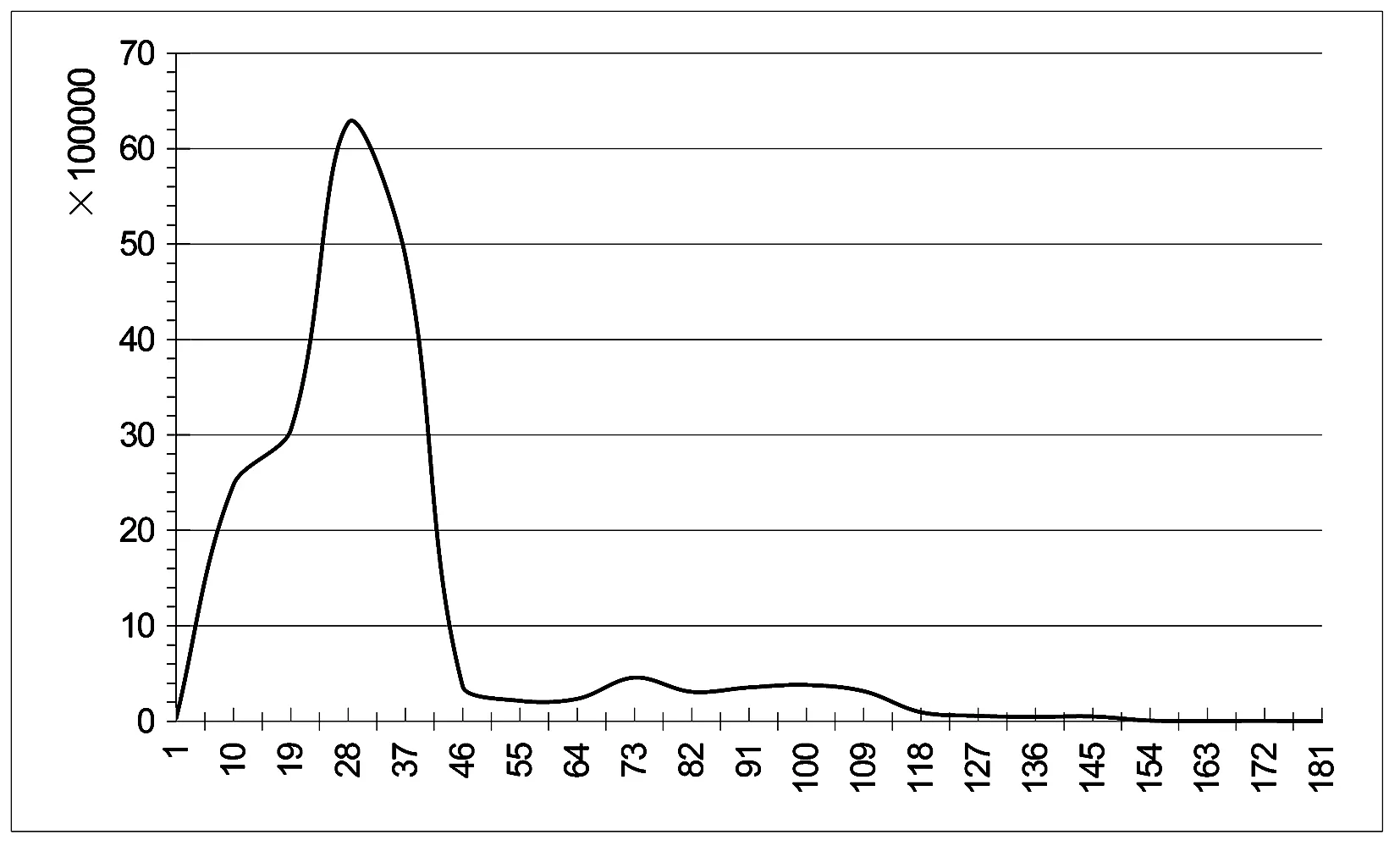
图6 浮动车数据采样时间间隔分布 Fig.6 Distribution of data sampling interval of floating car
2.2 数据的存储
Hama作为Hadoop项目的服务于大规模的矩阵、图论和网络计算的子项目,它是建立在Hadoop平台之上的,利用Hadoop平台的分布式存储系统HDFS(Hadoop Distributed File System,Hadoop分布式文件系统)[12],提供基于BSP(Bulk Synchronous Parallel,整体同步并行)模型和graph模型的计算框架.
利用大样本浮动车数据计算信号交叉口延误的运行效率关键在于信号交叉口数据与浮动车数据矩阵的运算效率[17].在早期Hama框架中,矩阵数据主要存储在建立在HDFS之上的HBase数据库中,HBase中数据是面向列进行存储的,HBase是以列的方式进行存储,对其row-key的设计较为复杂.现如今,数据以二进制序列化的
3 实验分析
3.1 精度分析
理论上Vissim模拟仿真可以获取任意时间的信号交叉口延误值,而且结果更加接近实地调查值[20],由于受到数据和时间的限制,本文并未获得实地交叉口延误调查值,而是选用Vissim模拟仿真获取的延误值作为信号交叉口延误实际值.随机抽取20个以本文方法获取的信号交叉口延误的计算结果与Vissim模拟仿真获取的信号交叉口延误实际值对比,具体结果如表2所示,表2中T实、d实为浮动车通过信号交叉口的实际运行时间和实际延误值.

表2 信号交叉口计算结果
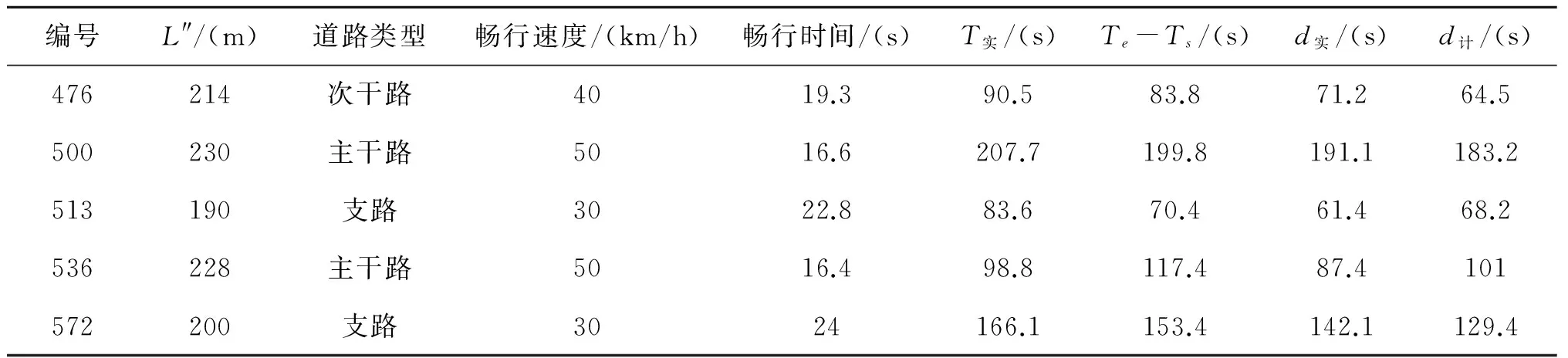
续表2
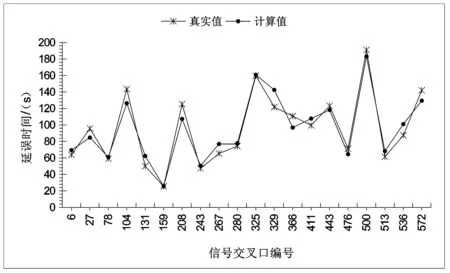
图7 信号交叉口延误实际值与计算值对比 Fig.7 Comparison of actual value and calculated value of signalized intersection delay
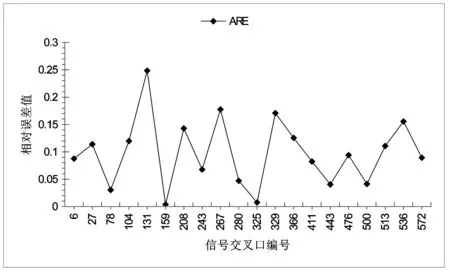
图8 信号交叉口延误相对误差 Fig.8 The ARE distribution of signal intersection delay
由图7、图8可知,以浮动车数据为数据源的基于Hama并行分布式平台的信号交叉口延误的计算值与信号交叉口延误实际值十分接近,有些信号交叉口延误的计算值与实际值基本吻合,计算值的相对误差在15.6%以内,计算值的精度大于84.4%,使用浮动车数据获取的信号交叉口延误值精度较高,浮动车数据的信号交叉口延误能真实反映延误情况.
3.2 效率分析
实验运行环境:使用VMware Workstation 11设置7个虚拟机部署Hama环境,其中1个作为管理节点,6个作为计算节点;以16G内存、Intel(R)Core(TM)i5-2410M CPU @2.30GHZ的处理器作为宿主机;JDK-7u79的java环境;apache-hadoop-2.6.0版本的hadoop环境;apache-hama-0.7.0版本的hama环境.
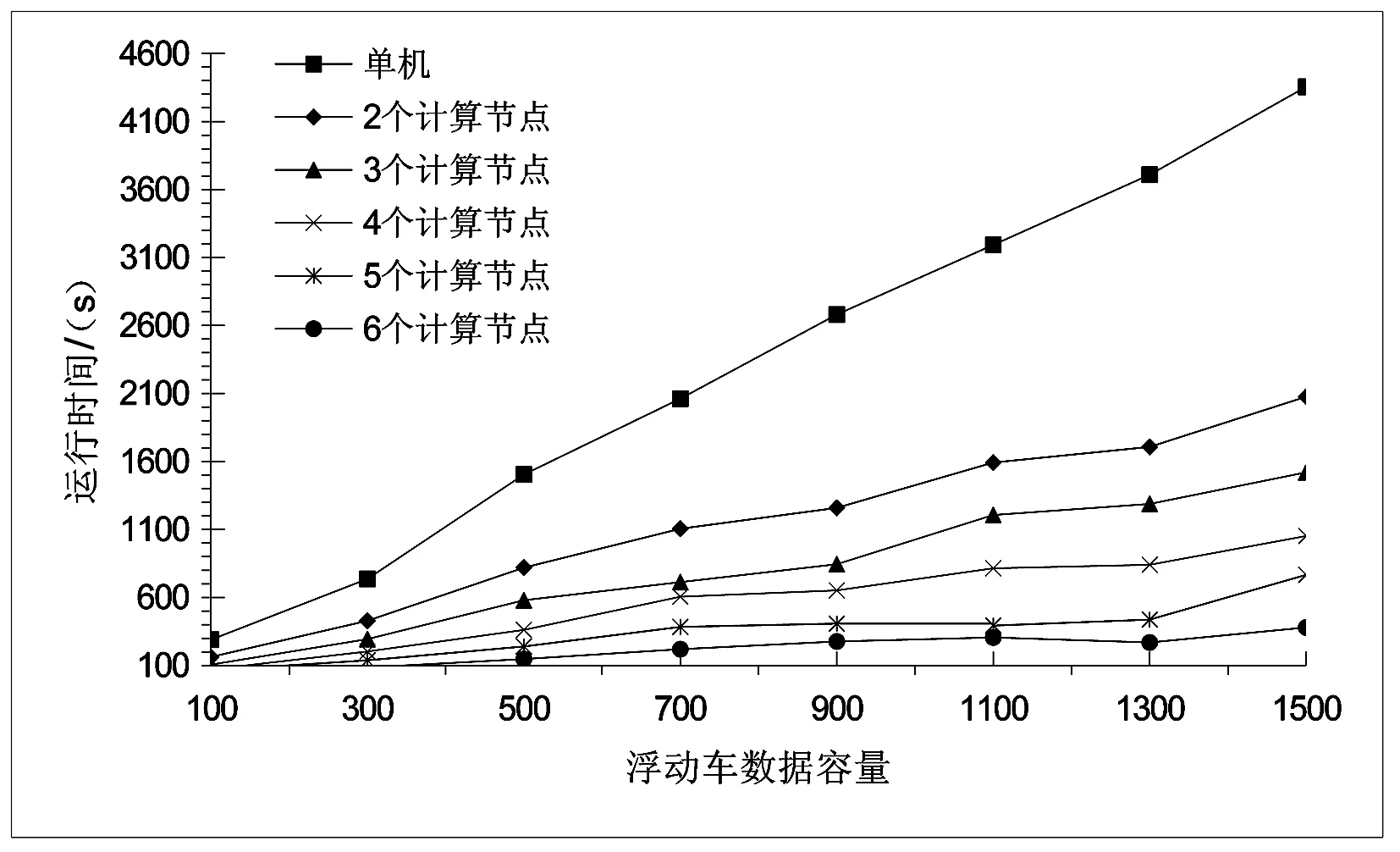
图9 实验运行时间对比 Fig.9 comparison of running time
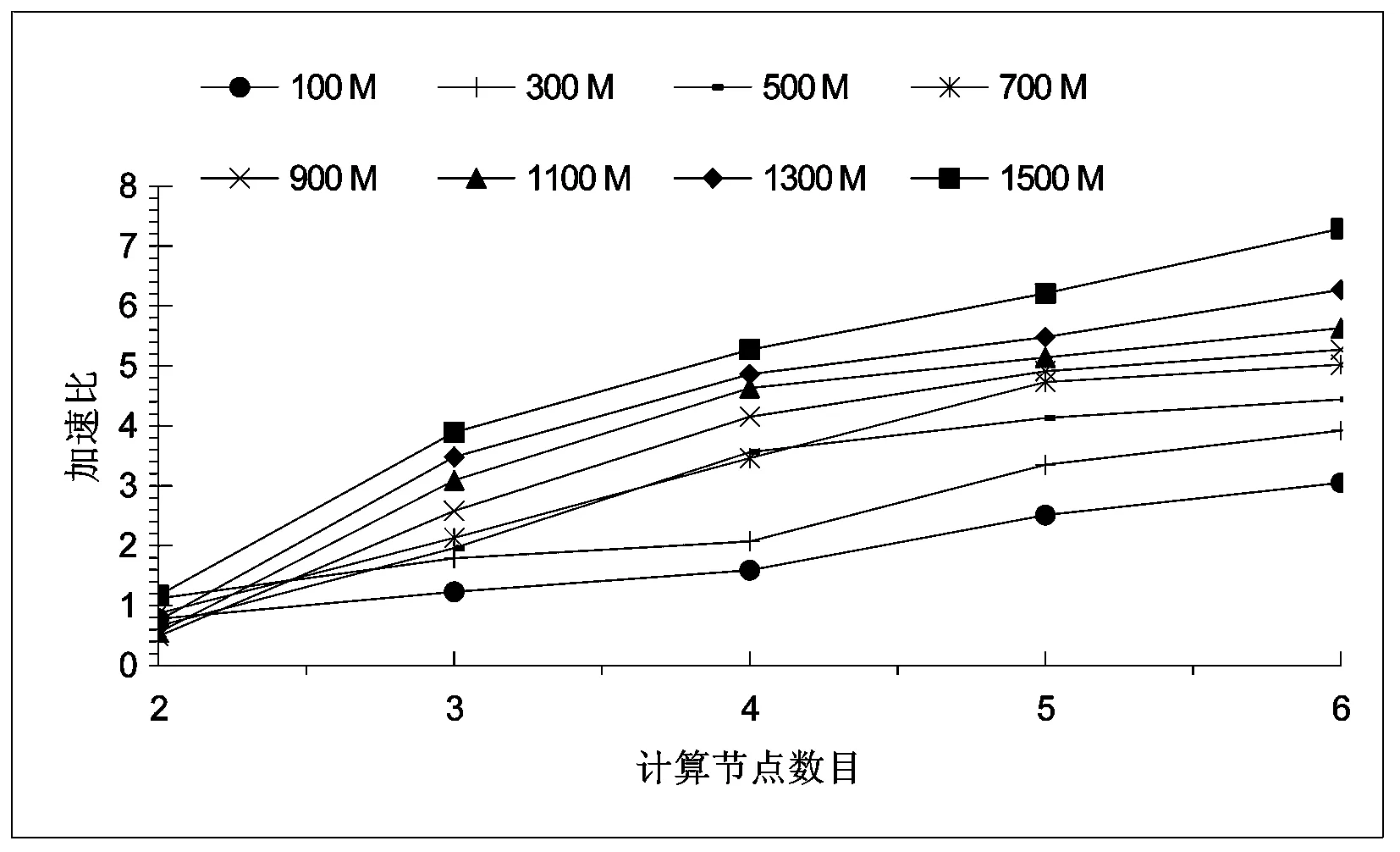
图10 集群加速比 Fig.10 cluster speedup
以Hama集群实现大样本浮动车数据的信号交叉口延误计算,Hama集群中配置6个计算节点,数据容量分别为100 M、300 M、500 M、700 M、900 M、1100 M、1300 M、1500 M,运行结果如图9、图10所示.从图10可知,当浮动车数据量较小时,计算节点的加速比并不理想,集群的加速比是随着数据量的增加或计算节点的增多而增大,以6个计算节点为例,数据容量为1500 M时,集群的加速比是单机版的9.3倍,在一定Hama集群规模下,Hama集群实现大样本浮动车数据的信号交叉口延误计算具有良好的性能.在理想情况下,Hama集群的加速比与计算节点的数目呈现正比线性关系,但是在实际应用过程中,由于数据加载、数据分隔、网络通信、数据信息传输等因素影响Hama性能[22].
4 结 论
本文在分析浮动车数据的信号交叉口延误方法的基础上,通过界定信号交叉口影响范围和车辆经过信号交叉口的畅行速度等参数,在并行分布式Hama集群上对其进行并行化实现来提高处理效率,结合北京市主要信号交叉口的延误值,以Vissim获取的信号交叉口延误的真实值与以浮动车数据进行计算而得到的计算值作对比,并分析信号交叉口延误的精度和获取的效率情况.Hama并行分布式实现的大样本浮动车数据的信号交叉口延误计算,计算结果的精度在84.4%以上,以6个计算节点为例,集群执行效率是单机版的9.3倍,延误值不仅具有良好的精度,而且对其的计算效率具有显著提高,对实际应用具有一定的意义.
参考文献:
[1]刘岩.考虑车辆运动行为的信号交叉口延误研究[D].吉林大学,2016:1-7.
[2]刘好德.城市道路交通状态信息服务系统设计与实现[J].测绘科学,2012,37(6):169-171.
[3]赖元文,S EASA.信号交叉口通行能力随机影响因素建模[J].中国公路学报,2016,29(11):130-138.
[4]Webster F V.Traffic signal settings[R].Road Research Technical Paper No.39,Road Research Laboratory,London,1958.
[5]陈绍宽,郭谨一,王璇,等.信号交叉口延误计算方法的比较[J].北京交通大学学报,2005,29(3):77-80.
[6]Limanond T,Chookerd S,Roubtonglang N.Effects of countdown timers on queue discharge characteristics of through movement at a signalized intersection[J].Transportation Research Part C Emerging Technologies,2009,17(6):662-671.
[7]孙剑,潘斌,李克平,等.非饱和信号控制交叉口动态延误测定方法[J].同济大学学报(自然科学版),2011(7):1007-1012.
[8]Transportation Research Board.Highway Capacity Manual[M].Washington DC:National Research Council,2010.
[9]黄崇超,于刚.交叉口延误函数与实时信号配时优化模型[J].武汉大学学报(工学版),2006,39(5):71-76.
[10]Essa M,Sayed T.A comparison between PARAMICS and VISSIM in estimating automated field‐measured traffic conflicts at signalized intersections[J].Journal of Advanced Transportation,2016,50(5):897-917.
[11]周志浩,葛欢.基于VISSIM仿真的信号交叉口优化方法研究[J].交通标准化,2013(2):134-137.
[12]王凯,曹建成,王乃生,等.Hadoop支持下的地理信息大数据处理技术初探[J].测绘通报,2015(10):114-117.
[13]张希瑞,方志祥,李清泉,等.基于浮动车数据的城市道路通行能力时空特征分析[J].地球信息科学学报,2015,17(3):336-343.
[14]余洋.云计算环境下的大样本浮动车数据处理关键技术研究[D].武汉大学,2010:16-24.
[15]中华人民共和国建设部.GB 50220-95.城市道路交通规划设计规范[S].中国计划出版社,1995.
[16]Siddique K,Akhtar Z,Yoon E,et al.Apache Hama:An Emerging Bulk Synchronous Parallel Computing Framework for Big Data Applications[J].IEEE Access,2016,PP(99):1.
[17]李清泉,李德仁.大数据GIS[J].武汉大学学报(信息科学版),2014,39(6):641-644.
[18]苏韦,李景文,刘华尧,等.基于MapReduce的时空数据模型设计方法[J].测绘与空间地理信息,2013,36(7):41-44.
[19]Essa M,Sayed T.A comparison between PARAMICS and VISSIM in estimating automated field‐measured traffic conflicts at signalized intersections[J].Journal of Advanced Transportation,2016,50(5):897-917.
[20]Lai S,Lai G,Lu F,et al.A BSP model graph processing system on many cores[J].Cluster Computing,2017:1-19.
