基于bootstrap小样本数据的判别分析

刘媚，白岩

(宁夏师范学院 数学与计算机科学学院，宁夏 固原 756000)

1 问题的提出

企业信用风险评估，一直是金融经济学理论领域关注和探讨的问题，尤其随着近年来国家对小微企业的扶持力度增加，金融机构对中小企业的融资政策也会放宽.但是由于小企业本身数据较少，质量不高，精度不够，这些都影响银行和投资人的评判，也增加了投资的风险.1968年美国纽约大学商学院Altman教授提出了应用于商业的Zeta模型[1]，后来，Edmister教授提出了针对小企业的财务风险判别分析模型[2].如何对小企业的信用风险，进行恰当的评估成为降低小企业信用风险的有效方法，文章结合实际企业的财政数据，利用不同的抽样方法，针对小样本数据进行判别分析，比较这些研究方法在金融领域应用的有效性和实用性.

2 判别分析

判别分析是利用已知类别的样本培训模型，为未知样本判类的一种统计方法.它产生于19世纪30年代.它的特点是根据已掌握的、历史上每个类别的若干样本的数据信息，总结出客观事物分类的规律性，建立判别公式和判别准则.然后，当遇到新的样本点时，只要根据总结出来的判别公式和判别准则，就能判别该样本点所属的类别.

判别分析就是将P维Euclid空间Rp划分成k个互不相交的区域R1,R2,……Rk，且Ri∩Rj=φ,i≠j,i,j=1,2…k.当x∈Ri,i=1,2…,k,就判定x属于Xi,i=1,2,…,k.

判别分析应满足的基本条件：

(1)预测变量尽可能服从正态分布；

(2)所选择的预测变量之间的相关性较弱且保持一致；

(3)预测变量应该是连续、不间断变量，而判别类别或组别是间断变量；

(4)预测变量的平均值和方差没有相关性.

应用Feshir方法进行实际分析时要注意：样本空间的数量尽可能大；对已知因变量的分类或分组要尽可能客观、准确、可靠.这样建立的判别函数才能起到准确的判别效果.

2.1 Feshir判别

Fisher判别的基本思路就是投影，针对P维空间中的某点x=(x1，x2，x3...，xp)寻找一个能使它降为一维数值的线性函数

y(x)：y(x)=∑cjxj

然后应用这个线性函数，把P维空间中的已知类别总体，以及求知类别归属的样本都变换为一维数据，再根据其间的亲疏程度，把未知归属的样本点判定其归属.这个线性函数应该满足，能够在把P维空间中的所有点转化为一维数值之后，既能最大限度地缩小同类中各个样本点之间的差异，又能最大限度地扩大不同类别中各个样本点之间的差异，这样才可能获得较高的判别效率.在一般利用一元方差分析的思想，即依据组间均方差与组内均方差之比最大的原则，来进行判别.

2.2 判别结果检验

由于概率分布的选取会造成计算结果的差异，影响判断和决策的制定，而小样本数据恰好会影响总体的估计，所以可以通过抽样方法改善小样本数据的先天不足.常用最简单的抽样方法是直接抽样、重复抽样，另外还有bootsrap方法，该方法可以将小样本问题转化为大样本问题来估计未知参数的近似分布，下面就利用不同的抽样方法对实际观测数据进行判别分析.

3 基于bootstrap的判别分析

以宁夏银川市某商业银行为例，截止到2013年9月末，信贷资产总额207亿元，5级分类口径不良贷款余额为3.87亿元，不良贷款率1.47%.全行公司类信贷客户89户，分布在37个行业，列前3位的是采矿业，贷款余额39亿元；制造业，贷款余额32亿元；批发业，贷款余额29亿元；以上3个行业贷款占全行贷款余额的60%.对该行信贷数据进行随机抽样得到44个观测值利用不同的抽样方法进行分析.

3.1 bootstrap方法

bootstrap(自助法或自助抽样法)方法，是根据给定的原始样本，复制观测信息对总体的分布特性进行统计推断，不需要额外的信息.Efron(1979)认为该方法也属于非参数统计方法.bootstrap方法从观察数据出发，不需任何分布假定，是频率论中一种决定误差的方法(Efron，1979；Hastie et al.，2001).这种方法中，使用下面的方式创造多个数据集：假设我们的原始数据集包含N个数据点X=x1,x2,…xN.我们可以通过随机的从X中取N个数据来创建数据集XB，选取是可以重复的，所以有些X中的点可能在XB中出现多次，而有些可能不出现.这样的过程可以重复L次，得到L个大小为N的通过对原数据集X采样得到的数据集.参数估计的统计精确度就可以通过考察不同的自助数据集之间的预测变异性来进行评估.因而，bootstrap方法能够解决许多传统统计分析方法不能解决的问题.是一种从给定训练集中有放回的均匀抽样，即每当选中一个样本，它等可能地被再次选中并被再次添加到训练集中.其核心思想和基本步骤如下：

(1)采用重抽样技术从原始样本中抽取一定数量(自己给定)的样本，此过程允许重复抽样.

(2)根据抽出的样本计算给定的统计量T.

(3)重复上述N次(一般大于1000)，得到N个统计量T.

(4)计算上述N个统计量T的样本方差，得到统计量的方差.

应该说bootstrap是现代统计学较为流行的一种统计方法，在小样本时效果很好.

利用bootstrap方法对44个观测值抽样后重新进行判别，样本为1000，分类函数为：

判别分析结果见表1：

表1 bootstrap分类结果

3.2 重复抽样的方法对数据进行判别分析

用现有的数据分别取概率(0.7，0.3)产生训练集和预测集得到的判别结果见表2.

表2 重复抽样分类结果

3.3 根据实数据直接进行判别分析

利用现有17个数据作为训练集，27个测试集进行判别，结果如表3.

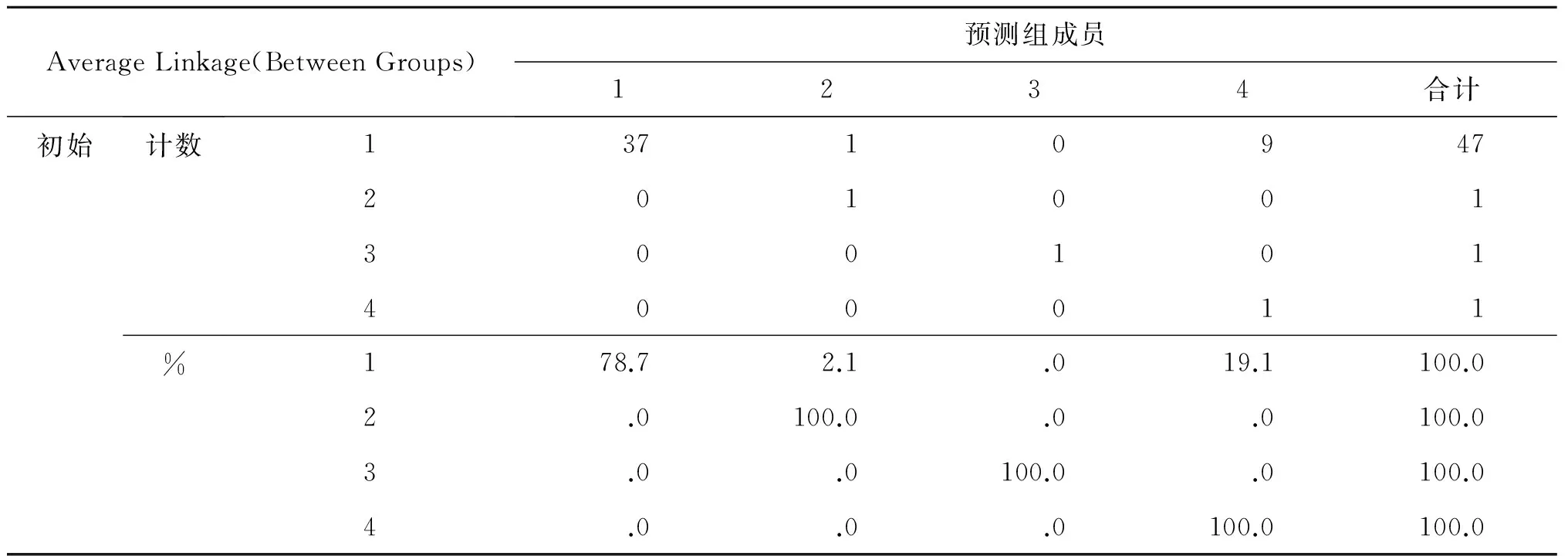
表3 直接法分类结果

利用三种不同方法进行判别分析后，得到的判别结果和判错率由表1、2、3给出，对于3种判别方法的检验见表4，可以看出这3种方法的判别函数均有效.由于bootstrap方法判错率最低.所以对于少数民族地区小企业这样的小样本数据，进行信用风险估计时，可以利用该方法进行判别分析.

表4 3种不同方法判别分析函数检验的Wilks的Lambda

参考文献：

[1]ALTMAN E I.Financial ratios，discriminant analysis and the prediction of corporate bankruptcy[J].Journal of Finance,1968,10：5892609.

[2]EDM ISTER R.An empirical test of financial ratio analysis for small business failure prediction[J].Journal of Finance Quantitative Analysis，1972，5：147721493.

[3]Efron.Bootstrap Methods：Another Look at the Jackknife[M].The Annals of Statistics,1979，7：1-26.