基于随机森林回归的草场植被盖度反演模型研究——以新疆阿勒泰地区布尔津县为例

陈 妍, 宋豫秦,*,王 伟

1 北京大学环境科学与工程学院, 北京 100871 2 中国环境科学研究院生物多样性研究中心,北京 100012

我国是草地资源大国,但多年来的超载过牧、荒地过度开垦和滥挖乱采致使草场植被覆盖度大幅下降,水土流失和沙漠化日趋严重,牧区经济发展及草地生态系统的健康因此受到了严重威胁[1]。研究草场变化规律是揭示草场退化驱动力以及风险评估的基础,在缺乏长期监测数据的情况下,借助卫星遥感影像不失为有效的方法。当前可用的遥感数据一般为气象卫星NOAA的1km分辨率AVHRR数据[2- 3],terra和aqua卫星的250m分辨率MODIS数据[4- 5]和陆地卫星Landsat系列数据。早期研究多采用分辨率较低的AVHRR数据,MODIS数据虽具有较高的完整性,但仍难以满足长时间序列研究的需求。Landsat系列卫星自1975年开始已有7颗卫星相继运行,且其30m的分辨率相较于AVHRR和MODIS来说优势明显,因而被目前不少研究者所关注。

利用遥感影像研究草场变化趋势大致可分为两种思路,其一是通过监督或非监督分类,分析草场分布或面积的变化[6- 8],然而面积增减只能体现宏观变化,难以反映某一具体区域在时间序列上的退化或恢复情况;其二是利用光谱信息计算植被指数,通过植被指数变化直接表征生态系统的变化趋势[9- 11],相对而言,这类方法的主要优势是将研究对象精确至像元尺度。然而干旱半干旱地区植被盖度低,植被光谱信息弱,植被指数往往非常小,在这种情况下用其变化情况说明草场生态的改善或恶化往往意义不大。而利用植被指数反演植被盖度不失为一种可行的替代思路。植被盖度计算主要可通过线性光谱混合模型[12- 14]和回归模型两种方法实现。前者一般应用于缺乏地面监测数据的情况之下,其核心是获得纯像元下的地物光谱值。但在实际应用中,特别是植被盖度较低的草地生态系统中,典型光谱值很难获得,且计算误差较大[15]。因此,在具备地面监测数据的情况下,一般通过植被指数与植被盖度直接的相关关系建立参数模型,反演植被盖度,其中线性回归模型应用最为广泛[16- 17]。然而以往的研究多未充分考虑参数回归苛刻的假设条件,以及多元回归对变量间非共线性的要求,这无疑会降低反演模型的可靠性。解决此问题的途径之一是寻求预测效果达到甚至超越参数模型的非参数方法。作为目前预测效果最好的非参数回归模型之一,随机森林模型与参数回归等方法相比,无需对变量的正态性和独立性等假设条件进行检验,同时也不需要考虑多变量的共线问题[18],且运算高效、结果准确,在环境以及生态学等领域都有着广泛应用[19- 22]。在草场研究方面,随机森林虽曾用于植被分类[23],但作为回归模型的应用则几属空白。

数据源是保证反演模型可靠性的前提,长时间序列研究会不可避免地使用到来自不同传感器的光谱信息,而对于Landsat系列卫星标准数据产品而言,同一时间段内从不同传感器所提取的光谱信息会存在一定差异,需要对非同源数据进行校正以及标准化处理[24- 25]。但目前草场方面已有的研究既没有定量分析传感器差异对反演结果造成的影响,也没有计算校正和标准化处理对反演结果的改进效果。

鉴此,本文利用Landsat系列卫星TM,ETM+以及OLI的影像和植被盖度地面监测数据建立基于随机森林回归的草场植被盖度反演模型,并将反演结果与线性回归结果进行比对,探讨其优越性。继之将其应用于基于多源数据的草场植被盖度变化趋势分析,并探讨该方法的不确定性,以期为干旱半干旱地区长时间序列的草场变化研究提供方法支持。

1 研究区域

布尔津县位于新疆西北部阿勒泰地区,属阿尔泰山脉西南麓,介于86°25′—88°6′E,47°22′—49°11′N之间,总面积10369km2。境内景观异质性强,北部山区最高蜂海拔4374m,中部为低山丘陵、河谷地带,南部为低平戈壁滩，海拔最低处仅为436m(图1)。全县生态系统多样,北部山区兼具水源涵养与生物多样性保护的功能,南部荒漠生态系统肩负防风固沙的生态功能。草地资源丰富,各类草地类型均有分布,农业以畜牧为主,放牧方式仍属传统游牧。当前北部林区载畜量快速增加,林牧矛盾突出,南部以荒漠植被为主,生态环境脆弱,生态保护形势更加严峻。丰富而多样的草场分布特征,不仅可使草场植被盖度反演模型为分析当地草场历史变化趋势乃至制定草场保护和畜牧业生产政策奠定基础,同时也可为其他地区的各类草场研究提供一定借鉴。

2 数据获取与预处理

为了建立基于随机森林回归的草场植被盖度反演模型,本文所用之数据主要包括基于地面调查的草场盖度数据和卫星遥感影像。

植被盖度地面调查数据来源于布尔津县畜牧兽医局草原站提供的2010、2011、2013、2014、2015年6—9月的草本、半灌木及矮小灌木草原样方调查表。调查样地涵盖全县8个典型草场类型,即低平地草甸、高寒草甸、山地草甸、温性草甸草原、温性草原化荒漠、温性荒漠以及温性荒漠草原。依据典型性原则,样方在能够代表整个样地草原植被、地形及土壤等特征的区域随机布设,监测样地共计205个,分布及类型如图1所示,每个样地设置3个样方,样方大小为1m×1m,监测结果用3个样方的平均值表示。部分监测点位虽然超越了县界,但并未超越本文所用的遥感影像范围,因此本文将此类监测点也纳入分析范围。植被盖度是由目测法测定的样方内植物地上部分垂直投影面积占样方面积的比率,监测频次为每年一次。

遥感数据为下载自美国地质调查局(U.S. Geological Survey)网站(http://glovis.usgs.gov/)的Landsat系列卫星遥感影像,整个县域需要两景影像覆盖,行带号分别为144/26、144/27,影像时间及传感器信息如表1所示。

本文所使用的每一景影像都包含有目前此类研究通用的一级标准数据产品(简称L1数据)以及经过校正和标准化处理的地表反射率数据产品(简称SR数据),用以定量研究传感器差异对反演结果的影响。

本文的研究对象为草场,因此需要对影像进行监督分类,提取出草场范围。首先,利用ENVI 5.1软件对2015年Landsat8 OLI的两景 L1影像(144/27、144/27)分别进行剪裁、辐射定标、融合以及FLAASH大气校正等预处理。其次初步将影像定义为林地、草地、荒地、水体、冰雪区五大类型,分别划定训练样本,通过最大似然法进行分类。经过分类后处理,以Google Earth Pro.的高分辨率影像为基础,划定验证样本,通过混肴矩阵计算分类精度。两景影像(144/27、144/27)的总体分类精度分别为97.7705%和98.8749%,Kappa系数分别为0.9692和0.9642。合并草地、荒地两种类型的区域,通过目视解译去除其中的耕地和建设用地区域,得到布尔津县草场分布范围(图2)。

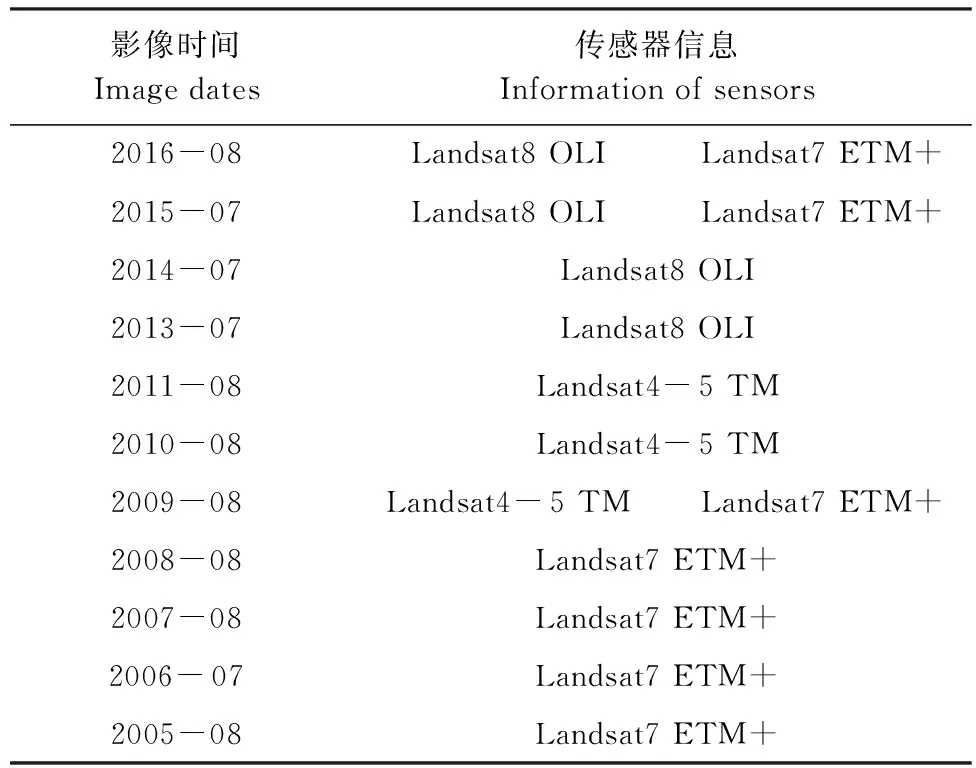
表1 遥感影像信息列表

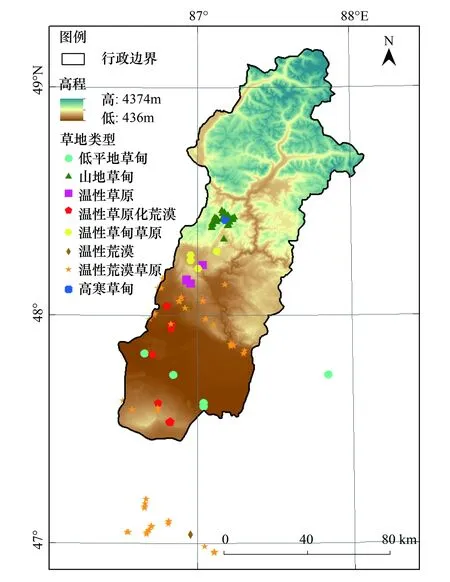
图1 研究区地形及监测点位分布图 Fig.1 Elevation and monitoring points′ distribution of study area

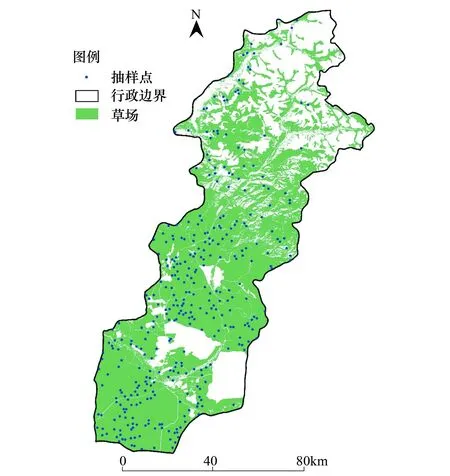
图2 草场范围及抽样点分布图 Fig.2 Distribution of grassland and sampling points in study area

3 研究方法

3.1 随机森林模型的建立与验证

3.1.1 植被指数选择

归一化植被指数(NDVI)是草场退化研究中使用最为广泛的植被指数[26- 28],本文首先选择其作为模型的解释变量之一。由于研究区南部大片区域为植被盖度较低的温性草原化荒漠、温性荒漠以及温性荒漠草原,仅使用NDVI作为解释变量,反演效果可能并不能达到预期,必须考虑土壤背景的影响[29],因此进一步引入可用于修正土壤背景敏感性以及气溶胶散射影响三个植被指数——土壤调节植被指数(SAVI)、修正土壤调节植被指数(MSAVI)、增强植被指数(EVI)。上述植被指数的计算方法如式1—式4所示,其中参数的选取依据了USGS发布的植被指数产品相关指南[30]。

(1)

(2)

(3)

(4)

3.1.2 模型建立

图1中监测点位的植被盖度数据分别来自2010、2011、2013、2014、2015年6—9月,经统计分析,在6—9月期间,植被盖度并无显著区别,因此在对应年份的6—9月中选择云量最少的影像加以利用,即利用2010—2011年8月的TM影像和2013—2015年7月的OLI影像计算相应点位的4个植被指数。

利用R软件在205组数数据(植被盖度及其对应植被指数)中随机抽取150组作为训练数据用于模型建立。

随机森林是由多棵相互没有关联的决策树组成的集成决策树,用{h(X,Θk),k=1, …}表示,其中X为输入向量,{Θk}为独立同分布随机向量[31]。与经典回顾分析类似,随机森林可以解释多个自变量(X1、X2…Xk)对因变量Y的作用。此处将植被盖度的实地监测值作为因变量Y,NDVI、SAVI、MSAVI和EVI作为自变量。随机森林模型的建立通过调用R语言中“randomForests”程序包[32]来实现。该方法首先完成两个随机采样过程,即通过自助法重采样技术有放回的在150组训练数据中重复随机抽取150个训练样本,未被抽取到的数据被称为“袋外”(out of bag)数据。再从NDVI、SAVI、MSAVI和EVI的4个变量中随机选择若干个变量(以mtry表示)建立决策树,模型中mtry的省缺值一般为总变量的1/3,本文有4个变量,则mtry值为1。最后重复n次上述过程，生成由n棵决策树组成的随机森林,n值越大预测越好。随着n值的增大,袋外数据误差在显著降低后会基本保持稳定。为了节省计算时间,n值保证袋外数据误差稳定即可,本文n值取150。

模型输出所有决策树计算结果的均值,并通过计算“解释方差百分比”来评定模型预测能力。对于各个自变量对因变量的影响程度,用方差增量以及节点纯度增量两个指标来定性表征。前者指将某一变量替换成随机变量后对预测结果造成的影响,若用于替换的随机变量显著改变了方差,则认为原变量重要性很高;后者从同质性增加的角度去表征变量的重要性[33]。随机森林模型的具体算法请参照Biau等[34]的文章。

为了将随机森林回归方法与传统的线性回归进行比较,本文采用同样的训练数据同时建立了植被盖度与NDVI、SAVI、MSAVI和EVI的一元线性回归及多元线性回归模型。

3.1.3 模型验证

利用205组数据经过随机抽样剩余的55组数据用于模型验证。应用前文建立的随机森林模型和各个线性回归模型分别计算55个点位的植被盖度预测值,并将实测值与预测值相减,根据差值分布情况比较模型的预测能力。此外,通过绘制残差散点图和正态Q-Q图来检验线性回归模型方差齐性以及残差的正态性,并通过Kappa系数来判断变量的共线性。

3.2 模型的应用及其不确定性分析

3.2.1 模型应用

利用ArcMap 10软件在研究区域内随机生成1000个相互间隔大于1km的点位,去除草场范围之外的点位,得到草场抽样点。为了研究模型在基于多源数据的植被盖度反演领域的应用,本研究以2005—2008年ETM+影像、2009—2011年TM影像、2013—2015年OLI影像为基础,分析2005—2015年间(除2012年),植被盖度的变化趋势。

首先,剔除研究时段内落在云层和云影中的草场抽样点,最终得到的356个点位用于本小节的抽样分析(图2)。其次,分别利用上述影像的L1和SR数据计算各个点位的NDVI、SAVI、MSAVI和EVI值,将其输入3.1中建立的随机森林模型,分别得到监测点位基于L1数据和SR数据的植被盖度值。最后,将每年356个监测点位的植被盖度预测值求平均,绘制出基于L1数据和SR数据的植被盖度变化趋势图。

3.2.2 不确定性分析

由于2005—2015年间遥感影像源自3个不同的传感器,而传感器的差异会给反演结果带来一定影响,因此本研究进一步应用下载自美国地质调查局地球资源观察和科学中心(Earth Resources Observation and Science Center)的MODIS—MOD13Q1 V005数据集建立随机森林模型,反演2005—2015年的植被盖度。由于MODIS数据不存在传感器差异问题,因此可将基于此数据反演出的植被盖度变化趋势作为参考,将3.2.1中得到的基于L1和SR数据的趋势曲线与之相比较,变化趋势越接近基于MODIS数据的反演结果,则说明该数据中不同传感器给反演结果造成的误差越小。

前文提到SR数据是L1数据经过校正和标准化处理的地表反射率数据产品,可在一定程度上克服传感器的差异对结果带来的影响。为了定量分析SR数据对反演结果的改进效果及不确定性,本研究进一步比对同一时期内,基于不同传感器的反演结果之间存在的差异。

研究区范围草场生长期内,同时具有TM和ETM+影像的时段是2009年8月,同时具有ETM+和OLI影像的时段是2015年7月和2016年8月。在草场抽样点中去除09、15、16年3年内云层、云影中的点位以及ETM+数据中坏条带中的点位后,剩余663个点位用于不确定分析。利用随机森林模型分别计算同一时段基于不同传感器的反演结果并相减,分别绘制基于L1数据和SR数据的TM—ETM+ 、OLI—ETM+的盖度反演结果差异概率密度图。

4 结果与讨论

4.1 拟合结果

随机森林模型的计算结果显示,基于L1数据和SR数据而建立的随机森林回归模型输出的解释方差百分比分别为69.82%和72.42%,因此后者的预测效果优于前者;重要性方面,各个植被指数并未表现出明显的差别(表2)。

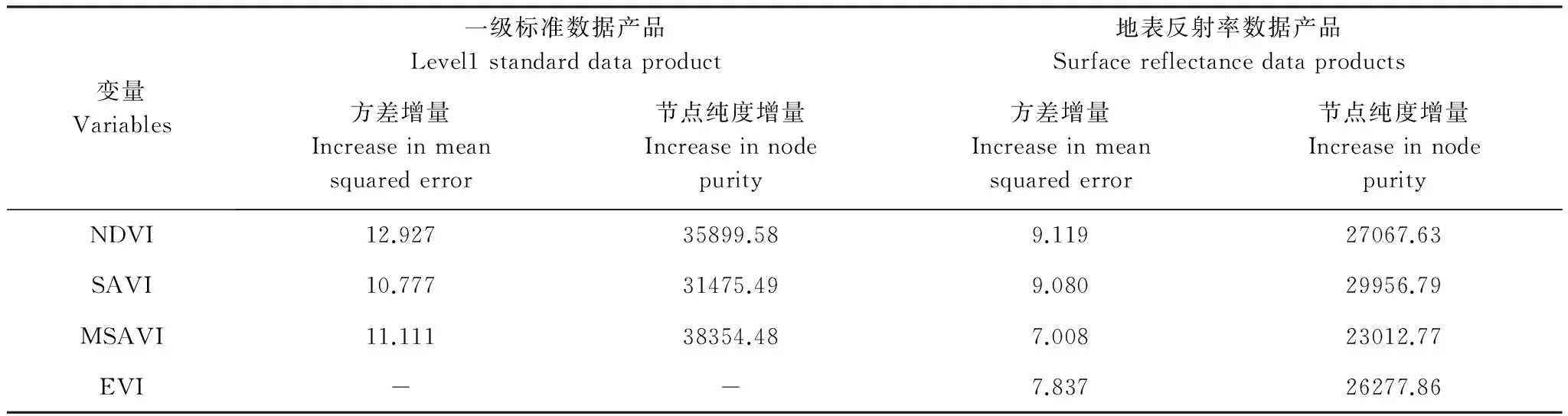
表2 随机森林回归模型变量重要性

由于L1数据未经过标准化处理,TM和OLI数据计算的EVI值不在同一数量级,无法用于模型的建立；NDVI：归一化植被指数,Normalized Difference Vegetation Index;SAVI：土壤调节植被指数,Soil Adjusted Vegetation Index;MSAVI：修正土壤调节植被指数,Modified Soil Adjusted Vegetation Index;EVI：增强植被指数,Enhanced Vegetation Index

本研究一共建立线性回归模型23个,其中P值显著的模型及相应参数如表3所示。由表3可知,对于一元线性回归模型来说L1数据和SR数据的R2差别不大;对于多元回归来说所有的L1数据都无法得到显著结果;从R2的数值上来看SR数据的多元回归的效果要明显优于一元回归。

4.2 模型比较

为了进一步分析上述模型的预测能力,本文将55个验证点位的监测值和预测值作差,结果的分布情况如图3所示。首先,虽然L1和SR数据的一元回归效果在表3中无法通过R2判断,但通过比较红色和绿色箱线图可明显看出,SR数据实测值和预测值的差异明显小于L1数据;第二,随机森林回归模型的预测能力略优于多元回归模型,且这两者明显优于一元线性回归;第三,所有线性回归的结果较真实值来说普遍偏小,但随机森林的预测偏差相对均衡。

在本文所建立的所有模型中,预测效果最好的是基于L1和SR数据的随机森林模型,以及由变量SAVI-MSAVI建立的SR数据二元回归模型。

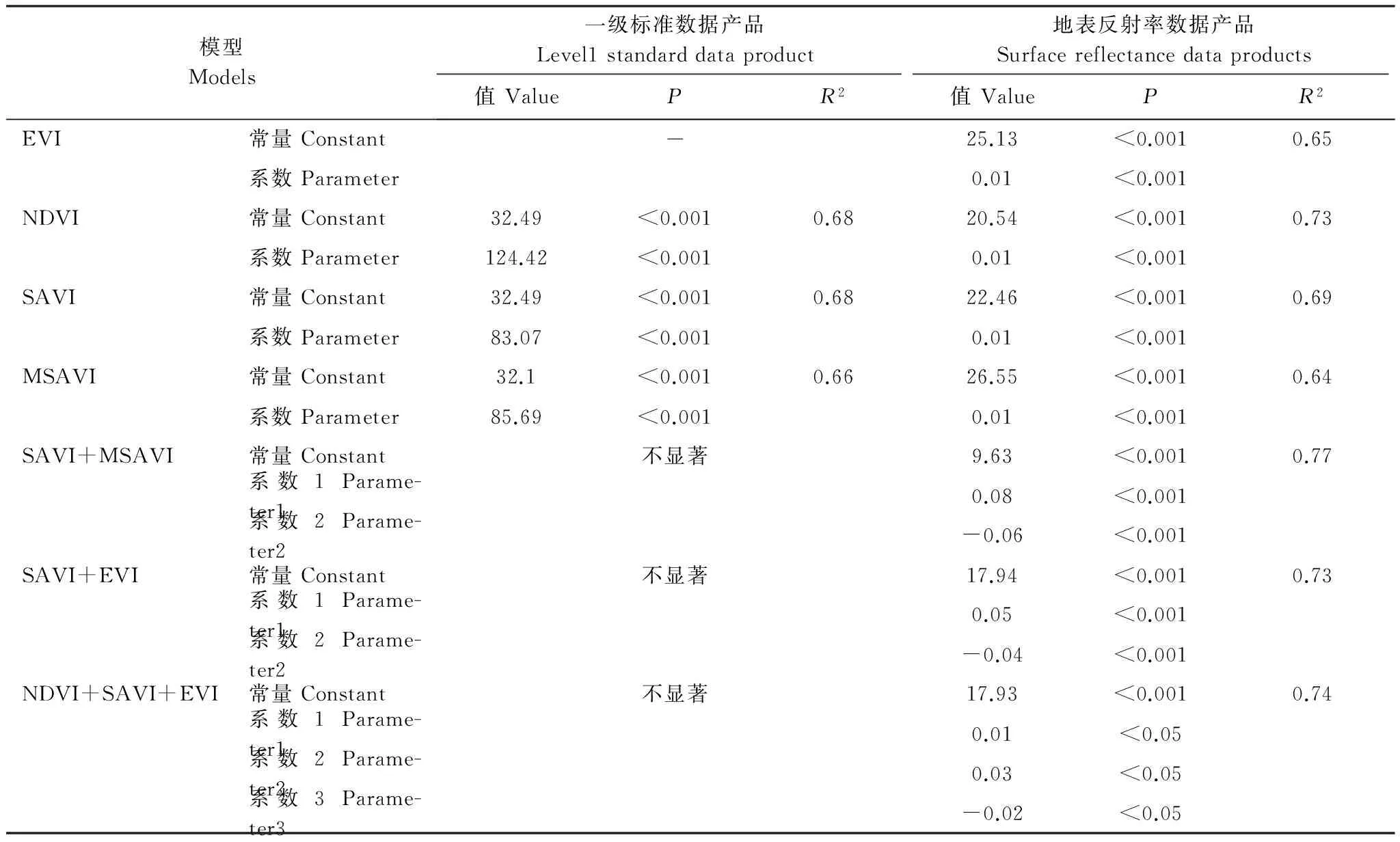
表3 线性回归模型结果

由于L1标准化处理,TM和OLI数据计算的EVI值不在同一数量级,无法用于模型的建立

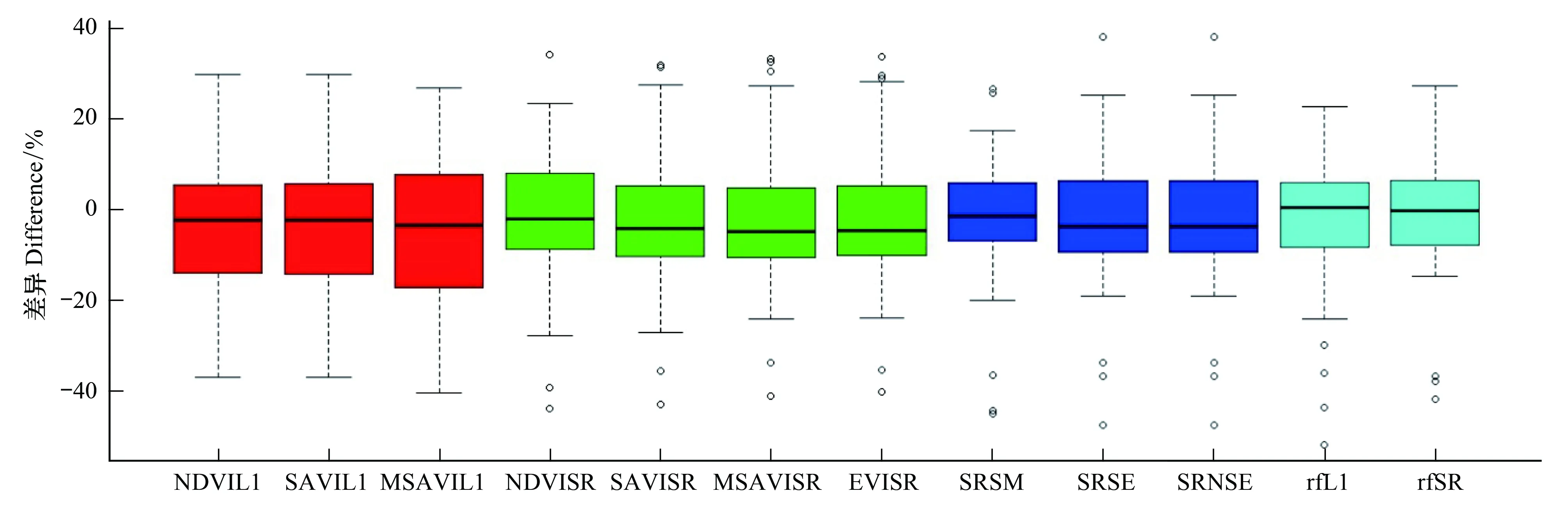
图3 植被盖度的实测值与预测值差异Fig.3 The difference between monitoring values and predicted valuesNDVIL1：基于L1数据NDVI指数的线性回归模型,Linear model based on NDVI from level 1 standard product;SAVIL1：基于L1数据SAVI指数的线性回归模型,Linear model based on SAVI from level 1 standard product; MSAVIL1：基于L1数据MSAVI指数的线性回归模型,Linear model based on MSAVI from level 1 standard product;NDVISR：基于SR数据NDVI指数的线性回归模型,Linear model based on NDVI from surface reflectance product;SAVISR：基于SR数据SAVI指数的线性回归模型,Linear model based on SAVI from surface reflectance product;MSAVISR：基于SR数据MSAVI指数的线性回归模型,Linear model based on MSAVI from surface reflectance product;EVISR：基于SR数据EVI指数的线性回归模型,Linear model based on EVI from surface reflectance product;SRSM：基于SR数据SAVI及MSAVI指数的线性回归模型,Linear model based on SAVI and MSAVI from surface reflectance product;SRSE：基于SR数据SAVI及EVI指数的线性回归模型,Linear model based on SAVI and EVI from surface reflectance product;SRNSE：基于SR数据NDVI、SAVI及EVI指数的线性回归模型,Linear model based on NDVI,SAVI and EVI from surface reflectance product;rfL1：基于L1数据的随机森林回归模型,Random forest model based on level 1 standard product;rfSR：基于SR数据的随机森林回归模型,Random forest model based on surface reflectance product

图4为SRSM方差齐性和残差正态性检验结果。理想状态下,残差-拟合值关系图上的点应随机分布,而正态QQ图中的点应分布于虚线之上,但SRSM模型并不能满足其基本假设条件,特别是残差的正态分布性。不仅如此,本研究所有其他的线性回归模型也都不能很好的满足其基本假设。此外,SRSM的各变量应满足非共线性,即Kappa值小于100,但经过计算该模型的Kappa值高达5570。从对模型的诊断结果看,SRSM模型虽然预测效果较好,但应用于植被盖度的反演存在较大的缺陷。

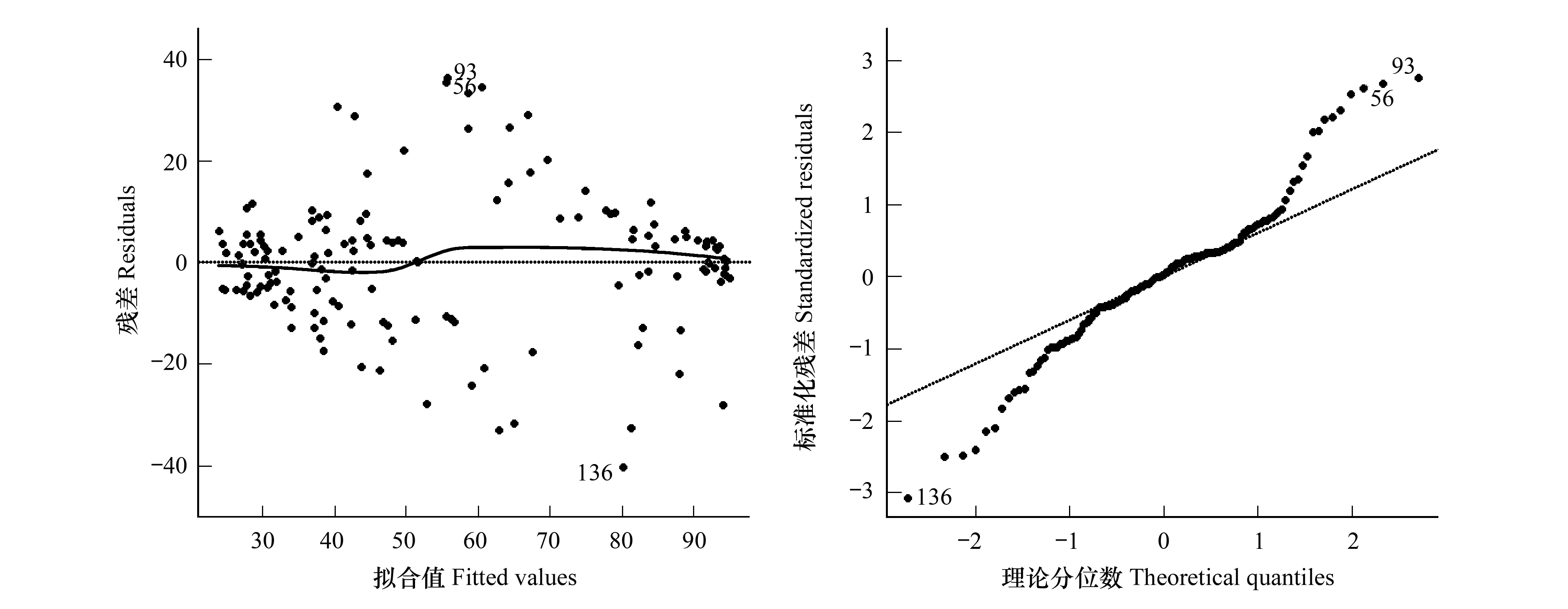
图4 SRSM模型的假设检验 Fig.4 Hypotheses testing of SRSM modelSRSM：基于SR数据SAVI及MSAVI指数的线性回归模型,Linear model based on SAVI and MSAVI from surface reflectance product

综上,本文认为随机森林模型相较于线性回归模型来说不但不受诸多假设条件和非共线性要求的制约,并能达到更好的预测效果,因此更适合作为植被盖度的反演模型。

4.3 2005—2015年草场植被盖度变化趋势及不确定性分析

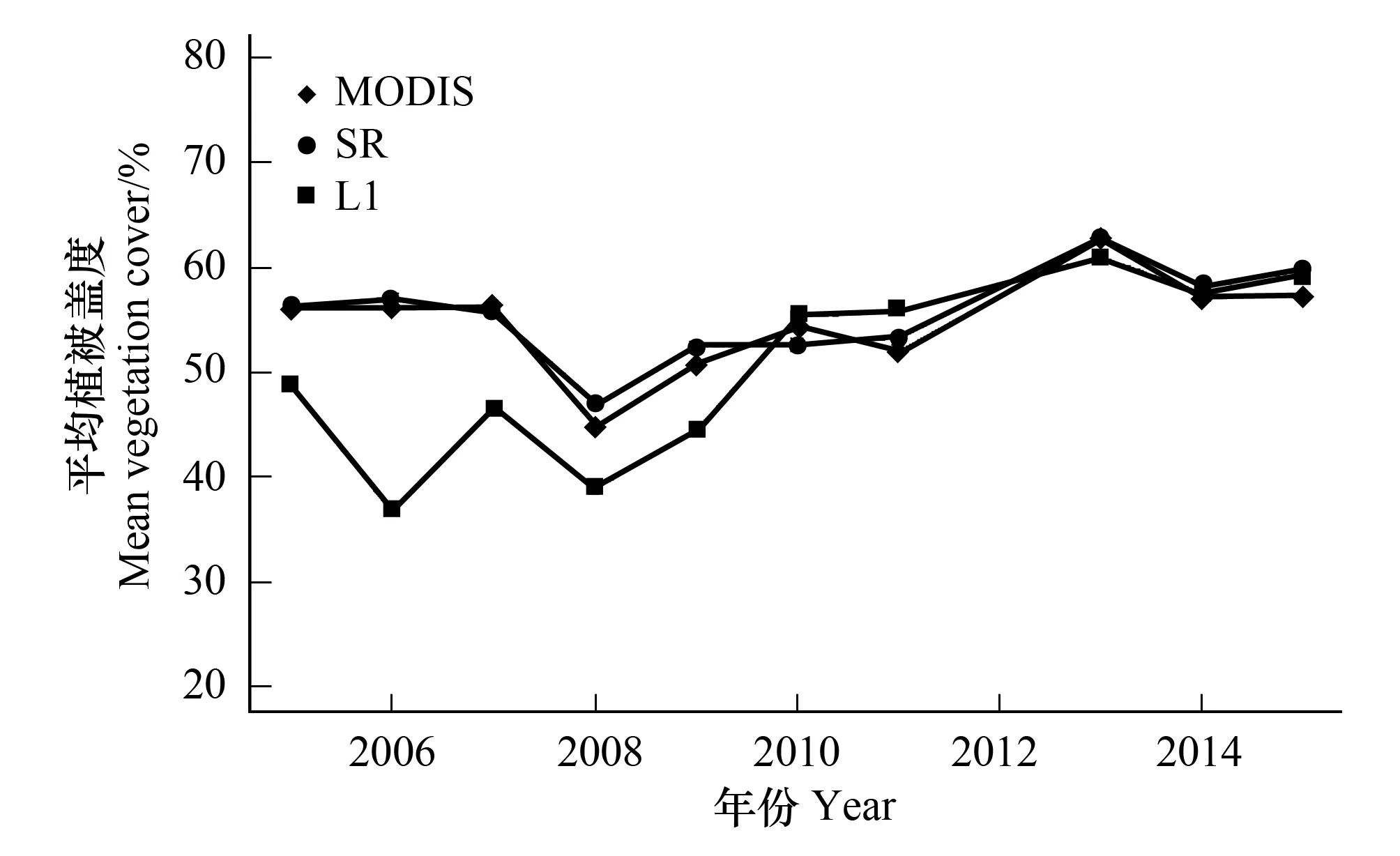
图5 基于MODIS、SR及L1数据的抽样点盖度平均值 Fig.5 Mean vegetation cover of sampling points based on MODIS, SR and L1 data L1： 一级标准数据产品Level1 Standard Data Product;SR: 经过校正和标准化处理的地表反射率数据产品Surface Reflectance Data Products,

基于L1、SR以及MODIS数据分别得到的草场盖度平均值变化趋势如图5所示。除2006年之外,SR和L1数据反演得到的植被盖度变化情况基本保持了一致的变化趋势,但2005—2009年,也即数据源为ETM+的时间段内,基于L1的反演结果要明显小于SR数据的反演结果。SR数据与不存在传感器差异问题的MODIS数据反演所得的植被盖度值相比,差异小于5%,但L1数据的偏差较大,ETM+数据的预测结果普遍偏小,2006年的植被盖度均值甚至偏小超过20%。

为了分析传感器差异给反演结果造成的影响,本文进一步对比了同一时期内源自不同传感器光谱信息反演得到的植被盖度,对比结果如图6所示。该图显示了2009年ETM+数据与TM数据,以及2015—2016年ETM+数据与OLI数据分别反演得到的植被盖度的差异。

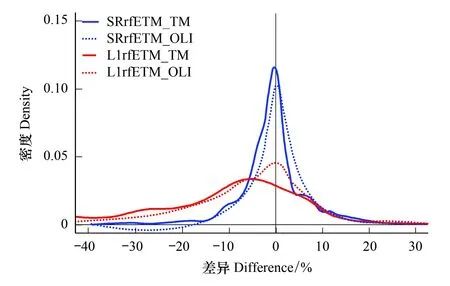
图6 同时段不同数据源的预测结果差异 Fig.6 Difference in predicted values based on different dada sources in the same periodSRrfETM_TM：SR数据基于ETM+传感器与TM传感器随机森林反演结果的差异;SRrfETM_OLI：SR数据基于ETM+传感器与OLI传感器随机森林反演结果的差异;L1rfETM_TM：L1数据基于ETM+传感器与TM传感器随机森林反演结果的差异;L1rfETM_OLI：L1数据基于ETM+传感器与OLI传感器随机森林反演结果的差异

由图6的概率密度曲线可知,同一时段L1数据不同传感器对计算结果差异巨大,特别是ETM+数据的预测结果普遍小于TM数据,上述结果与图5的结论一致。从具体计算的数值来看：对于SR数据,几乎90%的测试点位上不同传感器对计算结果产生的影响都能落在(-10%,11%)的区间之中;但对于L1数据,90%测试点位的ETM+与OLI的差异落在(-30%,11%)范围内,而ETM+与TM的差异更是落在了(-40%,9%)之中。由此可见,不同传感器的差异在L1数据上表现的尤为突出,该数据不适于基于多元数据的草场植被盖度变化趋势研究,即便是经过校正以及标准化处理的SR数据,反演结果也存在约±10%的不确定性。

4.4 讨论

就反演方法而言,以往类似的研究多基于相关分析线性回归以及多项式模型[16- 17,35- 37],且模型的筛选通常仅仅通过P值以及决定系数R2来评判，而不对模型预测结果做进一步验证。从本文的线性回归结果看,L1数据和SR数据的一元线性模型都具有显著性且R2水平相当,在以MSAVI作为解释变量时,L1数据的拟合效果甚至要优于SR数据(表3)。但从图3中可以清楚地看到前者的误差要远远大于后者。可见,P值以及R2并未帮助研究者对比出SR数据的优越性。更为重要的是,上述模型都属于参数估计类,若不对其基本假设进行验证,就无法保证所得结论的可靠性。本研究显示,所有的线性模型都未能通过方差齐性和残差正态性检验。而遗憾的是,迄今大多数研究都忽略了这种统计学的基本要求。

需要强调的是,除了模型本身之外,数据源也是影响预测效果的重要因素。由图5中基于MODIS数据反演得到的变化趋势可知,近10年来草场盖度的平均值总的变化幅度不足20%左右,而2006年L1数据反演所得之盖度平均值与MODIS数据计算结果的偏差就已经超过了20%。该问题在图6中体现得更加突出。这便意味着,传感器差异带来的影响甚至可能超过草场变化本身。虽然本研究所用的SR数据与传统研究常用的L1数据相比,已经在一定程度是减少了这类影响[38],但仍未将其完全消除。因此,在涉及长时间序列草场植被变化以及驱动力的研究中,对这种影响进行量化就显得尤为必要。

本文的局限性主要体现在以下几个方面：首先,使用的实地监测数据为1m×1m样方的测量值,而遥感影像为30m×30m精度,如果监测点周围数10m范围内不能保持均一性,拟合结果会因此受到影响;其次,本研究所涉及的草场种类众多,但植被指数计算涉及的参数均采用了USGS网站提供产品指南中的推荐值,后续研究中应对不同类型草场分别设定参数,以提高结果的可靠程度;再次,本研究初步估算了2005—2015年草场盖度的平均值,今后可进一步应用随机森林模型分析草场植被盖度的空间变化特征;最后,本文仅初步研究了传感器差异给反演结果造成的影响,如何通过归一化处理等方法减小这种差异将是未来研究中需要探索的问题。

5 结论

1) 本文通过随机森林回归方法建立了基于Landsat系列卫星数据的草场植被盖度反演模型,并应用该模型分析了近10年来布尔津县草场盖度的变化趋势。

2) 通过与线性回归反演模型的对比可知,随机森林回归方法不但能规避线性回归苛刻的假设条件,同时可超越绝大多数线性回归模型的预测能力。

3) 模型不确定性方面,Landsat ETM+的标准数据反演得到的植被盖度较之TM和OLI数据普遍偏小;地表反射率数据虽然可以大幅降低Landsat系列不同传感器对反演结果的影响,但反演得到的植被盖度仍存在(-10%,11%)的不确定性。

致谢：北京大学生命科学学院王昊老师提供MODIS数据,中国环境科学研究院张玉波博士和付刚在遥感影像处理方面给予帮助,大理大学东喜马拉雅资源与环境研究所任国鹏老师为本研究提出建议,特此致谢。

参考文献(References):

[1] 樊江文, 钟华平, 陈立波, 张文彦. 我国北方干旱和半干旱区草地退化的若干科学问题. 中国草地学报, 2007, 29(5): 95- 101.

[2] 黄敬峰, 桑长青. 天山北坡中段天然草场牧草产量遥感动态监测模式. 干旱区资源与环境, 1993, 7(2): 53- 59.

[3] 李京, 陈晋, 袁清. 应用NOAA/AVHRR遥感资料对大面积草场进行产草量定量估算的方法研究. 自然资源学报, 1994, 9(4): 365- 368.

[4] Hmimina G, Dufrêne E, Pontailler J Y, Delpierre N, Aubinet M, Caquet B, De Grandcourt A, Burban B, Flechard C, Granier A, Gross P, Heinesch B, Longdoz B, Moureaux C, Ourcival J M, Rambal S, Saint André L, Soudani K. Evaluation of the potential of MODIS satellite data to predict vegetation phenology in different biomes: an investigation using ground-based NDVI measurements. Remote Sensing of Environment, 2013, 132: 145- 158.

[5] Geerken R, Batikha N, Celis D, DePauw E. Differentiation of rangeland vegetation and assessment of its status: field investigations and MODIS and SPOT VEGETATION data analyses. International Journal of Remote Sensing, 2005, 26(20): 4499- 4526.

[6] Chen S B, Rao P. Land degradation monitoring using multi-temporal Landsat TM/ETM data in a transition zone between grassland and cropland of northeast China. International Journal of Remote Sensing, 2008, 29(7): 2055- 2073.

[7] Feng Y, Lu Q, Tokola T, Liu H, Wang X. Assessment of grassland degradation in Guinan county, Qinghai Province, China, in the past 30 years. Land Degradation & Development, 2009, 20(1): 55- 68.

[8] Geerken R, Zaitchik B, Evans J P. Classifying rangeland vegetation type and coverage from NDVI time series using Fourier Filtered Cycle Similarity. International Journal of Remote Sensing, 2005, 26(24): 5535- 5554.

[9] Cai H Y, Yang X H, Xu X L. Human-induced grassland degradation/restoration in the central Tibetan Plateau: the effects of ecological protection and restoration projects. Ecological Engineering, 2015, 83: 112- 119.

[10] Wessels K J, Prince S D, Carroll M, Malherbe J. Relevance of rangeland degradation in semiarid northeastern South Africa to the nonequilibrium theory. Ecological Applications, 2007, 17(3): 815- 827.

[11] 魏小琴. 阿勒泰地区NDVI变化及其主要驱动因子分析[D]. 乌鲁木齐: 新疆农业大学, 2015.

[12] Röder A, Udelhoven T, Hill J, Del Barrio G, Tsiourlis G. Trend analysis of Landsat-TM and -ETM+ imagery to monitor grazing impact in a rangeland ecosystem in Northern Greece. Remote Sensing of Environment, 2008, 112(6): 2863- 2875.

[13] Li J Y, Yang X C, Jin Y X, Yang Z, Huang W G, Zhao L N, Gao T, Yu H D, Ma H L, Qin Z H, Xu B. Monitoring and analysis of grassland desertification dynamics using Landsat images in Ningxia, China. Remote Sensing of Environment, 2013, 138: 19- 26.

[14] 杨强, 王婷婷, 陈昊, 王运动. 基于MODIS EVI数据的锡林郭勒盟植被覆盖度变化特征. 农业工程学报, 2015, 31(22): 191- 198.

[15] 吕长春, 王忠武, 钱少猛. 混合像元分解模型综述. 遥感信息, 2003, (3): 55- 58, 60- 60.

[16] 郭辉, 黄粤, 李向义, 包安明, 宋洋, 孟凡浩. 基于多尺度遥感数据的塔里木河干流地区植被覆盖动态. 中国沙漠, 2016, 36(5): 1472- 1480.

[17] 马中刚, 孙华, 王广兴, 林辉, 佘宇晨, 邹琪. 基于Landsat 8-OLI的荒漠化地区植被覆盖度反演模型研究. 中南林业科技大学学报, 2016, 36(9): 12- 18.

[18] 李欣海. 随机森林模型在分类与回归分析中的应用. 应用昆虫学报, 2013, 50(4): 1190- 1197.

[19] Cutler D R, Edwards Jr T C, Beard K H, Cutler A, Hess K T, Gibson J, Lawler J J. Random forests for classification in ecology. Ecology, 2007, 88(11): 2783- 2792.

[20] 金宇, 周可新, 方颖, 刘欣. 基于随机森林模型预估气候变化对动物物种潜在生境的影响. 生态与农村环境学报, 2014, 30(4): 416- 422.

[21] 王盼, 陆宝宏, 张瀚文, 张巍, 孙银凤, 季妤. 基于随机森林模型的需水预测模型及其应用. 水资源保护, 2014, 30(1): 34- 37, 89- 89.

[22] Rodríguez-Veiga P, Wheeler J, Louis V, Tansey K, Balzter H. Quantifying forest biomass carbon stocks from space. Current Forestry Reports, 2017, 3(1): 1- 18.

[23] Mansour K, Mutanga O. Classifying increaser species as an indicator of different levels of rangeland degradation using WorldView- 2 imagery. Journal of Applied Remote Sensing, 2012, 6(1): 063558.

[24] Chander G, Markham B L, Helder D L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO- 1 ALI sensors. Remote Sensing of Environment, 2009, 113(5): 893- 903.

[25] Vogelmann J E, Gallant A L, Shi H, Zhu Z. Perspectives on monitoring gradual change across the continuity of Landsat sensors using time-series data. Remote Sensing of Environment, 2016, 185: 258- 270.

[27] Pattison R R, Jorgenson J C, Raynolds M K, Welker J M. Trends in NDVI and tundra community composition in the arctic of NE Alaska between 1984 and 2009. Ecosystems, 2015, 18(4): 707- 719.

[28] 毛志春, 宋宇, 李蒙蒙. 基于MODIS反演数据的河套地区荒漠化研究. 北京大学学报: 自然科学版, 2015, 51(6): 1102- 1110.

[29] Liu B, You G Y, Li R, Shen W S, Yue Y M, Lin N F. Spectral characteristics of alpine grassland and their changes responding to grassland degradation on the Tibetan Plateau. Environmental Earth Sciences, 2015, 74(3): 2115- 2123.

[30] USGS. Landsat surface reflectance-derived spectral indices, Version 3.3. 2016. [2016- 12- 13] https://landsat.usgs.gov/sites/default/files/documents/si_product_guide.pdf

[31] Breiman L. Random forests. Machine Learning, 2001, 45(1): 5- 32.

[32] Liaw A, Wiener M. Classification and regression by randomForest. R News, 2002, 2(3): 18- 22.

[33] Echeverry-Galvis M A, Peterson J K, Sulo-Caceres R. The social nestwork: tree structure determines nest placement in Kenyan weaverbird colonies. PLoS One, 2014, 9(2): e88761.

[34] Biau G, Scornet E. A random forest guided tour. TEST, 2016, 25(2): 197- 227.

[35] Brinkmann K, Dickhoefer U, Schlecht E, Buerkert A. Quantification of aboveground rangeland productivity and anthropogenic degradation on the Arabian Peninsula using Landsat imagery and field inventory data. Remote Sensing of Environment, 2011, 115(2): 465- 474.

[36] 万红梅, 李霞, 董道瑞. 基于多源遥感数据的荒漠植被覆盖度估测. 应用生态学报, 2012, 23(12): 3331- 3337.

[37] 董建军, 牛建明, 张庆, 康萨如拉, 韩芳. 基于多源卫星数据的典型草原遥感估产研究. 中国草地学报, 2013, 35(6): 64- 69.

[38] Claverie M, Vermote E F, Franch B, Masek J G. Evaluation of the Landsat- 5 TM and Landsat- 7 ETM+ surface reflectance products. Remote Sensing of Environment, 2015, 169: 390- 403.