2.5MW风电齿轮箱轴承疲劳寿命研究

汪东恒， 陈文华， 杨帆， 贺青川， 潘骏， 潘晓东

（1.浙江理工大学浙江省机电产品可靠性技术研究重点实验室，杭州 310018；2.杭州前进齿轮箱集团股份有限公司，杭州 311203）

0 引言

风电齿轮箱是风力发电机的核心部件之一，因常年工作在较恶劣的自然环境中，加之所承受载荷的随机性和交变性，使其成为可靠性相对较低的部件之一。据统计，齿轮箱故障所占比例约为9.8%，但因齿轮箱故障造成的停机时间占比高达19.4%。对于齿轮箱，由于轴承失效引起的故障比例约为19%，仅次于齿轮失效[1-3]。因此研究变载荷条件下轴承的疲劳寿命，对实现齿轮箱的可靠性设计以及故障的预防和发生有着重要的参考意义。

目前对风电轴承疲劳寿命的预测，主要采用名义应力法与线性Miner疲劳累积损伤理论相结合的方法。毛俊超等[4]运用Miner线性疲劳累积损伤理论和雨流计数方法，得到风力机主轴轴承载荷谱，并计算了低速轴轴承的疲劳寿命。周志刚等[5]对风力机齿轮传动系统进行了齿轮-轴承耦合动力学研究和动态可靠性分析，并根据得到的疲劳载荷谱，使用修正的Miner线性累积损伤理论建立了关键零件的疲劳寿命预测模型，对系统各齿轮和轴承的疲劳寿命进行了估算。李会川[6]用普通轴承代替风电轴承进行加速疲劳寿命试验，找到了一种估算风电轴承载荷谱Miner线性损伤累积理论修正系数的方法，并针对风电轴承的高可靠性要求，对实际载荷谱进行等效实验，确定了修正系数。AN Zongwen等[7]通过ANSYS软件，对风力发电机主轴轴承在不同载荷工况下的接触应力进行分析，并采用名义应力法和Miner线性疲劳累积损伤理论，对轴承寿命进行预测。然而包括上述文献在内的许多研究在使用Miner理论进行疲劳寿命估计时，大多选用恒幅循环应力或者多级恒幅循环应力作为计算依据，并未考虑应力的随机性。

本文基于名义应力法和Miner线性疲劳累积损伤理论，对变载荷条件下的风电齿轮箱轴承寿命进行了研究。首先运用修正的Miner疲劳累积损伤理论建立了风电齿轮箱轴承的疲劳寿命计算模型；其次运用MATLAB数值分析软件对风场测得的齿轮箱离散载荷谱作了进一步统计分析处理，获得了精度更高的连续载荷谱，该载荷谱更加符合真实情况。在对齿轮箱进行受力分析的基础上，以占故障比例较高的高速轴（即输出轴）轴承为例，对齿轮箱轴承疲劳寿命进行了计算。本文方法充分考虑了载荷的随机性特点，所预测的轴承疲劳寿命结果更合理准确。

1 风电齿轮箱结构、参数和载荷谱

1.1 风电齿轮箱结构和主要参数

图1为2.5 MW风电齿轮箱结构简图，共由三级齿轮传动组成。第一级为定轴轮系，由齿轮1、2、3组成；第二级为差动轮系，由齿轮4、5、6和行星架K组成；第三级为平行轴齿轮传动。齿轮箱输入端载荷为转矩，输入功率分两路传递，第一路由齿轮1经定轴轮系传递至齿轮4，第二路由行星架传递至齿轮5，最后在齿轮6处汇合后经第三级传递至输出端，传动比为1:86.1。

各齿轮齿数如下：Z1=142、Z2=37、Z3=66、Z4=138、Z5=55、Z6=26、Z7=131、Z8=27。第一、二级为直齿轮传动，压力角25°，模数11.25 mm；第三级为斜齿轮传动，压力角25°，螺旋角12.5°，模数7.95 mm。

图1 2.5 MW风电齿轮箱结构简图

1.2 齿轮箱输入载荷谱处理

载荷谱是否符合实际情况对疲劳计算结果的准确与否有很大的决定作用。图2是风场测得的齿轮箱输入轴20 a转矩-转数载荷数据，为经过雨流计数法得到的离散载荷谱。图中负值的转矩表示风力发电机叶片反转的情形，其循环次数较小，且无实际意义，故忽略不计，所以载荷谱实际有效工况为85级，范围为15～2535kN·m。

考虑到真实情况下风载的随机性，实际风载应该为连续的随机过程，所测载荷数据与真实风载间必定存在误差，所以有必要对其进行进一步统计分析处理，以获得精度更高的载荷谱。

将原始载荷数据中第一个转矩15 kN·m所对应的转数视为在0～30 kN·m上服从均匀分布，将第二个转矩45 kN·m所对应的转数视为在30～60 kN·m上服从均匀分布，依此类推，最后一个转矩2535 kN·m所对应的转数视为在2520～2550 kN·m上服从均匀分布。在用MATLAB试算时发现，把每个区间20等分，并把每个区间对应的转矩总转数平均分配到这20个端点上最为合适，如图3所示。85个工况一共可得到1700个点，调用lsqcurvefit函数对这1700个点进行曲线拟合，得到齿轮箱的连续载荷谱曲线，该曲线保证了各个区间积分后总转数约等于原载荷数据对应的转数，如图4所示。拟合曲线类型选择为高斯拟合，拟合优度判定系数R2=0.9898。

图2 风场20 a载荷数据

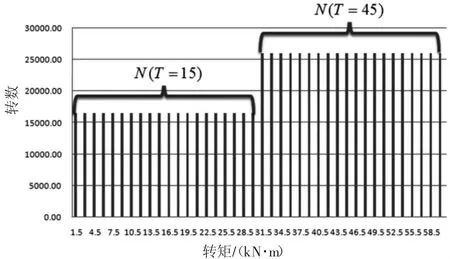
图3 载荷数据处理方法

图4 齿轮箱输入载荷谱

2 轴承疲劳寿命计算模型

根据Miner线性疲劳累积损伤理论，若结构破坏前所承受载荷由σ1、σ2、…σn等n个不同的应力水平组成，各应力水平下的疲劳寿命分别为N1、N2、…Nn，各应力下的循环数分别为n1、n2、…nn，则总的损伤量为

在Miner理论中，小于疲劳寿命极限的应力循环通常不被考虑，但实际上在风力发电机齿轮传动系统中，小于疲劳极限值的应力频次如果很高也会引起构件的疲劳损伤，因此需要对Miner理论对数形式的S-N曲线的水平线进行修正。如图5所示的EM（Elementary Miner）线和MM（Modified Miner）线为对OM（Original Miner）线的修 正 ，Se为疲劳寿命极限应力。本文使用EM线对轴承进行疲劳寿命估算。

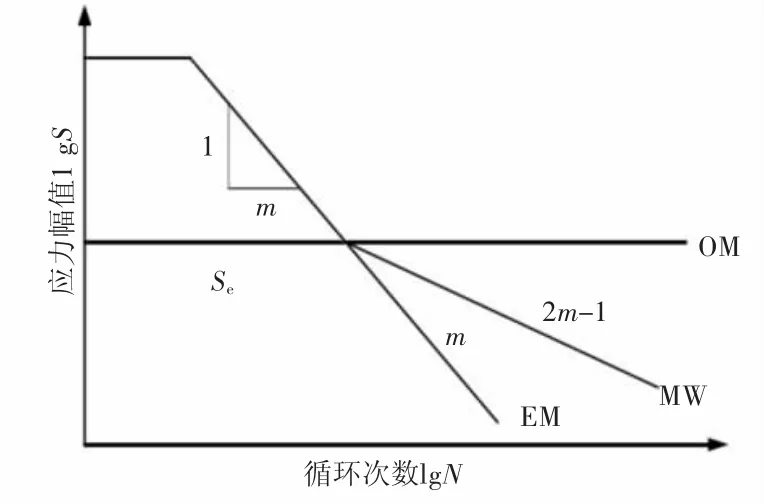
图5 S-N曲线修正

设轴承所承受的载荷依次为P1、P2、…、Pn，轴承在载荷Pi作用下实际循环次数为zi′，达到极限时的循环次数为zi，则根据Miner疲劳累积损伤理论，轴承在所有载荷下的总损伤为

图6 变载荷作用与寿命

式（2）是离散应力作用下的情况，根据积分思想，可以推出应力值连续变化情况下的累积损伤表达：

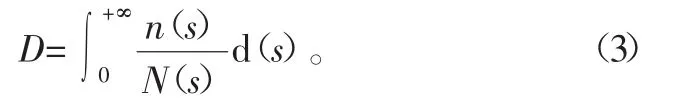
式中：n（s）、N（s）分别表示应力值为s时的实际循环数和破坏循环数，均为s的连续函数[8]。本文中N（s）为滚动轴承修正额定寿命Lna。

在得到轴承损伤后，可求出轴承使用寿命为

式中，T为所有载荷的作用总时间。

3 轴承当量动载荷计算

3.1 齿轮转矩分析

根据机械原理[9]和机械设计[10]相关知识，可计算出各级齿轮转矩为：

3.2 高速轴轴承当量动载荷计算

高速轴轴承NU2232、NU2234和QJ234主要承受输出轴从动齿轮所受圆周力、径向力和轴向力。其中左端NU2232和右端NU2234承受径向力，右端四点接触球轴承QJ234只承受轴向力[11]。受力的大小和方向可以根据斜齿轮传动的特点进行判断和计算。受力示意图如图7所示。

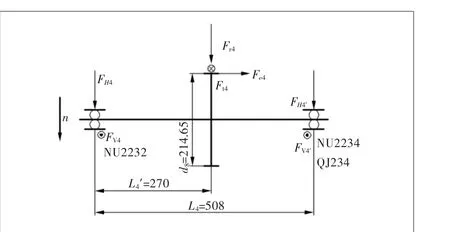
图7 高速轴轴承受力示意图

式中，X、Y分别为径向载荷系数、轴向载荷系数，查轴承手册[12]可知。fp为载荷修正系数，见表1，本文取fp=1.1。

表1 载荷系数fp

图8 轴承NU2232当量动载荷谱

以轴承NU2232为例，在MATLAB中计算出其当量动载荷谱，如图8所示。

4 轴承疲劳寿命计算

4.1 滚动轴承修正额定寿命公式

国际标准组织以Lundberg-Palmgren理论为基础，制定了滚动轴承的修正额定寿命计算公式为

式中：Lna为失效概率为n时的寿命；C为基本额定动载荷，N；P为当量动载荷，N；ε为寿命指数，球轴承取3，滚子轴承取10/3；a1为可靠性系数，见表2；a23为综合修正系数，包含材料性能系数a2和工作条件系数a3的综合影响[12]。

表2 可靠度与修正系数a1的对应值

大量的经验数据表明综合修正系数a23的取值跟轴承润滑条件紧密相关，根据经验，一般运行条件下，可以取1；当油液黏度较低，润滑条件较差时可取0.2，当润滑条件优越，足以在轴承滚动接触表面形成弹性流体动压油膜时，可以取2[13-15]。风电齿轮箱常年工作在野外，环境条件较恶劣，但是它有一套完整高效24 h运行的润滑系统，能根据齿轮箱工作状况自动调整油液循环、供给、温度和压力等，使齿轮箱始终保持良好的润滑状况，所以其运行条件与综合修正系数a23的关系还有待于进一步深入研究。本文暂取a23=1来计算轴承的寿命。

4.2 高速轴轴承疲劳寿命计算

1）蒙特卡罗方法的运用。

蒙特卡罗方法是一种随机模拟技术，又称统计模拟法、随机抽样法。它基于概率和统计理论方法原理，是一种使用随机数来解决计算问题的新方法。它将一定的概率模型应用到所要求解的问题中，通过计算机编程进行统计抽样或模拟来获得问题的近似解。

2）疲劳寿命计算。

根据式（3）得到轴承损伤后，可求出轴承可靠度0.9的疲劳寿命为

进而根据表2求出可靠度0.99的轴承寿命。算得该轴承疲劳寿命为27.53 a。

该计算结果所依据载荷谱为转矩载荷谱，而实际上影响轴承寿命因素很多。例如，轴承安装精度和所受瞬时振动冲击会使轴承承受一定的轴向力和倾覆力矩，工作温度、润滑、材料等因素与综合修正系数a23有密切关系，所以轴承的实际寿命和计算寿命可能会产生一定偏差。上述因素对轴承寿命的影响还有待于进一步研究。

5 结论

1）基于Miner疲劳损伤累积理论建立了变载荷条件下风电齿轮箱轴承的疲劳寿命计算模型。

2）充分考虑了风载的随机性特点，对风场实测的离散载荷数据做了进一步统计分析处理，得到了更精确更符合真实情况的齿轮箱连续载荷谱，为准确计算轴承的疲劳寿命作基础。

3）将轴承载荷和疲劳寿命计算相关公式中的参数视为正态随机变量，将蒙特卡洛随机抽样法应用到计算中，使轴承疲劳寿命计算结果更符合实际情况。在一般运行条件下，算得NU2232轴承99%可靠度的疲劳寿命为27.53 a。

［参考文献］

[1] CRABTREE C J,FENG Y,TAVNER P J.Detecting incipient wind turbine gearbox failure:a signal analysis method for onlineconditionmonitoring[C]//ProceedingsofEuropeanWindEnergy Conference(EWEC 2010).2010:20-23.

[2] 李龙.兆瓦级风电齿轮箱的疲劳可靠性研究[D].杭州:浙江理工大学,2014.

[3] 郑朝朋.2.5MW风电齿轮箱可靠性分析[D].杭州:浙江理工大学,2015.[4] 毛俊超,邓甲红,马浩然.2MW风力发电机低速轴轴承寿命分析[J].机械设计与制造,2014(2):206-208.

[5] 周志刚.随机风作用下风力发电机传动系统动力学及动态可靠性研究[D].重庆:重庆大学,2012.

[6] 李会川.风电轴承损伤累积修正系数试验研究[D].大连：大连理工大学,2014.

[7] LIANG Yong,AN Zongwen,LIU Bo,et al.Fatigue life prediction for wind turbine main shaft bearings[C]//International Conference on Quality,Reliability,Risk,Maintenance,and Safety Engineering.2013:930-935.

[8] 张畅.抓斗卸船机关键零部件载荷谱及寿命评估[D].上海:上海交通大学,2010.

[9] 孙桓,陈作模,葛文杰.机械原理[M].8版.北京:高等教育出版社,2013.

[10] 濮良贵,纪名刚.机械设计[M].7版.北京:高等教育出版社,2005.

[11]廖雅诗.某型直升机滚动轴承疲劳寿命预测及其可靠性分析方法[D].长沙:中南大学,2014.

[12] 张松林.最新轴承手册[M].北京:电子工业出版社,2007.

[13]杨洁,张晓东.滚动轴承寿命计算方法的应用和分析[J].石油机械,2004,32(5):27-29.

[14] 王勇.滚动轴承寿命计算[J].电机控制与应用,2009,36(7):14-18.

[15]于宏伟.轴承的理论寿命和修正寿命计算方法浅论[J].精密制造与自动化,2009(7):14-18.