等边布置四方柱绕流涡脱落规律的数值研究

王圣洁，张 伟，刘 欢

（天津城建大学 能源与安全工程学院 天津 300384）

流体流过多个柱体的绕流现象，在诸多工程领域都有涉及，例如桥梁的支柱与吊索或者成群排列的换热器等都涉及典型的多柱体绕流问题.其中四等边方柱的绕流，作为较为常见的单元，有着重要的研究意义.

单方柱绕流问题因为流动简单、流动现象丰富，经常被作为湍流模型的标准验证算例[1].因此，目前国内外的相关研究大多集中于单方柱的绕流，对于多方柱的绕流研究相对较少涉及.就多柱体绕流而言，研究者们似乎对于多圆柱绕流问题给与了更多的关注，也取得了很多研究成果.张爱社等[2]对等直径四圆柱在雷诺数Re=200时的绕流特性进行了探究.张鹏飞等[3]针对三圆柱的绕流问题，在雷诺数Re=200时的各种流场特性进行了实验和数值研究.Farrant等[4]对四圆柱和双圆柱的绕流问题进行研究，结果表明四圆柱与双圆柱在绕流特性与流场阻力方面有明显不同.李景银等[5]针对雷诺数Re=100、间距比等于4条件下的正方形排列四圆柱绕流现象进行了研究.Lam等[6]采用数值方法对二维和三维四圆柱流场流动及动力学特性进行研究.近几年，一些学者也陆续开展了对于多方柱绕流问题的研究，Shams等[7]采用LBM方法对低雷诺数下四等边方柱的绕流进行了数值模拟，但对于漩涡脱落的规律，未得出精确的结果.赵心广[8]和张伟等[9]分别对较高雷诺数（Re=8×104）和低雷诺数（Re=100）的三方柱绕流问题进行了数值研究.因为方柱有四个拐角而与圆柱的几何特征不同，所以无论是绕流流场特性还是流体动力特性，两者都有很大的差别.为了更加全面地了解方柱群的绕流特征，特别是对绕流柱体尾涡区漩涡生成、演化、脱落机制以及柱体间的干扰特性等尚需进行细致的研究.

本文对雷诺数Re=100条件下呈正方形和菱形两种几何布置的四方柱绕流问题进行数值研究.着重探究等边布置四方柱在不同间距比条件下，不同的绕流流场特性、方柱间干扰效应、方柱间流体动力特性，并尝试准确捕捉两种几何阵列情形下柱体绕流的临界间距比.

1 数值方法

1.1 控制方程和参数设定

二维黏性不可压非定常流动的控制方程为连续性方程和不可压Navier-Stokes方程，即

式中：t为时间；vi为速度分量；p为压力；ρ为流体密度；μ为流体动力黏度.

采用有限体积法求解二维黏性不可压非定常Navier-Stokes方程，对流采用二阶迎风格式，压力采用二阶离散格式，压力与速度耦合采用SIMPLEC算法求解.通过对单方柱绕流模型算例的计算，验证了本文算法的有效性.

升力系数、阻力系数、间距比、St数等无量纲数，由以下方程定义，即

式中：Cd为阻力系数，正方向与来流方向相反；CL为升力系数，正方向与来流方向垂直；ρ为流体密度；FD为阻力；U为来流速度；FL为升力；L为方柱中心之间的距离；D为方柱边长；g为间距比；St为斯特劳哈尔数；f为涡脱落频率.

1.2 计算域和边界条件

计算域为长方形，长度D=1，方柱边长为量纲1.四方柱呈正方形布置（布置1）和菱形布置（布置2）两种情况.为了表达方便，对四个方柱分别进行编号为A、B、C、D，具体布置形式及计算区域如图1所示.

相关边界条件，入口边界为速度入口，无量纲速度U=1；出口边界为自由出流；方柱表面为无滑移壁面；上下壁面为滑移壁面.

图1 四方柱布置形式及计算域示意

1.3 网格划分

采用GAMBIT软件对计算域进行非结构三角形网格划分，并对各个四方柱表面进行网格加密，网格划分如图2所示.

图2 柱体表面网格示意

2 结果与讨论

2.1 算例网格无关性及结果验证

首先针对雷诺数为100条件下的单方柱绕流问题进行网格无关性验证.采用网格步长为1进行初步试算并评估试算结果，在流场趋势基本正确的情况下逐步加密网格进行计算，并将多次计算结果进行对比.结果表明，采用网格步长为0.3时阻力系数Cd随网格加密的变化差异在误差范围0.3%以内.

对计算结果进行分析并与经典算例对比，见表1，以验证数学模型与数值模拟方法的准确性.

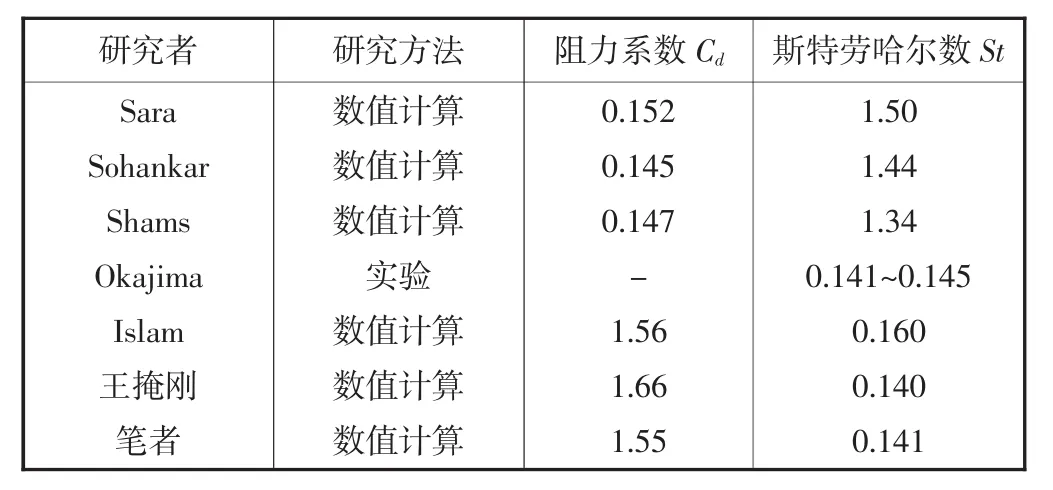
表1 单方柱绕流模拟结果比较

2.2 流动特性

本文对雷诺数为 100，间距比为1.5，2，2.5，3，3.5，4，4.5的两种方柱排列的绕流流场进行了模拟.图3给出了布置1在不同间距比下的涡量.

由图3可见，对于低雷诺数下正方形排列的四方形柱体，随着间距比的逐渐增大，其流场结构呈现出四种特征：①当间距比较小时，四个柱体非常接近，此时流场形态类似于一个大的孤立方柱，在尾流区形成一组涡街，如图3a所示；②当间距比稍微增大时，上流柱体脱落的剪切层附着于下流方柱，在两柱体间出现扭曲的涡场，如图3c所示；③当间距比再继续增大，大于临界间距比时，在上游柱体后发生漩涡的脱落，但漩涡在尚未完全形成时即撞击到下游方柱，如图3d所示；④上游柱体后的漩涡完全脱落，击打在下游柱体上，如图3e所示.

Farrant[10]在模拟四圆柱绕流时认为，漩涡的脱落都是同步的，但从相位上来说，同相脱落和反相脱落都可能出现并会保持一段时间稳定.在本文的四方柱绕流中，漩涡的脱落也符合这个规律.所有稳定的漩涡脱落过程中，漩涡的脱落都是同步的，且同相位和反相位脱落都会发生.

图4给出了布置1在不同间距比下的涡量.

由图4可见，对于低雷诺数下菱形排列的等边四方柱体，随着间距比的逐渐增大，其流场结构呈现出三种特征：①当间距比较小时，四个柱体类似于一个大的孤立方柱，流场特性与单方柱相似，如图4a所示；②当间距比稍微增大时，流体介质从四个柱体中间穿过，由于通道较小而造成狭窄射流，菱形排布的方柱之间产生强烈的相互作用，如图4d所示；③当间距比再继续增大，大于临界间距比时，四个方柱后都产生漩涡脱落，柱B下游形成了成熟的涡脱落连续撞击到柱C上.此间距比下，流场内不同方柱后的涡结构相互干扰，流动特性以及扰动最复杂，如图3e所示.

2.3 阻力和升力系数特性

布置1的各柱阻力系数和升力系数与间距比之间的关系折线如图5所示.

由图5可得以下结论.

（1）上游柱体的阻力系数变化不大，而下游柱体的阻力系数变化较大.当间距比超过临界间距比后，上游柱体后漩涡脱落，并击打到下游柱体上.此时，下游柱体的阻力系数将增大.但随着间距比的进一步增加，阻力系数将会减小，并逐渐趋向于单个柱体绕流时的阻力系数.

（2）方柱A与方柱C的平均升力系数折线关于x=0这条线呈对称分布.方柱B与方柱D的平均升力系数折线关于x=0这条线呈对称分布.

（3）间距比越大，平均升力系数越趋向于零，此时流动状态越趋向于单个柱体的绕流.而间距比较小时，上下两侧柱体的平均升力系数之和接近于零，表明此时上方和下方的两个柱体更像作为一个整体受到升力的作用.

（4）结合绕流流场和升阻力系数变化规律可知，临界间距比在2.5到3之间.

布置2的各柱阻力系数和升力系数与间距比之间的关系折线如图6所示.

由图6可得以下结论.

（1）间距比小于2.5时，四方柱的阻力系数变化都不大，柱C的阻力系数比较小，柱A柱D的阻力系数比较大且升力系数对称分布变化较大.这是因为柱A柱D对称分布阻力特性相同，柱C几乎完全位于其他三根方柱的尾涡之中，类似被屏蔽，阻力较小.

（2）随着间距比的逐渐增大，柱A的阻力系数大幅度减小，柱C的阻力系数大幅度增加.这是因为柱A的自由剪切层逐渐附着到柱C上，一部分阻力也随之作用于柱C上.

（3）当间距比介于3.0到5.0之间时，柱A的阻力系数又大幅度回升，柱C的阻力系数大幅度减小.这是因为此间距比下，流场处于涡冲击模式，每个方柱都受到了来流冲击.

（4）柱A和柱D的平均阻力系数值要比柱B和柱C的大很多.这是因为在菱形排列下，柱A和柱D的上游为均匀来流，其受到的干扰相对较小.

（5）随着间距比的增大，柱A和柱D的平均升力系数一直比较稳定，接近于零.这是因为菱形排布下柱A和柱D上下对称分布，所受升力相互抵消.

（6）结合绕流流场和升阻力系数变化规律可知，临界间距比在3左右.

2.4 涡脱落频率特性

本文计算结果表明，布置1时，上下游柱体的漩涡脱落同步，因此St数相同.这与相关文献的计算结果一致[4，6].而当间距比较小时，四个方柱的涡脱落频率存在微小差异.St数随间距比变化的规律折线如图7所示.

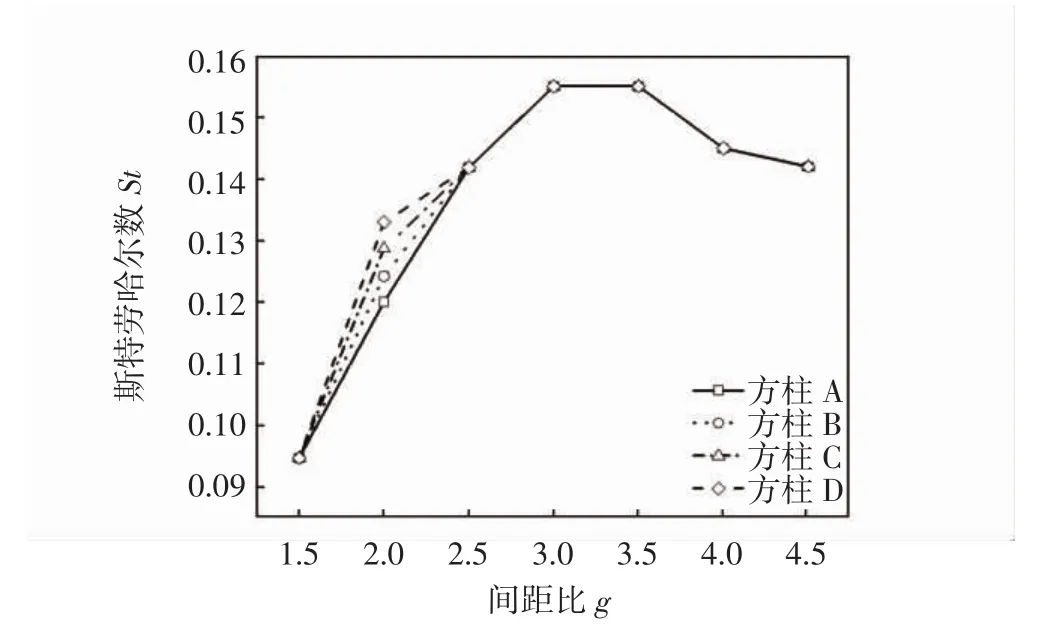
图7 布置1 St随g变化曲线

由图7可以看出：①随着间距比的增加，St先增大后减小，最后接近单方柱绕流的St数；②随着间距比的增大，增加同样间距比时，St数的变化幅度越来越小；③在临界间距比附近，St数的变化幅度较大.

图8为布置2时，St数随间距比变化的规律折线.由图8可以看出：①随着间距比的增加，St先减小后逐渐增大，最后接近单方柱绕流的St数；②在临界间距比之前，四个方柱的漩涡脱落同步，St相同，在临界间距比之后，流场涡脱落频率发生较大变化，四根方柱St出现较大差异，柱A和柱D的St近似，都增加幅度较大后再趋于一稳定值，柱B和柱C的St近似，并平缓趋于一稳定值；③随着间距比的增大，增加同样间距比时，St数的改变幅度越来越小；④在临界间距比附近，St数的改变幅度较大，临界间距比之后漩涡脱落不同步.

图8 布置2 St随g变化曲线

2.5 临界间距比的验证

综上所述，临界间距比是四等边方柱的绕流模拟中极为重要的一个参数，漩涡的脱落，阻力系数，升力系数等参数都在跨过临界间距比时发生改变.现对布置 1，取 g=2.6，2.7，2.8，2.9；布置 2 取 g=2.8，2.9，3.1，3.2进行模拟分析，旨在能够较为准确地捕捉临界间距比的大小.

对于布置1，通过进一步模拟得到在临界间距比附近，平均阻力系数随间距比的变化规律，如图9所示.

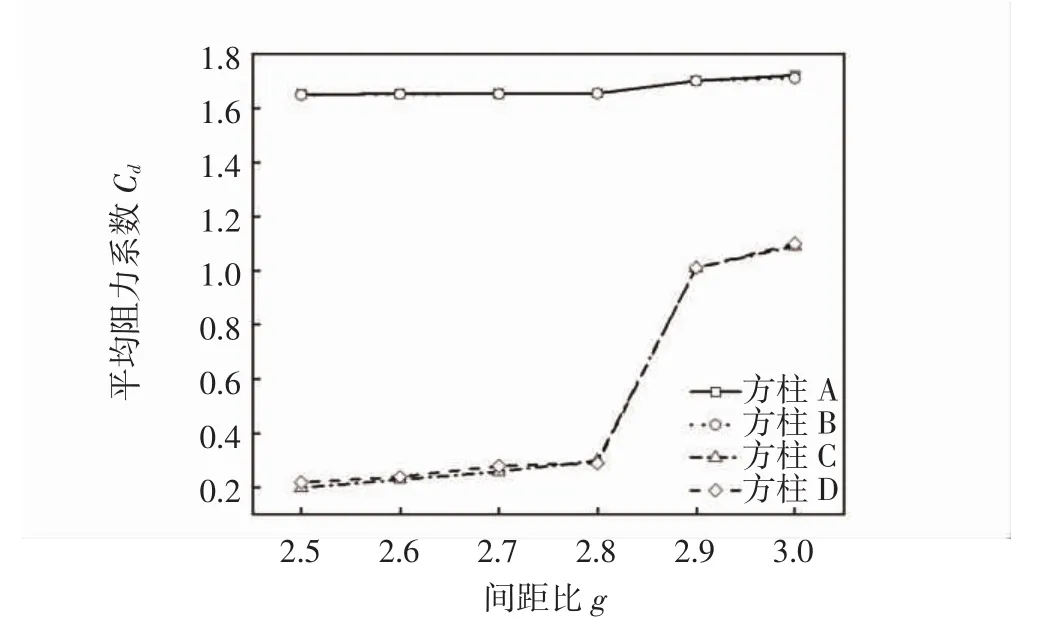
图9 布置1 Cd随g变化曲线

由图9可见，正方形排列四等边方柱绕流的临界间距比为2.8.当间距比超过2.8时，开始在上游柱体后发生漩涡的脱落，上下游柱体的阻力系数都发生跃升.其中，对于下游方柱，超过临界间距比后，阻力系数大约增加了4.1倍.

对于布置2，通过进一步模拟得到在临界间距比附近，平均阻力系数随间距比的变化规律，如图10所示.

由图10可见，菱形排列四等边方柱绕流的临界间距比为3.0.当间距比等于3.0时，流场特性发生较大变化，柱D的阻力系数达到最小值，而柱C的阻力系数达到最大值.其中，对于下游方柱，超过临界间距比后，阻力系数大约增加了1.8倍.

图10 布置2 Cd随间距比g变化曲线

3 结论

本文采用有限体方法，对正方形排列和菱形排列下的四方柱绕流问题进行了数值模拟研究.重点分析了漩涡的脱落规律、升阻力系数随着间距比的变化规律.得出的主要结论如下.

（1）四方柱绕流中也存在着临界间距比现象.并准确地得到了临界间距比的数值.当Re=100时，布置1情形的临界间距比为2.8，布置2情形的临界间距比为3.0.

（2）对于布置1，在临界间距比之前，下游柱体的阻力系数随间距比增加而增加，但幅度较小；当达到临界间距比时，下游柱体的阻力系数出现了陡然的增加.在达到临界间距比后，下游柱体的阻力系数开始逐步减小，最终趋近于单柱体绕流的结果.对于布置2，四个方柱的阻力系数总体变化不大，只是在临界间距比附近出现了大幅度的变化.两种布置下，升力系数折线均关于x=0轴线呈对称分布，并随间距比的变化而逐渐趋向于零.

（3）数值模拟中也观测到了漩涡的同相位和反相位脱落现象，这与实验是相符合的.对于布置1，四方柱漩涡脱落频率相同.对于布置2，四方柱在临界间距比之前漩涡脱落频率相同，在临界间距比之后，漩涡脱落频率出现较大差异.此外，当间距比较小时，流动趋向于不稳定，易于发生相位之间的转换；而当间距比增加到3以上时，相位转换则较少发生.

（4）St数随间距比的增加而增加，且在临界间距比附近时，其增幅最大.

参考文献：

[1]谢志刚，许春晓，崔桂香，等.方柱绕流大涡模拟[J].计算物理，2007，24（2）：171-180.

[2]张爱社，张 陵.等边布置三圆柱绕流的数值分析[J].应用力学学报，2003，20（1）：31-36.

[3]张鹏飞，苏中地，广林端，等.直径变化对三圆柱绕流的影响[J].水动力学研究与进展，2012，27（5）：554-560.

[4]FARRANT T，TAN M，PRICE W G.A cell boundary element method applied to laminar vortex-shedding from arrays of cylinders invarious arrangements[J].Journal of Fluids and Structures，2001，30（2）：211-236.

[5]李景银，CHANK T.绕正方形排列的顺排的四个圆柱的流动研究[J].工程热物理学报，2004，25（1）：59-63.

[6]LAM K，ZOU L.Three-dimensional numerical simulations of cross-flow around four cylinders in an in-line square configuration[J].Journal of Fluids and Structures，2010，26（3）：482-502.

[7]SHAMS U.Numerical simulations of cross-flow around[J].International Journal of Mathematical&Physical and Engineering Sciences，2009，3（2）：76-85.

[8]赵心广.三方柱绕流的大涡模拟及频谱分析[J].水科学与工程技术，2011，28（4）：28-30.

[9]张 伟，戴玉满.低雷诺数下等边布置三方柱绕流的数值研究[D].天津：天津城建大学，2015.

[10]FARRANT T.A cell boundary element method applied to laminar vortex-shedding from arrays of cylinders in various arrangements[J].Journal of Fluids and Structures，2000，14：375-402.