基于子波方差和尺度波长关系的语音识别算法研究

陈理 杨雪梅 毕春艳 陈莹莹

摘  要： 为了提高语音识别的精确度，提出一种将子波方差分析手段应用于基音检测的改进基音检测算法。该算法选用Daubechies子波把信号分解到适当尺度，然后再利用墨西哥帽子波进行子波方差分析;结合子波尺度与波长关系，能够精确地定位基音周期的数值。将其应用于汉语声调的检测中，仿真结果表明，该算法可以根据实际要求调整扫描尺度的精度和范围，具有可调节性。

关键词： 子波方差; 尺度波长; 子波能量; 基音檢测; 声调识别; 语音识别算法

中图分类号： TN912.34?34                  文献标识码： A                          文章编号： 1004?373X（2018）10?0169?03

Abstract： To improve the precision of speech recognition， an improved pitch detection algorithm for applying the wavelet variance analysis means to the pitch detection is proposed. In the algorithm， Daubechies wavelet is selected to an decompose signals to an appropriate scale， and Sombrero wavelet is then used to perform wavelet variance analysis. The numerical value of pitch period can be accurately located based on the relationship between wavelet scale and its wavelength. The algorithm was applied to the detection of Chinese tones. The simulation results show that the algorithm can adjust the precision and range of the scan scale according to actual demands， and has adjustability.

Keywords： wavelet variance; scale wavelength; wavelet energy; pitch detection; tone recognition; speech recognition algorithm

0  引  言

语音信号是非平稳的随机信号，因此对其周期分析和特征提取是比较复杂的问题。在语音学和语音信号处理领域中，将发音时由声带振动而发出的音定义为浊音。浊音是一种近似的周期信号， 其周期称为语音的基音周期[1]。基音周期是语音信号的重要参数，在语音信号处理的许多应用领域里（如语音压缩编码、语音合成、语音识别等），准确可靠地检测语音信号的基音周期都是至关重要的环节，将直接影响到最终结果。

在基音周期分析算法研究这个领域，从20世纪中叶以来出现了很多种基音周期检测方法，其中著名的传统方法有平均幅度差函数法、自相关法等[1]。但由于语音信号本身的复杂性，导致还没有一种能适用于不同说话人和不同噪声环境下的精确基音检测方法。本文将在传统子波基音检测分析方法的基础上，利用语音信号子波系数的子波方差系数精确定位语音的基音周期，并成功应用于汉语语音声调的识别中。

1  基音周期检测的子波方差分析

1.1  子波变换

设[ψ（t）]为一平方可积函数定义为母波， 若其傅里叶变换满足子波函数的容许条件，则将连续子波变换的公式定义为：

比较式（3）和式（4），发现在单一尺度下子波方差和子波能量具有共同的量纲。而子波方差可以视为随机信号在单一尺度下的平均能量。将子波方差随尺度变化的趋势图定义为子波方差变化图如图1所示，该图能反映时间序列中所包含的各种尺度（周期）的波动及其能量强弱随尺度变化的特性[2]。

1.3  基于尺度波长关系的基音周期子波方差分析

由连续子波变换系数决定的子波方差值，反映了信号中所包含的各种尺度（周期）的波动及其强弱随尺度变化的特性。因此可以求出每帧语音信号子波变换系数的各尺度上的子波方差值。其中的最大值对应起主要作用的周期值，即可以精确定位基音周期。

首先，需要选择适当的子波进行子波变换。由于墨西哥帽子波在时域和频域均具有较好的局部性[6?7]，因此选择它进行子波变换。然而，在实际分析中有一个关键问题无法回避，就是求得子波方差最大值的尺度后，如何根据尺度的数值求出实际的周期值。

由图1可知，子波方差能排除各倍频分量的影响，精确地反映基音的基频。当得到Max点对应的尺度J最大值31时，可以根据墨西哥帽子波变换尺度与波长关系式[7]：[λ=（4×π×a）10]，得到实际的波长值（即周期）。以图1为例，先通过a与J的关系求得尺度a=[2（（J+9）/10）]≈16;再求[λ=（4×π×a）10]≈64。于是基音周期[T=λf=648 000]=8 ms，[f]为采样频率。

由于子波变换扫描尺度的精度可以在算法实现中任意调节，因此子波方差法的精确性与复杂度都是可调节的。这需要根据实际需求进行掌控，也是此方法比其他方法优越的地方。更由于其高度的精确性，可以敏感地反映出基频的变化趋势，故适用于汉语语音声调判别等研究。

2  子波分析在语音声调识别中的应用

在汉语语音信号处理和识别领域，声调识别具有至关重要的地位。汉语普通话把声调分成四个声调：一声（阴平）、二声（阳平）、三声（上声）、四声（去声）。不同的声调对应着不同的基音频率变化曲线。

语音声调和基音周期（频率）之间有着明显的联系。说话人的语音基音周期（频率）都是时间序列，汉语言的四个声调对应于不同的基音频率变化趋势。研究出它们之间的联系和变化规律有助于精确地进行语音识别和说话人声音辨识。

为了使基音检测结果更加精确，仍然可以在子波方差分析法之前做信号的预处理。即选用Daubechies子波把信号分解到适当尺度，然后再利用墨西哥帽子波进行子波方差分析。

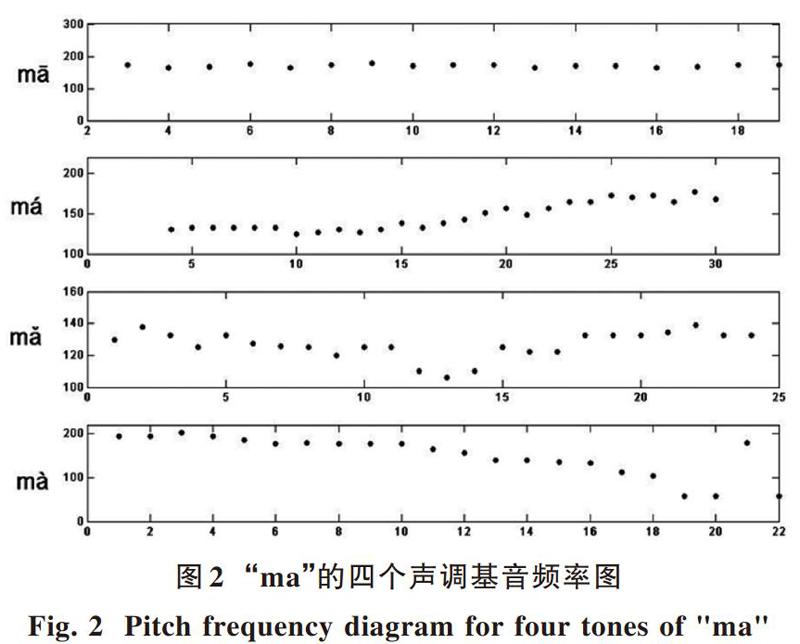
为了验证以上思想，选用汉字“马”的四个声调即“mā，má，mǎ，mà”进行仿真测试，采样频率为8 kHz。由图2“ma”的四个声调基音频率图可以看出：一声的基音频率基本保持不变;二声的基音频率呈逐渐递增的变化;三声是基频先减小，然后递增;而四声则是基频逐渐减少。这些趋势与汉语声调的理论曲线完全一致[8]。

在对连续语音信号进行声调判断时，可遵循以下步骤：首先对原始语音信号进行分帧;其次对每帧信号进行预处理。预处理的方法采用子波变换提取信号基频，也可以为中心消波法;然后对预处理后的语音信号进行周期（频率）细析。本文采用子波方差法：先计算信号的子波系数;然后根据其子波方差值的最大值得出基音周期（频率），求出的基音頻率在人发音频率范围内的视为浊音;最后通过基音频率图判定声调。

图3显示了对连续发音的三字词“早上好”的基频分析。每个字的声调特点都比较明显，“早”和“好”字是三声，因此基频先下降后递增，“上”字是四声，基频趋势一直下降。

3  结  语

本文采用的子波方差分析方法，可以根据实际要求调整扫描尺度的精度和范围，具有可调节性。同时充分发挥了子波变换多分辨率优势，利用尺度与波长关系，精确地定位基音周期（频率）的数值，因此又具有精确性。和传统的基音检测算法，如自相关法、平均幅度差法相比，由于该分析模型追求了高的精度，因此计算量稍大，实时性较弱。但是该模型对语音信号频率微弱变化的敏感性，使其非常适合进行汉语声调检测等要求准确性较高的分析工作。

参考文献

[1] 赵力.语音信号处理[M].北京：机械工业出版社，2003.

ZHAO Li. Voice signal processing [M]. Beijing： China Machine Press， 2003.

[2] 陈理，袁晓，汤韩杰，等.金融时间序列结构波动的子波变换分析[J].四川大学学报（自然科学版），2007，44（2）：293?298.

CHEN Li， YUAN Xiao， TANG Hanjie， et al. Structural wave analysis of financial time series by wavelet transform [J]. Journal of Sichuan University （Natural science edition）， 2007， 44（2）： 293?298.

[3] 陈理，田巧玉.基于子波变换的时间序列波动特征分析[J].技术与市场，2009，16（7）：49?50.

CHEN Li， TIAN Qiaoyu. Structural wave analysis of financial time series by wavelet transform [J]. Technology and market， 2009， 16（7）： 49?50.

[4] 杨艺，李建勋，柯熙政.小波方差在信号特征提取中的应用[J].传感器世界，2006，12（1）：33?35.

YANG Yi， LI Jianxun， KE Xizheng. Study on wavelet variance and its application in signal feature extraction [J]. Sensor world， 2006， 12（1）： 33?35.

[5] Stephane Mallat.信号处理的小波导引[M].北京：机械工业出版社，2002.

MALLAT S. A wavelet tour of signal processing [M]. Beijing： China Machine Press， 2002.

[6] 崔锦泰.小波分析导论[M].西安：西安交通大学出版社，1995.

CUI Jingtai. An introduction to wavelets [M]. Xian： Xian Jiaotong University Press， 1995.

[7] Ingrid Daubechies.小波十讲[M].北京：国防工业出版社，2004.

DAUBECHIES I. Ten lectures on wavelets [M]. Beijing： National Defense Industry Press， 2004.

[8] 汤韩杰，袁晓.子波分析中尺度与波长的关系[J].电子科技大学学报，2006，35（1）：13?16.

TANG Hanjie， YUAN Xiao. Relationship between scale and wavelength in wavelet transform analysis [J]. Journal of University of Electronic Science and Technology of China， 2006， 35（1）： 13?16.

[9] 黄昌宁，夏莹.语言信息处理专论[M].北京：清华大学出版社，1996.

HUANG Changning， XIA Ying. The language information processing [M]. Beijing： Tsinghua University Press， 1996.

[10] 张梅.一种语音端点检测算法及其在DSP上的实现[J].电子技术应用，2012，38（8）：133?134.

ZHANG Mei. An algorithm for speech endpoint detection and its implementation on DSP [J]. Application of electronic technique， 2012， 38（8）： 133?134.

[11] 陈理，徐晋，冯子芥，等.一种基于移动终端的智能水杯垫设计及应用[J].现代电子技术，2017，40（18）：83?84.

CHEN Li， XU Jin， FENG Zijie， et al. Design and application of a smart cup pad based on mobile terminal [J]. Modern electronics technique， 2017， 40（18）： 83?84.