振铃波作用下低压配电系统SPD防护失效概率分析
2018-05-15徐敦彬袁光伟高海龙王永力
徐敦彬,袁光伟,郝 威,高海龙,王永力
(国网江苏省电力公司徐州供电公司,江苏徐州 221005)
0 引言
雷电过电压是电力系统运行面临的主要威胁之一[1],氧化锌压敏电阻因其优异的限压特性成为应用最为广泛的电涌保护器件[2]。目前针对压敏电阻防护研究,一般采用8/20 μs、10/350 μs等脉冲电流波形或8/20-1.2/50 μs组合波波形[3-4],具体配合机理、搭配方式、保护距离等相关研究较为成熟[5-6]。但是实际线路雷电过电压观测数据[7]表明:雷击过电压一般呈衰减振荡波形,首个脉冲波头时间非常短。采用单次脉冲源或组合波波形对低压配电系统压敏电阻防护分析可能与真实雷电过电压作用存在较大差异,尤其是在热量、电荷累积方面[8]。因此,IEEE相关标准[9]中也推荐采用0.5 μs-100 kHz振铃波模拟真实雷电过电压。需要研究振铃波作用下低压配电系统,尤其是具体配电制式中电涌保护器的防护效果。
本文利用 EMTP[10]搭建 0.5 μs-100 kHz振铃波发生回路,采用P-G氧化锌压敏电阻等效模型,分析TN-C-S配电系统下压敏电阻防护效果,通过累积能量计算压敏电阻失效概率,并讨论冲击电压幅值和接地电阻对压敏电阻失效概率的影响。
1 振铃波发生电路模型
根据IEEE给出的0.5 μs-100 kHz振铃波定义[9],第1个波头时间为0.5 μs,振荡频率为100 kHz,在3~6个周期内幅值衰减至初始峰值的60%以下。图1给出了振铃波发生电路图。振铃波发生电路主要由5个部分组成:高压贮能电路、振荡电路、时间常数匹配电路、输出阻抗匹配电路和高压开关电路[11]。

图1 振铃波发生器电路Fig.1 Circuit of the ring wave generator
根据IEEE C62.41—1991给出的位置类别,振铃波试验的电压等级见表1[11]。
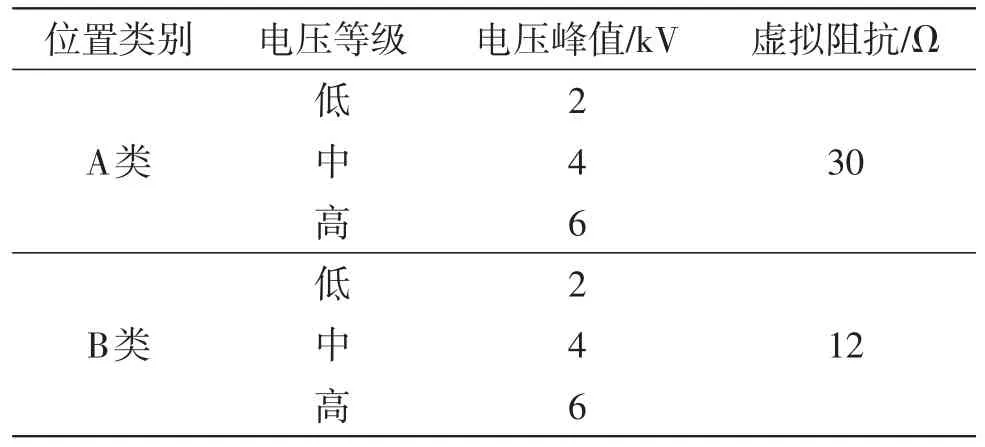
表1 振铃波试验的电压等级Table 1 Experimental voltage level of the ring wave
A类位置表示长支线电路及引出线,B类位置表示馈线、短支线电路及负载中心。图2给出了A类振铃波波形,电压幅值为6 kV。
2 低压配电线路冲击模型
图3给出了TN-C-S配电系统采用压敏电阻防护分析模型[12]。仿真过程中,在L线与N线间施加冲击电压,在L线与N线、N线与PE线间安装SPD。

图2 0.5 μs-100 kHz振铃波Fig.2 0.5 μs-100 kHz ring wave
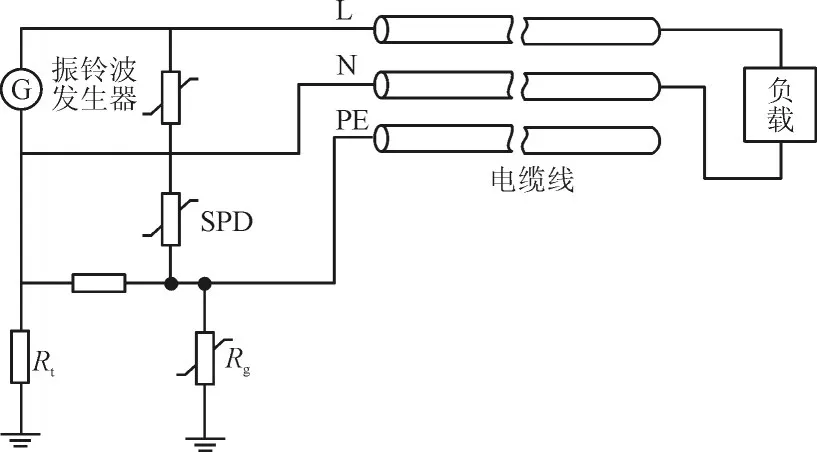
图3 TN-C-S配电系统分析模型Fig.3 Analysis model of TN-C-S distribution system
压敏电阻与负载之间采用电缆连接,电缆型号为单芯聚氯乙烯(PVC)绝缘电缆,电缆电气参数通过下式计算[13]:

式中:a为电缆芯线半径;l为电缆长度,ρ为电缆电阻率。电缆线长度10 m,电缆标称截面2 mm2,电阻率1.72×10-8Ω·m,相对介电常数4.5,相对磁导率1。
目前较为常用的压敏电阻电路模型主要有非线性电阻模型、非线性电感模型、IEEE模型[14]和PG模型[15]。相关实验与仿真数据[16]表明,P-G模型具有较高的精度且电路模型较为简单,因此仿真中采用P-G压敏电阻电路模型,压敏电阻标称放电电压为470 V。
3 仿真分析
3.1 SPD残压与通流
图4给出了振铃波作用下L-N线间、N-PE线间压敏电阻残压和电流。振铃波波形分别采用A类6 kV和B类6 kV,接地电阻Rg取4 Ω。

图4 SPD残压与电流Fig.4 SPD residual voltages and currents
由图4可看出,无论是A类波形还是B类波形,振铃波作用下L-N线间、N-PE线间电压均得到较好的抑制,负载设备及其绝缘均不会遭受过电压威胁。虽然N-PE线间SPD残压远低于L-N线间SPD残压,但仍存在一定电位差,会产生电压漂移。SPD间通流相差较大,L-N线间SPD最大通流远大于N-PE线间SPD。由于B类波形的虚拟阻抗较小,B类波形作用下,SPD的残压与通流均高于A类。
3.2 冲击电压幅值影响
表2给出了L-N线间SPD残压与通流随冲击电压幅值变化情况,接地电阻4 Ω。

表2 SPD残压随冲击电压幅值变化Table 2 Residual voltages vs impulse voltage amplitudes
由表2可看出,L-N线间SPD的残压和通流随着冲击电压幅值的增大而增加,但是B类波形作用下,残压增加幅度相对较小。B类波形下,SPD的残压和通流均高于A类,因此对SPD防护的威胁也更大。
3.3 SPD接地电阻影响
图5给出了L-N线间残压随接地电阻变化情况,冲击电压幅值6 kV。

图5 SPD残压随接地电阻变化Fig.5 SPD residual voltages vs grounding resistance
由图5可看出,无论是A类还是B类波形,L-N线间SPD的残压随着接地电阻的增加而增大50 Ω接地电阻情况下,B类波形冲击后SPD残压为1209V,超过了I类电压保护水平1.2 kV[17],不能为负载设备提供有效过电压防护。
3.4 失效概率
由于振铃波冲击持续时间为μs量级,大量能量迅速注入压敏电阻,局部热量不能及时向外传递,因此冲击作用可以看作绝热升温过程。大量热量积累导致压敏电阻内部晶粒热导率的下降,部分热导性能较差的晶界由热平衡状态转入热不平衡状态,晶界区电荷量产生变化,最终可能引起压敏电阻破裂破坏。
通过比较压敏电阻吸收能量Es是否超过其能量阈值ER来判断压敏电阻是否失效。计算中压敏电阻能量阈值取3 840 J[18]。压敏电阻吸收的能量Es计算如下:
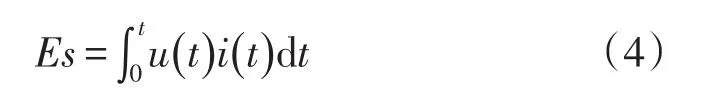
式中,u(t)和i(t)分别为流经压敏电阻的电压和电流。
压敏电阻超过其能量阈值后的累积失效概率函数服从威布尔分布[18]:

由于N-PE线间SPD承受的残压和通流幅值较小,主要考虑L-N线间SPD的失效概率。图6给出了L-N线间SPD失效概率随冲击电压幅值变化情况,接地电阻4 Ω。
从图6可以看出,L-N线间SPD失效概率随着冲击电压幅值的增加而增大。B类波形作用下,SPD失效概率的变化尤为明显。当冲击电压达10 kV时,B类波形作用下,SPD失效概率超过了10%。残压持续时间过长和热量来不及向外泄散是导致较高失效概率的原因。
图7给出了L-N线间SPD失效概率随接地电阻变化情况,冲击电压幅值6 kV。
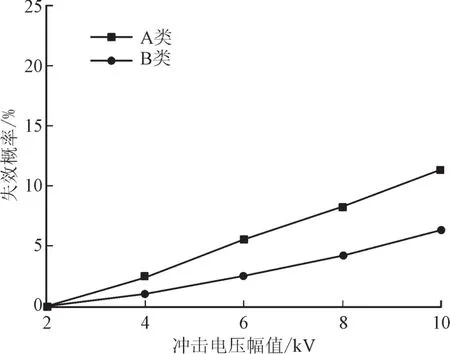
图6 失效概率随冲击电压幅值变化Fig.6 Failure probability vs impulse voltage amplitudes

图7 失效概率随接地电阻变化Fig.7 Failure probability vs grounding resistance
从图7可以看出,L-N线间SPD失效概率随着接地电阻的增加而增大。B类波形作用下,SPD失效概率明显高于A类,且这种趋势随着接地电阻增大愈发明显。这主要是由于B类波形作用导致的SPD通流受接地电阻影响较大。因此,为了确保SPD的防护效果,需要尽可能降低SPD的接地电阻。
4 结论
利用EMTP软件搭建0.5 μs-100 kHz振铃波发生电路,模拟真实雷电过电压,对低压配电系统SPD防护效果进行分析,得到结论如下:
1)TN-C-S配电系统中,在L线与N线、N线与PE线间安装SPD时,振铃波冲击下电路残压能够得到较好的抑制,且L-N线间SPD残压和通流远大于N-PE线间SPD。
2)L-N线间SPD的残压随着冲击电压幅值、接地电阻的增大而增加,B类波形作用下,SPD的残压与通流均高于A类。
3)L-N线间SPD失效概率均随着冲击电压幅值和接地电阻的增加而增大,B类波形作用下,SPD失效概率要高于A类。
参考文献:
[1]吴广宁,曹晓斌,李瑞芳.过电压防护的理论与技术[M].北京:中国电力出版社,2015.
[2]李祥超.电涌保护器(SPD)原理与应用[M].北京:气象出版社,2011.
[3]杜志航,杨仲江,姜山,等.基于限压型电涌保护器能量配合的分析[J].电瓷避雷器,2009(5):46-49.DU Zhihang,YANG Zhongjiang,JIANG Shan,et al.Analyse on energy coordination between based on voltage limiting SPD[J].Insulators and Surge Arresters,2009(5):46-49.
[4]姜辉,刘全桢,刘宝全,等.低压配电系统电涌保护器能量配合研究[J].电瓷避雷器,2013(3):137-142.JIANG Hui,LIU Quanzhen,LIU Baoquan,et al.Re⁃search on energy coordination of SPD in low-voltage distri⁃bution system[J].Insulators and Surge Arresters,2013(3):137-142.
[5]LI M,YUAN J,ZHAO Z.Low-voltage SPD coordination analysis[C].2011 Asia-Pacific International Conference on Lightning.Chengdu,2011:913-916.
[6]段振中,柴健,朱传林.限压型低压电涌保护器级间能量配合方式的仿真研究[J].电瓷避雷器,2013(1):102-106.DUAN Zhenzhong,CHAI Jian,ZHU Chuanlin.Simula⁃tion research on energy cooperation mode between levels of Voltage-Limiting low voltage SPD[J].Insulators and Surge Arresters,2013(1):102-106.
[7]蔡力,王建国,周蜜,等.一次近距离自然闪电输电线路感应电压观测[J].高电压技术,2013,39(4):1000-1008.CAI Li,WANG Jianguo,ZHOU Mi,et al.Observation of induced voltage on power lines under a nearby natural lightning[J].High Voltage Engineering,2013,39(4):1000-1008.
[8]SHIN H K,KIM D S,CHUNG Y K,et al.Energy coordina⁃tion of ZnO varistor based SPDs in surge current due to di⁃rect lightning flashes[C]
[9]Surge arresters Part 2:Metal-oxide surge arresters without gaps for AC system:IEC Standard 60099-4[S].2001.
[10]吴文辉,曹祥麟.电力系统电磁暂态计算与EMTP应用[M].北京:中国水利水电出版社,2012.
[11]余志勇,刘光斌.振铃波抗扰度试验的发展及应用分析[C]第十五届全国电磁兼容学术会议论文集.广州,2005.
[12]何金良,曾嵘.配电线路雷电防护[M].北京:清华大学出版社,2013.
[13]ŠkuletiS,RaduloviV.Analysis of surge protection per⁃formance in low-voltage AC systems with capacitive load[C].Universities Power Engineering Conference.IEEE,2010:1-6.
[14]IEEE working group 3.4.11.Modeling of metal oxide surge arresters[J].IEEE Transactions on Power Delivery,1995,10(2):393-397.
[15]PINCETI P,GIANNETTONI M.A simplified model for Zinc oxide surge arresters[J].IEEE Transactions on Power Delivery,1999,14(2):393-398.
[16]王荣珠,张云峰,陈则煌,等.基于ATP-EMTP仿真软件的MOV仿真模型的分析[J].电瓷避雷器,2014(5):66-70.WANG Rongzhu,ZHANG Yunfeng,CHEN Zehuang,et al.Analysis of MOV simulation model based on ATP-EMTP[J].Insulators and Surge Arresters,2014(5):66-70.
[17]Surge protective devices connected to low-voltage power distribution systems-selection and applications principles:IEEE 61643-12[S].2011.
[18]SHARIATINASAB R,AJRI F,DAMAN-KHORSHID H.Probabilistic evaluation of failure risk of transmission line surge arresters caused by lightning flash[J].IET Genera⁃tion Transmission&Distribution,2014(8):193-202.
