高考分布列研究
2018-05-14沈怡欣
沈怡欣
一、专题考点分析
综观2012-2016年高考数学试题,分布列部分考查的知识点覆盖面广,新课标理科试卷共有 6份,分别是2016新课标全国Ⅰ卷、全国Ⅱ卷、全国III;2013新课标全国Ⅰ卷、全国Ⅱ卷;2012新课标全国卷
二、题型难度分析
针对分布列的考查,所有试题均以考查学生基础知识、基本能力为主线,
三、知识点考试频率统计分析
高考在分布列这个考点上主要考察超几何分布,二项分布,离散型随机变量及其分布列。从近四年的高考试题来看,2012年新课标理科1卷填空题第15题、解答题第18题,考查正态分布、离散型随机变量及其分布列、期望、方差;2013年新课标理科2卷解答题第19题,考查离散型随机变量及其分布列和期望;2014年新课标理科2卷解答题第18题,考查正态分布、二项分布、期望;2015年新课标理科1卷解答题第19题,考查正态分布及二项分布。
四、考题具体分析
1.(2016年全国I高考)某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记 表示2台机器三年内共需更换的易损零件数, 表示购买2台机器的同时购买的易损零件数.
(I)求 的分布列;
(II)若要求 ,确定 的最小值;
(III)以購买易损零件所需费用的期望值为决策依据,在 与 之中选其一,应选用哪个?
2.(2016年全国II高考)某险种的基本保费为 (单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下: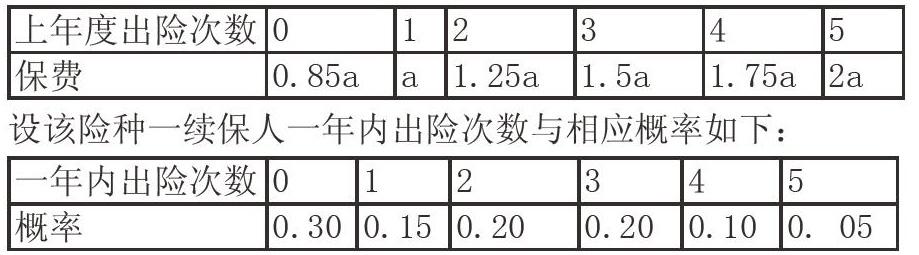
(Ⅰ)求一续保人本年度的保费高于基本保费的概率;
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.
3.(2013年高考新课标1(理))一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.
4.(2012年高考新课标(理))某花店每天以每枝 元的价格从农场购进若干枝玫瑰花,然后以每枝 元的 价格出售,
如果当天卖不完,剩下的玫瑰花作垃圾处理。
(1)若花店一天购进 枝玫瑰花,求当天的利润 (单位:元)关于当天需求量
(单位:枝, )的函数解析式。
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
以100天记录的各需求量的频率作为各需求量发生的概率。
(i)若花店一天购进 枝玫瑰花, 表示当天的利润(单位:元),求 的分布列,
数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?
请说明理由。
五、命题趋势
高中学习的“概率统计”是大学统计学的基础,起着承上启下的作用,是每年高考命题的热点. 从近几年的试题可展望2017 年的高考,其命题趋势应该具有如下特点.
① 重考查应用意识和创新能力.
② 高考对概率与统计内容的考查,往往以实际应用题出现,这既是这类问题的特点,也符合高考发展的方向. 概率、统计解答题,侧重于分布列与期望. 近几年的高考有以概率应用题替代传统应用题的趋势;2017 年高考将继续秉承考试中心提出的“突出应用能力考查”以及“突出新增加教学价值和应用功 能”的指导思想,离散型随机变量分布列及相关问题的考查是主流,统计案例等也会经常出现.在大题的考查中,多以分布列为载体进行考查,但会融入相关知识,因此,备考要注重知识点的覆盖,不能留下漏洞.
③ 注重学科内知识间的交会.
鉴于培养学生数学核心素养的目标,今后概率统计与计数原理更多会关注知识间的迁移,主动建模意识仍是解决问题的关键. 概率是与各章知识交会的学习
六、教学建议
1. 分布列部分一定要认真落实基础知识,掌握基本的计算能力,逻辑思维能力
2.注意列表时把所有可能取到的所有值都列出,然后分别算概率
3.最后注意检查所有概率和是否是1。
