永磁同步电机闭环控制系统数字PI参数整定

刘景林 公超 韩泽秀 王晓梅

摘 要：为了研究简单、准确的永磁同步电动机数字PI控制器参数整定方法；改进了常用的在连续域内整定PI参数的过程，采用了在w′域内进行参数设计的离散化方法，将采样时间和零阶保持器（ZOH）引起的相角滞后直接体现在设计过程中，具体研究内容为：首先建立系统各环节的数学模型，并得到闭环系统的离散模型框图；接着利用工程经验将时域性能指标转换成开环频域特征量，并在w′域内解析计算得到了PI控制器参数。整定过程采用先电流内环后转速外环的方式，仿真和实验发现利用该设计方法得到的结果满足设计要求，超调量小于5%，调节时间约1.92 s，研究表明该方法可以为永磁同步电动机数字PI控制器参数整定提供指导。

关键词：永磁同步电动机；PI控制器参数；离散化；电流环；转速环

中图分类号：TM 351

文献标志码：A

文章编号：1007-449X（2018）04-0026-07

Abstract：In order to obtain a simple and accurate design method of digital PI controller parameter for permanent magnet synchronous motor， the method of tuning PI parameters in continuous domain is improved.A discrete design method of tuning parameter in the w′ domain was employed. The phase lag caused by the sampling time and the zero-order holder （ZOH） were directly reflected in the design process.The mathematical model of every link of the system was determined and the discrete model block diagram of the closed loop system was got in the first place. And then， the time domain performance index was transformed into the open-loop frequency domain feature value by engineering experience， which was followed by the analysis in the w′ domain. In this paper， the tuning process contained current loop analysis prior to speed loop. The simulation and experiment show that the results obtained by the proposed method meet the performance requirements， with an overshoot of less than 5% and settling time of about 1.92 s， which proves that this method can provide the guidance for parameter tuning of digital PI controller.

Keywords：permanent magnet synchronous motor （PMSM）； PI controller parameter； discretization； current loop； speed loop

0 引 言

永磁同步电动机（permanent magnet synchronous motor，PMSM）具有功率因数大、效率高、功率密度大和调速范围宽等优点，已经在电梯、伺服系统和电动汽车等工业领域得到了广泛的应用[1]；与此同时，永磁同步电动机控制技术也在不断改进与完善[2]。基于数字PI控制器的双闭环矢量控制系统易于实现且控制效果好，在工程中已被广泛采用[3]。

目前，将PMSM双闭环控制系统看作线性连续系统，在连续域内进行PI参数整定的技术已经趋于成熟，其中，文献[4]根据经典控制理论，将电动机控制系统进行简化，得出PI参数解析计算公式；文献[5]采用数值分析计算的方法，以优化系统的抗负载干扰能力为目标进行PI参数整定，经过复杂的数学推理之后得到了比较简单的参数计算公式；文献[6]研究了基于主導极点和相位裕度的PID参数整定方法，依据主导极点的配置原理得到PID整定式；文献[7]与[8]建立了较为精确的PMSM双闭环控制系统模型，根据设定的期望截止频率和相位裕度，在s域内完成了PI参数设计工作。

虽然在s域内进行系统分析的方法比较简单，但需要将PI控制器看作连续模块，然而，常用的PI控制器是在数字处理器内编程实现的数字模块，所以，在离散域内分析PMSM双闭环控制系统能够取得更好的结果，主要原因包括：1）数字PI控制器参数与控制系统的采样周期具有紧密关系[9]，而在连续域内整定PI参数的方法并不能将其体现出来；2）只有当采样频率相对于系统工作频率足够高时，零阶保持器（zero-order holder，ZOH）引起的附加相角滞后才可忽略[10]，而高速电机的工作频率与采样频率差别并不大，特别是电流环。文献[11]指出离散域设计方法能够避免离散化误差，可在选定的采样周期下保证系统性能达到指标要求，但在离散域内设计PMSM双闭环系统PI控制器参数的工作并不常见。本文首先建立了包含ZOH的PMSM双闭环控制系统离散模型；接着，直接利用工程经验将时域性能指标转换成开环频域特征量，简化了设计过程并在w′域内采用频率分析法完成了PI参数整定；最后，仿真和实验验证了本文设计方法的有效性。

1 双闭环控制系统模型

1.1 PMSM模型

在忽略铁心磁饱和且不计涡流和磁损耗的前提下，PMSM在dq同步旋转坐标系下的电压方程为

在采用状态反馈补偿法实现电机的模型解耦后[12]， 对式（1）～式（3）进行拉普拉斯变换得到s域内电机模型如图1所示。

1.2 逆变器模型

电压逆变器基本模型可以等效为一阶惯性环节：

1.5 控制系统的离散模型

依据离散系统模型建立方法[13]配置采样器和ZOH的位置，图2是包含ZOH的PMSM双闭环控制系统的离散模型框图。

2 数字PI控制器参数整定

2.1 高阶系统开环频域特征量与时域指标间关系

在频域内分析、设计系统，常以开环频域特征量（相角裕度γ、幅值裕度h、开环增益K和剪切频率ωc）作为依据，然而项目中给出的一般是闭环系统的时域指标，即调节时间ts（单位阶跃响应保持与终值±2%误差的时间）、超调量σ%和稳态误差ess，因此，得到频域特征量与时域指标之间的关系可以为频域设计明确方向。对高于三阶的系统，准确推导出ωc、γ与ts、σ%的关系不但非常困难且不具有实用价值，在控制工程中，一般采用在工程实践中总结出来的经验来描述时域指标与频域特征量之间的关系[13]，如图3和图4所示，由图可知，γ越大，σ%越小，且当γ一定时，ts随着ωc增大而减小；h与时域指标之间没有确定关系，但一般要求h≥10 dB，可作为约束条件判断所设计参数的合理性。工程上，希望相角裕度取值范围在30°到70°之间。

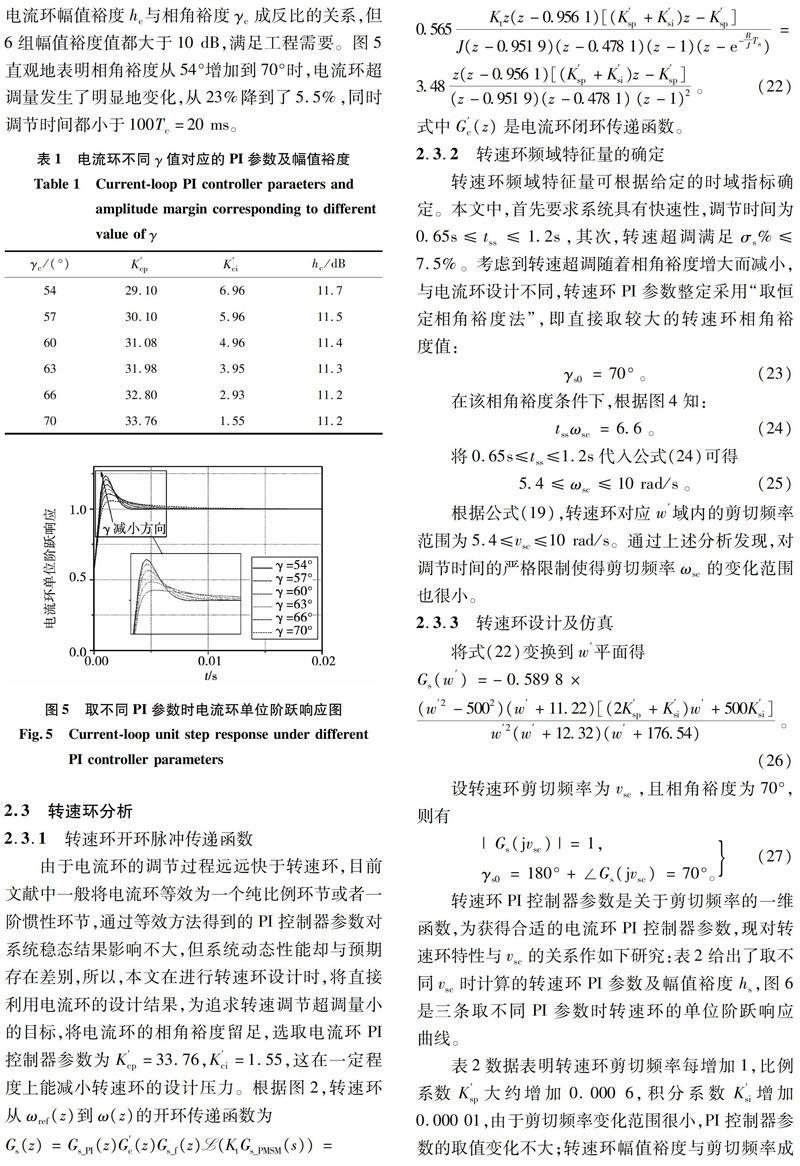
表1数据表明电流环相角裕度值每增加3°，比例系数K′cp大约增加1，而积分系数K′ci降低1；另外，电流环幅值裕度hc与相角裕度γc成反比的关系，但6组幅值裕度值都大于10 dB，满足工程需要。图5直观地表明相角裕度从54°增加到70°时，电流环超调量发生了明显地变化，从23%降到了5.5%，同时调节时间都小于100Tc=20 ms。

2.3 转速环分析

2.3.1 转速环开环脉冲传递函数

由于电流环的调节过程远远快于转速环，目前文献中一般将电流环等效为一个纯比例环节或者一阶惯性环节，通过等效方法得到的PI控制器参数对系统稳态结果影响不大，但系统动态性能却与预期存在差别，所以，本文在进行转速环设计时，将直接利用电流环的设计结果，为追求转速调节超调量小的目标，将电流环的相角裕度留足，选取电流環PI控制器参数为K′cp=33.76，K′ci=1.55，这在一定程度上能减小转速环的设计压力。根据图2，转速环从ωref（z）到ω（z）的开环传递函数为

2.3.2 转速环频域特征量的确定

转速环频域特征量可根据给定的时域指标确定。本文中，首先要求系统具有快速性，调节时间为0.65s≤tss≤1.2s，其次，转速超调满足σs%≤7.5%。考虑到转速超调随着相角裕度增大而减小，与电流环设计不同，转速环PI参数整定采用“取恒定相角裕度法”，即直接取较大的转速环相角裕度值：

根据公式（19），转速环对应w′域内的剪切频率范围为5.4≤vsc≤10 rad/s。通过上述分析发现，对调节时间的严格限制使得剪切频率ωsc的变化范围也很小。

2.3.3 转速环设计及仿真

将式（22）变换到w′平面得

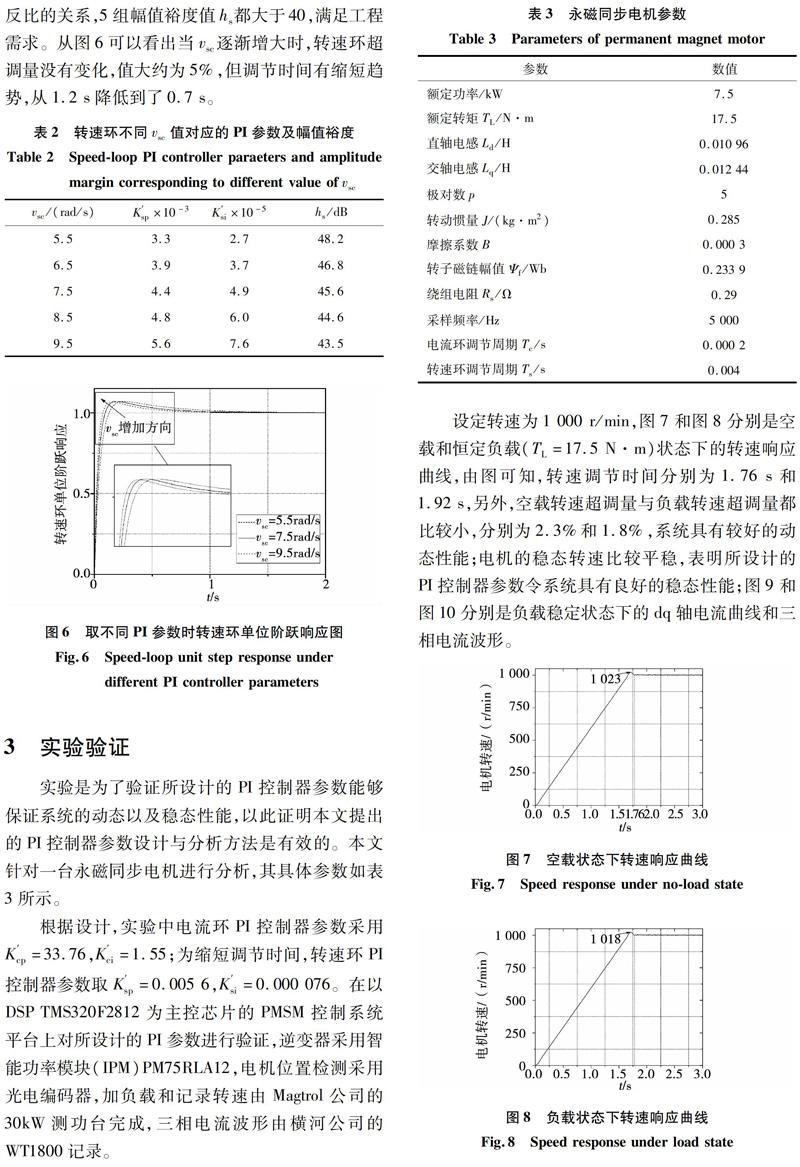
转速环PI控制器参数是关于剪切频率的一维函数，为获得合适的电流环PI控制器参数，现对转速环特性与vsc的关系作如下研究：表2给出了取不同vsc时计算的转速环PI参数及幅值裕度hs，图6是三条取不同PI参数时转速环的单位阶跃响应曲线。

表2数据表明转速环剪切频率每增加1，比例系数K′sp大约增加0.000 6，积分系数K′si增加0.000 01，由于剪切频率变化范围很小，PI控制器参数的取值变化不大；转速环幅值裕度与剪切频率成反比的关系，5组幅值裕度值hs都大于40，满足工程需求。从图6可以看出当vsc逐渐增大时，转速环超调量没有变化，值大约为5%，但调节时间有缩短趋势，从1.2 s降低到了0.7 s。

3 实验验证

实验是为了验证所设计的PI控制器参数能够保证系统的动态以及稳态性能，以此证明本文提出的PI控制器参数设计与分析方法是有效的。本文针对一台永磁同步电机进行分析，其具体参数如表3所示。

根据设计，实验中电流环PI控制器参数采用K′cp=33.76，K′ci=1.55；为缩短调节时间，转速环PI控制器参数取K′sp=0.005 6，K′si=0.000 076。在以DSP TMS320F2812为主控芯片的PMSM控制系统平台上对所设计的PI参数进行验证，逆变器采用智能功率模块（IPM）PM75RLA12，电机位置检测采用光电编码器，加负载和记录转速由Magtrol公司的30kW测功台完成，三相电流波形由横河公司的WT1800记录。

设定转速为1 000 r/min，图7和图8分别是空载和恒定负载（TL=17.5 N·m）状态下的转速响应曲线，由图可知，转速调节时间分别为1.76 s和1.92 s，另外，空载转速超调量与负载转速超调量都比较小，分别为2.3%和1.8%，系统具有较好的动态性能；电机的稳态转速比较平稳，表明所设计的PI控制器参数令系统具有良好的稳态性能；图9和图10分别是负载稳定状态下的dq轴电流曲线和三相电流波形。

4 结 论

本文在w′域内采用频率法设计了PMSM转速环与电流环的PI控制器参数，离散化设计方法将采样频率对参数的影响以及ZOH引起的相角滞后考虑在内，所设计的参数更加准确；为在w′域内进行分析，直接利用工程经验公式将时域指标转换成开环频域特征量，这降低了系统设计的复杂性。仿真与实验结果表明，采用频率法校正的系统具有良好的稳态与动态性能，满足工程需要。

参 考 文 献：

[1] 王斌，王跃，王兆安. 空间矢量调制的永磁同步电机直接转矩控制[J]. 电机与控制学报，2010，（06）：45.

WANG Bin， WANG Yue， WANG Zhaoan. Direct torque control of permanent magnet synchronous motor drives using space vector modulation[J]. Electric Machines and Control， 2010，（06）：45.

[2] 鮑禄山，王毅非，黎燕. 基于矢量解耦与预测电流控制相结合的APF的研究[J]. 电力系统保护与控制，2015，05：88.

BAO Lushan， WANG Yifei， LI Yan. Research on APF based on vector decoupling control and predictive current control [J]. Power System Protection and Control， 2015，05：88.

[3] 周明磊，游小杰，王琛琛.电力机车牵引传动系统矢量控制[J]. 电工技术学报， 2011，09：110.

ZHOU Minglei， YOU Xiaojie， WANG Chenchen.Vector control of driving system of locomotive[J]. Transactions of China Electrotechnical Society， 2011，09：110.

[4] 董恒，王辉，黄科元. 永磁同步电动机驱动系统数字PI调节器参数设计[J]. 电气传动，2009，01：7.

DONG Heng， WANG Hui， HUANG Keyuan. Design of PMSM drive system digital PI adjuster parameters [J]. Electric Drive，2009，01：7.

[5] H PANAGOPOULOS， K J ASTROM， T HAGGLUND. A numerical method for design of PI controllers[C]//IEEE International Conference on Control Applications in Hartford， CT， USA， 1997.USA：IEEE，1997.

[6] TANG E W，HUANG J，WU J，et al.A PID tuning method based on dominant poles and phase margin[C]//Proceedings of the 29th Chinese Control Conference in Beijing， 2010.USA： IEEE， 2000.

[7] 王莉娜，朱鸿悦，杨宗军. 永磁同步电动机调速系统PI控制器参数整定方法[J]. 电工技术学报，2014，05：104-117.

WANG Lina， ZHU Hongjun， YANG Zongjun. Tuning mehod for PI controllers of PMSM driving system[J]. Transactions of China Electrotechnical Society. 2014，05：104-117.

[8] LIDOZZI A，SOLERO L，CRESCIMBINI F et al.Direct tuning strategy for speed controlled PMSM drives[J]. IEEE International Symposium on Industrial Electronics， 2010， pp. 1265.

[9] BOGUS E G，HOSKINS M J，B J HUNSINGER.Sampling time effects in the ACT device[J]. IEEE Transactions on Ultrasonics， Ferroelectrics， and Frequency Control， 1991， pp. 344.

[10] Principles and Pratices of Automatic Process Control [D]. USA： John Wiley & Sons， 2008.

[11] Karl J.Astrom， Bjorn Wittenmark. Computer control system—theory and design[M]. 北京： 清华大学出版社， 2002.

[12] SINHA P.State feedback decoupling of nonlinear systems[J]. IEEE Transactions on Automatic Control， 1977：487.

[13] 卢京潮.自动控制原理[M].西安：西北工业大学出版社，2009：220-224.

（编辑：刘素菊）