二自由度飞行姿态模拟器自整定控制器设计
2018-05-14尹航杨烨峰赵岩梁悦班晓军
尹航 杨烨峰 赵岩 梁 悦 班晓军

摘 要:以一套可变负载的二自由度飞行姿态模拟器为实验平台,研究变负载下的飞行器的自适应控制问题。根据继电反馈理论,采用基于继电反馈的PID控制的方法,设计飞行姿态模拟器的自适应控制器,并给出控制器参数和实验效果。通过理论分析和实验验证,证明自适应控制算法在飞行器控制方面的有效性和针对变负载下的自适应性,同时说明了飞行姿态模拟器是研究自适应控制和飞行器控制的非常理想的实验平台。
关键词:飞行器控制;自适应控制;继电反馈原理;PID控制;参数自整定
中图分类号:TP 273
文献标志码:A
文章编号:1007-449X(2018)04-0105-08
Abstract:In this paper, a two-degree-of-freedom flight attitude simulator with variable load is used as an experimental platform to study the adaptive control of aircraft under varying loads.According to the theory of relay feedback, PID controller was used to design the adaptive controller for this simulator, and the controller parameters and experimental were given.Through theoretical analysis and experimental verification, it is proved that the adaptive control algorithm is effective in aircraft control and adaptive to variable loads.It also shows that the flight attitude simulator is an ideal experiment platform to study adaptive control and aircraft control.
Keywords:aircraft control; adaptive control; principle of relay feedback; PID control; self-tuning of parameters
0 引 言
微小型旋翼式飞行器在军民领域有着极其重要的应用价值。由于旋翼式小型飞行器具有垂直起降的功能,并且具有易于制作、易于遥控以及成本相对低廉的特点,因而被广泛应用于娱乐、空中监视、搜救以及控制理论研究等方面。国内外一些知名高科技企业,已经生产出一系列各项性能优异的微小型旋翼式飞行器。
自2005年起,包括中国、德国、美国、法国在内的多个国家的高科技企业都先后开发出了自己的小型旋翼产品。不仅如此,国内外许多科研院所也围绕微小型旋翼式飞行器展开了各项研究。
2012年2月,宾夕法尼亚大学的韦杰·库玛教授展示了四旋翼的灵活编队操作[1]。2013年底,3D Robotics公司联手苏黎世联邦理工学院的PX4开源飞控开发团队,推出Pixhawk硬件。国内高校,清华大学、香港科技大学和北京航空航天大学等多所高校近年来对旋翼无人飞行器都有相关研究并取得一定进展。
为了有效提高姿态控制系统的研发效率和降低研发成本,旋翼式飞行模拟器应运而生,成为研制飞行控制系统和姿态控制系统中不可或缺的实验装置。这些装置将为研究飞行器的自主控制提供一个高效且低成本的研究平台。为此,一些公司和高校都在设计并开发这种飞行模拟产品。
直升机模型中比较有代表性的就是多伦多大学的方案。该方案中使用了TSK Mystar 60 作为模型直升机,并将该直升机固定在特殊结构的框架上实现直升机二自由度或者三自由度的姿态模拟[2]。不仅如此,2009年多伦多大学还和香港科技大学合作研制了一款直升机模拟器[3-4]。此方案也是以模型直升机为主体并辅助以支架,同时使用MEMS元件测量模拟器的姿态,进而实现对姿态的控制。
波黑萨拉热窝市的萨拉热窝大学电气工程学院的直升机模拟器方案比较新颖[5-6]。这个团队使用的直升机模型是Humusoft公司的一款產品,但是新颖之处在于他们使用了Matlab中的虚拟现实工具箱来对直升机建模,实验过程更简便、安全。
此外,研制旋翼式微小型飞行模拟器比较出名的公司有深圳固高公司,加拿大的Quanser公司,捷克Humusoft公司以及英国的Feedback公司。
深圳固高公司开发了一款三自由度直升机模拟器。系统提供了基于Matlab/Simulink的控制算法研究平台。Quanser公司开发了一款二自由度直升机模拟器,该模拟器使用信息采集卡作为传感器。Humusoft公司和Feedback公司也开发了自己的硬件设备。
本文提出了一种适合在实验室环境下研究旋翼式微小型飞行器姿态控制的小型二自由度飞行姿态模拟器。同已有的方案相比,此套设备本体结构不同,而且可以方便地改变整个系统的质心位置,从而改变被控对象的动力学方程中的参数。这使得在不同的俯仰角附近,模拟器的动力学特性的稳定性不同。这为研究强鲁棒性、自适应姿态稳定以及大角度姿态调整控制问题提供了一个良好的实验平台。
本文同时建立了俯仰通道的动力学模型,详细分析了俯仰通道的动力学特性,设计了俯仰通道的参数自适应整定控制规律,并最终通过实验验证了自适应整定算法的有效性以及针对变负载系统的控制器参数自整定的能力。
1 整体方案与动力学模型
1.1 结构设计与坐标系建立
飞行姿态模拟器的外形结构如图1所示。机械结构包含底座、支撑杆和摆动臂三部分。摆动臂两端安装各安装一个电机,两个电机方向垂直,电机上安装有螺旋桨,用来给摆动臂提供驱动力。
图中:F1为俯仰方向螺旋桨升力,垂直摆杆向上;F2为偏航方向螺旋桨升力,垂直指向纸面外,l为配重铜块到支点距离;L为俯仰通道摆动力臂长度;mg为配重块所受重力。
1.2 俯仰通道动力学模型的建立
若只考虑俯仰通道的动力学模型,可以将空间运动简化为平面运动,参见图2。定义水平位置为0位置点,逆时针旋转(图中向上)为正方向。根据平面运动中刚体绕定点运动的规律,可以得到飞行姿态模拟器的俯仰通道动力学模型为
其中:φ为摆动臂的俯仰角;J为整条摆动臂对O点的转动惯量;k为角速度阻尼系数。系统的机械参数如表1所示。
本系统是一个非线性被控系统。若将非线性部分在某一点处线性化,得到的是一个二阶线性定常系统。线性化点不同,系统的开环稳定性也会不同。
1.3 PWM占空比“p”和螺旋桨升力“F1”函数关系
理论建模中,动力学方程(1)所代表系统的输入为螺旋桨提供的升力。但实际系统中,螺旋桨是靠电机驱动,而电机转速和螺旋桨升力之间会有一定的函数关系。理想情况下,升力和转速的平方成正比。
此外,本系统采用的电机为无刷直流电机,调速方式为PWM调速,理论上PWM占空比和转速之间为线性关系。但实际系统中PWM占空比和转速之间的关系不会是很理想的线性关系。由此,“占空比”和“螺旋桨升力”之间存在一个非线性的函数关系。此处,忽略了“占空比”到“电机转速”以及“电机转速”到“螺旋桨升力”之间的动态过程,将之近似为一静态非线性函数关系,即
其中:p为无量纲的“占空比”;f(·)表示“占空比”和螺旋桨升力之间的静态非线性函数关系。
通过实验测试与数据拟合得到式(2)的静态非线性函数关系。首先得到了“占空比”和转速之间的关系,在此基础上通过实验测试得到了“转速”和“螺旋桨升力”之间的关系。
1.3.1 PWM占空比和转速的实验测试
实验时,由于俯仰通道的电机正转、反转特性不尽相同,因此会得到俯仰电机正转、反转两条拟合曲线。散点图及拟合图如图3所示。
其中:N代表电机转速,单位为转每分钟(r/min)。式(3)中,占空比p取負值;式(4)中,占空比p为正。占空比的符号代表电机旋转的方向。
1.3.2 转速和升力的实验测试
电机转速与升力关系测试原理如图4所示。
系统平衡时的关系式为
实验时,在某一转速下调整配重位置,稳定后根据式(5)计算该转速下的螺旋桨升力,多次测量。然后占空比增加5%,重复上述操作。最后得到占空比以5%为步长的、从20%到100%对应转速下的螺旋桨升力散点图及曲线拟合图,参见图5。
在无其他干扰的情况下,螺旋桨提供的升力与转速的一至三次方成正比。经过实验,发现二次函数拟合的效果最好。曲线对应的函数关系如式(6)所示。
1.4 PWM占空比和升力的实验测试
进一步地,可以得到PWM占空比p和升力F之间的关系。散点图及曲线拟合图参见图6,相应的函数解析表达式参见式(7)和式(8)。
2 姿态稳定自整定PID控制律设计
对于本文描述的飞行姿态模拟器,为了实现姿态稳定控制,一个工程易行的方法就是PID控制。实际使用时,只需要调节比例、微分和积分三个系数即可。一般来讲,需要人为整定三个比例系数。本文中,针对具体的被控对象,设计并实现了一个自整定PID算法。
2.1 自整定PID控制律原理
本文使用继电反馈的方式实现PID控制器的自整定[7]。继电环节的特点就是会使系统产生振荡。用描述函数法分析,如果被控对象的Nyquist图和非线性环节的负倒描述函数有交点,并且交点对应一个稳定的极限环,系统就会产生等幅振荡。为减弱噪声的影响,使用的是带有一定滞环宽度的继电反馈特性,相应的奈氏图及继电负倒描述函数示意图如图7所示。
按照描述函数分析方法,图中A点对应一个稳定的极限环。继电环节在该点处的描述函数幅值对应被控对象的临界增益;极限环振荡的周期对应被控对象振荡的周期。得到这两个关键参数后可以使用strm继电整定法整定PID参数。
2.2 系统内环初步镇定控制律设计
继电反馈整定方法多用于工业控制,最理想的作用模型是FOPDT(First Order Plus Delay Time)模型。本文中的二自由度飞行姿态模拟器在水平位置线性化后的模型的特性与FOPDT模型有较大差异。为了能够顺利实现自整定控制律,需要设计内环控制器从而改善被控对象的动态响应特性。
考虑到不论具体参数如何,二自由度飞行姿态模拟器在水平位置线性化之后的数学模型具有如下形式:
可以看出,不论原始对象的参数如何,都能够选择合适的Kd,Kp,将系统的特征根配置到期望位置。
根据具体的物理参数,取时域指标ts=1s,ξ=2,根据时域指标经验公式计算出PD控制器参数为
此时,设定点为0度的被控对象闭环阶跃响应曲线如图8所示。
2.3 自整定PID 控制律设计
自整定PID控制器的系统框图如图9所示。
设计时根据strm整定规则,可以选择继电环节滞环宽度ε=0.164 8,上饱和输出d=0.5。对应继电环节的负倒描述函数为
此时被控对象的Nyquist图与继电环节的负倒描述函数曲线图如图10所示。
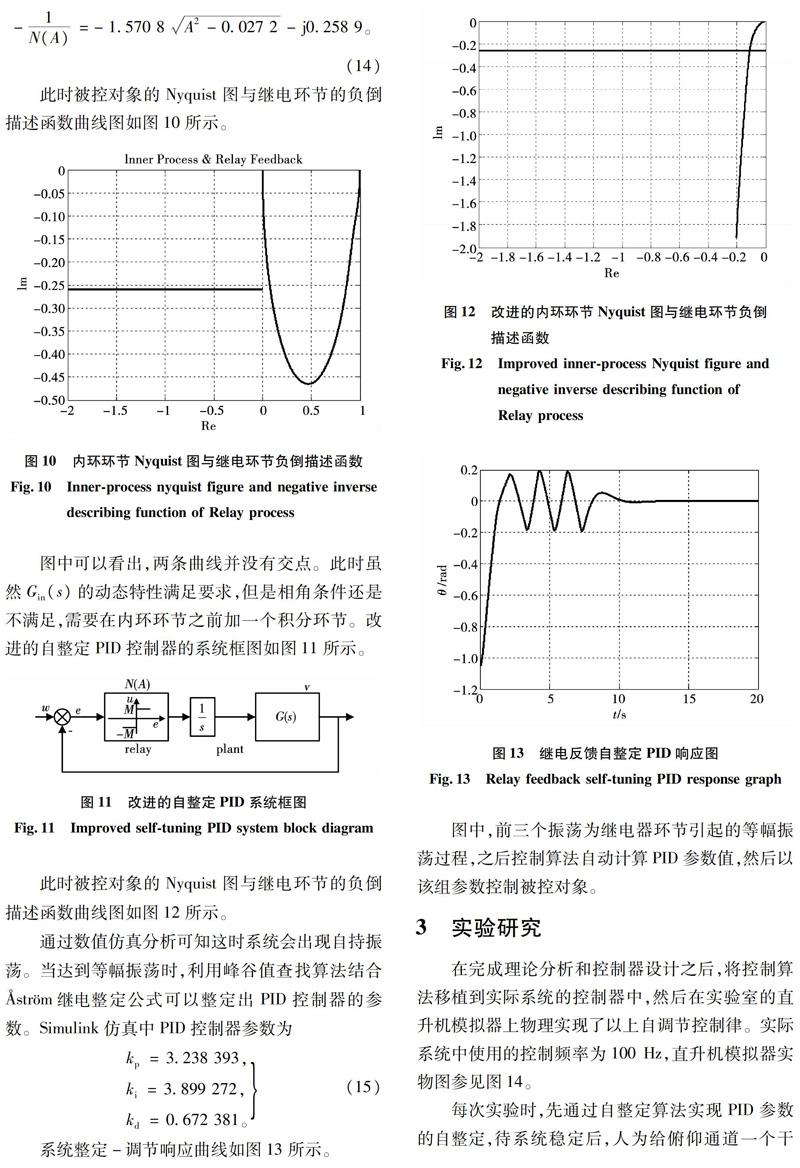
图中可以看出,两条曲线并没有交点。此时虽然Gin(s)的动态特性满足要求,但是相角条件还是不满足,需要在内环环节之前加一个积分环节。改进的自整定PID控制器的系统框图如图11所示。
此时被控对象的Nyquist图与继电环节的负倒描述函数曲线图如图12所示。
通过数值仿真分析可知这时系统会出现自持振荡。当达到等幅振荡时,利用峰谷值查找算法结合strm继电整定公式可以整定出PID控制器的参数。Simulink仿真中PID控制器参数为
系统整定-调节响应曲线如图13所示。
图中,前三个振荡为继电器环节引起的等幅振荡过程,之后控制算法自动计算PID参数值,然后以该组参数控制被控对象。
3 实验研究
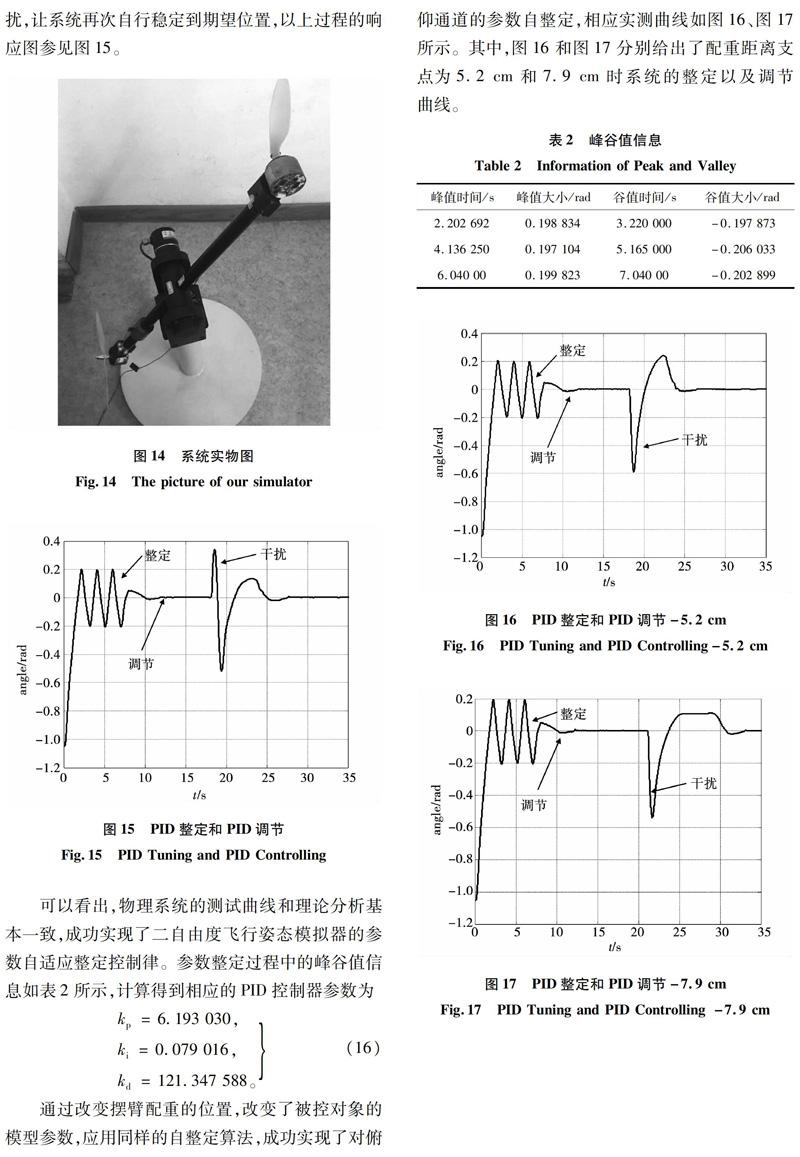
在完成理论分析和控制器设计之后,将控制算法移植到实际系统的控制器中,然后在实验室的直升机模拟器上物理实现了以上自调节控制律。实际系统中使用的控制频率为100 Hz,直升机模拟器实物图参见图14。
每次实验时,先通过自整定算法实现PID参数的自整定,待系统稳定后,人为给俯仰通道一个干扰,让系统再次自行稳定到期望位置,以上过程的响应图参见图15。
可以看出,物理系统的测试曲线和理论分析基本一致,成功实现了二自由度飞行姿态模拟器的参数自适应整定控制律。参数整定过程中的峰谷值信息如表2所示,计算得到相应的PID控制器参数为
通过改变摆臂配重的位置,改变了被控对象的模型参数,应用同样的自整定算法,成功实现了对俯仰通道的参数自整定,相应实测曲线如图16、图17所示。其中,图16和图17分别给出了配重距离支点为5.2 cm和7.9 cm时系统的整定以及调节曲线。
4 结 论
本文设计了一种适合在实验室环境下研究旋翼式微小型飞行器姿态控制的二自由度飞行姿态模拟器。该模拟器为研究强鲁棒性、自适应姿态稳定的控制问题提供了一个良好的实验平台。在此基础上本文设计了俯仰通道的PID参数自整定控制规律,并最终通过实验验证了自适应整定算法的有效性以及针对变负载系统的控制器参数自整定的能力。
参 考 文 献:
[1] M SCHWAGER, N MICHAEL, V KUMAR ,et al.Time scales and stability in networked multi-robot systems[C]//Shanghai :2011 IEEE International Conference on Robotics and Automation, 2011.
[2] S A BORTOFF.The University of Toronto RC helicopter: a test bed for nonlinear control[C]//Kohala Coast: Proceedings of the 1999 IEEE International Conference on Control Applications (Cat.No.99CH36328), HI, 1999.
[3] SONG B, MILLS J K, HUANG H, et al.Nonlinear robust control of a small-scale helicopter on a test bench[J].International Journal of Control, 2010, 83(4): 761.
[4] SONG B, MILLS J K, LIU Y, et al.Nonlinear dynamic modeling and control of a small-scale helicopter[J].International Journal of Control, Automation and Systems, 2010, 8(3): 534.
[5] A.Badnjevic', E.unic', T.Uzunovic' and N.Osmic'.Design and implementation of three-dimensional simulator for control of laboratory model helicopter[C]//Opatija, Croatia: The 33rd International Convention MIPRO, 2010.
[6] J.Velagic, N.Osmic, E.Zunic,et al.Badnjevic.Design of 3D simulator for 2DOF helicopter model control[C].Zadar: Proceedings ELMAR-2010, 2010.
[7] Karl Johan Astrom, Bjorn Wittenmark.Adaptive Control[M]: New York: Dover Publications, INC, Mineola,2008.375-388.
(編辑:刘素菊)
