铁心电抗器气隙边缘效应计算及影响因素

官瑞杨 魏新劳 王永红 陈庆国

摘 要：提出一种用于计算气隙等效导磁面积的方法：用有限元法计算自感，将漏感从仿真所得自感中扣除，再结合主电感理论公式反推出气隙等效导磁面积扩大系数。分析了电感参数及ANSYS计算原理；结合对比文献论证了本方法的优越性；实验和仿真验证了该方法的正确性；定性分析气隙边缘效应的影响因素。研究结果表明：主要影响因素依次为气隙长度、铁心截面积、铁心相对磁导率，且气隙长度起主导作用；气隙等效导磁面积扩大系数与气隙长度呈正比，与铁心截面积和相对磁导率呈反比。本方法有效避免了漏电感的影响，所得结论可为铁心电抗器的设计提供参考依据。

关键词：铁心电抗器；边缘效应；气隙；等效导磁面积；电感

中图分类号：TM 47

文献标志码：A

文章编号：1007-449X（2018）04-0081-08

Abstract：A method is proposed for calculating air-gap equivalent cross-sectional area.The finite element method was used to calculate the self-inductance，and the leakage-inductance was deducted from the self-inductance simulated.With the main-inductance′ formula， it deduced the air-gap equivalent cross-sectional area coefficient′s expression. Different kinds of inductances and ANSYS calculation theory were analysed. This method′s superiority was demonstrated by comparing with the reference. Experiments and simulations confirm the correctness. Qualitative analysis of influence factors of air-gap edge effect was made. Research results showed that main influence factors include air-gap， iron′s cross-sectional area and iron′s relative permeability. The air-gap plays a leader role. The relationship between air-gap equivalent cross-sectional area coefficient and air-gap is a proportional function， while the relationship is an inverse proportional function with iron′s cross-sectional area or iron′s relative permeability. This method can avoid the leakage-inductance′s influence and the results provide some references for designing iron-core reactor.

Keywords：iron-core reactor； edge effect； air-gap； equivalent cross-sectional area； inductance

0 引 言

铁心电抗器是电力系统中很重要的电气设备之一，在补偿无功功率、提高电能质量、抑制短路电流等方面具有广泛应用[1-3]。因此，为了满足不同场合的需求，必须设计具有特定电感值（无功功率）的电抗器。铁心电抗器电感值设计越精确，其运行效果越好，越能满足电力系统的需求，进而提高电网运行稳定性。

然而，在铁心电抗器的设计计算中，电感值受气隙边缘效应的影响很大，微小的气隙变化很可能造成电感值很大偏差[4]。原因在于：當磁通流经铁心中的气隙时发生“衍射”现象，即磁力线有发散的趋势，造成气隙等效导磁面积（磁通截面积）扩大化。具体扩大的程度与气隙长度、铁心直径等因素密切相关。因此可以说，能否正确、可靠地计算出铁心电抗器气隙等效导磁面积直接影响到电感值的计算精确度。

由于目前没有完备的实验数据可供参考，在铁心电抗器的生产过程中需要反复调整气隙的大小才能得到满意的电感值。关于气隙等效导磁面积计算的文献也很少：以往的经验公式是基于气隙处半圆形的简化磁路，气隙等效导磁面积扩大系数约在1.1～1.3之间[5]，该经验公式只能粗略估算、具有较大误差；文献[6]和文献[7]在理论上以求解电磁方程的方法计算气隙等效导磁面积扩大系数，可为铁心电抗器的设计提供理论依据，然而其求解模型具有特定约束条件，应用于实际铁心电抗器生产中难免产生偏差。文献[8]计算气隙等效导磁面积时所用电感值包含了漏电感，因此计算精度不高。

本文提出一种用于计算气隙等效导磁面积的方法：运用ANSYS软件仿真计算铁心电抗器的电感参数，依据电力变压器漏电感的理论计算公式，将漏电感从仿真所得的自感中扣除，避免了漏电感对计算气隙等效导磁面积的影响，再结合主电感计算公式，反推计算出气隙等效导磁面积扩大系数。通过与参考文献的对比，论证了本文计算方法的优越性；利用ANSYS软件对三维电磁场仿真模型局部变化的敏感性，得出气隙等效导磁面积的影响因素：气隙长度、铁心截面积和铁心相对磁导率，并作定性分析。仿真结果与实验测量的数据相吻合，证实仿真模型及方法的正确性。鉴于目前计算机技术的发展，有限元数值计算的方法完全可以模拟真实情况下铁心电抗器的工作状态，笔者认为本文结果具有较好的实际性，可为铁心电抗器的设计提供一定参考依据。

1 计算方法

1.1 电感参数

电感是铁心电抗器的主要电气参数之一，电感参数的定义根据其交流磁通形成的闭合回路不同而对应不同的电感名称（主电感和漏电感）。对于单线圈铁心电抗器而言，线圈产生的交流磁通分为两部分：一部分是通过铁心磁路（由铁心及气隙组成）中的磁通，该部分为线圈产生磁通的主要部分，称为主磁通，它对应的电感叫主电感；另一小部分磁通经过线圈外的非铁磁性材料闭合，称为漏磁通，它对应的电感叫漏电感。把主电感与漏电感之和称为线圈的自感。

实验样机是一台干式铁心电抗器，采用双线圈的形式，两个线圈同向串联（互相增磁）。除了具有上述两种电感之外，两个线圈之间还有互感（如果看成一个线圈，互感包含于自感当中）。图1为实验样机，图2为双线圈铁心电抗器磁通分布示意。

从图2的磁通分布可以看出：受气隙边缘效应影响，主磁通在气隙处发生了“衍射”现象，该处存在气隙等效导磁面积扩大的问题；而漏磁通并不经过该气隙，因此不涉及气隙等效导磁面积计算的问题，需要将漏电感排除。气隙等效导磁面积的计算仅与主电感值有关。

双线圈同向串联时，铁心电抗器的主电感公式为

从式（4）可以看出：在结构参数已知的情况下，如果能够准确计算出电抗器的总电感L和漏电感Lσ，则可以反推出气隙等效导磁面积扩大系数。在本文中，电抗器的总电感L采用电磁场数值计算的方法计算，而线圈漏电感Lσ的计算则采用电力变压器设计的理论公式计算[9-13]。还可以看出：铁心电抗器气隙等效导磁面积扩大系数计算式是一个随多元参数变化的函数，例如受气隙长度lq、铁心截面积S0、铁磁材料相对磁导率μr等参数的影响。

用于计算漏电感的理论公式如下：

式中：ρ为洛氏系数；AQ为漏磁通等效导磁面积；HL为线圈高度；BH为线圈厚度；RW为线圈外半径；RN为线圈内半径；AZ为铁心有效截面积；kdp为叠片系数；DW为线圈外半径；D为铁心直径。

1.2 ANSYS计算电感

有限元法从Maxwell电磁场方程出发，构建铁心电抗器三维仿真模型[14-17]，并结合以下假设条件：

1）求解模型内电磁场属于似稳场且当做恒定磁场；

2）铁心材料为均匀、线性、各向同性媒质；

向量磁位A满足的边值方程为：

式中：向量磁位A=[Ax，Ay，Az]T；Ω为整个求解域；传导电流密度J=[Jx，Jy，Jz]T；S1为模拟无穷远边界；S2为铁心材料与空气材料的衔接面；K为衔接面面电流密度；μ为磁导率。

再根据条件变分原理，把式（6）转化为等价的条件变分方程，然后把求解域剖分为有限个单元，利用插值函数将条件变分方程离散化，得出一组以节点向量磁位为变量的代数方程组并结合相应的边界条件进行求解。

ANSYS软件在求解铁心电抗器的自感时，是从能量角度进行分析，磁场能量与电感值满足关系式：

式中：Wm为整个计算场域中的磁场能（算出的电感值L为电抗器的总电感）；I为线圈所加激励电流有效值。由于已经假设为均匀、线性媒质，磁场能量Wm又可表示为：

式中：B为对应媒质内的磁感应强度，其值为向量磁位的旋度；H为磁场强度；V为对应媒质区域的体积。

考虑到有限元方法的离散化，式（8）的磁场能量应该为铁心材料及非铁磁性材料中各个剖分单元的磁场能量和（离散积分）。可表示为

式中：Bi为剖分单元内的平均磁感应强度，dvi为剖分单元的体积，μri为dvi内对应材料的相对磁导率；

2 样机仿真

为验证本文仿真模型及计算方法的正确性，以图1中的实际干式铁心电抗器为例，用仿真计算的电感值与实际测量值相对比。实验样机具体结构参数见表1。

单元类型选为solid117单元（棱边单元法），铁心材料相对磁导率设定为2 000，线圈和空气模型的相对磁导率设为1，采用稀疏矩阵求解器，运用LMATRIX宏命令即可求得电抗器的电感值。图3为该电抗器三维仿真模型单元剖分图。图4给出了磁感应强度矢量图。

从图4可以看出：磁感应强度分布情况与基本理论相一致，铁心中的磁感应强度明显高于外围空气中的磁感应强度，同时可清晰看出鐵心回路中气隙处发生了磁通的衍射现象。表2给出了实验测量的电感值与仿真计算电感值。电感测量设备选为日本HIOKI公司生产的3532-50 LCR测试仪，它是一个频率在42 Hz～5 MHz之间，可同时测量L、C、R的高精度测试设备。

综上分析，可以充分证明仿真模型及计算方法的正确性和可行性。

3 优越性及应用场合

为说明所得数据的参考价值及计算方法的优越性，下面与文献[6]进行对比分析。文献[6]从基本理论的角度求解电磁方程来计算气隙等效导磁面积扩大系数，并给出了部分数据。

首先以文献[6]中给出的一组数据为例，与本文计算方法做对比。表3列出了以铁心直径为300 mm，气隙长度为50 mm，线圈匝数为186匝的铁心电抗器分别采用两种方法得到的气隙等效导磁面积扩大系数及电感参数。

从上表可以看出文献[6]给出的气隙等效导磁面积扩大系数存在一定偏差，导致设计计算的电感值也有偏差。为了说明数据的普遍性，文献[5]对文献[6]的数据进行拟合，得到气隙等效导磁面积扩大系数的表达式：

式中，各个符号的意义均与上文相同。于是可以计算出铁心直径为110 mm，气隙长度从1 mm到50 mm时气隙等效导磁面积扩大系数，见表4。图5给出了用两种方法所得气隙等效导磁面积扩大系数的曲线。

从上图可以看出：当气隙小于10 mm时，文献[6]中的数据与本文计算方法得出的气隙等效导磁面积扩大系数基本一致；随着气隙的增大，文献[6]中的数据偏差逐渐增大。由于本文计算的数据已经用于设计实际样机，并且得到了实验测试结果和仿真的证实，可以充分说明本文方法与其他理论计算方法相比具有优越性。

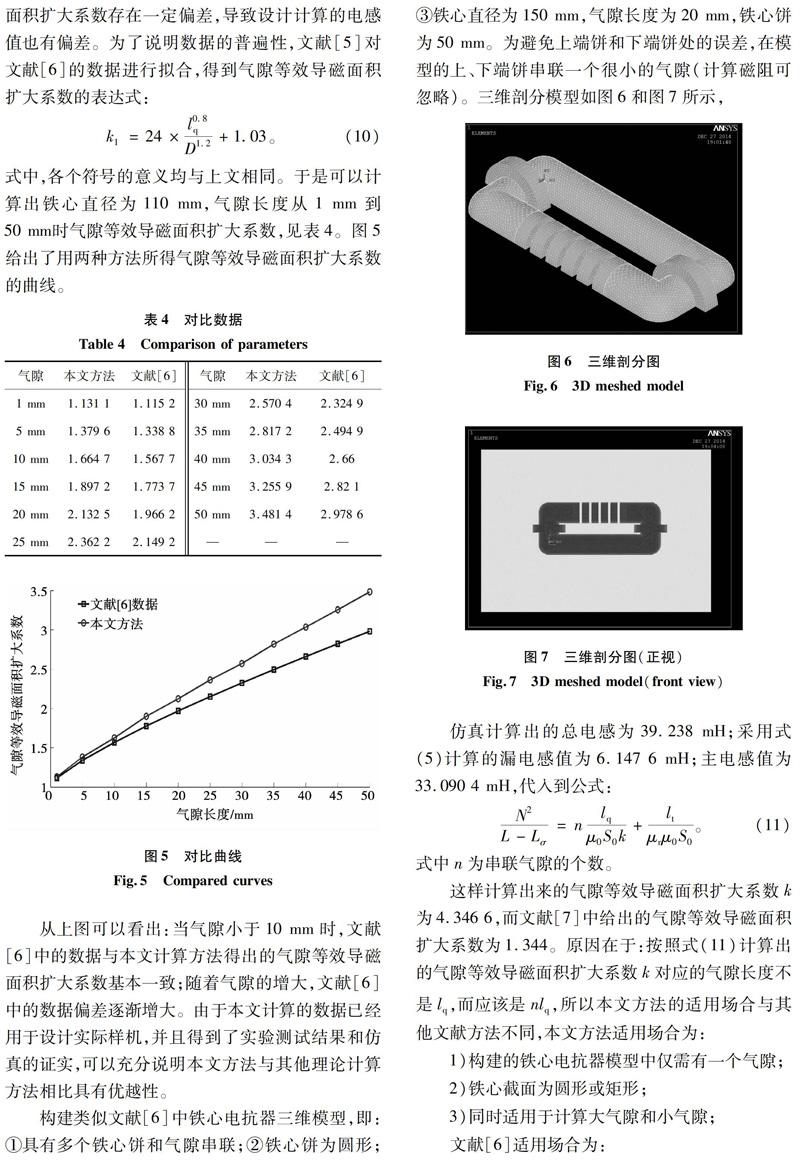
构建类似文献[6]中铁心电抗器三维模型，即：①具有多个铁心饼和气隙串联；②铁心饼为圆形；③铁心直径为150 mm，气隙长度为20 mm，铁心饼为50 mm。为避免上端饼和下端饼处的误差，在模型的上、下端饼串联一个很小的气隙（计算磁阻可忽略）。三维剖分模型如图6和图7所示，

仿真计算出的总电感为39.238 mH；采用式（5）计算的漏电感值为6.147 6 mH；主电感值为33.090 4 mH，代入到公式：

这样计算出来的气隙等效导磁面积扩大系数k为4.346 6，而文献[7]中给出的气隙等效导磁面积扩大系数为1.344。原因在于：按照式（11）计算出的气隙等效导磁面积扩大系数k对应的气隙长度不是lq，而应该是nlq，所以本文方法的适用场合与其他文献方法不同，本文方法适用场合为：

1）构建的铁心电抗器模型中仅需有一个气隙；

2）铁心截面为圆形或矩形；

3）同时适用于计算大气隙和小气隙；

文献[6]适用场合为：

1）无穷多个铁心饼与气隙串联，且仅适用中间段的气隙（局限性：实际铁心电抗器铁心饼个数很少）；

2）铁心截面为圆形（局限性：实际铁心截面为多级梯形或者为矩形）；

3）计算模型气隙处磁力线只在相邻铁心饼之间跨越（局限性：过于简单化与理想化，仿真结果可以看出磁力线不仅仅只在相邻的铁心饼之间跨越）；

4）气隙的磁位分布用二次函数假设逼近。

即使本文方法构建的铁心电抗器模型中仅需有一个气隙。但本文方法计算所得的k依然可以用于设计具有多个气隙和铁心饼串联的场合，这一点可以得到仿真的证实，下面结合一个例子说明。本文方法计算出气隙长度为10 mm，铁心截面积为5 024 mm×mm（对应铁心直径80 mm）时，气隙等效导磁面积扩大系数为2.126 7。将该系数用于设计具有两个气隙的铁心电抗器所得结果见表5。

4 影响因素

4.1 气隙长度

利用控制变量法和ANSYS软件对仿真模型结构变化的敏感性，仿真计算出大量数据（电感值），并结合公式（4）研究气隙等效导磁面积扩大系数与气隙长度的关系。从公式（4）可以看出：气隙等效导磁面积扩大系数与气隙长度lq呈正比关系。该关系可以在图8中得到进一步证实。

图8给出了铁心截面积分别为5 024 mm2、6 358 mm2、7 850 mm2和9 498 mm2时的4条曲线（对应铁心直径从80 mm到110 mm），每条曲线趋势基本为正比例关系；且铁心截面积越大时，曲线斜率越小。这一点可以理解为：铁心截面积大时，铁心有足够的空间可供磁通流过，边缘效应小。

4.2 铁心截面积

把公式（4）整理成气隙等效导磁面积扩大系数与铁心截面积的关系式：

可以看出：气隙等效导磁面积扩大系数与铁心截面积呈反比关系，如图9所示。

上图给出了气隙长度分别为5 mm、10 mm和15 mm时，气隙等效导磁面积扩大系数随铁心截面积的增大而减小；这三条曲线中，气隙长度大的曲线位于上方。这一点可以理解为：气隙长度起主导作用，气隙越大，边缘效应越大。

4.3 铁心相对磁导率

由式（4）分母最后一项可知，当认为铁心相对磁导率为无穷大或者铁心磁路等效长度lt很小（lt远小于μr）时，可以忽略铁心材料的磁阻，此时气隙等效导磁面积扩大系数与铁心相对磁导率无关。然而，在实际工作的设备中，铁心磁路长度lt为一定值，或者铁心出现饱和时相对磁导率不是无穷大值，这时就不能忽略铁心相对磁导率对气隙等效导磁面积的影响，如图10所示。

图10给出铁心直径为80 mm、气隙长度为1 mm时，气隙等效导磁面积扩大系数随铁心相对磁导率增大而减小，该曲线陡度也不断减小逐渐趋于稳定。这一点可以理解为：铁心相对磁导率很大时，对磁力线的“吸引”很强，边缘效应小；当铁心饱和或者趋于饱和时，铁心相对磁导率减小，边缘效应增强。还可以看出：即使铁心相对磁导率变化范围很大（从1 000到10 000），气隙等效导磁面积扩大系数的变化范围却很小（从1.362 8到1.156 2）。这可以认为：相比于其他影响因素而言，铁心相对磁导率不是主要影响因素。

4.4 综合因素

为更形象描述各种因素对气隙等效导磁面积的综合影响，本文给出了k的三维曲面图，如图11所示。铁心电抗器电感值的三维曲面图，如图12所示。

5 结 论

本文所提出用于计算气隙等效导磁面积的方法可有效避免漏电感的影响，提高了计算精确度；该方法的正确性得到了实验和仿真的证实；气隙边缘效应的主要影响因素依次为：气隙长度、铁心截面积和铁心相对磁导率，影响程度：气隙长度>铁心截面积>铁心相对磁导率；k与lq呈正比关系，k与S0和μr呈反比关系。

参 考 文 献：

[1] LIU Wenye，LUO Longfu，DONG Shuda. The summarize of power controllable reactor technology[C]//2010 the 3rd International Conference on Power Electronics and Intelligent Transportation System，2010：29-33.

[2] 周勤勇，郭強，卜广全. 可控电抗器在我国超/特高压电网中的应用[J]. 中国电机工程学报，2007，27（7）：1.

ZHOU Qinyong， GUO Qiang， BU Guangquan. Application of controllable reactors in Chinas power grid at extra and ultra voltage level[J]. Proceedings of CSEE， 2007，27（7）：1.

[3] 孔宁，尹忠东，王文山，等. 电抗器的可控调节[J]. 变压器，2011，48（5）：33.

KONG Ning， YIN Zhongdong， WANG Wenshan， et al. Controllable adjustment of reactor[J]. Transformer，2011，48（5）：33.

[4] 官瑞杨. 磁楔式可调电力电抗器研制[D]. 哈尔滨：哈尔滨理工大学，2015.

[5] 姜宏伟，李景禄，宋国福，等. 气隙调感式消弧线圈结构设计及计算[J]. 变压器，2002，39（2）：5.

JIANG Hongwei， LI Jinglu， SONG Guofu，et al. Calculation and structural design for air gap inductance regulation arc-suppression coil[J]. Transformer， 2002，39（2）：5.

[6] 潘三博，陈乔夫. 大气隙铁心电抗器气隙等效导磁面积计算[J]. 变压器，1998，35（3）：11.

PAN Sanbo， CHEN Qiaofu. Equivalent cross-sectional area calculation of gaps in core reactor with big gaps[J]. Transformer，1998，35（5）：11.

[7] 陈乔夫. 铁心电抗器气隙等效导磁面积的计算[J]. 变压器，1988：7.

[8] 官瑞杨，魏新劳，聂洪岩. 铁心电抗器气隙等效导磁面积计算[J]. 哈尔滨理工大学学报，2014，19（4）：6.

GUAN Ruiyang， WEI Xinlao， NIE Hongyan. The calculation of air gap equivalent cross-sectional area in core reactor[J]. Journal of Harbin University of Science and Technology，2014，19（4）：6.

[9] 朱英浩.油浸电力变压器设计手册[M]. 沈阳，沈阳变压器有限责任公司，1999：20-52.

[10] 魏新劳，官瑞杨. 磁楔式可调电抗器原理与分析[J]. 电机与控制学报，2015，19（11）：32.

WEI Xinlao， GUAN Ruiyang. Theory and analysis of magnetic-wedge adjustable reactor[J]. Electric Machines and Control， 2015，19（11）：32.

[11] LIANG Yanping，ZHANG Fang，ZHANG Haiting. Leakage inductance calculation and simulation research of extra-high voltage magnetically controlled shunt reactor[C]//2010 International Conference on Mechanic Automation and Control Engineering，Shenyang，China，2014.

[12] 趙亮，张建军，梁东. 干式带气隙铁心电抗器电感计算方法[J]. 高压电器，2012，48（6）：61.

ZHAO Liang， ZHANG Jianjun， LIANG Dong. Inductance calculation method for dry-type gapped-iron reactor[J]. High Voltage Apparatus， 2012，48（6）：61.

[13] 朱宝森，关毅，陈庆国，等. 正交磁化可控电抗器的设计与特性分析[J]. 电机与控制学报，2012，16（5）：26.

ZHU Baozen， GUAN Yi， CHEN Qingguo. Design and characteristics analysis of orthogonal magnetization controllable reactor[J]. Electric Machines and Control， 2012，16（5）：26.

[14] 杨平，朱涤心，等. 近代电磁场理论[M]. 哈尔滨，哈尔滨理工大学，2004：1-37.

[15] 杜华珠，文习山，鲁海亮，等. 35kV三相空心电抗器组的磁场分布[J]. 高电压技术，2012，38（11）：2858.

DU Huazhu， WEN Xishan， LU Hailiang， et al. Distribution of magnetic field for 3-phase air core reactor at 35kV[J]. High Voltage Technology，2012，38（11）：2858.

[16] YUAN Fating， YUAN Zhao， LIU Junxiang， et al. Research on temperature field simulation of dry type air core reactor[C]//2017 20th International conference on electrical machines and systems，2017.

[17] 谢龙汉，耿煜，邱婉. ANSYS电磁场分析[M]. 北京，电子工业出版社，2012：111-289.

（编辑：刘素菊）