关于矩阵方程AXB-C=0的最佳逼近解的一个注记

宋传宁 许庆祥

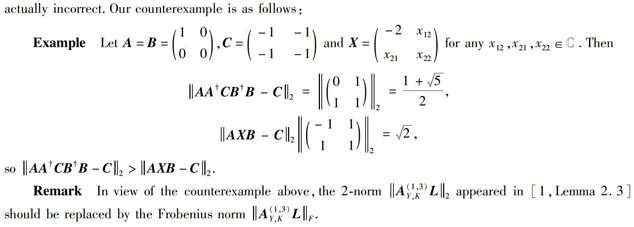
A note on the best approximate solution of the

equation AXB-C=0

Song Chuanning， Xu Qingxiang

（Mathematics and Science College，Shanghai Normal University，Shanghai 200234，China）

Abstract：

A counterexample is constructed which shows that with respect to the 2-norm，there exist matrices A，B and C such that A CB fails to be the best approximate solution of the equation AXB-C=0，where A and B are the Moore-Penrose inverses of A and B，respectively.

Key words：

Moore-Penrose inverse; Frobenius norm; 2-norm

CLC number： O 151.21Document code： AArticle ID： 1000-5137（2018）01-0022-02

摘要：

舉反例说明：对于矩阵的2-范数，存在矩阵A，B和C，使得ACB不是矩阵方程AXB-C=0的最佳逼近解，其中A和B分别是A和B的Moore-Penrose逆.

关键词：

Moore-Penrose逆; Frobenius 范数; 2-范数

Received date： 2017-02-25

Foundation item： The National Natural Science Foundation of China （11671261）

Biography： Song Chuanning（1962-），female，associate professor，research area：Matrix and operator theory.E-mail：songning@shnu.edu.cn

引用格式： 宋传宁，许庆祥.关于矩阵方程AXB-C=0的最佳逼近解的一个注记 [J].上海师范大学学报（自然科学版），2018，47（1）：22-23.

Citation format： Song C N，Xu Q X.A note on the best approximate solution of the equation AXB-C=0 [J].Journal of Shanghai Normal University（Natural Sciences），2018，47（1）：22-23.

Throughout this note，Cn×n is the set of n×n complex matrices.For any A∈ Cn×n，let A be its Moore-Penrose inverse[1-2].Let ·F and ·2 be the Frobenius norm and 2-norm （spectral norm） on Cn×n，respectively.

Definition

[2]Let · be any norm on Cn×n，and A，B，C be given in Cn×n.A matrix X0∈Cn×n is said to be the best approximate solution （with respect to the norm ·） of the equation F（X）=defAXB-C=0，if for any X∈Cn×n，either F（X）>F（X0），or F（X）=F（X0） and X≥X0.

It is known from [2，Corollary 1] that with respect to the Frobenius norm ·F，the matrix X0=ACB is the unique best approximate solution of the equation F（X）=0.A similar conclusion was asserted in item （b） of [1，Theorem 2.1] for the 2-norm.In this note，we will show that item （b） of [1，Theorem 2.1] is actually incorrect.Our counterexample is as follows：

Example

Let A=B=10

00，C=-1-1

-1-1 and X=-2x12

x21x22 for any x12，x21，x22∈C.Then

AACBB-C2=01

112=1+52，

AXB-C2-11

112=2，

so AACBB-C2>AXB-C2.

Remark

In view of the counterexample above，the 2-norm A（1，3）Y，KL2 appeared in [1，Lemma 2.3] should be replaced by the Frobenius norm A（1，3）Y，KLF.

References：

[1]Damm T，Stahl D.Linear least squares problems with additional constraints and an application to scattered data approximation [J].Linear Algebra and its Applications，2013，439：933-943.

[2]Penrose R.On best approximate solutions of linear matrix equations [J].Mathematical Proceedings of the Cambridge Philosophical Society，1956，52：17-19.