基于熵权法-TOPSIS模型的智慧城市评价研究
2018-05-14林莉冯爱芬丁真真李雪曼万凡王辰辰
林莉 冯爱芬 丁真真 李雪曼 万凡 王辰辰


[摘 要]随着智慧城市建设的迅速发展,智慧城市的评价成为一个热点问题。本文运用熵权法-TOPSIS模型,结合系统聚类的进一步分析,将12个城市依据各自的排名和突出特点分为4类,构建出了一套智慧城市建设综合性评价体系,对规范智慧城市的建设、推动智慧城市的健康发展具有重要意义。
[关键词]智慧城市;熵权法;TOPSIS综合评价法;系统聚类
[中图分类号]F299.2 [文献标识码]A
智慧城市评价体系是一套检验智慧城市建设程度的最直观体现,也是引导城市进行智慧化建设的索引,对智慧城市评价体系的研究具有重要的的科学价值和社会意义。近年,有很多学者对这个课题进行了研究,如:基于灰色关联理论和BP神经网络、运用投影追踪评价法、基于离差最大化的决策者权重的确定方法。目前有很多方法用来计算权重,如专家打分、熵权法、因子分析权数法等等。其中,熵权法计算权重取得了广泛的共识。因此本文拟采用熵权法-TOPSIS 评价法构建一套科学、成熟的智慧城市评价体系,并在实际问题中进行验证。
1 问题分析
通过研究调查发现,评价智慧城市的指标体系包括四个方面:科技水平、公共服务水平、经济水平、可持续发展水平。熵权法利用数据本身的信息量来确定指标的权重,有较强的数学理论依据。TOPSIS法是一种理想目标相似性的顺序优选技术,它通过计算出各目标的贴近度,并按贴近度大小进行排序,作为评价各目标优劣的依据。因此该文选用熵权-TOPSIS综合评价法对智慧城市评价体系进行研究,并给出合理建议。
2 样本选取与数据收集
本文选择华中地区部分代表性城市郑州、洛阳、南阳、开封、长沙、武汉等12个城市作为研究对象。本文的数据主要来源于各城市《2015年国民经济与社会发展统计公报》《环境状况公报》《中国城市统计年鉴2015》等官方文件,故数据的可信度较大。
3 构建评价指标体系
从智慧建设的基础角度出发看待问题,在选取的指标中,除了体现不同城市建设的特点,同时还应突出城市智慧的特点。根据以上角度的分析,建立本文智慧城市的评价体系,主要有三个层次组成:其中一级指标包括科技水平、公共服务水平、经济水平,可持续发展水平三级指标用x表示;科技水平:基本信息化:x1交通和通信占家庭消费比重、x2互联网用户普及率、x3移动电话普及率;公共服务水平,交通发展水平:x4交通运输投资占GDP比重、x5万人拥有公共交通车辆;教育发展水平:x6万人拥有专利数、x7财政性教育支出GDP比例、x8万人拥有大学生数量;医疗发展水平:x9每万人口医院床位数、x10每万人口医生数;经济水平,发展水平:x11人均GDP、x12第三产业增加值占地区生产总值比重;经济结构:x13GDP中第二产业贡献率、x14GDP中第三产业贡献率;消费水平:x15人均用水量(升)、x16年人均可支配收入;可持续发展水平,资源节约水平:x17综合能源消费总量(吨标煤)、x18森林覆盖率;环境保护水平:x19市区空气质量优良天数、x20工业固体废弃物综合利用率、x21工业用水重复率。
4 基于熵权-TOPSIS的智慧城市发展水平综合评价模型
4.1 基于熵权-TOPSIS的评价步骤
在m个被评价城市,n个评价指标的评估问题中,将第i个被评价城市在第j个指标上的原始指标值记为Uij(其中 i=1,2…m;j=1,2…n), 建立初始矩阵U=(uij)m×n。
4.1.1 原始数据的标准化处理
首先对指标值进行无量纲化处理消除量纲影响。对于正向指标负向指标分别通过最大最小化原则进行无量纲化处理,得到规范化矩阵X=(xij)m×n,xij为第i个被评价城市在第j个指标上的标准化值。
4.1.2 熵权法计算指标客观权重
(1)計算指标标准化值的比重 对标准化矩阵X=(xij)m×n中的各指标的标准化数据进行比重变换。利用公式计算对于第j个指标而言,第i个系统的贡献度pij。
(2)计算各指标的熵权值:其中,定义当pij=0时,pij ln pij=0。
(3)计算各指标的熵权重wj:
4.1.3 修正熵权重
本文引入基于专家打分的主观经验权重对客观熵权重进行修正,修正后的结合权重:
4.1.4 运用 TOPSIS 进行综合评价
构造标准化的数据加权决策矩阵将量纲化后的规范化矩阵x=(xij)m×n与修正后的指标权向量w0=(w1, w2, …, wn)相乘,如式,得到的标准化数据决策矩阵Y=(yij)m×n
(1)确定正理想解和负理解想
理想解A*是被评价系统中虚拟出来的、事实上并不存在的一个最优解,它其中的每一个指标值都是决策矩阵中该指标的最优值;负理想解A-则是最劣解,它其中的每一个指标值都是决策矩阵中的最差值。最优解和最劣解由下式确定,其中J=
(2)计算各评价对象指标的标准化向量分别到最优解和最劣解的欧式距离和,计算各评价城市指标与理想解的相对接近度,Ci值越大,表明该评价城市的智慧度越高;Ci值越小,表明该评价城市的智慧度越低。
4.2 基于熵权-TOPSIS模型的评价结果计算
4.2.1 计算组合权重
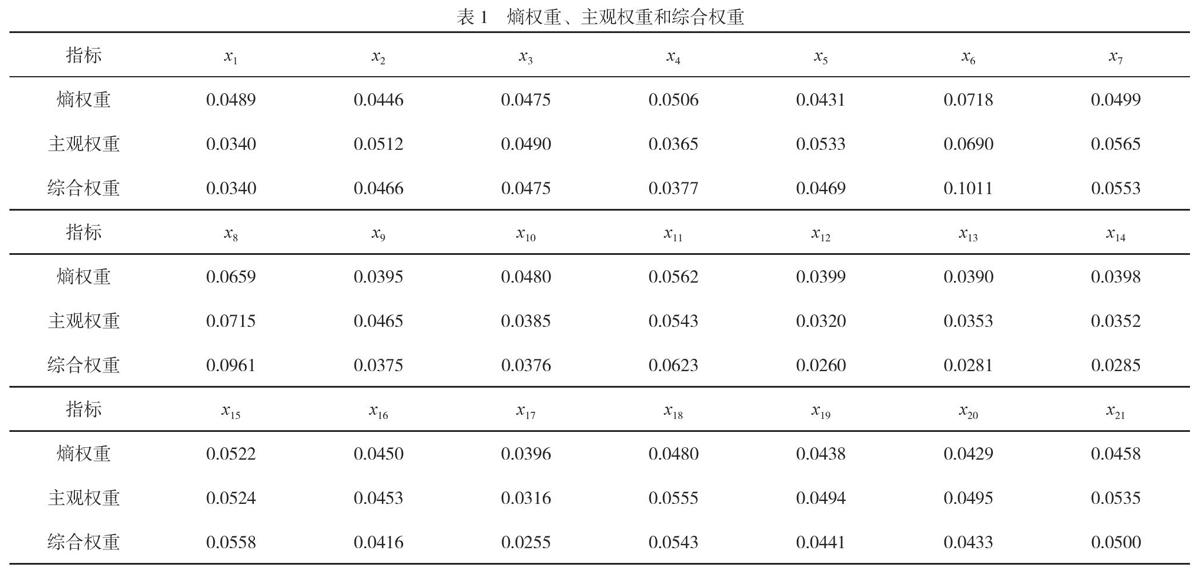
将12个城市21个指标的原始数据通过EXCEL计算处理得到21个指标的熵权重。结合专家打分的主观权重给出综合权重,计算结果见表1。
4.2.2 运用TOPSIS进行综合评价
结合各城市在各个指标下的标准化值以及表1中的综合权重,计算确定指标的理想解和负理想解。计算各城市方案离理想方案的欧式距离、离负理想方案的欧式距离以及各城市方案与理想方案的相对接近度。12个城市的智慧度从高到低依次为:长沙、武汉、郑州、宜昌、洛阳、荆州、黄冈、安阳、衡阳、漯河、南阳、开封。
从图1中可以找到这12个城市的归属类,进而以这12个城市的特点扩散到其他城市上,找到具有同一类特点的城市,对它们进行智慧度评测。
4.3 聚类分析
根据12个城市在科技水平、公共服务水平、经济水平和可持续发展水平4个维度的评价值采用聚类的方法进行聚类分析。希望通过找到城市的归属类型,对不同城市制定不同的发展计划,避免了以偏概全的盲目计划致使城市智慧化进程减慢或停滞。
依据12个城市的四个一级指标的TOPSIS评价得分,对它们进行系统聚类分析,根据树状图将它们分为四类:第一类城市是智慧水平优秀,公共服务水平最智慧的城市,包括长沙,武汉。第二类城市是智慧水平良好,科技水平最智慧的城市,包括郑州。第三类城市是智慧水平一般,可持续发展水平最智慧的城市,包括宜昌。第四类城市是总体智慧度一般的城市,包括洛阳、荆州、黄冈、安阳、衡阳、漯河、南阳、开封。
5 结语
经济环境及科技的不断变化,国内外智慧城市建设实践也会不断地发生变化,相应的评价指标体系也会做出相应的调整。本文的研究课题在设计上更加趋于严谨与科学。通过对智慧城市的研究,针对其智慧城市的发展程度,对相对欠缺的领域提出建议,对不同城市制定不同的发展计划,在一定程度上加快智慧城市的建设。
[参考文献]
[1] 包明林.基于BP神经网络的智慧城市发展潜力评价研究[D].湘潭大学,2016.
[2]廖胭脂,楼文高.智慧城市的投影寻踪评价模型与实证研究[J].中国发展,2017(02).
[3]马永红,周荣喜,李振光.基于离差最大化的决策者权重的确定方法[J].北京化工大学学报,2007(02).
[4] 巫细波,杨再高.智慧城市理念与未来城市发展[J].城市发展研究,2010(11).
