马尔可夫过程在银行信贷资金管理中的运用

2018-05-14王曦

财讯 2018年7期

关键词：信贷资金矩阵概率

王曦

信贷资金运行的过程中，由于各种因素使资金运行受阻，会造成逾期甚至不良资产。这给银行带来经营状况的恶化。在此将可吸收的马尔可夫链引入银行信贷资金管理中，在一步转移矩阵的基础上对信贷资产进行分析，对银行预防控制管理不良资产有一定的价值。

信贷资金

不良资产马尔可夫过程

贷款的分类

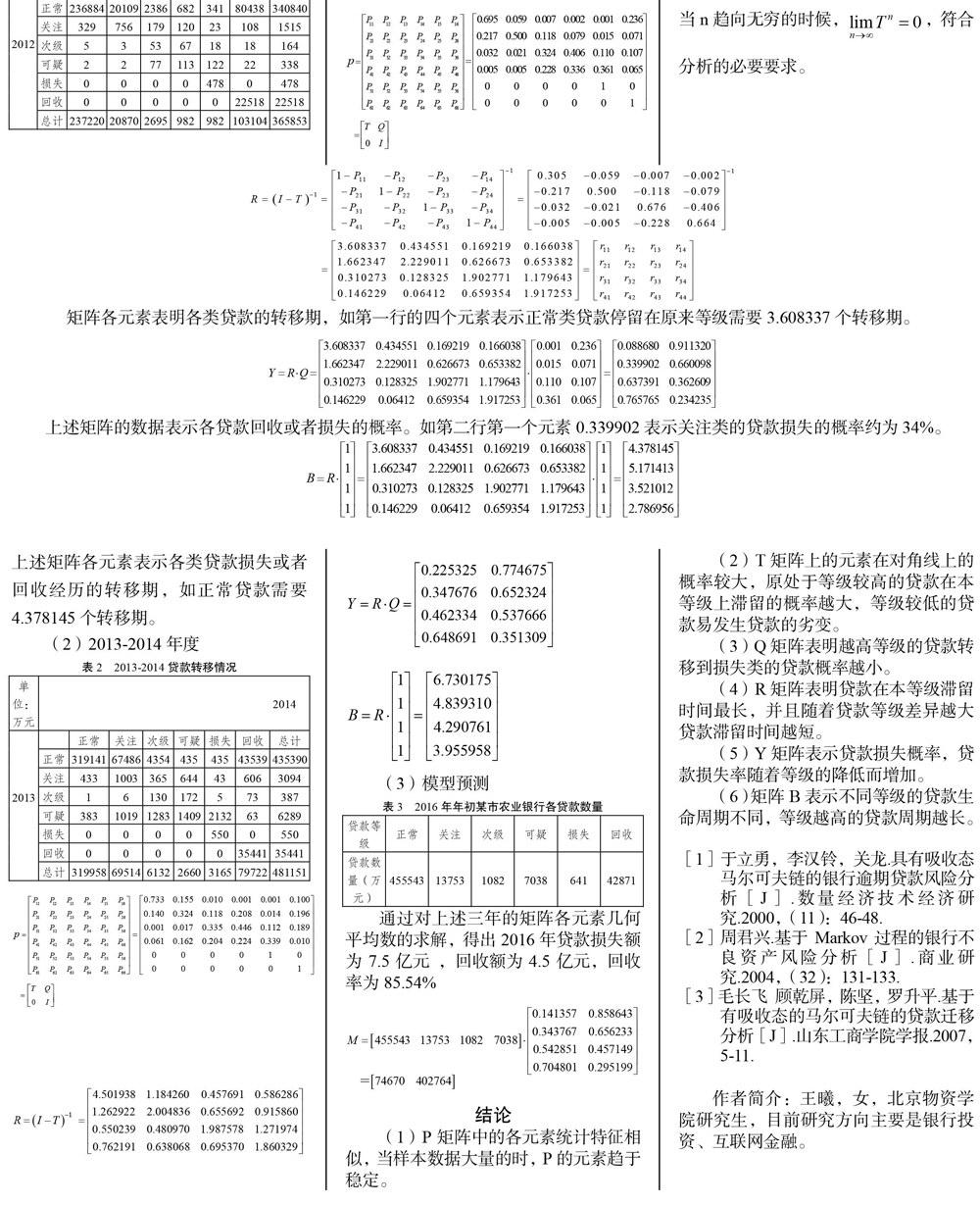
在我国，根据借款人的还款水平将贷款分为“正常、关注、次级、可疑、损失”五种类型，其中后三种为不良贷款。基于以上各贷款的特性，将其与已回收的贷款组成封闭集合N=（NI，N2，N3，N4，N5，N6），其中Nl至N6分别表示正常、关注、次级、可疑、损失、回收类贷款，N1，N2，N3，N4为暂态，N5，N6为吸收态，一旦进入吸收态，贷款损失或回收，该状态不可返回。将时间进行离散化处理，状态的时间间隔为一年，假设在年初贷款的状态是Ni，在年末的时候状态变为Nj，在j≠6下，i>j贷款的状况变好，i=j没发生变化，i

马尔可夫过程原理

设{X（t），t∈T}玛为一个随机过程，E为状态空间，对于任意n≥1 t1>t2>t3…tn∈T且x1 x2…xn已知X（t1）=x1X（t2）=x2…X（tn）=xn，条件下的条件分布函数只与X（tn）=xn有关，与前面各项无关，即

P（X（T）=x|X（tn）=xn，X（tn-1）=xn-1，…X（t1）=x1）=P（X（t）=x|X（tn）=xn）则{X（t），t∈T}稱为马尔可夫过程。

当马尔可夫过程参数集T和状态集X均为离散型时称其为马氏链，马氏链有两个性质：（1）无后效性：当tk已知时，t>tk的状态只会与tk状态有关而与之前状态无关。（2）平稳性：在k时刻状态i到k+1时刻状态j的一步转移概率为：P（xk+1=j|xk=i）=pij（k）=pij（1）（k）i，j=1，2，3…n若假定上式与“无关，即P（xk+1=j|xk=i）=…P（x1=j|x0=i）=pij则该马氏链具有平稳性。以上可以得到p（k）=p（k-1）·p=…=pk。

模型的建立与检验

（1）模型运用的依据

银行的年末贷款状况分布主要与年初贷款数量和结构有关，与过去年份贷款特征和分布呈现弱的相关性。同时贷款状态转移的概率是相对稳定的，因此贷款转移情况服从马氏链的原则。

（2）模型的建立

1.分块矩阵建立

基于马尔可夫链，建立贷款的一步转移矩阵。为了简化分析，不考虑年内的贷款增加数量。设状态集合S={N1，N2，N3，N4，NS，N6}其中N1，N2，N3，N4为暂态N5，N6是吸收态。

3.实证研究

以下是某市的农业银行分行的2012-2015三年的贷款转移各数量，进行分析：

（1）2012-2013年度上述矩阵各元素表示各类贷款损失或者回收经历的转移期，如正常贷款需要4.378145个转移期。

（2）2013-2014年度

（3）模型预测

通过对上述三年的矩阵各元素几何平均数的求解，得出2016年贷款损失额为7.5亿元，回收额为4.5亿元，回收率为85.54%