NaCl晶体马德隆常数的计算

何东山

（咸阳师范学院 物理与电子工程学院，陕西 咸阳 712000）

在固体物理学中，马德隆常数是描述晶体结构的一个重要特征参数，通过马德隆常数便可以计算出晶体的库仑结合能。NaCl晶体一个原包的平均库仑结合能可以表示为[1]

其中求和部分是取决于晶体结构的无量纲负值，将其记作-α，其中α被称作马德隆常数，其表达式为

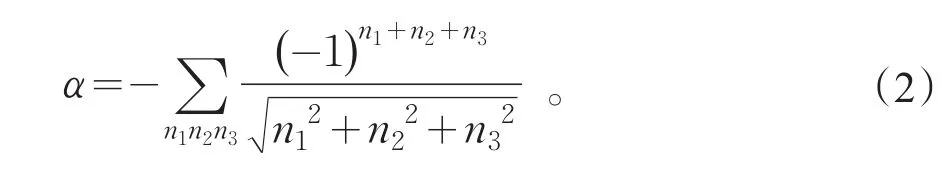
根据式(2)便可以计算出马德隆常数，但是对于三维情况，上述级数收敛很慢。本文通过对一维和二维NaCl晶体马德隆常数的计算分析，给出了减小计算量和加快收敛速度的方法，并计算了三维NaCl晶体的马德隆常数。

1 一维NaCl晶体马德隆常数的计算

1.1定义算法

一维NaCl晶体是指Na+离子和Cl-离子在一条直线上等间距排列，其马德隆常数为

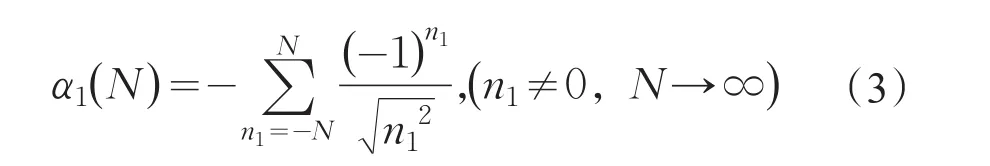
式（3）的严格结果为2ln2[2]，如图1所示，虚线表示α1随计算项数N增加时的变化规律，实线表示α1的准确值。根据式(3)，用Mathematica软件给出了α1(N )的图形，从图（1）中可以看出随着求和项数N增加时，α1在准确值上下摆动，且摆动幅度大致相同，项数N越大时摆动幅度越小，最终趋于准确值。

图1 定义法计算一维NaCl晶体马德隆常数

1.2改进算法

从图1中可以看出当项数N增加1时，结合能增加一个Na+离子或Cl-离子，因此马德隆常数在准确值两侧摆动，如果将公式修正为

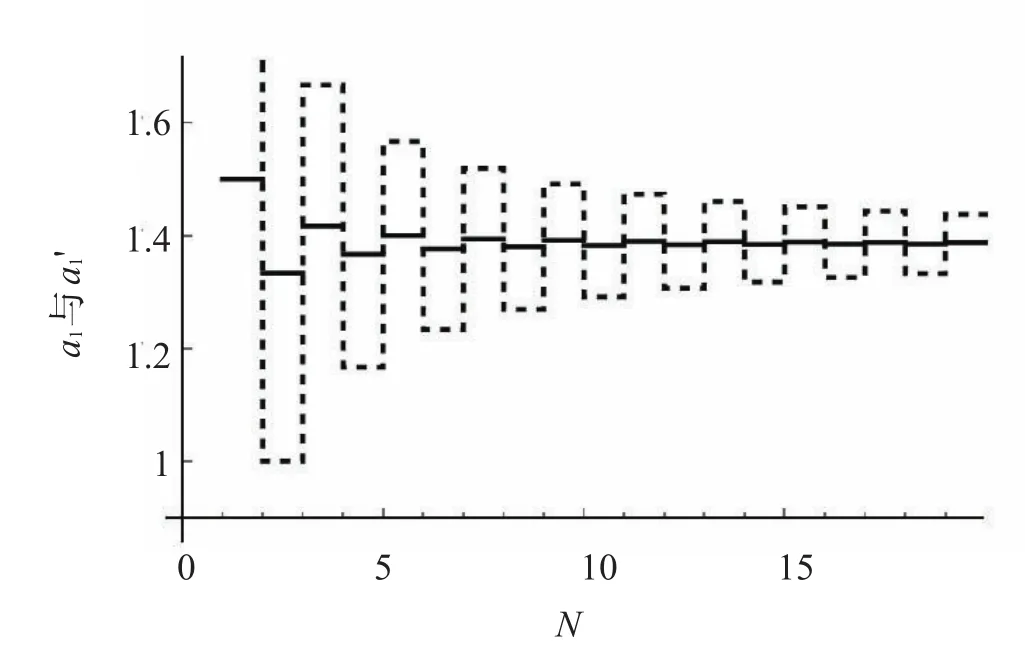
图2修正算法计算与定义算法对比

则收敛速度会大大加快。如图2所示，虚线表定义法得到的马德隆常数α1收敛情况，实线表示修正算法给出的马德隆常数α1'收敛情况。图中给出了修正算法计算与定义算法对比，可以看出修正算法的收敛速度远大于定义算法。根据对称性n取正值部分的求和与n取负值的求和部分相等，因此在式(4)中，将求和取为从1到N，将求和的计算量减小为式(3)的一半，这在一维情况下不是很明显，对于三维情况，可以减小很大计算量。

2 三维NaCl晶体马德隆常数的计算

根据定义二维NaCl晶体马德隆常数α2为

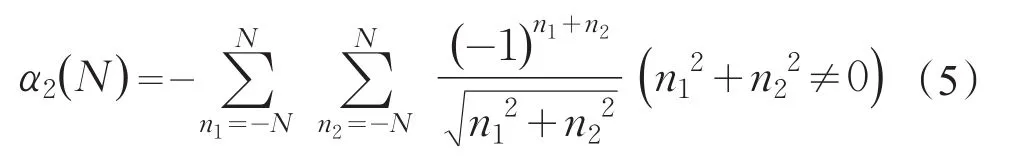
根据对称性，以参考离子为原点，则四个象限对原点的贡献相同，二维马德隆常数应为四个象限的贡献加上两个坐标轴上的贡献（即一维马德隆常数α1），因此式（5）可以重新写为

式(5)中求和为4N2项，而式(6)中求和约为N2项。根据定义三维NaCl晶体马德隆常数α3为

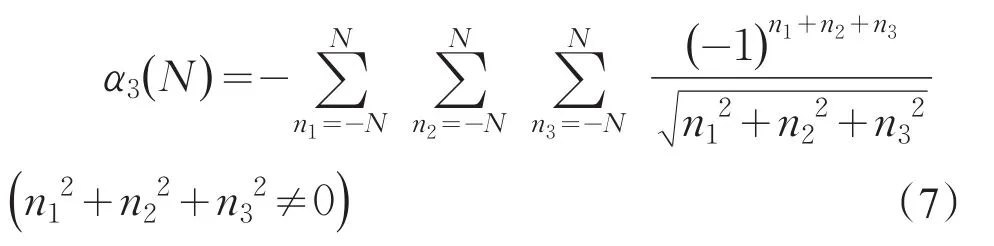
同理根据对称性将上式写为

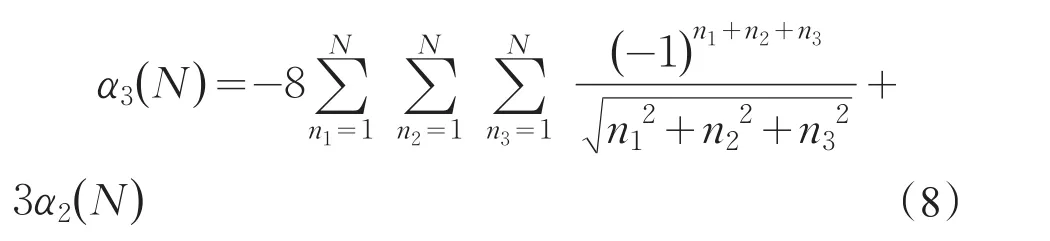
通过计算发现二维、三维马德隆常数与一维类似，随着项数的变化，其值在准确值两侧摆动，因此将公式修正为

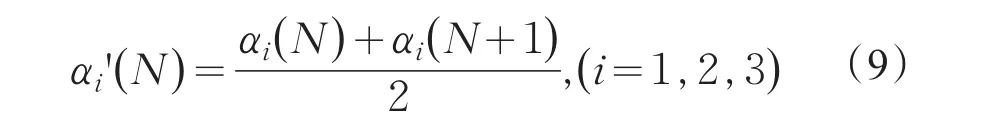
若利用式(7)和(9)计算三维马德隆常数则求和项共2×(2 N)2=16N3项，同理利用晶体的对称性可以将计算量减小在N很大时式(11)的求和项数约为N3项，相比定义法，式(11)大大减小了计算量，并加快了收敛速度。如图3所示，虚线表示定义法得到的三维马德隆常数a3，实线表示修正算法给出的三维马德隆常数a3'，修正算法更快的趋于稳定值，可见修正算法加快了计算的收敛速度。

图3修正算法计算与定义算法对比

3计算结果与分析

利用Mathematica软件，计算了一维至三维的马德隆常数，见表1。

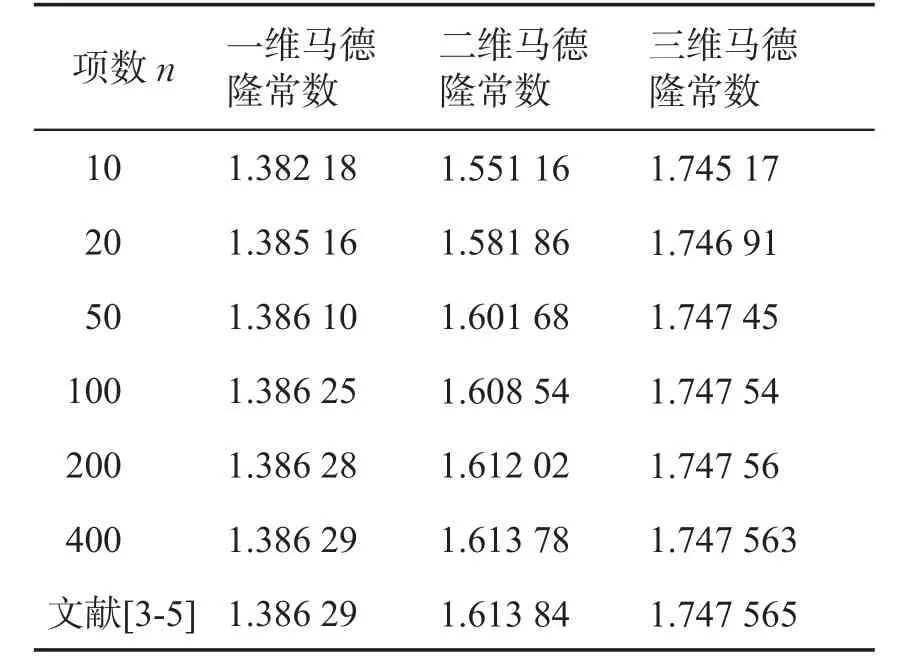
表1不同维度NaCl晶体马德龙常数计算结果

从计算结果可以看出，NaCl晶体各个维度的马德隆常数都随着项数n的增加而增加，项数n很大时马德隆常数增加的速度减慢，最终趋于一稳定值。项数n越大计算得到的精度越高，因此表1中当项数n增加到400时增加了结过的有效位数。但是计算过程中发现随着项数n的增加，计算机每次计算所花的时间迅速增加，为了节省计算时间，本文中计算到项数n=400为止。作为比较表1中列出了其他文献给出的各个维度的马德隆常数。可以发现本文计算结果与其他文献计算结果吻合。三个维度的比较表明，随着维数的增加马德隆常数也增加，这验证了离子晶体马德隆常数随着晶体配位数的增加而增大的性质[5-6],本文计算了简单晶的马德隆常数，对于复杂晶体通常计算方法更加复杂[7-10]。

参考文献：

[1]黄昆，韩汝琦.固体物理学[M].北京：高等教育出版社，1988.

[2]宋金璠，李书义.晶体马德隆常数的几种计算方法[J].南阳师范学院学报，2006，5（3）：32-34.

[3]刘策军.二维NaCl晶体马德隆常数计算[J].大学物理,1995，14（12）21-22.

[4]詹泸成，罗志琳.离子晶体的马德隆常数计算[EB/OL].北京：中国科技论文在线[2010-05-06].http：//www.paper.edu.cn/releasepaper/content/201005-161.

[5]王永杰，赵占龙.Nacl晶体的马德隆常数计算[J].保定学院学报，2007，20（4）：19-20.

[6]邱为钢.两维离子晶体的马德隆常数[J].大学物理，2016，35（4）：19-21.

[7]张维佳，王天民.复杂离子晶体马德隆常数研究[J].物理学报，2005，54（2）：565-573.

[8]田叶，侯春枝，杨兴强.NaCl晶体马德隆常数理论研究[J].南阳师范学院学报，2012，11（6）：29-33.

[9]唐芙蓉，杨先清，孙大鹏，等.菲波那契类准晶结构马德隆常数的研究[J].中国矿业大学学报，2007，36（5）：707-710.

[10]王矜奉，朱露莎，邓桂昌，等.采用双Evjen晶胞计算离子晶体的马德隆常数[J].四川师范大学学报（自然科学版），2001，24（5）：471-474.