考虑边界滑移和惯性效应的磁流变液缓冲器特性分析
2018-05-14王加刚余永刚廖昌荣叶宇浩
王加刚, 余永刚, 廖昌荣, 叶宇浩
(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.重庆望江工业有限公司,重庆 400071;3.重庆大学 光电工程学院,重庆 400044)
0 引言
传统的液压制退机是针对特定的冲击工况和预定规律进行设计的,其阻尼特性不可调,难以适应某埋头弹火炮的后坐要求[1]。利用磁流变液的可控流变特性,将磁流变液作为制退机的控制介质为可控制退机提供了崭新的思路。近年来,磁流变液应用于缓冲技术领域已得到国内外学者的关注:Ahmadian等[2]设计了双伸出杆的磁流变液阻尼器,冲击实验表明在活塞速度低于某特定速度时具有良好的可控性;Mikuowski等[3]针对飞机起落架的缓冲系统,设计了磁流变液自适应冲击缓冲器,实现了对冲击力的控制作用;Mao等[4]研制了多级通道串联的磁流变能量吸收器,建立了非线性模型并进行冲击测试;Bajkowski等[5]针对AKMS 7.62 mm小口径卡宾枪设计了磁流变制退机,完成了在单发射击条件下的高速冲击能量耗散评估;Singh等[6]针对最小后坐力传递和最快发生速度的问题,研究了磁流变应用于反后坐的优化控制方法;Bajkowski等[7]针对某武器系统,研究了基于复进弹簧与磁流变阻尼器反后坐装置的参数辨识,在600~650发/min射频条件下,取得了良好的控制效果;Ahmadian等[8]评估了磁流变技术应用于火炮反后坐领域的优缺点;张莉洁等[9-10]研究了磁流变液缓冲器的结构设计和动态特征,搭建了火炮冲击实验平台,评价了所设计缓冲器的实际效果;黄林等[11]针对在高冲击载荷下存在的流体通道堵塞等问题,设计了新型的磁流变液缓冲器;Ouyang等[12]针对长后坐行程制退机的要求,研究了四线圈励磁的磁流变阻尼器,取得了较理想的后坐力特性;胡红生等[13]以高冲击高速环境下的某口径火炮反后坐装置为研究对象, 研究了磁流变阻尼器对火炮后坐运动的控制作用。文献分析表明,在磁流变液缓冲装置的理论分析模型中,前人均未考虑磁流变液在阻尼通道内的流动惯性和边界滑移的影响,而上述影响是存在的。为此,本文从理论上深入分析磁流变液在阻尼通道中流动惯性和边界滑移对缓冲器阻尼力的影响,进一步完善磁流变液缓冲器设计方法,对推动缓冲器的设计具有重要的学术价值。
1 磁流变液缓冲器工作原理
根据火炮后坐过程的技术要求,相对运动部件分别作用于缓冲器的工作缸和活塞杆,拉伸过程要求具有可控的阻尼力,压缩过程具有较小的阻尼力。如图1所示,磁流变液缓冲器由工作缸、活塞组件、聚氨酯缓冲垫以及密封组件等组成。磁流变液充满缓冲器左、右工作腔,缸盖与缸体之间通过连接螺纹压缩紫铜密封圈实现密封,芯轴与缸体之间采用2个密封圈实现芯轴相对于缸体滑动的密封,活塞头中心线圈导线过孔间隙处利用环氧树脂胶进行封堵,从而保证了磁流变液在工作缸内的有效密封。工作腔两端设置聚氨酯缓冲垫,防止过量移动造成结构损坏。活塞头的外径与工作缸内径之间形成的间隙构成多级环形阻尼通道。在活塞组件上设置3组完全相同的螺旋管型励磁线圈,线圈之间的铜线通过串联连接,并通过活塞杆的中心通孔引出,阻尼通道中磁场方向(径向)垂直于磁流变液轴向流动,磁场的大小由通电线圈的励磁电流确定。在拉伸缓冲过程中,活塞杆受到冲击力相对于外筒向右运动,右腔中的磁流变液压力增大通过环形通道流入左腔,磁流变液在环形通道中的流动受外加电流产生的磁场控制,实现可控阻尼力。
2 缓冲器磁路有限元分析
磁流变液缓冲器采用剪切与流动混合模式,活塞头上的励磁线圈作为磁源,通过活塞头与工作缸形成闭合磁路。采用串级线圈励磁并优化其结构参数,增加了磁流变液磁控阻尼通道的长度;阻尼通道间隙两级励磁线圈反向绕制,使得两级线圈中间部分间隙的磁场叠加,避免两级线圈产生的磁场相互抵消,增加了阻尼通道的长度。在磁路设计时,要求能给阻尼通道提供足够的磁场。活塞头的铁芯采用电工纯铁,工作缸采用40CrMoA钢。磁流变液和铁芯材料的磁化参数由实验得到。对活塞头的磁路进行有限元分析,并反复修改磁路参数,得到优化后的结果如图2所示。分析结果表明,磁路各个部分均未饱和,阻尼通道的磁感应强度分布较为均匀,并且磁场不会泄露到外筒中,在活塞头和活塞套筒间形成了磁场回路,说明优化所得的磁路参数满足设计需要。
通过各自材料的磁化特性曲线可将磁感应强度代换为磁场强度,在单级匝数为180匝的情况下,计算得到励磁电流与通道平均磁感应强度,拟合结果为
B=0.690 3e0.013 5I-0.710 4e-0.802 4I,
(1)
式中:B为磁感应强度;I为线圈电流。
3 磁流变液本构模型及参数辨识
磁流变液是由高磁导率、低磁滞性的微小软磁性颗粒和非导磁性液体混合而成的悬浮液。在没有外加磁场条件下呈现出低黏度的牛顿流体特性;在外加磁场作用下,则呈现出高黏度、低流动性的滨汉流体特性。采用的磁流变液是重庆材料研究院有限公司提供的专用磁流变液(MRF-J25型,零磁场黏度为0.337 4 Pa·s)。在零磁场下的磁流变液本构特性可用牛顿流体模型描述:
(2)

在外加磁场作用下,磁流变液表现出滨汉流体特性,采用Herschel-Bulkley模型描述本构关系:
(3)
式中:τ0、k、n分别为Herschel-Bulkley模型中的参数;τy为磁流变液在流道y方向上所受的剪切应力。
采用安东帕流变仪对磁流变液特性进行测量,得到磁感应强度与模型参数之间的关系,结合(1)式,得到励磁电流与模型参数之间的关系式为
(4)
4 磁流变液在缓冲器通道中的流动特性
4.1 零磁场条件下磁流变液的流动
在零磁场情况下,由于环形通道宽度远小于活塞外径,利用平板模型进行分析建模,阻尼通道间隙为h(工作缸内半径与活塞头外半径之差),模型宽度为工作缸内周长与活塞头外部周长的平均值,如图3所示,其中v为磁流变液流动速度。分析其微单元受力,由牛顿运动定律得磁流变液流动微分方程,即Navier-Stokes方程:
(5)
式中:z为流道平行方向坐标;ρ为磁流变液的密度;u为磁流变液在通道内的流速分布;t为时间;p为通道产生的压降。假定沿流道长度方向压力梯度∂p/∂z是均匀的,压力梯度表达式简化为
(6)
式中:Δp为通道两端的压强差;l是通道长度。
(5)式右端项是流动的惯性项,采用平均惯性法可将(5)式变形为
(7)
平板模型下通道内体积流量Q计算为
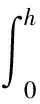
(8)
式中:R0为通道平均半径。体积流量相对于时间的导数为
(9)
将(9)式代入(7)式,结合磁流变液在零磁场下的本构模型(2)式,可得
(10)
将(10)式对y进行两次积分,得
(11)
式中:C1、C2为积分常数。考虑到磁流变液在阻尼通道壁面会存在滑移,采用Navier边界滑移条件:
vs=βτ,
(12)
式中:vs为边界处流体相对壁面流速;β为滑移系数。在(12)式的模型中,磁流变液的速度边界条件为
(13)
式中:v0为活塞头速度。
为了方便模型推导,作如下代换:
(14)
利用边界条件(13)式可解得
(15)
将(15)式代入(8)式进行积分,得流体流过通道时的体积流量为
(16)
设活塞和活塞杆的半径分别为Rh和Rr,则缓冲装置在缓冲过程时(活塞杆向外拉出)时,体积流量与活塞速度的关系为
(17)
将(16)式代入(17)式,再考虑(14)式,可得到活塞头两端的压力差与活塞运动速度、活塞加速度之间的关系。
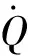
为分析流动惯性对于磁流变液流动速度的影响,取滑移系数β为0,通道两端压强差Δp=1 MPa,分别取流量导数为-0.5 m3/s2、0 m3/s2、0.5 m3/s2代入(15)式进行计算,通道内的流速分布如图5所示。当流量导数为正时,相比于匀速流动时其通道内流体的流速更小,反之当流量导数为负时,通道内的流速更大,可知当流速变化较大的条件下惯性项对于流动的影响比较大,在冲击缓冲这种流速变化较大的场合忽略惯性项会造成较大的误差。
4.2 磁场条件下磁流变液的流动
由Herschel-Bulkley模型可知,当剪切应力小于剪切屈服应力τ0时,磁流变液仅发生刚性流动,不发生剪切流动。当剪切应力大于剪切屈服应力τ0时,磁流变液发生剪切流动,其流速分布示意图如图6所示,图中区域Ⅰ和Ⅲ为剪切流动区域,区域Ⅱ为刚性流动区域。
由于(3)式所表示的Herschel-Bulkley本构模型在剪切速率分别为正和负时其表达式不相同,在所述的通道中一定会出现剪切速率随着y方向先正、后负的形态,首先对剪切速率为正的区域进行模型推导。
将(3)式中剪切速率为正的式子两边同时对y求导后得
(18)
将(18)式与(10)式一同代入(7)式,得到流速分布的微分方程:
(19)
对(19)式两边对y两次积分,并整理得
(20)
式中:C3、C4为积分常数。
令
(21)
考虑边界滑移,(21)式的边界条件与零场时类似,其中一个边界条件为u(0)=βτ. 假设y=y1处是其与刚性流动区域的分界处,由于流动流速梯度的连续性,另外一个边界条件为u′(y1)=0,磁流变液流速分布为
(22)
同理,对于剪切速率为负的区域,其流速分布为
(23)
由流速的连续性可得刚性流动区域的流速为
(24)
由于流道内流体的速度远大于活塞的运动速度,因此,通道内流体的流动可近似认为是一个对称的关系,通道中心流速最大,剪切应力应该为0,代入微分方程式解得
(25)
综上所述,刚性流动区域的分界点一定满足剪切应力正好等于磁流变液的剪切屈服应力±τ0,代入(25)式即可求得通道内刚性流动分界点的值:
(26)
由此,将(26)式代入流速分布表达式即得到整个流道流速分布,将流速分布函数代入(9)式即可得到流量、流量导数与通道两端压强差的关系式。由于磁流变液存在剪切屈服应力,当应力低于剪切屈服应力时,磁流变液不会发生剪切流动,因此对于整个通道而言,当作用在通道上的压强差小于某一特定值时,磁流变液同样不会发生流动。由(21)式可知随着压强差Δp的减小,其刚性流动区域的宽度也随之增大,当刚性流动区域的宽度大于通道本身宽度时,便代表着通道中不会发生流体流动,则此临界压强差Δp0为
(27)
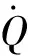
考虑了边界处的滑移,在相同的压强差下各个位置的流速都会增大,需要通过实验来确定边界滑移系数β的具体取值。
为了分析惯性项对磁流变流动速度的影响,取滑移系数β为0,同样取通道两端压强差Δp=50 MPa,分别取流量导数为-0.5 m3/s2、0 m3/s2、0.5 m3/s2代入模型(22)式~(24)式进行计算,通道内的流速分布如图8所示,可以观察到与零场时相同的结论。
4.3 磁流变液的阻尼力计算
由4.2节推导可知,整个活塞在运动时其受到的阻尼力主要由活塞头两端的压强差产生,通道节流产生的压降是活塞头速度与加速度的函数,小损耗因素压降是活塞头速度的函数。
在不考虑局部损耗条件下,由于整个活塞在缓冲过程时是工作在从活塞腔中拉出的状态,磁流变液缓冲器的阻尼力为
(28)
5 磁流变液缓冲器实验研究
根据第1节和第4节的分析计算,设计制作了磁流变液缓冲器,如图9所示。为了评价磁流变液缓冲器的缓冲性能,验证理论模型的正确性,设计了一套落锤冲击实验台架测试系统,如图10所示。冲击实验台架主要包括:落锤导向架、拉环、落锤、压板、冲击挡板、磁流变液缓冲器、压力传感器、激光位移传感器、位移探测板和缓冲器固定架。缓冲器固定架固定在地面上,压力传感器位于压力传感器压板与缓冲器固定架中间,被压力传感器压板与缓冲装置支架夹紧固定,缓冲装置活塞杆穿过压板和支架,缓冲装置外筒固定在压力传感器压板上。当活塞杆受冲击向下运动时,可以通过压力传感器测得缓冲装置外筒的受力情况。活塞杆通过一个拉力传感器连接在冲击挡板上,当冲击落锤作用在冲击挡板上时,挡板拉着拉力传感器与活塞杆一同向下运动,此时压力传感器即可测得冲击载荷的大小。激光位移传感器位于缓冲装置支架上,工作时其激光打在冲击挡板上,测量缓冲过程的位移变化规律。
完成不同冲击速度和不同励磁电流下的冲击实验,缓冲结果如图11所示,在相同的冲击速度下,对线圈施加不同的电流对缓冲装置缓冲力的影响较为明显。在冲击速度为1.55 m/s时,电流从0 A变化到3 A时,缓冲力逐渐增大。从缓冲力的峰值来看,电流从0 A到4 A,缓冲力增大了15 000 N,相对于电流为0 A时峰值增加了68.4%,电流为3 A和4 A的时候缓冲力波形非常接近,原因是当电流大于3 A后磁路出现了磁饱和现象导致可控性变差。在冲击速度为1.90 m/s时,电流从0 A到4 A,缓冲力增大了25 000 N,相对于电流为0 A时的峰值增加了105%,且同样出现了3 A和4 A的时候缓冲力波形接近的情况。
缓冲位移时间历程如图12所示,对于施加不同的电流,位移形态特征差别明显。随着电流的增大,缓冲的最大行程变小,其原因是由于电流越大缓冲力越大,使得缓冲过程更早的结束。在冲击速度为1.55 m/s时,电流为0 A时的最大位移比4 A时大6.6 mm,相对减少了42.5%;在冲击速度为1.90 m/s时,电流为0 A时的最大位移比2 A时大11 mm,相对减少了46.4%. 波形中出现的在位移达到最大值后的下降主要是由于较大冲击力使得冲击挡板变形后的回弹导致的。
为验证理论模型的准确性,将实际缓冲装置结构参数代入模型,采用迭代的思想完成对整个缓冲过程的仿真计算。利用计算机对冲击速度为1.55 m/s、1.90 m/s及电流为3 A时的情况进行仿真。由于冲击接触阶段(速度达到最大值之前)力学过程较为复杂,同时缓冲装置性能优劣主要体现在缓冲力峰值以及随后的变化规律,在仿真时假定其缓冲速度变化规律已知,峰值速度由动量守恒法则可得
(29)
式中:vmax为活塞的最大速度;M为落锤的质量;m为冲击挡板和活塞杆的质量;g为重力加速度;H为落锤冲击高度。
取不同的滑移系数β完成缓冲过程的仿真,仿真结果与实验对比图如图13所示。由图13可以看出:不考虑边界滑移时(β=0)仿真结果的缓冲力峰值明显高于实际的测量值,存在着较大的误差。而考虑边界滑移的情况时,仿真结果的缓冲力有明显的降低,当边界滑移系数取0.000 1的时候,可以观察到,仿真曲线与实际曲线吻合较好,能够较好地描述缓冲装置的实际特征。存在一定误差的原因主要有以下几点:忽略了落锤与导轨之间的摩擦力,冲击速度不准确;两个缓冲装置力学特征不完全相同;活塞与外筒在冲击时不同轴,导致活塞与外筒发生摩擦。总体来说,所建立的模型能够较好地反映缓冲装置的实际性能。
6 结论
本文建立了环形通道节流型磁流变液缓冲器的流动分析模型,设计制作了磁流变液缓冲器,搭建了冲击实验系统,开展了落锤冲击实验,比较了实验数据与理论预测,得出如下结论:
1)设计的多级环形通道的磁流变液缓冲器缓冲力、缓冲位移能随励磁电流发生变化,缓冲器的缓冲力是可控的。
2)建立的模型能够较好地描述该缓冲装置的特征,流动模型中加入的惯性项以及边界滑移完善了理论计算模型。
3)理论模型计算得出的缓冲力与实验结果变化趋势相符,其误差主要由冲击实验架的摩擦、冲击实验系统不稳定、缓冲装置活塞与外筒不同轴等因素造成。
参考文献(References)
[1] Wu Y C, Chang H, Tsung T T. Dynamic characteristics of a recoil system when firing projectiles with Mach 4.4 muzzle velocity from a 105 mm cannon[J]. Journal of Testing and Evaluation, 2010, 39(4): 509-513.
[2] Ahmadian M, Norris J A. Rheological controllability of double-ended MR dampers subjected to impact loading[C]∥Proceedings of Smart Structures and Materials 2004: Damping and Isolation. San Diego, CA, US: SPIE, 2004, 5386: 185-194.
[4] Mao M, Hu W, Wereley N M, et al. A nonlinear analytical model for magnetorheological energy absorbers under impact conditions[C]∥Proceedings of ASME 2009 Conference on Smart Materials, Adaptive Structures and Intelligent Systems. Oxnard, CA, US: ASME, 2009:393-404.
[5] Bajkowski M, Bajkowski J M. Design of the magnetorheological damper for the recoil damping of the special object 7.62 mm calibre[J]. Machine Dynamics Research, 2012, 36(1): 15-23.
[6] Singh H J, Wereley N M. Optimal control of gun recoil in direct fire using magnetorheological absorbers[J]. Smart Materials and Structures, 2014, 23(5): 055009.
[7] Makuch A, Bajkowski M, Lindemann Z. Determining parameters of recoil reduction system with spring and magnetorheological damper intended for special object[J]. Machine Dynamics Research, 2014,38(3): 87-96.
[8] Ahmadian M, Poynor J C. An evaluation of magneto rheological dampers for controlling gun recoil dynamics[J]. Shock and Vibration, 2001, 8(3/4): 147-155.
[9] 张莉洁, 王炅, 钱林方. 冲击载荷下磁流变阻尼器动态特性分析及模型参数辨识[J]. 机械工程学报, 2009, 45(1): 211-217.
ZHANG Li-jie, WANG Jiong, QIAN Lin-fang. Dynamic perfor-mance analysis and model parameter identifications of MR dampers under impact loads[J]. Journal of Mechanical Engineering, 2009, 45(1): 211-217. (in Chinese)
[10] 张莉洁, 王炅, 钱林方. 冲击载荷下磁流变阻尼器动态特性试验分析[J]. 兵工学报, 2008, 29(5): 532-536.
ZHANG Li-jie, WANG Jiong, QIAN Lin-fang. Experimental analysis of the dynamic performance of magneto-rheological dam-pers under impact loads[J]. Acta Armamentrii, 2008, 29(5): 532-536.(in Chinese)
[11] 黄林, 黄学功, 王炅. 新型磁流变阻尼器抗冲击载荷性能分析[J]. 机械设计与制造, 2012 (12):71-73.
HUANG Lin, HUANG Xue-gong, WANG Jiong. Anti-impact-load performance analysis of new MR damper[J]. Machinery Design & Manufacture, 2012 (12):71-73.(in Chinese)
[12] Ouyang Q, Zheng J, Li Z, et al. Controllability analysis and testing of a novel magnetorheological absorber for field gun recoil mitigation[J]. Smart Materials and Structures, 2016, 25(11): 115041.
[13] 胡红生, 王炅, 蒋学争, 等. 火炮磁流变后坐阻尼器的设计与可控性分析[J]. 振动与冲击, 2010, 29(2): 184-188.
HU Hong-sheng, WANG Jiong, JIANG Xue-zheng, et al. Design and controllability analysis of a gun magnetorheological recoil damper[J]. Journal of Vibration and Shock, 2010, 29(2): 184-188.(in Chinese)
