考虑最大暴露值的无线传感器网络最小暴露路径优化算法

杨廷鸿，方海洋，姜大立，方玲

(1.陆军勤务学院 军事物流系, 重庆 401331; 2.陆军勤务学院 基础部, 重庆 401331)

0 引言

作为一类分布式网络，无线传感器网络(WSN)具有可大规模部署、扩展性强、能耗较低、价格低廉等特点[1-2]，能对环境信息进行实时采集、处理和传输[3-5]。WSN现有的研究成果已被广泛应用于环境监测[6]、军事侦察[7]、智慧城市建设等多个领域[8]。

最小暴露路径(MEP)是用来衡量WSN覆盖效果[9-13]的重要方法，其优化问题一直是广大学者密切关注的热点问题。一般来说，该类问题可归结为曲线积分优化问题[14-15]，其数值解法主要有两种：基于Voronoi图的方法和网格划分的方法。Voronoi图方法最早在文献[16]中提出，该方法根据监测区域内传感器的几何位置来构建Voronoi图，然后计算每条边的暴露值，并通过最短路径算法求解出MEP. 在此基础上，其他文献又提出了很多改进的方法：Djidjev[17]整合Voronoi图和欧拉- 拉格朗日方程寻找MEP；Zhang等[18]在解决MEP问题过程中以Voronoi图为基础，提出了分布式路径搜索方法；文献[19]则利用Voronoi图和Dijkstra算法(DA)搜索传感器网络中易受攻击的路径。对于网格划分的方法而言，它首先将监测区域划分成正方形的网格，并限制目标只能在网格的边或者对角线上移动，然后再找出MEP[20]. Liu等[21]利用该方法研究了有向传感器网络中的MEP问题；文献[22]提出了基于渗流的方案，将MEP问题转化到三维均匀网格中，再利用网格划分的方法求解；针对区域限制下的MEP问题，Feng等[23]将路径分成3段，其中第2段需要穿过限制区域，第1段和第3段使用网格划分的方法求解，第2段使用混合遗传算法来求解。针对不同的研究背景，很多其他的基于网格划分的改进方法也被相继提出。然而，基于Voronoi图的方法对传感器数量以及传感器有无方向性具有很大限制，网格划分的方法虽然能克服上述不足，但其计算复杂度对网格规模非常敏感。

事实上，在一些重点监测或防御区域，传感器部署的密度相对较高。例如在军事上，交战双方会在重要的关口、要塞、道路上设置大量的各类型监控传感器，对敌方入侵进行密切监控；在珍稀动物保护区，为了监测珍稀动物的生活习惯，会在保护区内部署大量的摄像头或红外探测仪以进行实时监测。同时，当网格规模越大，分辨率越高，离散化带来的模型误差越小。因此，网格规模大、传感器密度高的WSN中MEP优化问题引起了学者的关注。

针对网格规模大、传感器高密度的MEP优化问题，一些学者提出利用启发式算法来降低算法的复杂度，如文献[24]提出了多头绒孢菌优化算法，利用多头绒孢菌的避光性来解决这一问题。但当网格规模或传感器密度改变时，这一算法中的参数需要重新调整，算法的普适性不够强。文献[25]中，在考虑目标导向的情况下，以随机漫步算法和DA为基础，提出了导向相遇随机漫步算法(TGSARWI DA)。该算法能获得与DA暴露度高度一致的路径，且很大程度上克服了计算复杂度对网格规模和传感器密度的敏感性。不过上述算法只关注路径的暴露度之和，而忽略了路径上局部路段(边)的最大暴露值。根据木桶短板原理，暴露值最大的边往往在很大程度上决定了WSN覆盖质量的好坏。例如，在WSN应用的某些特殊领域(诸如军事上的穿越战场、城市安防建设等问题)，通常涉及到在通往重要目标的关键区域部署更多的传感器来加强对外来目标的监测问题。虽然经过该区域的路径能保证暴露度之和最小，但路径上的最大暴露值相对较高，反而更容易暴露目标。文献[26]考虑了路径长度的影响，但是网格化的WSN是典型的加权网络，直接用路径的长度显得不够合理。

本文首先简述了基于网格划分的WSN中MEP优化问题；随后在考虑路径中最大暴露值影响的情况下对经典的DA进行改进，形成考虑最大暴露值的DA(DAME)，并在此基础上结合TGSARWI算法提出了解决网格大规模、传感器高密度WSN中MEP优化问题的TGSARWI DAME；最后从参数分析、算法性能评估以及实例验证3个方面对算法进行了仿真和分析。

1 基于网格划分的WSN的MEP优化问题

设N个传感器{S1,…,Si,…,SN}部署在某一网格划分的区域，WSN中的MEP优化问题是指在该区域中，找到一条MEP连接源节点vs和目标节点ve，其中s和e分别表示源头和目标。

1.1 暴露度定义

假设目标在传感器监测下的暴露强度和它们之间的距离呈反比，即目标距离传感器越远，目标的暴露度越小。根据文献[24]，定义距离传感器Si为d的目标O在其监测下的暴露度为

(1)

式中：μ和τ为传感器的性能参数，根据文献[26]，可取值为1.

如果传感器的探测具有方向性，则目标被传感器监测的暴露度还与方向角有关。一般地，偏离传感器中心方向的角度越大，暴露度越低。因此，对于方向型传感器，定义目标在传感器下的暴露度为

(2)

式中：Vi表示有向传感器探测的中心方向向量；SiO表示传感器Si和目标O的方向向量；φ(A,B)表示A、B两向量间的夹角；γ为传感器的性能参数，根据文献[27]，可取值为1.

根据上述定义，在部署有N个传感器的区域内，目标被监测的暴露度有两种表示方法[24]：一是将目标在所有单个传感器下的暴露度相加，即

(3)

二是取被监测暴露度的最大值，即

(4)

由(1)式和(2)式可知，虽然区域内任意位置目标在所有传感器的监测下均具有一定的暴露度，但是根据文献[28]，该暴露度随目标与它们之间距离以及偏离有向传感器中心方向角度的增大而急剧衰减。因此，在目标被多个传感器监测暴露度的计算中，往往由监测效果最佳的一个或者少数几个传感器起决定作用。另一方面从计算复杂度的角度考虑，(4)式的计算复杂度远远小于(3)式，尤其是在传感器大量部署的情况下这一差异更为显著。因此，依据文献[24]，本文采用第2种方式。

1.2 网格划分区域

网格划分区域的基本思想是将无线传感器监测区域划分为m×n的网格，假设目标只能沿着网格的边进行移动。

一般可以用无向图G=(V,E,W)表示网格型网络，其中V为所有网格节点的集合，E为所有网格边的集合，W为边的权重(网格边的暴露度)的集合。参照文献[24]，若记网格边的长度为l，编号i的节点记为vi，其坐标记为(xi,yi)，网格网络中相邻两个节点vi、vj之间边的权重wij表示为

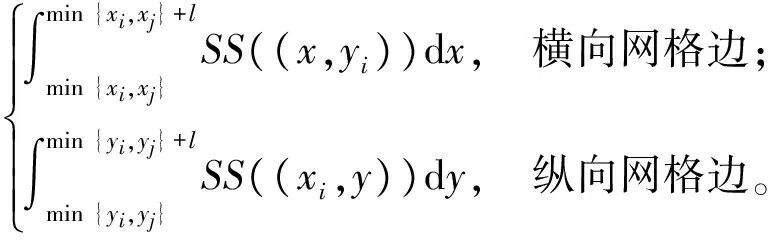
(5)

2 考虑最大暴露值的WSN中MEP优化问题求解算法

2.1 考虑最大暴露值的优化目标

一般地，如果不考虑路径上的最大暴露值，路径H={vt1,vt2,…,vtp}上的暴露度等于路径H上各路段暴露值之和，即

(6)

vt1，vt2，…，vtp表示路径H上的p个节点，t1，t2，…，tp表示路径H上节点对应于网格网络中的节点编号。经典的DA寻求源点至网络中其他各节点的最短路，就是以E(1)(H)最小为目标进行的。

若要考虑路径上边的最大暴露值，可以改进(6)式，定义路径H的暴露度为

(7)

式中：α为权重，0<α<1.

对于短路径而言，其暴露度总和与最大暴露值之间的数量级差异不明显，但对于长路径而言，两者差异可能较大，这可能导致最大暴露值无法发挥其作用。因此，(7)式中参数的选取难以兼顾不同路径长度。

考虑到DA求解最短路径的过程是借助已知的最短路像滚雪球一样一层一层地扩展出新的最短路径。每一次探寻新的最短路其实就是尝试将已知最短路再延伸一段，即新的最短路只会由某条已知的最短路增加一条边构成。受到该算法的启发，给出具有递推关系的衡量路径暴露程度的指标为

E(3)(H{vtp′})=

(8)

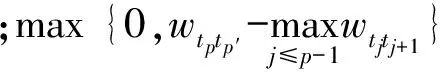
事实上，(8)式中罚因子β的作用依然受到网格规模和路径长度的影响。但是，可以通过两阶段运行本算法来克服：第1阶段运行以(8)式目标寻找临时MEP，并记该路径的最大暴露值为epmax；第2阶段运行以(9)式为目标寻找MEP. 只要β足够大，就能有效回避路径最大暴露值的增加。

E(3)(H{vtp′})=

(9)

因此，若将经典DA的优化目标由E(1)(H)改为E(3)(H)，则可以将路径上的最大暴露值纳入MEP问题的求解之中，形成DAME.

2.2 DAME的构建

为了便于算法的描述，记E(3)(v)为源点vs到节点v的MEP考虑最大暴露值的路径暴露度；maxEP(v)为源点vs到节点v的MEP最大暴露值。

由于DAME更改了DA的优化目标，相应的算法步骤内容也应作相应改进，其流程图如图1所示，其中Γ(v)记录节点v到源节点vs最短路径的父节点信息。

在无向图G=(V,E,W)中的DAME具体描述如下(其中k表示算法运行阶段：0表示第1阶段，1表示第2阶段)：

1)初始化k=0，为源节点vs标号P，并令E(3)(vs)=0，maxEP(vs)=0；其余节点标号T，记Δ={vj|vj∈V&vj≠vs}，有∀vj∈Δ，T(vj)=∞；

2)遍历vj∈Δ&(vs,vj)∈E，令T(vj)=wsj，Γ(vj)=vs，转步骤4；

3)针对所有vt∈R，遍历vj∈Δ&(vt,vj)∈E，若T(vj)>E(3)(vt)+wtj+βmax {0,wtj-maxEP(vt)}，则令T(vj)=E(3)(vt)+wtj+βmax {0,wtj-maxEP(vt)}，Γ(vj)=vt；

4)令R=∅；

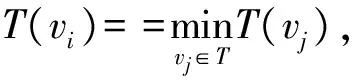
6)若k=0，则转步骤7，否则算法结束；

7)记epmax=maxEP(ve)，并重置各参数：k=1,为源节点vs标号P，并令E(3)(vs)=0，maxEP(vs)=epmax，其余节点标号T，记Δ={vj|vj∈V&vj≠vs}，有∀vj∈Δ，T(vj)=∞，转步骤2.

上述算法中，Γ记录的源节点vs到其他各点的最短路径信息并不完全，但一定包含了源节点vs到目标节点ve的最短路径Hmin的完整信息。Hmin可以通过以下回溯算法求解：

1)初始化Hmin={Γ(ve),ve}，令vt=Γ(ve)；

2)若vt=vs则回溯结束，否则转步骤3；

3)令Hmin={Γ(vt)}Hmin、vt=Γ(vt)，转步骤2.

2.3 TGSARWI DAME的构建

TGSARWI算法主要通过模拟多个探路者在陌生区域的探路过程寻找连通源节点和目标节点的连通子网络[25]，其核心思想是通过建立通路子网络以降低网格规模。

若某一探路者t时刻由路径Ht到达节点vt，位置坐标为(xt,yt)，则其目的地(源节点或者目标节点)为v*，位置坐标为(x*,y*)。探路者在网格上进行随机移动，他从当前节点vt移动到下一个节点vj的转移概率为

(10)

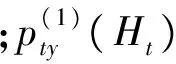
(11)

利用该转移概率可以排除已经走过的节点，提升探路效率，但也有可能造成探路者被密集的传感器“堵死”或者被自己前面经过的路径“围死”而无路可走。因此，在随机游走过程中必须设置游走的局部回溯功能以及重启功能。

由于单条路径具有一定的随机性，从源节点和目标节点同时派出nf个探路者进行探路，直到形成nh条通路为止，再将这些通路组合成一个连通的子网络G1=(V1,E1,W1)。此时，子网络G1的规模远远小于原网络G.

将TGSARWI算法与本文提出的DAME相结合，构建TGSARWI DAME，算法的基本思想是：首先，利用TGSARWI算法构建通路子网络；然后，利用DAME在通路子网络中寻找考虑最大暴露值的MEP.

DAME是在DA的基础上更改了生成新的最短路的标准以及记录相应最短路的父节点，其复杂度与DA相当。因此，TGSARWI DAME与TGSARWI DA的复杂度也是相当的。文献[25]的研究表明，TGSARWI DA的复杂度甚至不足DA的1‰，这充分表明了TGSARWI DAME也具备求解网格规模大、传感器密度高的MEP优化问题的能力。

3 算法仿真与结果分析

3.1 参数分析

假设某50×50的网格区域部署了50个传感器，网格长度l=10 m，传感器密度为0.02，有向传感器和无向传感器是混合随机分布的。根据文献[28]，取导向调节因子ρ=0.9，罚因子β在区间[10-2,106]之间取值，分别探寻最佳路径H，并计算其暴露度总和E(1)(H)和最大暴露值maxEP(H)。

由于传感器类型及分布是随机的，为了克服样本随机性带来的影响，对于每一个β值均随机生成50组传感器类型及分布，并计算相应的E(1)(H)和maxEP，然后取其平均值作为该β值下的相应指标。图2给出了路径H的暴露度总和E(1)(H)和最大暴露值maxEP(H)随着罚因子β的变化曲线图。

由图2可以发现，当β<1时，E(1)(H)和maxEP(H)几乎没有变化，说明较小的β值很难对算法求解产生影响。当β>1时，maxEP(H)呈现出快速下降趋势，并在β>100之后再次呈现出稳定趋势，而在相应的阶段中E(1)(H)一直呈现明显的上升趋势，直至β>1 000后呈现平稳态势。因此，可以认为β=100为最佳取值。

另外，当取其他网格规模和传感器密度时，E(1)(H)和maxEP(H)的变化趋势和上述仿真一致。这一结果说明TGSARWI DAME具有很好的普适性，一旦罚因子值确定后，在不同的传感器网络背景下均无需再分析其最佳取值。因此，后续分析直接将算法中的罚因子取值为100.

3.2 对比分析

3.2.1 TGSARWI DAME与TGSARWI DA对比分析

设HTDAME、HTDA分别表示TGSARWI DAME、TGSARWI DA得到的最佳路径。为对比分析两种算法，定义路径HTDAME相对于路径HTDA关于暴露度总和E(1)的亏损率为

(12)

关于最大暴露值maxEP的收益率为

(13)

同时，定义收益亏损比为

(14)

η类似于经济中的投入产出比：若η>1，则说明牺牲较小的路径暴露度获得了较大的最大暴露度改进，此时算法有效；反之亦然。

3.2.1.1 网格规模的影响

假设传感器的密度为0.02，传感器类型(含方向)和位置都是随机生成的(下文也进行相应的设定)，网格规模从10×10到700×700进行变化。考虑到传感器的随机性，仿真时对于每一个网格规模都进行30次重复仿真，分别取暴露度E(1)和最大暴露值maxEP的平均值，在此基础上计算亏损率和收益率。

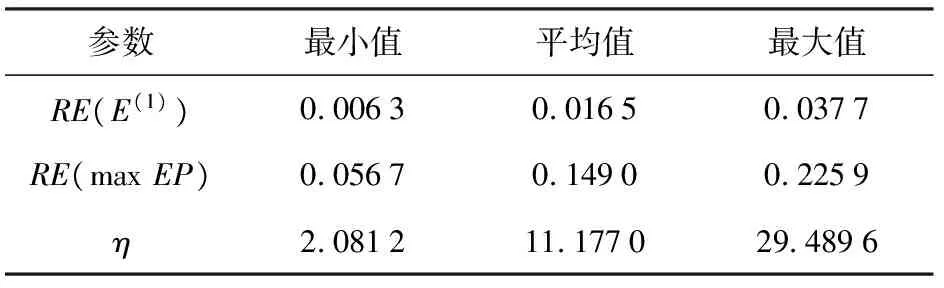
图3给出了不同网格规模下路径HTDAME和HTDA暴露度的对比趋势图以及它们的相对误差和收益率的变化图。通过图3(a)和3(b)可以看出：两条路径的暴露值几乎重合，都呈现出上升趋势；最大暴露值也都呈现出增加趋势，但是后者的最大暴露值都大于前者，并且相对差值越来越显著。从图3(c)中可知，最大暴露值的收益率要远远高于路径暴露度的亏损率。表1给出了不同网格规模下路径暴露度总和与最大暴露值的亏损率、收益率以及收益亏损比的信息。从图3(d)和表1可以看出，该方法下的最大收益比为29.49，平均值为11.18，均远大于1.

表1 不同网格规模下路径暴露度总和与最大暴露值的亏损率、收益率以及收益亏损比的信息
Tab.1 Loss rate of path exposure, profit rate of maximum exposure, and ratio of profit rate to loss rate under the condition of various grid scales

参数最小值平均值最大值RE(E(1))0 00630 01650 0377RE(maxEP)0 05670 14900 2259η2 081211 177029 4896

3.2.1.2 传感器密度的影响

固定网格规模为50×50，传感器密度从0.4%～40.0%之间进行变化。与网格规模变化类似，同样比较TGSARWI DAME与TGSARWI DA之间的路径暴露度总和与最大暴露值的变化趋势，并计算亏损率和收益率等。

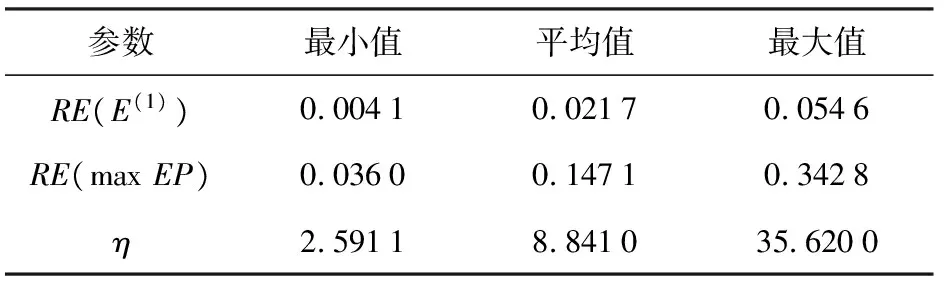
图4和表2分别给出了不同传感器密度下，路径HTDAME和HTDA的暴露度总和与最大暴露值对比趋势图、它们的相对误差和收益率变化图以及相应的量化分析结果。从图4(a)中可以发现，两种算法得到的路径暴露度几乎重合，均随传感器密度增加而呈现出上升的趋势。这说明不同传感器密度下，TGSARWI DAME保持了TGSARWI DA探寻MEP的特征。从图4(b)可以看出，路径HTDAME最大暴露值明显小于HTDA的 最大暴露值，且当传感器密度达到一定值(约0.12)时，前者的最大暴露值几乎稳定，而后者依然在显著上升。一方面，充分体现了在不同传感器密度下，TGSARWI DAME回避最大暴露值的优异性能；另一方面，从传感器网络覆盖的角度而言，单纯依靠增加传感器密度来提高覆盖质量，在密度达到一定的临界值后，其效果将微乎其微。图4(c)中给出了不同传感器密度下TGSARWI DAME的亏损率和收益率的变化曲线。亏损率始终在接近于0的附近波动，而收益率则远大于亏损率，其呈现出明显的上升趋势。从图4(d)和表2看出，亏损收益比平均值大约为8.84，最大值达到35.62，它们同样远大于1.

以上结论充分说明了TGSARWI DAME能够适应大规模网格和高密度传感器下的MEP优化问题求解，并且能通过损失较小的路径暴露度(平均上升小于2.2%)来显著改善路径上的最大暴露值(平均降低约15%)。这使得该方法可以在很多传感器网络的应用上发挥重要作用，如军事上的穿越战场监控区域问题。

表2 不同传感器密度下路径暴露度和最大暴露值的亏损率、收益率以及收益比的信息
Tab.2 Loss rate of path exposure, profit rate of maximum exposure, and ratio of profit rate to loss rate under the condition of various sensor densities

参数最小值平均值最大值RE(E(1))0 00410 02170 0546RE(maxEP)0 03600 14710 3428η2 59118 841035 6200

3.2.2 TGSARWI DAME与DA对比分析

DA是求解网格化MEP问题的最优算法，下面将对比TGSARWI DAME与DA以分析前者求解MEP问题的性能。为了便于后文描述，记HDA为由DA在全局网格上寻求的MEP路径。由于DA的计算复杂度为O(m2n2)，相对较高，限制了仿真比较的网格规模范围。因此，在仿真过程中，仅让网格规模从10×10到150×150进行变化，其他仿真条件及研究方法与3.2.1节相同。

图5给出了由TGSARWI DAME和DA得到的路径暴露度总和与最大暴露值在不同网格规模以及不同传感器密度下的变化曲线。由图5(a)和图5(b)可知，在网格规模较小时，两种算法得到的路径暴露度总和与最大暴露值都基本重合。当网格规模进一步增大时，尽管由TGSARWI DAME得到的路径暴露度总和略微高于DA，但路径上的最大暴露度明显低于DA，这一趋势随着网格规模的增加会更加显著。由图5(c)和图5(d)可知，二者得到的路径在不同传感器密度下的路径暴露度总和基本一致，但当传感器密度增加到一定程度时，TGSARWI DAME得到的最大暴露值基本稳定到某一固定值，DA得到的路径上最大暴露值则处于继续增长的趋势，这充分说明TGSARWI DAME降低路径上最大暴露度的优势是非常明显的。

3.3 实例验证

实例1假定WSN的网络与3.1节相同，β=100，分别利用TGSARWI DAME和TGSARWI DA寻找MEP.

图6中分别给出了TGSARWI DAME和TGSARWI DA得到的MEP比较图。从图6中可以看出，TGSARWI DAME找到的MEP(红色)能够很好地避开暴露值较大的区域，与TGSARWI DA相比较而言，虽然前者的E(1)与后者基本一致，但实现了将maxEP降为后者约一半的目标。

实例2设定网格规模为700×700，传感器密度为0.02，即传感器的数量约为9 800个。源点和目标点的坐标分别为(1 120 m, 6 160 m)和(5 880 m, 1 680 m)。

这里，分别利用TGSARWI DAME、TGSARWI DA找出MEP. 图7和图8分别给出了计算结果的全局图和局部图。

从图7中可以看出，整个网格区域规模非常大，且传感器密密麻麻，基本上无法正常判断出MEP. 但是算法依然给出了相应的路径。从图8中可以发现TGSARWI DA为了寻求路径暴露度的最小化，强行通过暴露度较大的路段。而TGSARWI DAME虽然相对于TGSARWI DA损失0.786 0的路径暴露度，但能使得整条路径上最大暴露值降低0.328 51.

现有的MEP问题求解算法中，最大的计算网格规模为150×150，实例2的网格规模远远超过该规模。3.2节中对比分析涉及的网格规模和传感器密度以及实例2的解决充分说明了TGSARWI DAME具备求解大规模网格和高密度传感器背景下的WSN中考虑最大暴露值MEP优化问题的能力。

4 结论

本文将路径最大暴露值的有效控制纳入MEP问题的求解，提出了TGSARWI DAME，经过与传统算法仿真进行对比，得出以下结论：

1)该算法能够有效规避MEP中暴露值较大路段，在不同网格尺度、不同传感器密度下，最大暴露值平均降低14.7%.

2)路径暴露度能够保持与DA、TGSARWI DA相当的精度，在不同网格尺度、不同传感器密度下，路径暴露度平均偏差不超过2.2%.

总体而言，本算法能够求解网格大尺度、传感器高密度与考虑最大暴露值的MEP问题，适用于战场监控区域的穿越等问题。

参考文献(References)

[1] Shahid N, Naqvi I H, Qaisar S B. Characteristics and classification of outlier detection techniques for wireless sensor networks in harsh environments: a survey[J]. Artificial Intelligence Review, 2015, 43(2): 193-228.

[2] Mahmood M A, Seah W K G, Welch I. Reliability in wireless sensor networks: a survey and challenges ahead[J]. Computer Networks, 2015, 79(1):166-187.

[3] Lewis F L. Wireless sensor networks[M]∥Cook D J, Das S K. Smart Environments: Technologies, Protocols, and Applications. Hoboken, NJ, US:Wiley-Interscience, 2005: 11-46.

[4] Iyengar S S, Brooks R R. Distributed sensor networks: sensor networking and applications[M]. Boca Raton, FL, US: CRC Press, 2016: 35-56.

[5] Khan S, Pathan A S K, Alrajeh N A. Wireless sensor networks: current status and future trends[C] ∥ Proceedings of 2012 IEEE Symposium on Computer Applications and Industrial Electronics. Boca Raton, FL, US:IEEE, 2012: 267-272.

[6] Srbinovska M, Gavrovski C, Dimcev V. Environmental parameters monitoring in precision agriculture using wireless sensor networks[J]. Journal of Cleaner Production, 2015, 88: 297-307.

[7] Ball M G, Qela B, Wesolkowski S. A review of the use of computational intelligence in the design of military surveillance networks [M]. Heidelberg, Germany: Springer，2016: 663-693.

[8] Wu J, Ota K, Dong M X,et al. A hierarchical security framework for defending against sophisticated attacks on wireless sensor networks in smart cities[J]. IEEE Access, 2016(4):416-424.

[9] Zhu C, Zheng C L, Shu L, et al. A survey on coverage and connectivity issues in wireless sensor networks[J]. Journal of Network and Computer Applications, 2012, 35(2): 619-632.

[10] Mini S, Udgata S K, Sabat S L. Sensor deployment and scheduling for target coverage problem in wireless sensor networks[J]. IEEE Sensors Journal, 2014, 14(3): 636-644.

[11] Megerian S, Koushanfar F, Potkonjak M. Worst and best-case coverage in sensor networks[J]. IEEE Transactions on Mobile Computing, 2005, 4(1): 84-92.

[12] Meguerdichian S, Koushanfar F, Qu G, et al. Exposure in wireless ad-hoc sensor networks[C]∥Proceedings of the 7th Annual International Conference on Mobile Networking & Computing. Rome, Italy: ACM, 2001:139-150.

[13] Clouqueur T, Phipatanasuphorn V, Ramanathan P, et al. Sensor deployment strategy for target detection[C]∥Proceedings of the 1st ACM International Workshop on Wireless Sensor Networks & Applications. Atlanta, GA, US: ACM, 2002: 42-48.

[14] Gelfand I M, Fomin S V. Calculus of variations[M]. Heidelberg, Germany: Springer, 1966: 727-751.

[15] Djidjev H N. Approximation algorithms for computing minimum exposure paths in a sensor field[J]. ACM Transactions on Sensor Networks, 2010, 7(3): 145-153.

[16] Veltri G, Huang Q F, Qu G, et al. Minimal and maximal exposure path algorithms for wireless embedded sensor networks[C]∥International Conference on Embedded Networked Sensor Systems. Los Angeles, CA, US:IEEE, 2003.

[17] Djidjev H N. Efficient computation of minimum exposure paths in a sensor network field[C]∥Proceedings of the International Conference on Distributed Computing in Sensor Systems. Santa Fe, NM, US: Springer, 2007: 295-308.

[18] Zhang W Z, Li M L, Shu W，et al . Smart path-finding with local information in a sensory field[C]∥2nd International Conference on Mobile Ad-hoc and Sensor Networks . Hong Kong, China: IEEE，2006.

[19] Zhou J. A nodal integration and post-processing technique based on Voronoi diagram for Galerkin meshless methods[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(35): 3831-3843.

[20] Megerian S, Koushanfar F, Qu G, et al. Exposure in wireless sensor networks: theory and practical solutions[J]. Wireless Networks, 2002, 8(5): 443-454.

[21] Liu L, Zhang X, Ma H D. Minimal exposure path algorithms for directional sensor networks[J]. Wireless Communications and Mobile Computing, 2014, 14(10): 979-994.

[22] Liu X S, Kang G X, Zhang N B. Percolation theory-based exposure-path prevention for 3D-wireless sensor networks coverage[J]. KSII Transactions on Internet & Information Systems, 2015, 9(1): 126-148.

[23] Feng H, Luo L, Wang Y, et al. A novel minimal exposure path problem in wireless sensor networks and its solution algorithm[J]. International Journal of Distributed Sensor Networks, 2016, 12(8): 1550147716664245.

[24] Liu L, Song Y N, Zhang H Y. Physarum optimization: a biology-inspired algorithm for the steiner tree problem in networks[J]. IEEE Transactions on Computers, 2015, 64(3): 818-831.

[25] Yang T H, Jiang D L, Fang H Y. Target guiding self-avoiding random walk with intersection algorithm for minimum exposure path problem in wireless sensor networks[J]. EURASIP Journal on Wireless Communications and Networking, 2018(1): 33.

[26] 罗卿, 林亚平, 尹波. 传感器区域中基于网格的穿越轨迹算法研究 [J]. 通信学报, 2011, 32(6): 67-77.

LUO Qing, LIN Ya-ping, YIN Bo. Traversal trajectory based on grid in wireless sensor networks field[J]. Journal on Communications, 2011, 32(6): 67-77. (in Chinese)

[27] Liu L, Han G, Wang H. Obstacle-avoidance minimal exposure path for heterogeneous wireless sensor networks[J]. Ad Hoc Networks, 2017, 55:50-61.

[28] Liu L, Zhang X, Ma H D. Minimal exposure path algorithms for directional sensor networks[C]∥IEEE Conference on Global Telecommunications. Honolulu, Hawaii, US: IEEE, 2009:6155-6160.