中间轴的相位角优化设计

吴林涛

(天合汽车科技(上海)有限公司亚太技术中心，上海 201800)

0 引言

中间轴是汽车转向系统中的主要运动部件之一，具有传递扭矩、溃缩和良好的NVH表现。汽车转向系统有多种形式，目前较为常见的是管柱式电动助力转向系统(Column Drive Electric Power Steering, CD-EPS)，中间轴在此系统中连接了转向管柱和转向器(如图1所示)。

中间轴由上下两个万向节叉和公母轴装配而成，结构简单，可传递功率大。但是万向节传动具有不等速的运动特性，会产生力矩和传动比波动的问题，严重影响了驾驶的舒适性和安全性。如何避免力矩波动一直是汽车转向系统设计过程中一项重要的指标，特别是现阶段用户对汽车的要求越来越高。文中将通过理论分析结合实际情况，介绍中间轴相位角对力矩和传动比波动的影响，以及在实际设计中如何选择最佳相位角。

1 万向节传动的运动分析

对单万向节传动进行分析(如图2所示)，可得普通十字轴万向节的主动轴和从动轴转角的关系[1]为：

tanφ1=tanφ2·cosα

(1)

式中：φ1为主动轴叉转角；φ2从动叉转角；α为主动轴和从动轴的夹角。

图2 运动分析简图

由式(1)可得：

(2)

式中：ω1是输入轴的转速；ω2为输出轴的转速。

很明显，式(2)是周期为π的周期函数，即主动轴转一周，传动比ω2/ω1经历两个周期循环。由此可知，当主动轴以恒定速度转动时，从动轴时快时慢，这就是普通十字轴万向节传动的不等速特性。

目前汽车乘用车设计中，几乎所有的中间轴都是双十字轴万向节传动。所以，以下内容将重点介绍和分析双十字轴万向节传动的运动特性。

众所周知，双十字轴万向节等速传动的条件是[2]：(1)转向管柱、中间轴和转向机齿轮轴中心线在一个平面内； (2)转向轴和中间轴的夹角与中间轴和转向机齿轮轴的夹角相等。

因为转向系统只能在有限的空间里设计布置，与其他零部件相互制约，所以前面所述的两个条件很难满足，转向系统输出端最终仍然有角速度波动(即传动比波动)和力矩波动。根据高晋等人[3]的研究，导致波动的主要原因是相邻两轴之间夹角的差异。除此以外，还可以通过对中间轴的相位角进行优化，以达到抑制波动的目的。

中间轴的相位角为下节叉相对上节叉转过的角度(锐角)，观察方向从点B(中间轴上节叉十字轴中心点)看向点C(中间轴下节叉十字轴中心点)，顺时针为负，逆时针为正(如图3所示)。

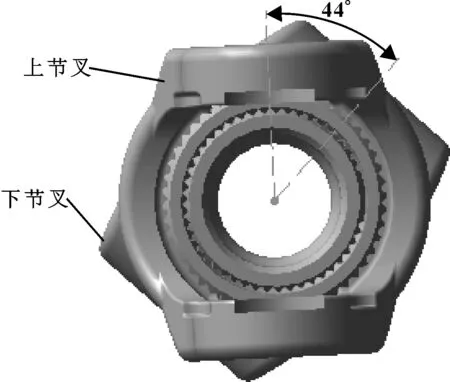
图3 相位角示意图

转向系统简图如图4所示。根据DUDITZA[4]的研究可知，双十字轴万向节传动的输出轴的转角公式如下：

式中：φ1为输入轴的转角；φ2为输出轴的转角；α1为输入轴与中间轴的夹角；α2为中间轴与输出轴的夹角；β为传动面的夹角(即转向管柱中心线AB和中间轴中心线BC形成的平面ABC与输出轴中心线CD和中间轴中心线BC形成的平面BCD之间的夹角)；γ为中间轴的相位角。

已知输出轴和输入轴的角速度比为：

式中：ω1和ω2分别是输入轴和输出轴的转速。

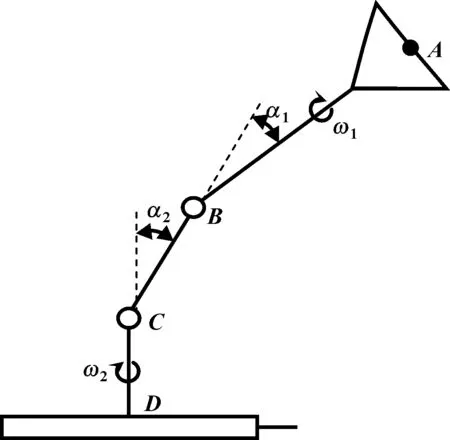
图4 转向系统简图

进一步分析可得：

c1=cosα1cosα2[tan2(γ-β)+1]

c2=tan2(γ-β)+cos2α2

c3=2tan(γ-β)cosα1[cos2(α2)-1]

c4=cos2α1[1+tan2(γ-β)cos2α2]

极值情况如下所示：

判定电动助力转向系统的角速度波动可用不均匀度百分比(Peak to Peak, P2P)。把φ1,1和φ1,2代入公式ω3/ω1可计算得到中间轴传动的不均匀度αP2P如下所示：

由此可以判断，影响角速度比波动的因素有传动角α1、α2和传动面夹角β，还有相位角γ。转向系统在车体内的布置空间非常有限，很难随意改变，而通过改变相位角来控制力矩波动成为主要手段。

根据李宁等人[5]的研究，当α1=α2且β=γ时，能实现等速传动；当α1≠α2，在β=γ时，输入轴和输出轴之间的转速差最小。所以，中间轴的相位角与传动面夹角相等时，为最佳相位角。

2 程序编制与验证

由于前面所述的理论分析相位角和传动比太复杂，为了便于在开发阶段设计中间轴，基于EXCEL VBA开发了一个相位角和角速度比的分析程序，此程序已通过实际验证，并在实际开发阶段运用了很多年，保证准确可靠，也得到了各大汽车主机厂的广泛认可。在该程序中，只需分别输入4个硬点坐标，即可得到理论计算的最佳相位角和输入输出轴的角速度比曲线图，各硬点相对位置也可直观地显示。

下面以国产某型号车型的电动助力转向系统为例。输入点A、B、C、D的坐标(如表1所示)，计算得到的数据如表2所示，其余的结果如图5—7所示。

从程序的计算结果可知：在相位角γ为43.73°时，角速度比波动最小。在设计图纸时，考虑到实际情况和工艺的实现，将该中间轴的相位角尺寸定义为44°±2°。

表1 各硬点坐标 mm

表2 程序计算结果

图5 传动比波动图

图6 硬点位置在XOZ平面的投影

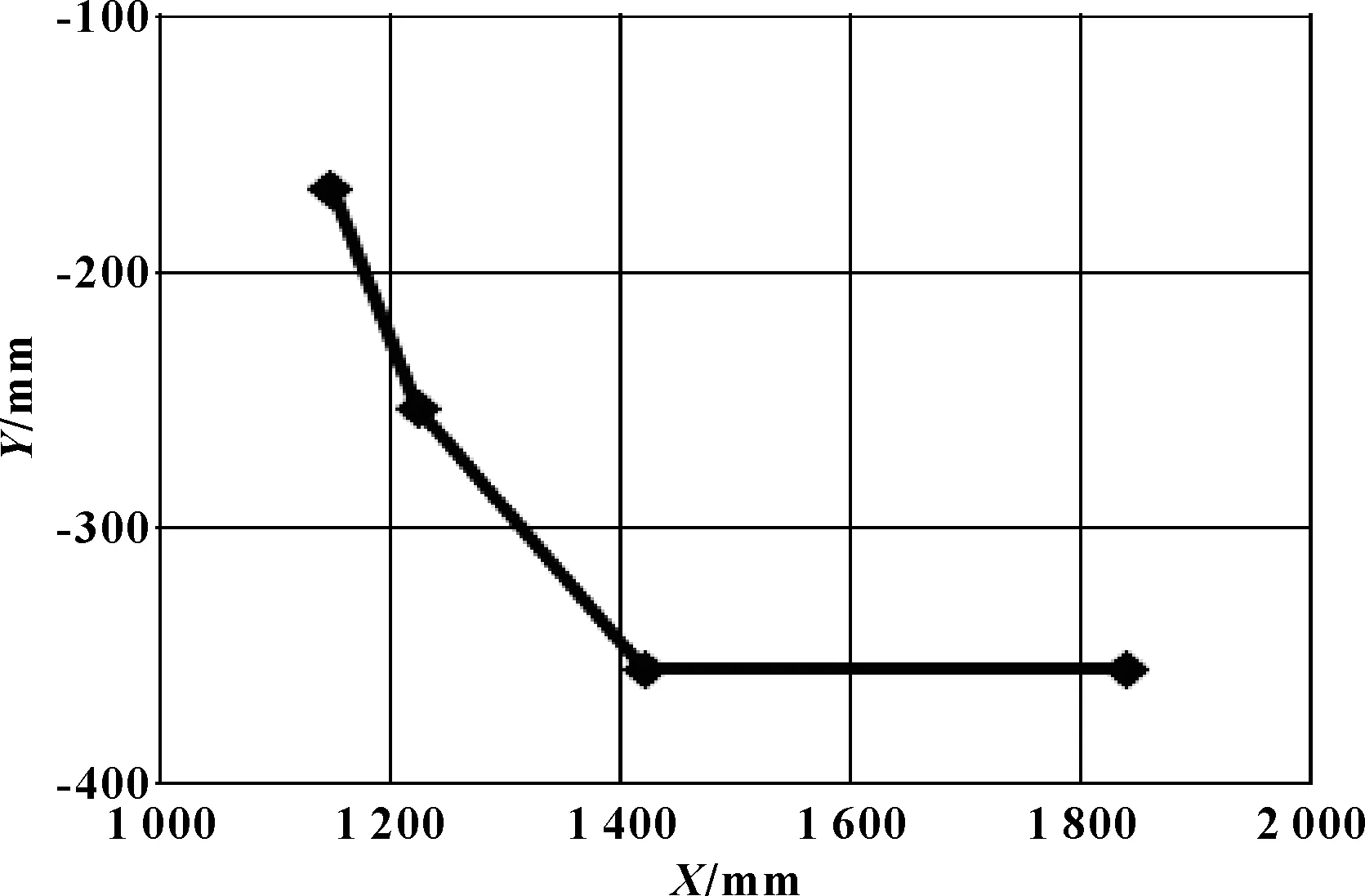
图7 硬点位置在XOY平面的投影

3 台架试验验证

对此型号的中间轴进行角速度波动试验，将中间轴模拟整车安装位置固定在试验台架上(如图8所示)，选取3件新品，试验结果如图9—11所示。

图8 试验安装示意图

图9 样件一试验结果

图10 样件二试验结果

图11 样件三试验结果

3次试验的数据分别是13.85%、12.72%和10.43%。可以看出：这3件中间轴都满足该项目对波动值小于15%的技术要求，所以以上3件新品在此项试验中都满足要求。

4 结束语

通过对十字轴万向节传动的运动分析，建立了中间轴角速度比和传动角方程，并通过理论分析结合实际情况，得出了抑制电动助力转向系统中间轴角速度波动的主要手段是优化中间轴的相位角，并且知道最佳相位角就是当相位角与传动夹角相等的时候。

在此基础上，还通过实例引出了某公司开发的相位角和角速度比分析程序，对汽车电动助力转向系统的设计及其他万向节传动的研究具有重大的实际意义。

参考文献:

[1]刘涛.汽车设计[M].北京：北京大学出版社，2008.

[2]胡国强,岳红旭.汽车转向系统十字轴万向节传动优化设计[J].汽车工程师,2011(7):30-33.

HU G Q,YUE H X.Optimization Design of Cardan Universal Joint Driving of Automotive Steering System[J].Auto Engineer,2011(7):30-33.

[3]高晋,牛子孺,杨秀建.双十字轴万向节转向系统不等速因素研究[J].机械设计与制造,2015(12):194-197.

GAO J,NIU Z R,YANG X J.Research of Steering System with Double Cross Universal Joints[J].Machinery Design & Manufacture,2015(12):194-197.

[4]DUDITZA F.Kardangelenkgetriebe und ihre Anwendungen[J].VDI-Verlag GmbH,1973,9(2).

[5]李宁,李友荣,周思柱,等.双十字轴万向节转向传动轴的相位角影响分析[J].机械传动,2015(9):15-19.

LI N,LI Y R,ZHOU S Z,et al.Influence Analysis of Phase Angle of Double Cross Universal Joint Steering Transmission Shaft[J].Journal of Mechanical Transmission,2015(9):15-19.