基于游程检测法重构集合经验模态的养殖水质溶解氧预测

宦 娟，曹伟建，秦益霖,2※，吴 帆

（1. 常州大学信息科学与工程学院，常州 213164；2. 常州旅游商贸高等职业技术学校，常州 213032）

0 引 言

水中溶解氧含量是池塘水质管理中最重要的问题之一[1]。溶解氧浓度对饲料消耗、代谢率和能量消耗有很大的影响[2]。例如，根据可靠的统计分析，在螃蟹养殖池塘里，由于溶解氧的过多或过少造成螃蟹死亡的数量占总死亡数的 50%左右。所以溶解氧的精细化管理对池塘养殖动物的健康非常重要。如何准确预测未来水中溶解氧变化趋势，建立准确、实用的预测模型对于水产养殖业具有重要的现实意义。

近年来，许多专家学者在溶解氧含量预测方面做出了许多工作，也取得了很大的成就。其预测方法主要有专家评估系统、数理统计法、时间序列、灰色理论法、神经网络法和支持向量回归机等。比如刘双印等[3-4]提出了用蚁群优化最小二乘支持向量机的预测模型，在此基础上又提出了一种基于WA-CPSO-LSSVR的混合预测模型预测养殖蟹池溶解氧，取得不错的预测效果。Ahmed提出利用人工神经网络进行预测的方法[5]，并应用自适应神经模糊推理系统来估计塞尔玛河溶解氧值[6]。Yan等[7]建立基于 BP神经网络的水质监测系统的溶解氧预测模型。这些方法利用现代智能算法自身的优势，在取得良好预测效果的同时，难免存在一些不足，比如欠学习和过学习、参数难以确定、易陷入局部最优等问题，无法满足对溶解氧预测的更高要求。而且这些方法直接在原始时序数据上建模，难以充分挖掘和利用各时频特征信息，尤其是溶解氧序列具有非线性和非平稳性的特点，这势必会影响上述方法的预测性能，所以对溶解氧序列进行降噪处理十分必要。而经验模态分解（empirical mode decomposition，EMD）是一种常用的处理时序数据非平稳性的方法。但基于经验模态分解方法的重要缺陷就是模态混叠。而集合经验模态分解（ensemble empirical mode decomposition，EEMD）通过加入服从正态均匀分布的白噪声来处理信号，能够有效的克服 EMD的缺陷[8-9]。它在预测领域也有广泛运用，张瑜等[10]基于EEMD与ELM神经网络建模，提出了一种线椒株高生长量的预测方法。徐龙琴等[11]提出集合经验模态分解和改进人工蜂群算法相结合的养殖池塘 pH值的组合预测模型。王贺等[12]将EEMD和LSSVM的组合预测模型引入到风速预测。

在借鉴前人研究的成果上，将EEMD用于溶解氧的预测，但是如果对EEMD分解后的多个分量一一建模预测，不仅会加大工作量，降低预测速度，而且对多个分量预测的结果进行叠加，无疑会增大误差[13]。本文提出了游程检测法重构EEMD的组合预测模型。该模型先将溶解氧序列用EEMD进行分解，分解出一系列不同频段的分量，再采用游程检测法将其重构为高频、中频、低频3种分量，再根据3种分量的变化特征，选择适宜的预测方法进行预测，最后对3种分量预测结果用BP神经网络进行重构，就获得最终预测结果。将该模型运用到江苏省溧阳市埭头黄家荡特种水产养殖场的溶解氧预测中，研究表明本方法具有较高的精度。

1 数据与方法

1.1 数据采集

以江苏省溧阳市埭头黄家荡特种水产养殖场为试验场地，养殖场占地面积1.53 km²，位于长荡湖南岸，距埭头镇5 km，水陆交通快速便捷，区域内环境优美，管理规范，配备有先进的现代化水产养殖设备，设施齐全。本试验选取场内一个 500 m²的标准池塘为试验区域，试验数据通过无线监控系统采集，其结构如图 1所示。该系统在水质监测节点上配备有 pH传感器、溶解氧传感器、水温传感器等，监测中心将采集到的各个水质参数，通过 GPRS送到服务器，用户就可以用手机、电脑实时监控。水质调控节点上配备有增氧泵等设备，从而能实现对水质的调控。本文溶解氧的数据源自该系统的数据库，该系统每隔1 h采集1次数据，选择2016年5月10日至6月24日共46 d的1 104个数据作为试验数据。选取前1 056个数据为训练集，后48个为测试集。

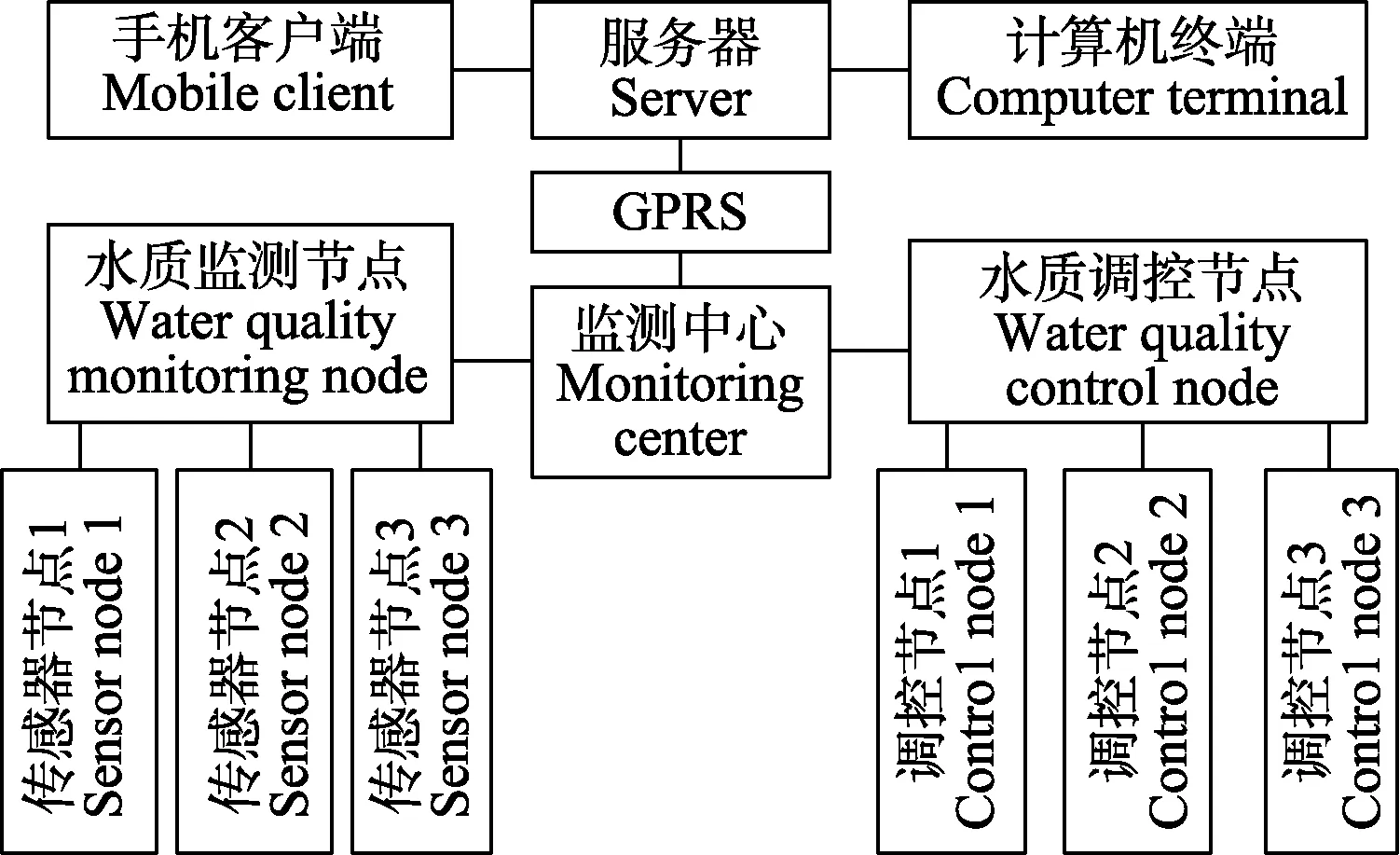
图1 水质远程监测系统结构图Fig.1 Wireless monitoring system of water quality

1.2 EEMD算法

EEMD是一种自适应信号分解方法，适用于分析非线性和不稳定过程，克服了模态混叠的问题[14-15]。EEMD将高斯白噪声引入到原始时间序列中，以不同尺度均匀分布于整个时间序列来避免模态混合，由于白噪声的随机性，可以通过充分的反复试验，可以降低相应的本征模函数(intrinsic mode function，IMF)的附加噪声。其分解步骤如下[16]：

1）在原始时间序列 y(t)中，添加一个服从(0，(αε)2)正态分布的白噪声u(t)，就得到了一个新的信号x(t)，其中 k是白噪声标准差与原始序列标准差的比例，一般在0.1和0.8之间，α为噪音强度参数，ε为信号的标准差；

2）按照EMD的分解方法[17]进行分解，分解成一组IMF分量Ci(t)和一个余量R(t)；

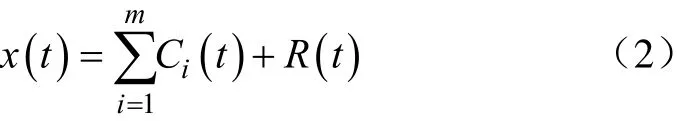
其中m是IMF的个数。

3）重复步骤（1）和步骤（2），并改变每次加入的白色噪声的振幅，得到A组不同的IMF分量和剩余分量；

4）将A组不同的IMF分量和剩余分量的总体平均值作为最终结果。

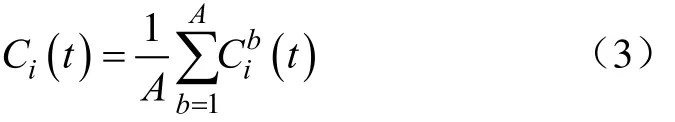
1.3 游程检测法

所谓游程是样本序列中连续出现的变量值的次数，游程检测是一种根据设定的样本标志游程的多少来进行判断的检验方法[18-19]，其目的是用于判断观察值的顺序是否随机。设某分量所对应的时间序列为{T(t)}(t=1, 2,…,N)，设其平均值为Tavg。

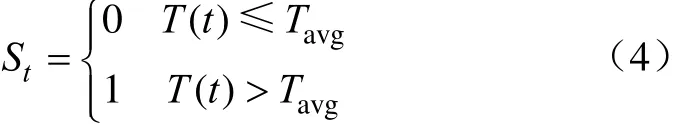
观察值比平均值Tavg小的就是负流程，记作“0”，观察值比平均值Tavg大的就是正流程，记作“1”，这样我们就得到一个 0-1序列。游程就是连续 1的个数和连续 0的个数，游程长度就是一个游程中的数据个数。通过 0和1出现的集中程度可以判断EEMD分量的波动程度。如果游程总数相比于设定的阈值大，且游程长度比较短，则说明此序列波动比较频繁；反之，游程总数少，游程长度长，意味着波动变化不频繁。综合考虑每个分量的游程数和游程长度，将EEMD分解后的序列重构为3个分量。

2 预测模型构建

在建模的过程中，首先将溶解氧时间序列通过EEMD分解成多个不同尺度的分量，再用游程检测法将所有分量重构成高频、中频和低频 3种分量，根据每个分量的特征，选择适宜的预测方法进行预测，最后用BP神经网络对 3种分量的预测结果进行重构得到最终的预测结果。其溶解氧的预测流程图，如图 2所示，具体步骤如下：

1）原始序列的EEMD分解。对于原始的溶解氧时间序列根据公式（1）~（3）进行 EEMD 分解，分解成 x个具有不同特征的本征模态分量IMF1~IMFx和一个剩余分量Res。

2）游程检测法重构。EEMD分解后，生成的 IMF分量较多，对每个分量都建立相应的预测模型，会增加难度和预测的工作量，这就需要对溶解氧序列分量进行重构。其重组步骤如下：

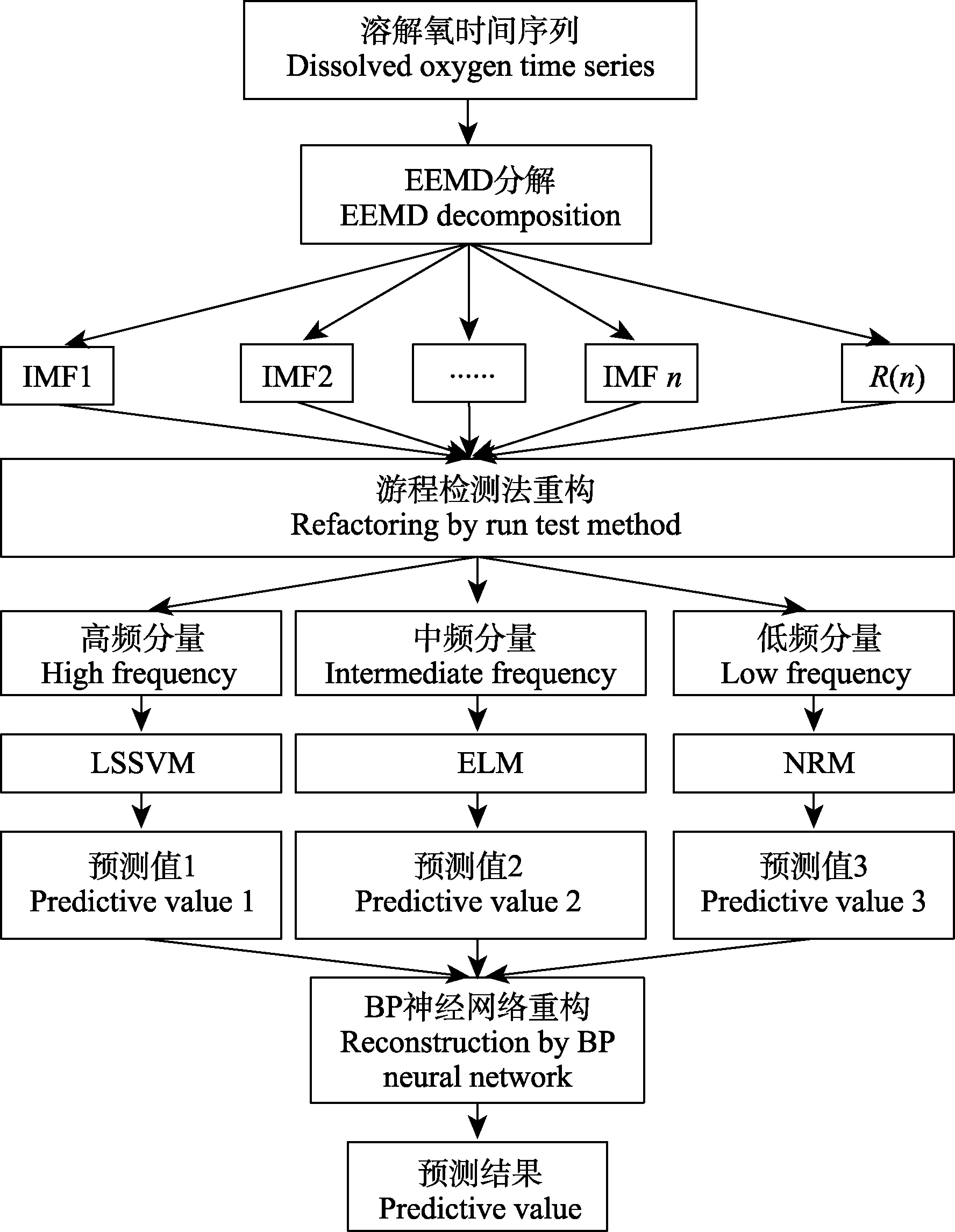
图2 溶解氧预测流程图Fig.2 Flowchart of dissolved oxygen prediction

Step 1 计算每个IMF和余量Res的游程数和每个分量的最大游程长度；

Step 2 根据每个分量的游程数和最大游程长度，选择游程数变化率最大的游程数作为阈值；

Step 3将每个分量的游程数分别与阈值比较，从而划分高频，中频和低频分量；

Step 4根据判断结果，分别叠加各个分量，最终得到所需的溶解氧重构序列。

3）选择合适的预测算法。针对高频、中频和低频 3种分量的特征，选择 LSSVM、ELM 等不同的预测算法进行建模训练和预测，让各算法间能够优势互补。

4）预测结果重构。不是将各分量的结果进行简单的叠加，而是用BP网络来进行非线性的叠加。

5）误差分析。选用均方根误差(RMSE)、平均相对误差均值(MAPE)和平均绝对误差(MAE)作为评价指标。

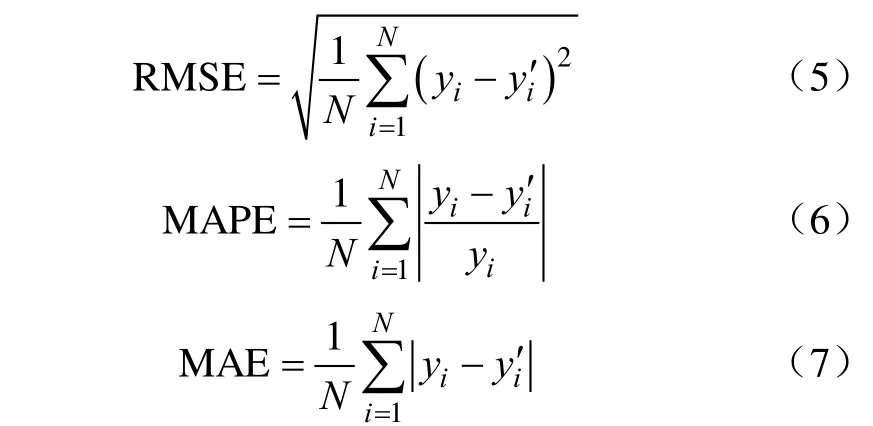
式中yi为真实值，yi’为预测值，N为样本总数。

3 试验与结果分析

3.1 基于EEMD的溶解氧时间序列分解

根据第1.2节所述的EEMD分解步骤，对非线性和非平稳性的溶解氧序列进行分解。通过文献[20]可知，本文设置N为100，α的值是0.2，ε值是0.25。溶解氧时间序列被分解成9个IMF分量和一个余项。其分解结果如图3所示。

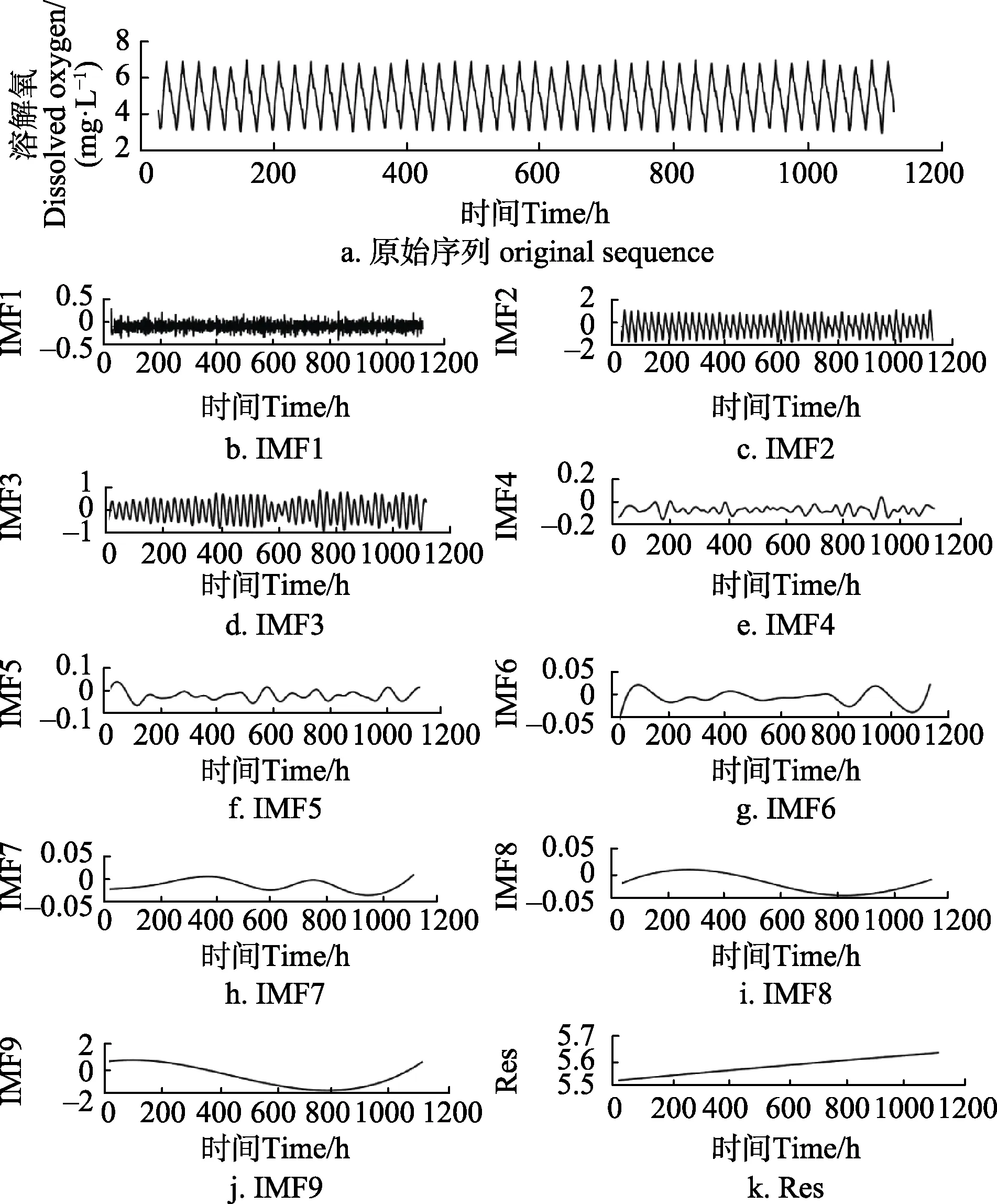
图3 EEMD分解结果图Fig.3 EEMD decomposition results

从图 3中可以看出，溶解氧原始时间序列具有十分明显的非线性和非平稳性的特征。9个IMF分量反应了原始溶解氧信号不同的波动信息，余项 Res反映了溶解氧长期的变化趋势。

3.2 游程检测法重构

考虑到EEMD分解后分量过多，且根据每个分量的特征一一建立相应的预测模型有困难。因此在保证序列平稳性的前提下，采用游程检测法将多个IMF分量和一个余量重构成高频分量、中频分量和低频分量。计算各分量的游程总数和最大游程长度，结果如表1所示。

表1 分量的游程数与最大游程长度Table 1 Runs number and maximum runs length of IMF components

综合考虑游程总数和最大游程长度，将IMF1作为高频分量，将IMF2~IMF8叠加作为中频分量，将剩余分量Res与IMF9叠加作为低频分量。

3.3 不同尺度序列的单项预测

根据高频、中频和低频 3种分量的特征，选择合适的预测算法来进行多步预测。重构结果如图 4所示。从图 4中可以看出，其中高频分量具有波动较大、变化复杂等特点，所以本文选择鲁棒性强、计算复杂度低、收敛速度快且拟合精度高的最小二乘支持向量机（least square support vector machine，LSSVM）算法[21-22]进行预测。并用粒子群算法优化最小二乘支持向量机的核参数σ和惩罚参数 C，使其能有更高的预测精度[12]。优化后得到σ=25.12，C=1.55；对于具有周期性的中频分量，本文采用极限学习机（extreme learning machine，ELM）对其进行预测。因为ELM经常用于非线性预测[23-24]，具有设置参数方便、泛化能力强等特点。本文选用Sigmoid函数作为ELM算法的激励函数，设置网络隐含层节点数为8；低频分量变化比较平缓，所以采用非线性回归（nonlinear regression，NRM）的方法进行预测。

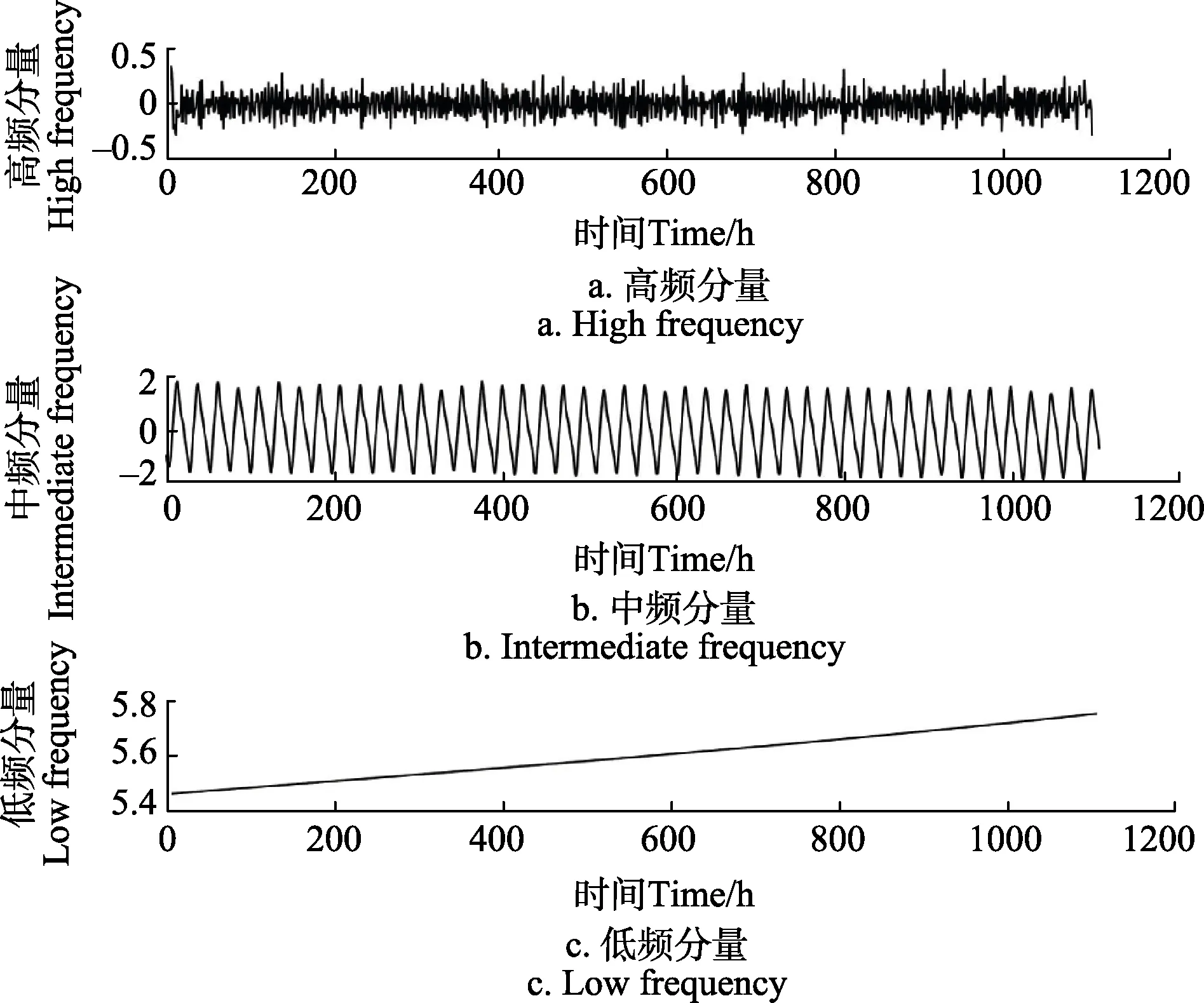
图4 各个IMF分量的重构结果图Fig.4 Reconstruction results of IMF components

3.4 BP神经网络结果重构

BP神经网络（BP artificial neural network，BPANN）是目前最广泛使用的神经网络模型之一[25-26]。BPANN的实现过程是信号来自输入层，在隐藏层中处理，输出层里输出，是根据预测误差来调整权值和阈值，从而使BP神经网络的输出不断逼近期望值。

本文在对最后的预测结果的处理中，不再采用直接叠加，而是用BP神经网络对预测结果进行非线性叠加，使其能达到更好的预期效果。将高频、中频和低频 3个分量的预测结果作为输入因子，因此输入层节点为3。输出因子为溶解氧的预测结果，节点数为1，通过对不同隐含层神经元数进行训练对比后，确定隐含层节点数确定为5，所以BP神经网络结构为3-5-1。设定BP神经网络的相关参数，如较小的学习因子能保证系统的稳定性，所以学习速率设定为0.01；设置学习因子φ=0.7；通过对网络的训练，再考虑综合因素，选取网络的期望误差为0.000 2；因为Sigmoid函数容错性较好，所以选择Sigmoid函数作为激励函数。

3.5 模型预测结果及对比分析

3.5.1 重构误差分析

由于本文所提出方法的预测值是由高频、中频和低频这3个分量的预测值是通过BPANN进行非线性叠加得到的，那么最终预测结果的误差也是由这 3个分量的预测误差和BP神经网络重构时的误差构成的。为了更好地分析这3个分量的预测误差和BPANN重构的误差对最终预测结果影响，本文将 3个分量预测值与真实值进行比较，将用BPANN非线性叠加得到的预测值，用自适应叠加得到的预测值与真实值进行比较。3个分量的预测值与真实值的对比如图5所示。

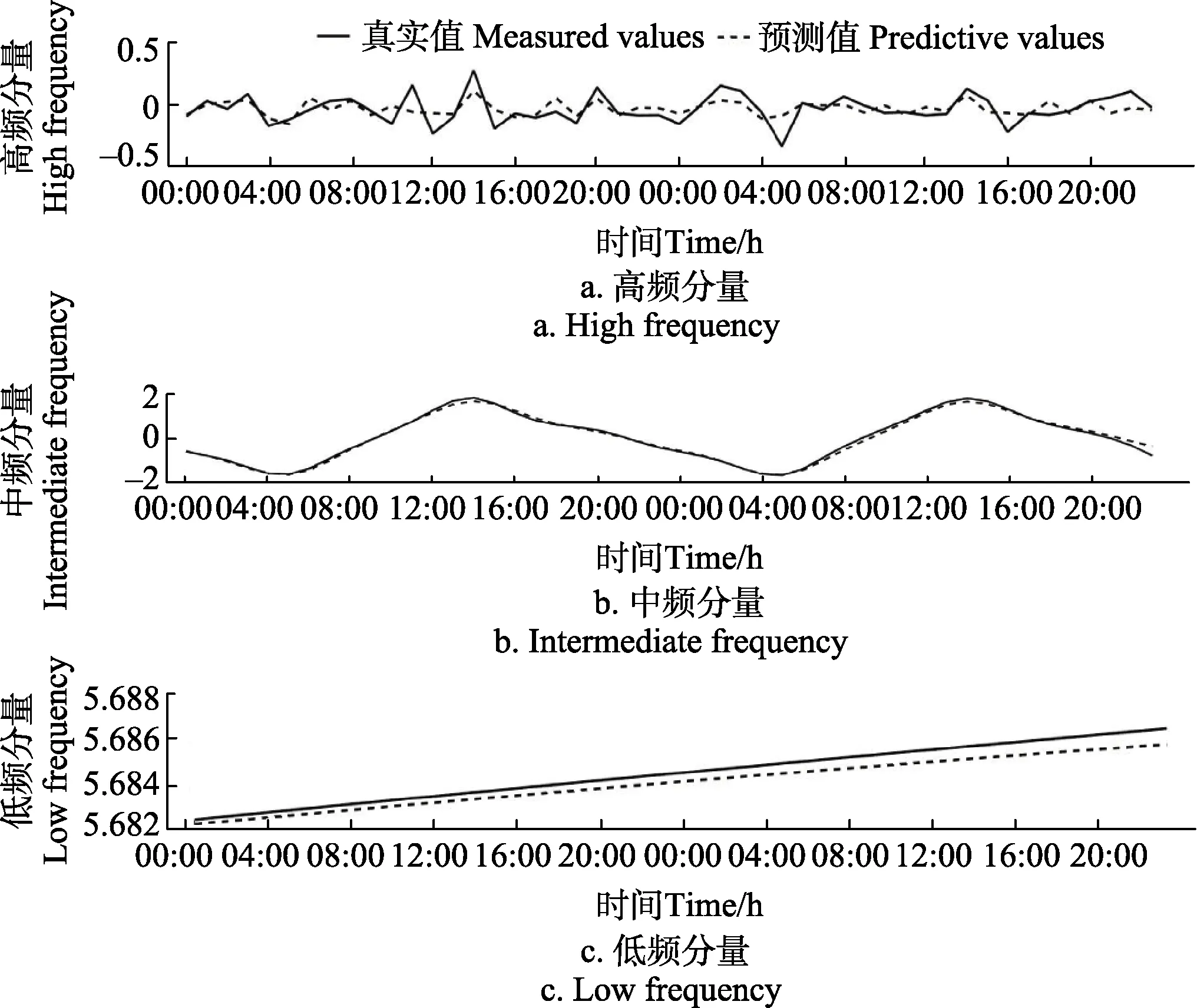
图5 三分量的预测值和真实值对比Fig.5 Three components comparison between forecasting values and measured values

从图 5中可以看出，在拟合效果上，从低频分量到高频分量呈现下降的趋势，主要是高频分量拟合效果不佳。计算低频、中频和高频这 3个分量预测结果的均方根误差分别是0.000 7、0.073 5和0.164 2，由此可以看出，误差主要集中在高频分量，亦可以说本文所提出的模型误差主要来自于重构的高频分量。

本文通过决定系数 R2和均方根误差 RMSE来验证BPANN非线性叠加效果。自适应叠加的预测值与真实值的对比如图 6a所示，BPANN非线性叠加的预测值与真实值的对比如图6b所示。

由图6可知，本文用BP神经网络非线性叠加得到的预测结果的决定系数R2为0.995 5，而用自适应叠加得到的预测结果的R2为0.990 2，再计算BP神经网络非线性叠加和自适应叠加后的均方根误差分别为 0.099 2和0.111 9，表明，3个分量的预测结果经过BP神经网络非线性叠加后得到的预测值的精度要比直接自适应叠加的高，进而说明了本文所提方法的有效性。

3.5.2 模型预测结果分析

为了评估本文所提出模型的性能，本文选用粒子群优化的最小二乘支持向量机（PSO-LSSVM）模型和传统的极限学习机（ELM）模型与本文所提出的“分解-重构-预测-重构”模型进行比较。PSO-LSSVM和标准ELM都是经典常用的预测模型，两者都具有一定的代表性。这2种模型在预测时采用直接预测的方法，并不进行分解。3种模型采用相同的试验数据预测2016年6月23日、2016年6月24日2 d共48个溶解氧值。3种模型的预测曲线对比如图7所示。

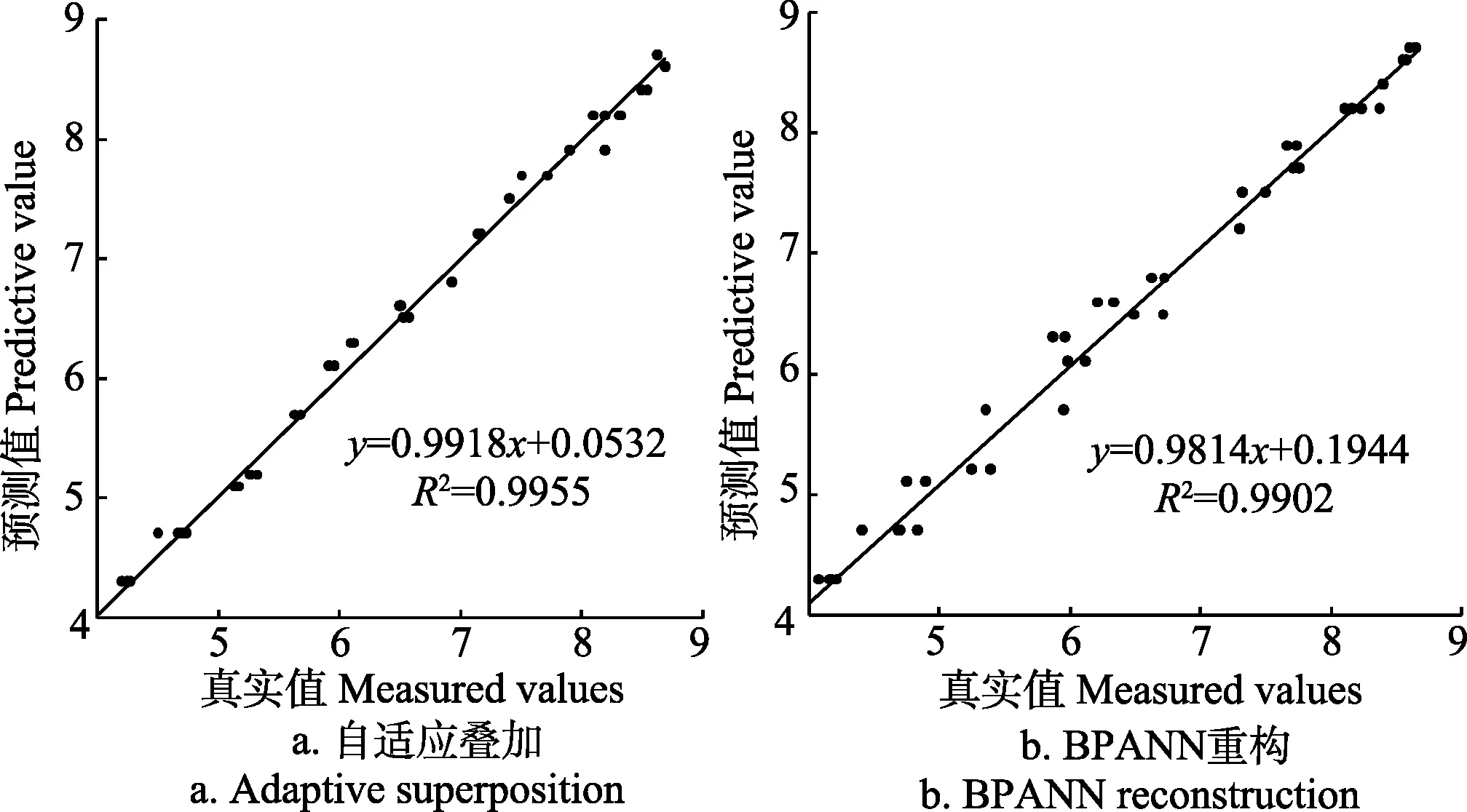
图6 自适应叠加的和BPANN重构的预测结果图Fig.6 Forecast results by adaptive superposition and BPANN reconstruction

从图 7中可以看到，本文组合模型的预测结果曲线比PSO-LSSVM和ELM预测曲线更加接近真实值曲线。由此说明，本文所提出的用游程检测法重构EEMD的组合预测方法有好的预测精度，比其他 2种模型更能拟合好溶解氧时间序列。

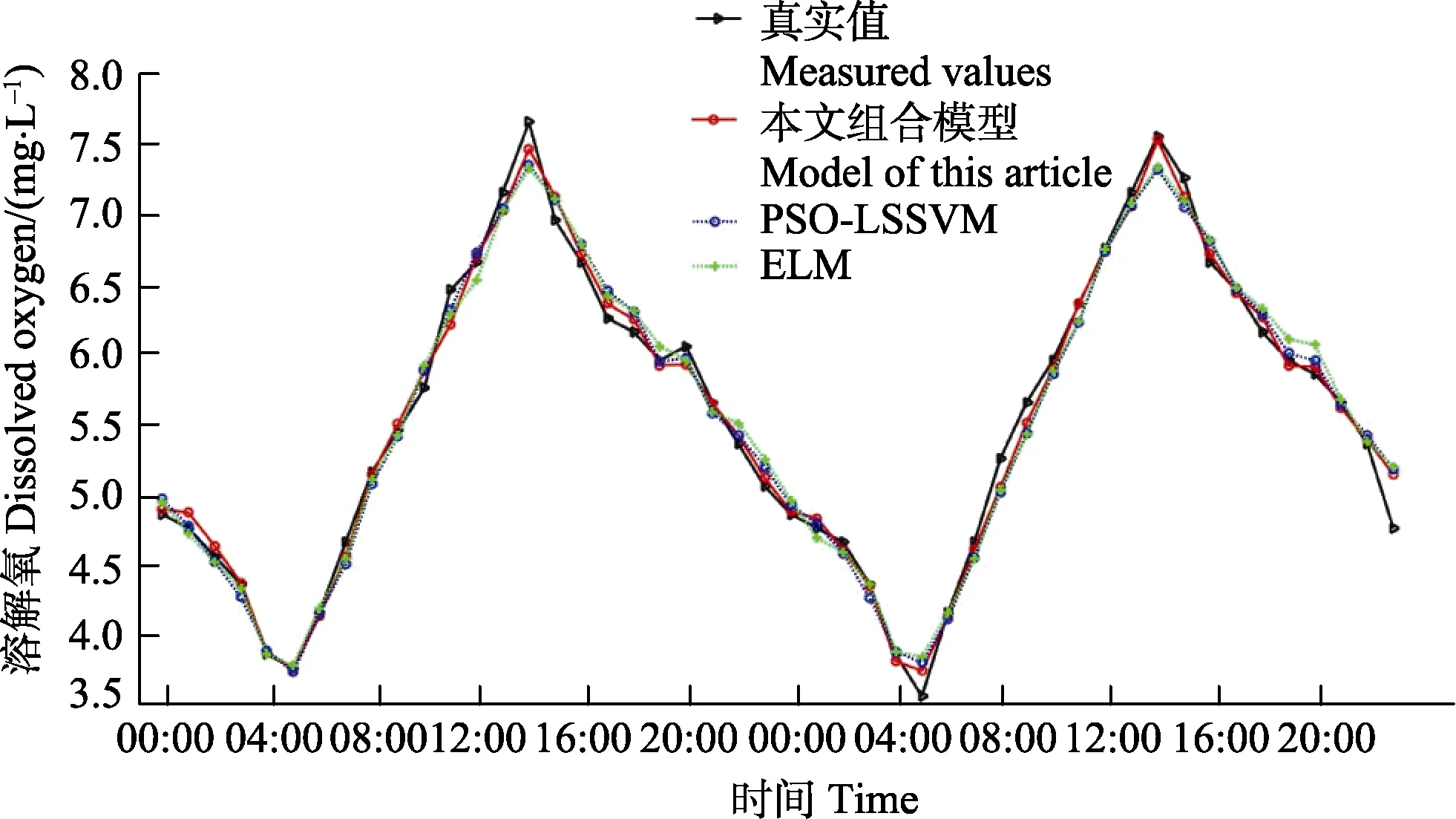
图7 3种模型的预测结果曲线（2016-06-23―06-24）Fig.7 Predictive results curve of three predictive models

为了进一步比较 3种预测模型，本文计算出它们的均方根误差(RMSE)、平均相对误差均值(MAPE)和平均绝对误差(MAE)，其预测精度统计结果如表2所示。

从表 2中可以看出，本文所提出的模型具有较低的误差。在预测未来12 h溶解氧值时，3种模型预测精度都较高，本文所提出模型的效果略比 PSO-LSSVM 和ELM好，但其优势不是太明显；进一步分析预测未来24 h溶解氧值时的均方根误差、平均相对误差均值和平均绝对误差的变化，可以发现本文所提模型的 3种指标比PSO-LSSVM的分别下降了0.020 5，0.020 2和0.002 2，比ELM的分别下降了0.031 2，0.030 9和0.000 7，从中可以发现PSO-LSSVM比ELM有较好的预测效果，本文提出的模型比这 2种模型具有更好的预测效果；接着再比较预测未来36和48 h溶解氧的误差，其均方根误差比PSO-LSSVM分别下降了0.024 4和0.035 2，比ELM分别下降了0.034 5和0.058 9，其他2项指标也有较大幅度的下降，所以本文所提出的用游程检测法重构 EEMD，并选择合适预测算法的模型比PSO-LSSVM和标准ELM预测模型的预测精度高。表 2中，本文方法在预测未来12、24，36和48 h溶解氧的均方根误差分别为0.088 6，0.093 1，0.095 7和0.099 2，可以看出随着预测时长的增加，误差也会越来越大，PSO-LSSVM 模型和标准 ELM模型也存在同样的问题。但是，本文提出的模型在预测24 h时的均方根误差比预测12 h 增加0.004 5，预测36 h时比预测12 h增加0.007 1，预测48 h时比预测12 h增加0.010 6，而PSO-LSSVM在预测24，36和48 h时的均方根误差比预测12 h分别增加0.016 8，0.023 3和0.037 6，标准ELM在在预测24，36和48 h时的均方根误差比预测12 h分别增加0.031 5，0.037 4和0.065 3，在长时间的预测中，本文提出的模型误差递增速度比其他 2种模型慢，所以本文所提出的模型更具有稳定性，比其他2种模型更加适合长时间的预测。

表2 3种模型预测误差指标对比Table 2 Comparison of error index of forecasting

3.5.3 讨 论

本文使用 EEMD对溶解氧时间序列进行多尺度分解，不仅避免了EMD分解出现的模态混叠的问题，而且降低了原始序列各特征之间的相互干扰，降低了非平稳性，更加深入的挖掘出溶解氧序列的信息。

针对EEMD分解后，产生的分量过多，会加大预测工作量的问题，本文用游程检测法重构EEMD分解后的分量，这样能大大减少计算量，降低误差，还能使重构的分量更加直观有效的反映出溶解氧原始信号的特征。

对于重构后的分量，本文根据各个分量的特征选择相适宜的预测方法，从而使各算法间能够优势互补，达到更好的预测结果。

本文方法还存在一些不足，第一，针对高频分量预测误差较大的问题，其原因是高频分量波动性大，还有预测算法LSSVM的参数难以确定，虽然使用了粒子群算法进行优化，然而却不能避免其自身早熟收敛的问题，在今后的研究中，可对LSSVM算法和粒子群算法进行改进，从而能使精度得以提高；第 2个问题是预测误差随着时长的增加越来越大，这是因为溶解氧会受天气、季节、水温、氨氮量等其他因素的影响且实时性较强，可以综合考虑天气等因素的重要影响，通过适时更新训练数据来提高预测精度，使本方法能快速应对突变天气对溶解氧的影响。

4 结 论

本文利用集合经验模态分解、游程检测法和BP神经网络等方法，构造了一种“分解—重构—预测—重构”的养殖池塘溶解氧预测模型，首先对采集到的原始溶解氧信号进行EEMD分解，再用游程检测法将分解后的多个分量重构成高频、中频和低频 3种分量，随后根据每个分量的特征选择合适的预测算法，高频分量预测选用鲁棒性强的最小二乘支持向量机（least square support vector machine，LSSVM）算法，并用粒子群算法优化它的参数，中频分量选用速度快、泛化能力强的极限学习机(extreme learning machine，ELM)算法进行预测，低频分量选用非线性回归的方法进行预测，最后将 3个分量的预测结果用BP神经网络进行重构，得到最终的预测结果。试验结果表明，与粒子群优化的最小二乘支持向量机和ELM相比，本文提出的模型有较好的预测结果，更高的预测精度。本文采用BP神经网络非线性叠加取代简单的自适应叠加，取得了更好的拟合效果，该模型的预测值与实测值的相关决定系数为0.995 5、均方根误差为0.099 2。本文所提出的方法能够使养殖人员较快的得到未来溶解氧变化的信息，为他们的决策提供科学的支撑，从而降低养殖风险。

[参 考 文 献]

[1] 胡金有，王靖杰，张小栓，等. 水产养殖信息化关键技术研究现状与趋势[J]. 农业机械学报，2015，46(7)：251－263.Hu Jinyou, Wang Jingjie, Zhang Xiaoshuan, et al. Research status and development trends of information Technologies in aquacultures[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(7): 251－263. (in Chinese with English abstract)

[2] Buentello J A, Gatlin D M, Neill W H. Effects of water temperature and dissolved oxygen on daily feed consumption,feed utilization and growth of channel catfish (Ictalurus punctatus)[J]. Aquaculture, 2000, 182(4): 339－352.

[3] 刘双印，徐龙琴，李道亮，等. 基于蚁群优化最小二乘支持向量回归机的河蟹养殖溶解氧预测模型[J]. 农业工程学报，2012，28(23)：167－175.Liu Shuangyin, Xu Longqin, Li Daoliang. Dissolved oxygen prediction model of eriocheir sinensis culture based on least squares support vector regression optimized by ant colony algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012,28(23): 167－175. (in Chinese with English abstract)

[4] Liu S, Xu L, Jiang Y, et al. A hybrid WA–CPSO-LSSVR model for dissolved oxygen content prediction in crab culture[J]. Engineering Applications of Artificial Intelligence,2014, 29(3): 114－124.

[5] Ahmed A A M. Prediction of dissolved oxygen in Surma River by biochemical oxygen demand and chemical oxygen demand using the artificial neural networks (ANNs)[J].Journal of King Saud University-Engineering Sciences, 2017,29(2): 151－158.

[6] Ahmed A A M, Shah S M A. Application of adaptive neuro-fuzzy inference system (ANFIS) to estimate the biochemical oxygen demand (BOD) of Surma River[J].Journal of King Saud University-Engineering Sciences, 2015,29(3): 237－243.

[7] Yan J X, Yu L J, Mao W W, et al. Study on prediction model of dissolved oxygen about water quality monitoring system based on BP neural network[J]. Advanced Materials Research, 2014, 912/913/914: 1407－1411.

[8] Kong Y, Meng Y, Li W, et al. Satellite image time series decomposition based on EEMD[J]. Remote Sensing, 2015,7(11): 15583－15604.

[9] Wu Zhaohua, Ne Huang. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009, 1(1): 0900004.

[10] 张瑜，汪小旵，孙国祥，等. 基于集合经验模态分解与Elman神经网络的线椒株高预测[J]. 农业工程学报，2015，31(18)：169－174.Zhang Yu, Wang Xiaochan, Sun Guxiang, et al. Prediction of cayenne pepper plant height based on ensemble empirical mode decomposition and Elman neural network[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(18): 169－174. (in Chinese with English abstract)

[11] 徐龙琴，李乾川，刘双印，等. 基于集合经验模态分解和人工蜂群算法的工厂化养殖pH值预测[J]. 农业工程学报，2016，32(3)：202－209.Xu Longqin, Li Qianchuan, Liu Shuangyin, et al. Prediction of pH value in industrialized aquaculture based on ensemble empirical mode decomposition and improved artificial bee colony algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016,32(3): 202－209. (in Chinese with English abstract)

[12] 王贺，胡志坚，张翌晖，等. 基于聚类经验模态分解和最小二乘支持向量机的短期风速组合预测[J] . 电工技术学报，2014，29(4)：237－245.Wang He, Hu Zhijian, Zhang Yihui, et al. A hybrid model for short-term wind speed forecasting based on ensemble empirical mode decomposition and least squares support vector machines[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 237－245. (in Chinese with English abstract)

[13] Wang Shouxiang, Wang Yamin, Liu Yan, et al. Hourly solar radiation forecasting based on EMD and ELM neural network[J]. Electric Power Automation Equipment, 2014,34(8): 7－12.

[14] Wang T, Zhang M, Yu Q, et al. Comparing the application of EMD and EEMD on time-frequency analysis of seimic signal[J]. Journal of Applied Geophysics, 2012, 83(6): 29－34.

[15] Jiang H, Li C, Li H. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis[J].Mechanical Systems & Signal Processing, 2013, 36(2): 225－239.

[16] Ding G, Wang L, Shen P, et al. Sensor fault diagnosis based on ensemble empirical mode decomposition and optimized least squares support vector machine[J]. Journal of Computers, 2013, 8(11) . DOI: 10.4304/jcp.8.11.2916-2924

[17] Wang X, Wang Y. A hybrid model of EMD and PSO-SVR for short-term load forecasting in residential quarters[J].Mathematical Problems in Engineering, 2016(5): 1－10.

[18] 李乐，刘天琪，陈振寰，等. 基于 EEMD 和 ARCH 的风电功率超短期预测[J]. 电测与仪表，2015，52(18)：16－21.Li Le, Liu Tianqi, Chen Zhenhuan, et al. Ultra-short-term wind power forecasting based on EEMD and ARCH[J].Electrical Measurement & Instrumentation, 2015, 52(18): 16－21. (in Chinese with English abstract)

[19] 于群，朴在林，胡博. 基于EEMD和BP神经网络的短期光伏功率预测模型[J]. 电网与清洁能源，2016，32(7)：132－137.Yu Qun, Piao Zailin, Hu Bo. A Hybrid model for short-term photovoltaic power forecasting based on EEMD-BP combined method[J]. Power System & Clean Energy, 2016,32(7): 132－137. (in Chinese with English abstract)

[20] Huanga E, Shen Z, Long S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454:903－995.

[21] Sun W, He Y, Chang H. Forecasting fossil fuel energy consumption for power generation using QHSA-based LSSVM Model[J]. Energies, 2015, 8(2): 939－959.

[22] 江田汉，束炯. 基于LSSVM的混沌时间序列的多步预测[J]. 控制与决策，2006，21(1)：77－80.Jiang Tianhan, Shu Jiong. Multi-step prediction of chaotic time series using the least squares support vector machines[J].Control & Decision, 2006, 21(1): 77－80. (in Chinese with English abstract)

[23] Huang G B, Chen L, Siew C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes[J]. IEEE Trans Neural Netw, 2006,17(4): 879－892.

[24] Huang G B, Zhou H, Ding X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics, 2012, 42(2): 513.

[25] Chen Y, Xu J, Yu H, et al. Three-dimensional short-term prediction model of dissolved oxygen content based on PSO-BPANN algorithm coupled with Kriging interpolation[J]. Mathematical Problems in Engineering,2016(1): 1－10.

[26] 朱成云，刘星桥，李慧，等. 工厂化水产养殖溶解氧预测模型优化[J]. 农业机械学报，2016，47(1)：273－278.Zhu Chengyun, Liu Xingqiao, Li Hui, et al. Optimization of prediction model of dissolved oxygen in industrial aquaculture[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(1): 273－278. (in Chinese with English abstract)