交变温度对航天轴承摩擦力矩的影响机理

宁峰平，樊晓琴，陈 然，安静涛，赵永生※

（1. 中北大学机械工程学院，太原 030051；2. 中国空间技术研究院天津航天机电设备研究所，天津 300301；3. 燕山大学河北省并联机器人与机电系统实验室，秦皇岛 066004）

0 引 言

随着航天技术的飞速发展，航天机构的功能日趋丰富，可靠性要求也越来越高。航天轴承作为航天机构中必不可少的关键元件，其可靠性是世界航天技术的主要难点之一[1-2]。由于空间环境的严酷性、极端性和不确定性，交变温度为空间环境温度在-60～80 ℃之间交替变化。交变温度严重影响航天轴承摩擦力矩的大小和稳定性，影响航天轴承运行的可靠性，进而影响航天机构的寿命、精度、可靠性。

为了适应极端复杂的空间环境，航天轴承表面溅射多种多样的固体润滑膜[3-4]。针对空间环境对航天轴承可靠性的影响，Ning等[5-6]根据轴承与轴系的变形协调关系探究了交变温度对轴承预紧力的作用机理。古乐等[7]针对空间环境建立空间轴系及其各组成轴承单元工作时的接触载荷与间隙数学模型，分析了交变温度导致轴承间隙变化的规律。徐志栋等[8]利用试验手段探讨了轴向载荷、高温和保持架类型对航天轴承摩擦力矩特性的影响。在空间环境中，交变温度和高真空对航天轴承的摩擦和磨损影响显著[9-10]。

航天轴承摩擦力矩大小不当将导致航天机构失效，因此摩擦力矩的动态性能是制约航天机构寿命及可靠性的重要因素[11-12]。Palmgren[13]通过试验获得轴承摩擦力矩计算的经验公式。Snare[14-16]在拟静力学基础上进行了轴承弹性滞后摩擦力矩、滑动摩擦力矩和自旋摩擦力矩理论分析并进行了试验研究。邓四二等[17-18]在动力学和热力学基础上，建立角接触球轴承摩擦力矩理论数学模型，并对影响因素影响摩擦力矩的机理进行了理论分析和试验验证。Gonçalves等[19]在恒定负载、不同工作温度下，研究了温度和转速对摩擦力矩的影响。在预紧状态下，Ghanbari等[20]通过试验研究给出运转速度、工作载荷与摩擦力矩的关系式。目前，针对摩擦力矩的研究，国内外众多学者分别从结构参数[21-22]、表面参数[23]、润滑条件[24]、轴承转速[25]、工作载荷[26-27]和预紧载荷[28]等因素对摩擦力矩影响的规律。针对空间环境的特殊性，上述关于摩擦力矩研究中没有考虑环境温度影响结构参数、装配状况和预紧力，进而影响摩擦力矩。因此，有必要研究交变温度对航天轴承摩擦力矩的作用机理。

本文拟建立航天轴承摩擦力矩的数学模型，分析交变温度对摩擦力矩影响因素中的轴承结构参数、装配过盈量和预紧力的影响，进而揭示交变温度对轴承摩擦力矩的影响规律，并进行相应的试验验证。

1 轴承摩擦力矩数学模型

轴承摩擦力矩是指各种影响因素阻碍钢球运动的阻力矩。影响因素不仅有工艺因素和工况因素，还包含环境因素，如：环境温度、湿度、洁净度等。针对空间环境特殊性，沟道、钢球表面溅射MoS2，形成固体润滑膜。由于润滑方式不同，固体润滑和油脂润滑轴承的摩擦力矩机理也有差异。航天轴承摩擦力矩主要由弹性滞后摩擦力矩、差动摩擦力矩和自旋摩擦力矩组成[29]。

摩擦力矩阻碍钢球运动，因此需要分析接触区域内的运动和摩擦状况。根据接触理论，在载荷作用下，钢球与沟道的接触点扩展为接触椭圆。接触椭圆区域形状及其微区域的运动速度如图1所示。

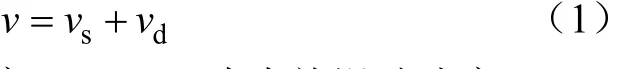
式中v为自旋滑动速度，m/s；vs为自旋滑动速度，m/s；vd为差动滑动速度，m/s。

图1 接触区域的滑动速度Fig.1 Slide velocity in contact area

由于载荷的差异，接触椭圆形状及内部的运动速度不同，且存在不同的运动区域，如图 2所示。在接触区域内，存在微滑区、纯滚动区和黏滞区。不同接触区域内的运动情况不同，形成不同形式的摩擦力矩。

图2 轴承接触区域分布Fig.2 Contact area distribution of bearing

1.1 弹性滞后引起的摩擦力矩

钢球在沟道内运动时，在接触压力的作用下导致材料弹性滞后，接触区前后两部分压力不对称对轴承产生摩擦力矩ME[30]。

式中Z为钢球数目；an为能量损失百分比；Qn为接触载荷，N。

1.2 差动滑动引起的摩擦力矩

钢球在沟道内运动时，接触椭圆内各点的线速度不同，钢球相对套圈微滑动，即差动滑动。差动滑动在内、外圈产生的差动摩擦力矩Mdi、Mdo分别为[29]

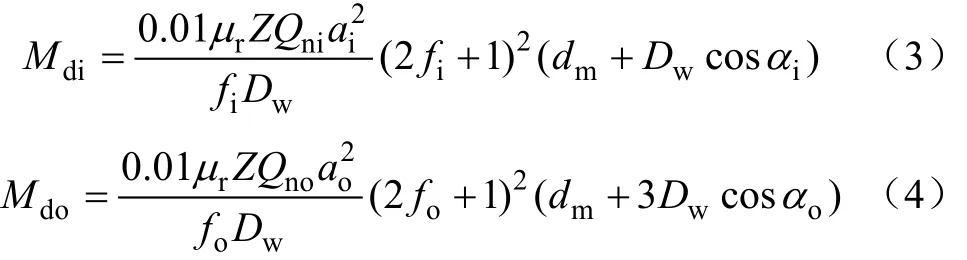
式中 fi、fo分别为内、外圈沟道曲率系数，Qni、Qno分别为内、外圈接触载荷，N；ai、ao分别为内、外圈接触椭圆长半轴，mm；αi、αo分别为内、外圈接触角，rad；μr为摩擦系数；dm为轴承节圆，mm；Dw为钢球直径，mm。

1.3 自旋滑动引起的摩擦力矩

钢球相对沟道表面椭圆接触区域的法向发生自旋运动，产生自旋摩擦力矩。自旋摩擦力矩Ms为[29]

式中E为第二类完全椭圆积分。

1.4 航天轴承摩擦力矩

由于航天轴承是固体润滑，则可以忽略内部的黏性摩擦力矩。在轻载状态下运转，航天轴承外圈沟道上的自旋运动小于内圈沟道，接近于“外沟道控制”状态[30]，则内、外圈处的摩擦力矩Mi、Mo可以表示为

式中MEi、MEo分别为内、外圈弹性滞后摩擦力矩，N·mm；Msi为内圈自旋摩擦力矩，N·mm。

综上所述，建立固体润滑轴承摩擦力矩的数学模型，为下文研究分析交变温度引起轴承结构参数、预紧力变化，进而影响摩擦力矩演变奠定理论基础。

2 交变温度对轴承摩擦力矩的影响

在空间环境中，环境温度在-60～80 ℃之间交替变化[31]，引起精密轴系产生热变形，进而导致航天轴承的装配过盈量和预紧力发生相应的变化，其中精密轴系组件如图3所示。

图3 精密轴系组件Fig.3 Components of precision shafting

2.1 交变温度对装配过盈量的影响

在交变温度作用下，主轴、轴承和轴承座都产生相应的热变形。由于各组件材料不同，导致轴承配合处的过盈量变化，如图 4所示。过盈量变化引起轴承结构参数的改变，进而影响航天轴承摩擦力矩。

设交变温度的变化量为ΔT，内圈和配合处主轴产生线性膨胀，热变形量Δds、ΔDi分别为

式中αs、αb为主轴和轴承的热膨胀系数，μm/℃；ds为主轴直径，mm；Di为内圈内径，mm。

同理，外圈和配合处轴承座也产生线性膨胀，热变形量 ΔDh、ΔDo分别为

式中 αh为轴承座的热膨胀系数，μm/℃；Dh为轴承座直径，mm；Do为外圈外径，mm。

由于配合处的公称直径相等，由变形协调关系可知，交变温度导致过盈量的变化量ΔIiT、ΔIoT分别为

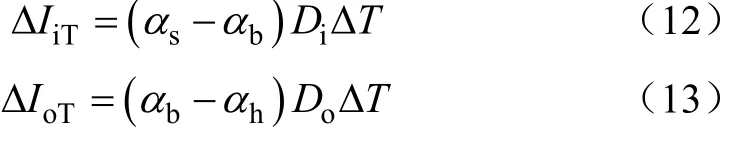
图4 装配示意图Fig.4 Schematic diagram of fitting

这里分析了交变温度影响轴承配合处过盈量变化，依据弹性力学可知过盈量引起轴承结构参数的变化量，为分析交变温度影响摩擦力矩奠定了基础。

2.2 交变温度对预紧力的影响

为了研究交变温度对航天轴承摩擦力矩的影响机理，需要建立预紧力随交变温度变化的数学模型。

在交变温度作用下，精密轴系组件不仅发生径向热变形，而且发生轴向热变形。各组件的热变形不同将引起钢球的压缩变形量发生相应的变化，即预紧力随交变温度变化而变化。

常温下，结合图2可知精密轴系组件中的主轴长度、轴承宽度和隔套长度间的几何关系为

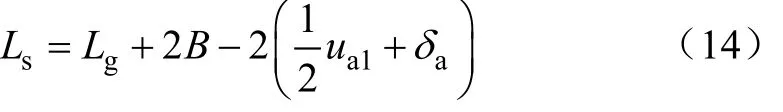
式中 Ls和 Lg为主轴和隔套长度，mm；B为轴承宽度，mm；δa为轴承轴向变形量，mm；ua1为装配后轴承轴向间隙，mm；。

交变温度作用下，航天轴承宽度 B、隔套长度Lg和主轴长度 Ls发生热变性，分别变为 B′、Lg′、Ls′。

式中αg为隔套的热膨胀系数，μm/℃。

环境温度变化后，主轴长度、轴承宽度和隔套长度间的几何关系为

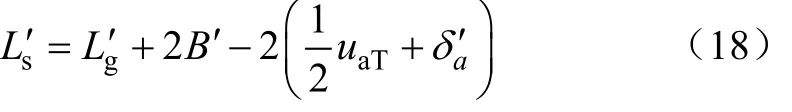
式中uaT、δa'为热变形后的轴向间隙和变形量，mm。

交变温度下，航天轴承发生热变形，其接触角与轴向变形量的关系为

式中BDw'为交变温度下的沟道曲率中心距离，mm；αT、αT'为交变温度下的初始接触角和预紧作用下接触角，rad。

交变温度下，预紧力与接触角的数学模型为

式中Kn为载荷-位移系数。

综合式(14)～(20)，得出交变温度下的预紧力。基于变形协调关系，获得了航天轴承预紧力随交变温度的演化机理。

综上所述，研究了交变温度对过盈量和预紧力的影响机理。在此基础上，结合摩擦力矩数学模型，分析交变温度引起过盈量和预紧力变化，进而得出交变温度影响摩擦力矩的作用机理。

3 摩擦力矩测试系统

基于上述交变温度对航天轴承摩擦力矩作用机理的理论分析，搭建摩擦力矩测试系统，借助高低温试验箱模拟空间环境的交变温度，测试交变温度对摩擦力矩的影响规律，进而验证理论分析的正确性。

3.1 摩擦力矩试验平台设计

摩擦力矩表现为阻碍钢球与套圈间相对运动的力矩。内圈在电机驱动下匀速旋转，钢球将相对内、外圈运动而产生摩擦力矩M，外圈在摩擦力矩M的作用下随之运转，而测量杆端受到约束力 F，则力 F产生的力矩等同于M，如图5所示。

图5 平衡力矩法示意图Fig.5 Method of balance moment

依据平衡力矩法自行研制了一台航天轴承摩擦力矩测试装置，搭建了如图 6所示的测试系统。主轴两端采用圆锥滚子轴承支撑，与步进电机通过联轴器连接，通过锁紧螺母对测试轴承施加轴向预紧力。拉压力传感器用于测试平衡摩擦力矩的拉力。测试系统采用两端支撑中间测量的方法，避免支撑轴承对测试轴承的影响，使得测量结果更加准确。测试装置中选用EVT-14C传感器，测试轴承的结构参数如表1所示，轴承材料为9Cr18，主轴材料为TC4R，其物理性能参数如表2所示。

图6 摩擦力矩测试系统Fig.6 Friction torque test system

3.2 交变温度对航天轴承摩擦力矩影响测试系统

为了测试交变温度对航天轴承摩擦力矩的影响规律，将摩擦力矩测试装置放置于高低温试验箱内。借助高低温试验箱模拟高低温及交变温度环境，摩擦力矩测试系统如图7所示。

在试验中，通过扭矩扳手施加轴向预紧力，研究预紧力对摩擦力矩的影响；借助高低温试验箱模拟交变温度环境，通过调节温度在-60～80 ℃范围内变化，获得交变温度对航天轴承摩擦力矩的影响规律，具体的试验流程如图8所示。

表1 角接触轴承几何参数(NSK71807C)Table 1 Geometric parameters of angular contact bearing(NSK71807C)

表2 轴承和主轴的物理性能参数Table 2 Physical property parameters of bearing and shaft

图7 交变温度下摩擦力矩测试系统Fig.7 Friction torque test system under alternating temperature

图8 摩擦力矩测试流程图Fig.8 Flow chart of friction torque test

4 试验结果分析

4.1 交变温度对轴承装配因素的影响

为探究交变温度对航天轴承摩擦力矩的影响机理，需要通过数值仿真和试验研究交变温度对摩擦力矩影响因素中过盈量、预紧力的作用，进而获得摩擦力矩演化规律。由于交变温度在-60～80 ℃和80～-60 ℃交替变化时，研究结果恰好相反，则交变温度选择了-60～80 ℃，具体交变温度对轴承装配因素的影响结果如图9所示。

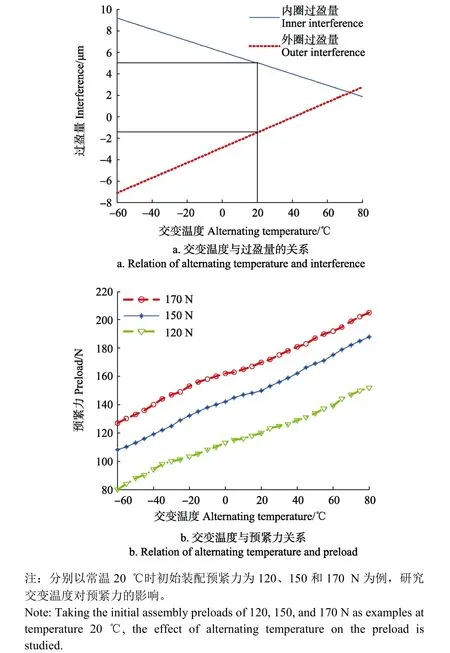
图9 交变温度与装配因素的关系Fig.9 Relation of alternating temperature and assembly factor

假设航天轴承在常温装配时，内、外圈初始过盈量分别为5和-1.5 μm。环境温度变化后，主轴、轴承座和轴承热变形不同，导致初始过盈量改变。由图9a所示变化规律可知：内、外圈过盈量与交变温度分别成反比和正比，增速分别为-0.05和0.07 μm/℃。轴承材料为9Cr18，主轴和轴承座的材料为 TC4，9Cr18的热膨胀系数大于TC4。

图9b为交变温度对轴承预紧力的影响规律。随交变温度升高，轴向预紧力增大，且预紧力的变化范围约为-40～40 N。精密轴系组件中的航天轴承是“背靠背”安装，温度升高时轴承轴向变形量增大，钢球压缩变形量增加，则预紧力变大。若轴向预紧力增加过大，则可能超出润滑膜的抗压极限；预紧力减小，精密轴系运转精度降低。

由上分析可知：在交变温度作用下，航天轴承在常温装配时的过盈量和预紧力发生改变，进而导致摩擦力矩发生变化。

4.2 影响因素与摩擦力矩的关系

上边分析了交变温度对航天轴承过盈量、预紧力影响，在此基础上分别研究摩擦力矩随过盈量、预紧力和温度的变化规律。通过数值仿真和试验研究过盈量、预紧力和温度对摩擦力矩的影响规律，并探究三者对摩擦力矩的影响效果，分析结果如图10所示。

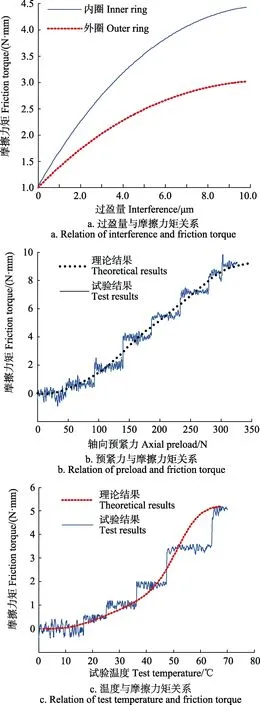
图10 影响因素与摩擦力矩的关系Fig.10 Relation of influencing factors and friction torque

图 10a为过盈量对轴承摩擦力矩的影响。由图 10a可知：随过盈量的增加，摩擦力矩增大，且内圈摩擦力矩增大量大于外圈，且约为 1.2～1.5倍。由于过盈量增大，径向间隙减小，摩擦力矩增大；内圈摩擦力矩由弹性滞后摩擦力矩、差动摩擦力矩和自旋摩擦力矩组成，而外圈摩擦力矩由弹性滞后摩擦力矩和差动摩擦力矩组成，所以内圈摩擦力矩增大大于外圈。

图10b为轴向预紧力与摩擦力矩的关系。在试验中，预紧力从0开始按50 N等量增加至350 N。预紧力增大，导致摩擦力矩随之增大，但摩擦力矩的增加量趋于减小。由于装配过盈量的误差，导致摩擦力矩理论和试验结果存在偏差。

在轴向预紧力为100 N时，试验温度对摩擦力矩的影响规律如图10c所示。在试验中，试验温度从0 ℃开始按10 ℃等量增加至80 ℃。摩擦力矩随温度升高而增大，且在高温时摩擦力矩变化速度明显增快。这是由于试验温度升高，轴承预紧力增大、内圈过盈量增大，则摩擦力矩也随试验温度升高而增大。

对比图10中10a、10b和10c可知：过盈量、预紧力和温度都与摩擦力矩正相关。对比这三者对摩擦力矩的影响，其中预紧力对摩擦力矩的影响效果最明显，温度次之，过盈量最弱。温度升高时，预紧力增大和内圈过盈量下降，摩擦力矩增大。说明预紧力增大引起摩擦力矩的增大量大于内圈过盈量下降引起摩擦力矩的减小量。温度引起摩擦力矩的变化量比预紧力引起摩擦力矩的变化量小，但是不可忽视的，因此环境温度对摩擦力矩的影响必须加以考虑。

4.3 交变温度对轴承摩擦力矩影响的试验分析

在测量交变温度对摩擦力矩的影响规律时，经过多次交变温度变化，测量摩擦力矩的变化，最终选取了第一周期和变化相同中的一个周期的变化曲线，结果如图11所示。交变温度升高，摩擦力矩增大；交变温度降低，摩擦力矩减小。在多次作用后，摩擦力矩的最大值小于初次最高温度下的摩擦力矩，摩擦力矩最小值大于初次最低温度下的摩擦力矩，最大值相差1.7 N·mm、最小值相差0.9 N·mm。摩擦力矩最大值变小反映的是精密轴系中航天轴承载荷的变小。

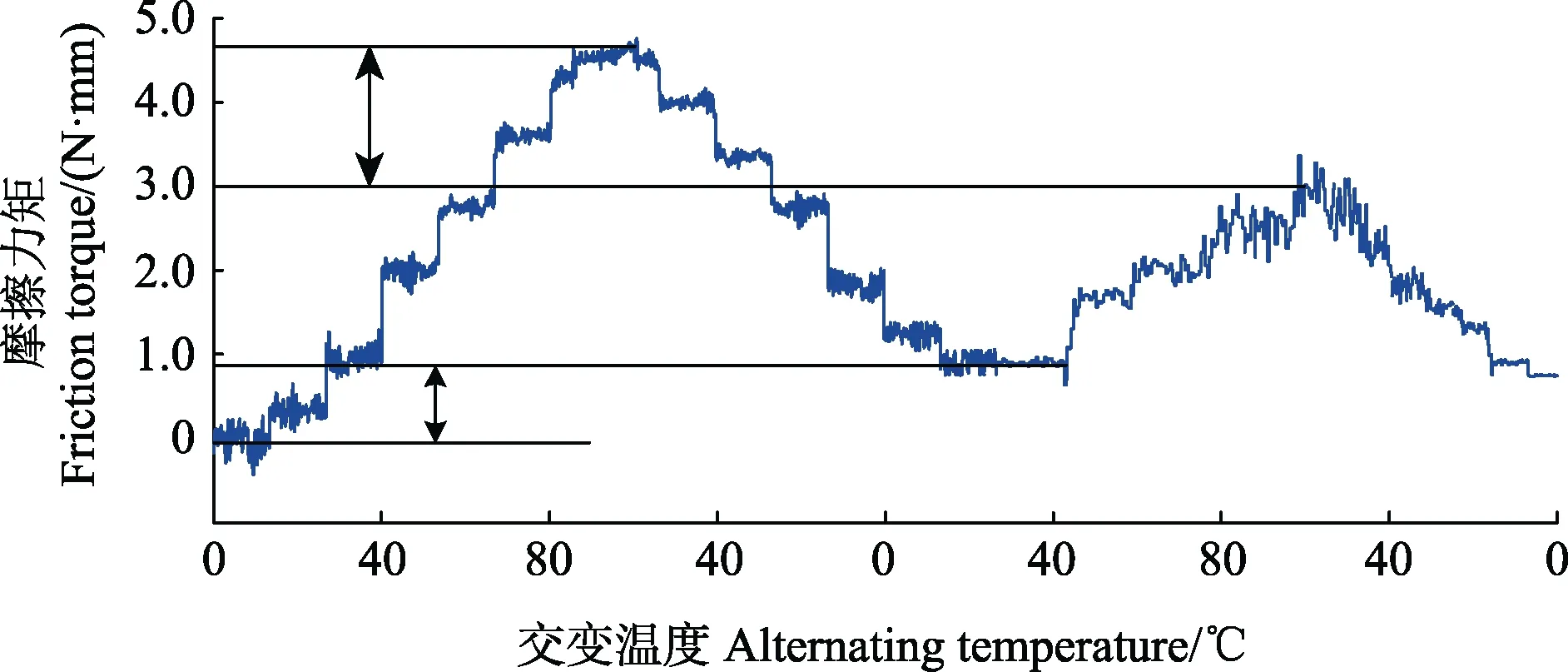
图11 交变温度对航天轴承摩擦力矩的影响Fig.11 Effect of alternating temperature on friction torque of aerospace bearings

5 结 论

本文通过理论和试验方法，分析了在-60～80 ℃内交变温度对精密轴系组件中航天轴承71807C摩擦力矩的影响，得出了以下的结论：

1) 环境温度升高时，内外圈过盈量增速分别为-0.05和0.07 μm/℃；在交变温度在-60～80 ℃变化时，预紧力随温度升高而增大，与常温时相比变化范围为-40～40 N。

2) 交变温度影响航天轴承的初始装配过盈量、预紧力，进而影响航天轴承摩擦力矩改变。

3) 航天轴承摩擦力矩随交变温度正变化，且与初始时刻相差的最大值和最小值分别为1.7和0.9 N·mm。

[参 考 文 献]

[1] 阎绍泽. 计及间隙的运动副和机械系统动力学的研究进展[J]. 北京大学学报：自然科学版, 2016, 52(4): 741－755.Yan Shaoze. Advances in modeling of clearance joints and dynamics of mechanical systems with clearances [J]. Acta Scientiarum Natualium Universitatis Pekinensis, 2016, 52(4):741－755. (in Chinese with English abstract).

[2] 刘庭伟，张宁，梁伟, 等. 星载活动部件用轴承的失效仿真分析及试验验证[J]. 中国机械工程，2014，25(21)：2864－2868.Liu Tingwei, Zhang Ning, Liang Wei, et al. Failure simulation analysis and experimental verification of bearings for spaceborne moving mechanism[J]. China Mechanical Engineering, 2014, 25(21): 2864－2868. (in Chinese with English abstract).

[3] Vanhulsel A, Velasco F, Jacobs R, et al. DLC solid lubricant coatings on ball bearings for space applications [J]. Tribology International, 2007, 40(7): 1186－1194.

[4] Singh H, Mutyala K C, Evans R D, et al. An investigation of material and tribological properties of Sb2O3/Au-doped MoS2solid lubricant films under sliding and rolling contact in different environments[J]. Surface and Coatings Technology,2015, 284: 281－289.

[5] Ning F, Yao J, Li R, et al. Research on the Mechanism of Alternating Temperatures on Space Bearing Preload[M].Mechanism and Machine Science. Springer, Singapore, 2017:597－608.

[6] 宁峰平，姚建涛，安静涛，等. 减缓空间机械臂热预紧力的研究[J]. 机械工程学报，2017，53(11)：54－60.Ning Fengping, Yao Jiantao, An Jingtao, et al. Research on mitigating the thermal preload of space manipulator[J].Journal of Mechanical Engineering, 2017, 53(11): 54－60.(in Chinese with English abstract).

[7] 古乐，聂重阳，郑德志，等. 空间环境回转-直线往复复合运动密珠轴系力载特性分析[J]. 机械工程学报，2016，52(7)：88－96.Gu Le, Nie Chongyang, Zheng Dezhi, et al. Analysis of load characteristics in linear bearing with shaft used in space environment for rotary-linear motion[J]. Journal of Mechanical Engineering, 2016, 52(7): 88－96. (in Chinese with English abstract)

[8] 徐志栋，杨伯原，李建华，等. 航天轴承在较高温度下摩擦力矩特性的试验研究[J]. 润滑与密封，2008，33(3)：66－68.Xu Zhidong, Yang Boyuan, Li Jianhua, et al. Experimental Research on friction torque characteristics of aerospace bearings in relative high temperature[J]. Lubrication Engineering, 2008, 33(3): 66－68. (in Chinese with English abstract)

[9] Lü M, Zheng F, Wang Q, et al. Friction and wear behaviors of carbon and aramid fibers reinforced polyimide composites in simulated space environment[J]. Tribology International,2015, 92: 246－254.

[10] Zhen J, Cheng J, Zhu S, et al. High-temperature tribological behavior of a nickel alloy matrix solid-lubricating composite under vacuum[J]. Tribology International, 2017, 110: 52－56.

[11] 宁峰平. 空间滚动轴承可靠性影响因素作用机理及其演化规律研究[D]. 秦皇岛：燕山大学，2015：17－35.Ning Fengping. Raseach on Mechanism and Evolution Law of Reliability Factors in Space Bearing[D]. Qinhuangdao:Yanshan University, 2015: 17－35. (in Chinese with English abstract).

[12] 安静涛. 空间角接触球轴承摩擦力矩理论分析及实验研究[D]. 秦皇岛：燕山大学，2016.An Jingtao. Theoretical Analysis and Experimental Study of Space Angle Contact Ball Bearing Friction Torque[D].Qinhuangdao: Yanshan University, 2016. (in Chinese with English abstract).

[13] Palmgren A. Ball and Roller Bearing Engineering[M].Burbank: Philadephia, 1959.

[14] Snare B. Rolling resistance in lightly loaded bearings [J]. The Ball Bearing Journal, 1968, 152: 3－8.

[15] Snare B. Rolling resistance in loaded roller bearings[J]. The Ball Bearing Journal, 1968, 153: 19－24.

[16] Snare B, Eng G. Rolling resistance in loaded ball contacts [J].The Ball Bearing Journal, 1968, 154: 3－14.

[17] 邓四二，李兴林，汪久根，等. 角接触球轴承摩擦力矩特性研究[J]. 机械工程学报，2011, 47(5)：114－120.Deng Sier, Li Xinglin, Wang Jiugen, et al. Frictional torque characteristic of angular contact ball bearings [J]. Journal of Mechanical Engineering, 2011, 47(5): 114－120. (in Chinese with English abstract)

[18] 邓四二，李兴林，汪久根，等. 角接触球轴承摩擦力矩波动性分析[J]. 机械工程学报，2011, 47(23)：104－112.Deng Sier, Li Xinglin, Wang Jiugen, et al. Analysis on the friction torque fluctuation of angular contact ball bearings [J].Journal of Mechanical Engineering, 2011, 47(23): 104－112.(in Chinese with English abstract)

[19] Gonçalves D, Cousseau T, Gama A, et al. Friction torque in thrust roller bearings lubricated with greases, their base oils and bleed-oils[J]. Tribology International, 2017, 107: 306－319.

[20] Ghanbari A, Khanmohamadi S. A new test rig for frictional torque measurement in ball bearings[J]. WSEAS Transactions on Systems, 2006, 5(9): 2172－21 77.

[21] 李佳琪，倪计民，石秀勇，等. 结构参数对增压器浮环轴承润滑特性和环速比的影响[J]. 农业工程学报，2017，33(2)：48－55.Li Jiaqi, Ni Jimin, Shi Xiuyong, et al. Effect of structural parameters on lubrication performance of floating ring bearing and ring speed ratio in turbocharger[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2017, 33(2): 48－55. (in Chinese with English abstract)

[22] Todd M J, Stevens K T. Frictional torque of angular contact ball bearings with different conformities conformities[R].Risley: Technical Report ESA-CR(P)-1221, 1978.

[23] 汤占岐，刘小君，逄明华，等. 脂润滑关节轴承的摩擦副表面织构设计及摩擦性能试验[J]. 农业工程学报，2016,32(12)：61－67.Tang Zhanqi, Liu Xiaojun, Pang Minghua, et al. Surface texturing design and frictional experiment of friction pair of grease lubricated spherical plain bearings[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2016, 32(12): 61－67. (in Chinese with English abstract)

[24] Bălan M R D, Stamate V C, Houpert L, et al. The influence of the lubricant viscosity on the rolling friction torque[J].Tribology International, 2014, 72: 1－12.

[25] Bhardwaj V, Pandey R K, Agarwal V K. Experimental investigations for tribo-dynamic behaviours of conventional and textured races ball bearings using fresh and MoS2blended greases[J]. Tribology International, 2017, 113: 149－168.

[26] Kitahara T, Okamoto J. Friction torque of instrument ball bearings under combined radial and thrust load[J]. Japan Society of Lubrication Engineers, Journal-International Edition, (ISSN 0389-5483), 1984 (5): 131－136.

[27] 夏新涛，樊雎，陈龙，等. 基于乏信息理论的转盘轴承启动摩擦力矩变异分析[J]. 农业工程学报，2012，28(增刊1)：81－86.Xia Xintao, Fan Ju, Chen Long, et al. Variation analysis of starting friction torque for slewing bearing based on poor information theory[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012,28(Supp.1): 81－86. (in Chinese with English abstract)

[28] 胡华君，潘博，孙京. 航天器驱动机构轴系摩擦力矩建模与分析研究[J]. 机械工程学报，2017，53(11)：75－80.Hu Huajun, Pan Bo, Sun Jing. Friction torque modeling of spacecraft driving mechanism shafting[J]. Journal of Mechanical Engineering, 2017, 53(11): 75－80. (in Chinese with English abstract)

[29] 宁峰平，姚建涛，孙锟，等. 多因素耦合对空间轴承热学特性的影响[J]. 浙江大学学报: 工学版，2016，50(1)：129－136.Ning Fengping, Yao Jiantao, Sun Kun, et al. Effect of multi-factor coupling on thermal properties of space bearing[J]. Journal of Zhejiang University: Engineering Edition, 2016, 50(1): 129－136. (in Chinese with English abstract)

[30] Jones A B. A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions[J]. Journal of Fluids Engineering, 1960, 82(2):309－320.

[31] 宁峰平，姚建涛，安静涛，等. 适应交变温度的空间轴承运行可靠性区域分析[J]. 机械工程学报，2015，51(15)：97－103.Ning Fengping, Yao Jiantao, An Jingtao, et al. Analysis of operational reliability region for space bearing in alternating temperature[J]. Journal of Mechanical Engineering, 2015,51(15): 97－103. (in Chinese with English abstract)