基于Voronoi模型的钽材料孔隙率与弹性模量辨识

，，

(1.广东工业大学 机电工程学院，广东 广州 510006；2.佛山诺威科技有限公司，广东 佛山 528225)

0 引言

高孔隙率三维开孔微结构多孔钽凭借其低弹性模量、通孔结构和良好的生物相容性等优越特性，在骨生物医疗领域有着重要的应用前景[1]。而如何构造与人体骨骼弹性模量相近的多孔钽模型，是多孔钽应用于骨生物医疗领域的关键所在。若植入体弹性模量过大，会对骨组织产生应力屏蔽效应，影响骨组织的正常发育，因此需获得不同孔隙率下钽的弹性模量。近年来，许多学者和专家对多孔模型的力学性能做了大量的理论分析和数值计算模拟工作。Vander Burg等[2]建立以规则胞体结构为基础的Voronoi随机模型。由于Voronoi随机模型可以较好的近似模拟实际微结构的三维空间结构，因此，大多数学者都是基于Voronoi随机模型来研究多孔材料的力学性能[3-4]。探讨了结构不规则的Voronoi随机模型对弹性性能的影响。卢子兴等[5]还利用随机模型计算了拉伸变形过程中的应力—应变曲线。Li等[6]对具有不规则胞孔和不同壁厚的蜂窝材料进行了动态性能模拟研究。上述研究多数模拟空间闭胞单元，采用壳单元构成有限元模型进行数值分析。而实际多孔钽微结构为开孔结构，由许多纵横交错的微杆件连接而成。

本文针对钽微结构特点，采用三维Voronoi随机分布模型，构造孔洞随机分布且相互连通的微结构模型，其结构与多孔钽微结构近似。微结构边界杆并采用梁单元，能更加精确模拟受载后的微结构的变形情况。为获得相同微结构下的不同孔隙率，在保持微结构单元中心不变的情况下，改变梁单元截面尺寸，调节模型的孔隙率。对不同孔隙率下的有限元模型进行准静态载荷作用下的有限元模拟分析，辨识不同孔隙率下的多孔钽与等效弹性模量之间的关系，并与实验结果对比，验证上述方法的精度。

1 模型的建立

1.1 多孔钽微结构构造

多孔钽微结构为三维开孔形态(图1)，空间结构为许多纵横杆件相互连接的形式，当制造工艺稳定时，各杆件直径大致相同。根据其结构特点，本文采用空间三维随机Voronoi方法。通过随机种子点(即孔洞)的分布，确定微结构形式[4]，原理图如图2所示。对比图1和图2两组图片可以看出两者在三维空间结构上均为通孔连杆结构，且孔洞大小都是随机分布，具有高度相似性。

图1 多孔钽微结构CT图片 图2 Voronoi构造模型

本文所采用工艺构造的多孔钽模型是用孔密度为40ppi海绵作为多孔钽3D打印的基体，并通过烧结获得最终模型，且烧结后模型会有30%的收缩。且根据实验数据结果得出，当模型边长的孔洞结构数量超过6个，整体模型的弹性模量趋于稳定。

结合Voronoi几何空间结构的构造原理和现有多孔钽的制作工艺。通过数学换算的关系推导出，利用Voronoi模型在5 mm×5 mm×5 mm的空间内随机生成1423个种子，可以构造出跟实际多孔钽接近的三维空间模型。

1.2 模型孔隙率计算

孔隙率，是指块状材料中孔隙体积与材料在自然状态下总体积的百分比，是微孔材料的重要表征参数。在本文的研究中，根据模型的实际结构特点先计算模型的实体体积所占比率，从而确定模型的孔隙率。模型实体所占比例，可以根据单元边的长度、及其直径，计算获得。根据模型的边界长度、杆件总长以及梁单元截面半径，可由式(1)计算出模型的孔隙率，式(2)可以根据给定孔隙率计算出对应梁单元所需设置的半径。

(1)

(2)

其中，S为模型孔隙率；l杆为杆件的总长度，mm；r为杆件横截面的半径，mm；a为模型的边长，mm。

图3和图4显示了在同一微结构下改变模型内部杆件的半径大小获得不同孔隙率模型的对比图。

图3 孔隙率为60%的模型 图4 孔隙率为90%的模型

1.3 等效弹性模量辨识

在生物骨修复体领域，修复体弹性模量必须跟骨组织的弹性模量接近，如若两者相差较大(一般情况是修复体弹性模量远大于骨组织弹性模量)，会产生应力屏蔽效应。使得骨组织受力减小，影响其正常生理环境，随着时间的推移会引来骨组织病变，甚至脆断等危险。所以辨识多孔模型的弹性模量显得尤为重要。

图5 弹性模量辨识原理图

本文对应多孔模型弹性模量辨识原理为：在图5所示的模型上表面施加正应力，测量模型上表面受力时向下的变形量。根据施加载荷、变形量以及模型结构尺寸，由(3)式计算等效弹性模量。

(3)

式中，E为模型等效弹性模量，Pa；FN为施加给模型的载荷力，N；L为模型的边长，m；Δl为模型的形变量，m；A为模型的等效横截面积，m2。

2 基于有限元仿真辨识

2.1 基体材料的设置

本文多孔钽模型的微孔结构为40ppi，但是在微结构连杆上，仍然存在尺度更小的微孔(孔径约为30 μm)。这些微孔使得钽径的弹性模量变小，根据钽CT扫描灰度信息，可测得其弹性模量约为70 GPa。故本文将此多孔模型基体材料的弹性模量设为70 GPa，泊松比0.3。

2.2 边界条件和载荷施加

图6 边界条件设置

在模型上表面中心位置取参考点，参考点与模型上表面设置接触为耦合，限定模型底面节点的自由度。最后在模型参考点处施加载荷大小为3 N，方向垂直向下的力，如图6所示。

2.3 仿真验证与结果分析

2.3.1 ABAQUS有限元仿真结果数据

根据前面有限元仿真分析，记录相同载荷不同孔隙率下模型的各项仿真结果数据。

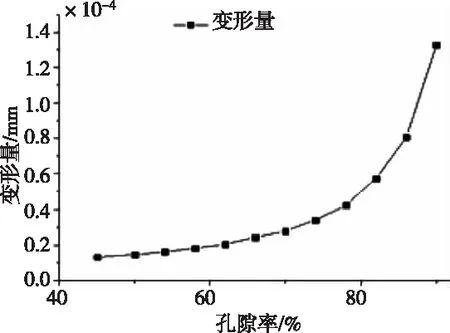
图7 模型孔隙率跟模型变形之间的关系图

1)孔隙率与变形关系

随着孔隙率增高，梁单元直径尺寸变小，受力更易弯曲，体现在模型上就是同等载荷下模型的形变量会增加，且高孔隙率下模型的型变量会急剧增加，如图7所示。

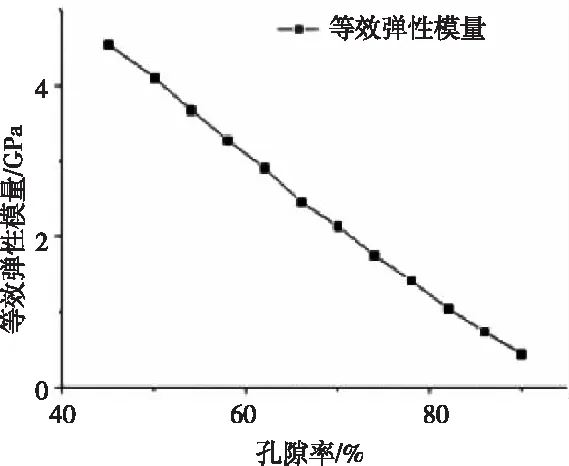
图8 模型孔隙率跟弹性模型之间的关系图

2)孔隙率与等效弹性模量关系

随着孔隙率增高，梁单元直径变小，受力更易变形。会使得模型的等效弹性模量减小，如图8。

2.3.2 孔隙率与弹性模量关系辨识

不同微结构的多孔模型，弹性模量与孔隙率具有不同的辨识公式。如具有随机结构的各种同向性闭孔泡沫材料，Christensen[7]已经给出了弹性模量预测公式。对14面体闭孔模型，Simone和Gibson[8]给出弹性模量拟合公式。Roberts和Garboczi[9]采用数字图像技术建立实体模型，计算拟合的弹性模量公式。

本文根据实体模型的结构特点，选取Roberts和Garboczi[9]以及卢子星[10]对弹性模量的拟合公式，公式形式：

(4)

通过仿真数据回归分析，计算得出：c=0.153，b=1.355代入公式得出模型孔隙率跟弹性模量关系为：

(5)

式中，s为模型孔隙率。

根据仿真结果以及公式的辨识结果，再对比试验数据(表1)。给出三者随孔隙率变化的关系图，如图9。可看出，模型在中等孔隙率为55%～65%的时候三者数值基本吻合。

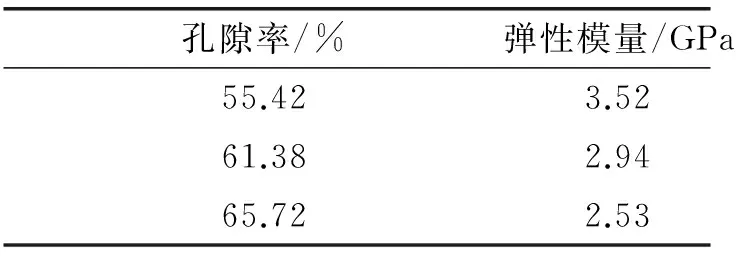
表1 孔隙率与弹性模量实验数据

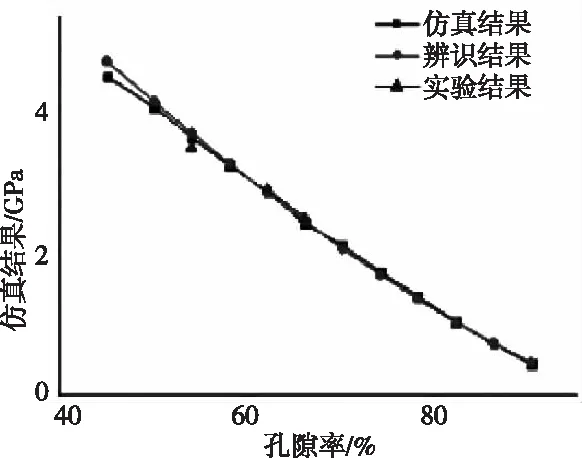
图9 各数据对比结果

2.3.3 误差分析

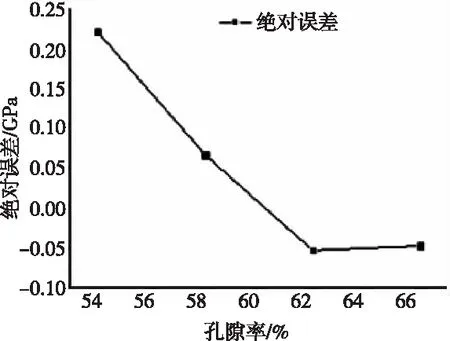
图10 辨识公式与实验结果的绝对误差

通过2.3.2得出的模型孔隙率跟弹性模量之间的辨识关系式。给定不同孔隙率，利用公式算出模型对应的等效弹性模量。对比实验结果跟公式辨识结果之间的绝对误差如图10。可以看出，在给定孔隙率为55%～65%实验结果下，辨识公式与实验结果的绝对误差不超过0.23 GPa，跟实验的结果基本一致，从而验证了实验结果的合理性。

3 讨论

本文主要探讨同一微结构下模型孔隙率跟等效弹性模量之间的关系。通过有限元力学分析，辨识不同孔隙率下多孔模型的等效弹性模量。通过对实验结果数据的分析，验证所辨识多孔模型等效弹性模量与孔隙率关系，与实验结果一致。

通过分析比较实验数据跟实际数据，此次研究结果发现模型在中等孔隙率的时候的辨识公式比较接近实际结果，可为多孔质模型的实体构造提供一定的科学依据。

[1] 陈长军，张超，王晓南，等.生物医用多孔钽制备工艺研究进展[J].热加工工艺，2014(4)：5-8.

[2] BURG MWDVD，SHULMEISTER V，GEISSEN EVD，et al On the linear elastic properties of regular and random open-cell foams models[J].Journal of Cellular Plastics，1997，33(1)：31-54.

[3] ZHU H X，HOBDELL J R，WINDLE A H.Effects of cell irregularity on the elastic properties of open-cell foams[J].Acta Mater，2000，48(20)：4893-4900.

[4] 袁应龙，卢子兴.利用随机模型计算低密度开孔泡沫材料的弹性模量[J].航空学报，2004，25(2)：130-132.

[5] 卢子兴，张家雷.开孔弹性泡沫材料拉伸变形过程的数值模拟[J].机械强度，2009，31(3)：432-436.

[6] LI K，GAO X L，SUBHASH G.Effects of shape and cell vall thickness variations on the elastic properties of two-dimensional cellular solids[J].International Journal of Solids and Structures，2005，42：1777-1795.

[7] CHRISTENSEN R M.Mechanics of low density materials[J].Journal of the Mechanics & Physics of Solids，1986，34(6)：563-578.

[8] SIMONE A E，Gibson L J.Effects of solid distribution on the stiffness and strength of metallic foams[J].Acta Mater，1998，46(6)：2139-2150.

[9] ROBERTS A P，GARBOCZI E J.Elastic moduli of model random three=dimensional closed-cell cellular solid[J].Acta Mater，2001，49，189-197.

[10] 王崇，卢子兴.闭孔Voronoi泡沫的弹性性能分析[J].航空学报，2007，28(3)：573-578.