建筑隔声测量不确定度及其在分级评价中的应用

蔡阳生，赵越喆

（1.福建工程学院 建筑与城乡规划学院,福州 350118；2.华南理工大学 亚热带建筑科学国家重点实验室，广州 510640）

建筑和建筑构件的隔声性能一般是用一组1/3倍频程或者1/1倍频程的隔声数据表示，体现了其对不同频带噪声的隔绝能力不同。GB/T 50121标准规定了将这一组数据转换成一个能代表所测对象隔声性能的单值量的方法，同时考虑了不同的频谱修正量，方便评价不同建筑和建筑构件的隔声性能，还规定了建筑和建筑构件隔声性能的分级方法[1]。在我国绿色建筑评价标准中，功能房间相关建筑构件的空气声隔声性能应满足现行国家标准《民用建筑隔声设计规范》GB 50118-2010中的低限值[2]，比如对分户墙的隔声性能要求为“计权隔声量+粉红噪声频谱修正量＞45 dB”。

在实际应用中，隔声测量存在分散性，即测量不确定度。这对于建筑工程商、建筑师和研究人员在确定建筑物和建筑构件是否满足上述标准要求或者比较不同产品的隔声性能时必须考虑的。如果这种不确定度在隔声测量中是确定的，则在隔声设计、测量以及评价阶段不需要加大隔声余量以保证工程完成后满足相关法律和标准的要求，而避免加大建造成本而产生浪费[3-4]。在我国，国家标准GB/T 19889.2规定了隔声测量数据的精密度的确定和应用方法，主要体现在重复性和再现性的应用[5]，但未规定评价一组隔声数据达到设计要求或者标准和法律规定的单值量时所对应的不确定度。因此有必要结合GB/T 50121标准和绿色建筑标准开展隔声单值量不确定度的研究。

Wittstock利用蒙特卡罗方法对1869组不同实验室间的复现性实验对比数据，统计分析得到一种计算一组隔声量数据的测量不确定度的方法，指出在计算不确定度时应考虑不同频率的隔声数据间的相关性，其研究结果还建议应采用全正相关不确定度进行评定，且考虑到小数点后一位数作为隔声单值量及其频率修正量的不确定度[6]。在该文的研究成果上，GB/T 19889.2的参考标准ISO 140-2更新为ISO 12999-1[7]。新标准采纳了Wittstock的上述建议。Jeffery Mahn采用相同的方法对加拿大国家研究委员会测量的200组石膏轻质结构的隔声数据进行研究，指出隔声单值量的不确定度与隔声量频率曲线的形状高度相关[8]。N.Garg研究了印度的建筑隔声材料的不确定度，其研究结果显示在阻尼控制区里较差的低频隔声性能对不确定度的影响很大[9]。在我国，亦有研究者开展了隔声的不确定度评定[10]，其是利用JJF1059.1-2012所规定的测量不确定度评定方法[11]对建立隔声单值量的分量不确定度评定模型，与ISO 12999-1所规定的方法不同。因此，本文拟根据ISO 12999-1所规定的隔声单值量不确定度方法对GB/T 50121规定的分级评价体系进行研究，以促进隔声量分级评价体系和绿色建筑中隔声评价方法的科学应用。

1 隔声单值量及其分级

隔声单值量的计算是将一组精确到0.1 dB的1/3倍频带的隔声量Ri与一组基准参考曲线Rref,i移动对比，且移动步长为1 dB，得到各频带的不利偏差之和

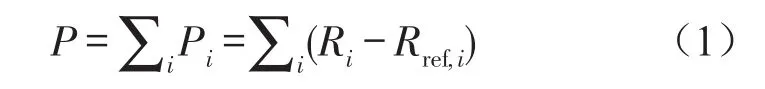
其中：i为频带序号，Rref,i为第i个1/3倍频带的空气声隔声基准值，Pi为第i个1/3倍频带的隔声量与对应频带的空气声隔声基准值的差值，称为不利偏差。要求该不利偏差之和尽量大，但不超过32.0 dB，此时参考曲线上的0 dB线（频率500 Hz）就是对应的空气声隔声单值量Rw。考虑到噪声的频谱特性，一般要在单值评价量上加上一频谱修正量C，该修正量由下式计算得出

上式可以改写成

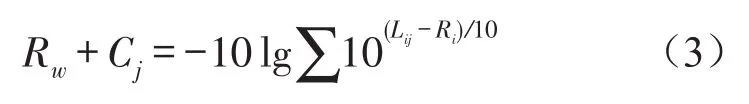
其中：j为频谱序号，j=1或2，1为计算C的频谱1（A计权粉红噪声），2为计算Ctr的频谱2（A计权交通噪声），Lij为第j号频谱计算频谱修正量的第i个频带的声压级，隔声单值量及频谱修正量在使用时应取整数。在国家标准GB/T 50121中，建筑构件的空气声隔声性能宜分成9个等级，每个等级单值量的范围应符合表1的规定。

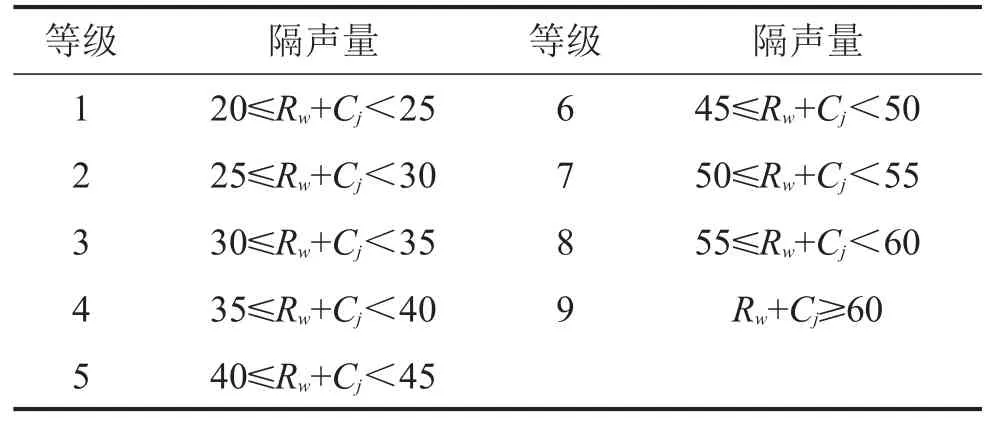
表1 建筑构件空气声隔声性能分级/dB

2 隔声单值量的不确定度

根据ISO 12999-1标准，不考虑该组1/3倍频带隔声量的相关性时，计权隔声量的不确定度称为非相关不确定度

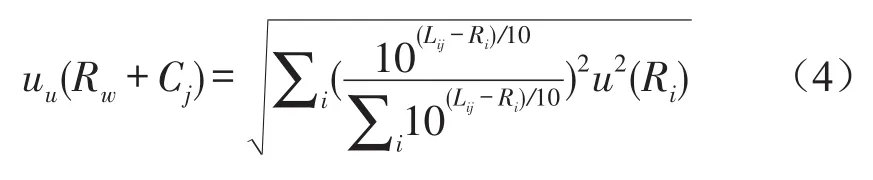
式中：u(Ri)为对应1/3倍频带的标准偏差。考虑该组1/3倍频带隔声量的相关性时，计权隔声量的不确定度需要由两次计算结果得出，第1次计算是1/3倍频带的隔声量加上每个1/3倍频带的不确定度，见式(5)。

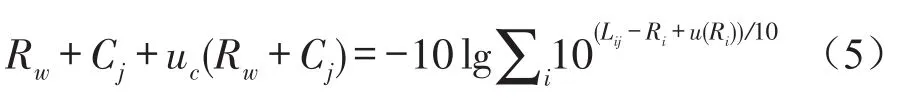
第2次计算是1/3倍频带的隔声量减去每个1/3倍频带的不确定度，见式(6)。

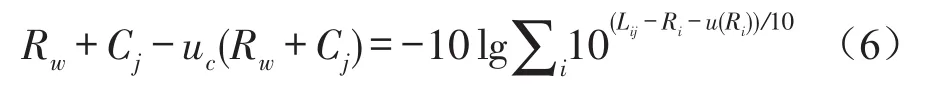
对式（5）和式（6）求和取平均，可得到计权隔声量的不确定度如式（7）所示，即全相关性不确定度。

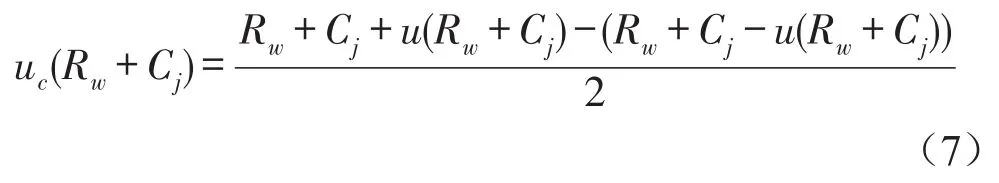
计算不带频谱修正的计权隔声量的不确定度时，只需要将式（5）至式（7）的Cj替换成其对应的参考频谱即可，且不确定度的结果取小数点后一位数。不同相关性且带不同频谱修正的计权隔声量的不确定度共有6个量，为了方便后续表达与分析，其含义及在本文中表示符号见表2。

表2 不确定度含义及符号

隔声单值量的测量不确定度主要受数据采集系统、声源室和接收室的声学特性、测量方法以及隔声频率特性等其他因素所决定[12]。

根据式（5）至式（7）计算的不确定度，再乘以包含因子，可得扩展不确定度如式（8）所示。

k为包含因子，由概率分布及置信水平所决定，当双边置信水平为68%(单边置信水平为84%)时，k=1[7]。如果要验证测量结果是否符合要求，则应用单边置信水平的包含因子来计算扩展不确定度U，并将该值加到最佳估计y（在隔声单值量不确定度评定时一般取计权隔声量）以检查测量结果是否满足要求。

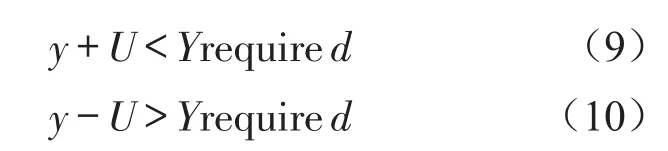
若满足式（9），则称该构件不满足隔声量要求；满足式（10），则称该构件满足隔声量要求。若式（9）和式（10）皆不满足的话，则需进行再次的独立测量方能给出是否符合要求的结论。

3 隔声单值量不确定度的分级应用

在国家标准GB/T 50121中，建筑构件空气声隔声性能的分级并没有考虑隔声量单值的不确定度，为此下面将使用ISO 12999-1标准[7]给出的普通频率范围（100 Hz～5 000 Hz）和扩展低频范围（50 Hz～5 000 Hz）的不确定度偏差计算。参考文献[13]中的30个建筑构件的隔声数据，这30个构件在一声源室（68 m3）和接收室（250 m3）组成的隔声室测量，测量声源为放在4个位置的独立扬声器系统，且在两个房间都有9个测量传声器位置。因此，尽管其声源室的容积较小，低频的扩散程度较差，但通过增加声源和传声器位置数量可在一定程度上改善其测量结果。这30个构件在频率范围50 Hz～5 000 Hz内的隔声量如图1所示。

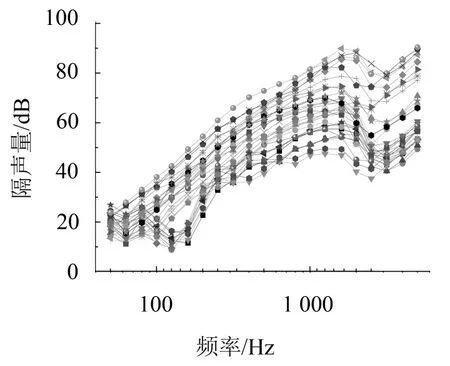
图1 建筑构件的隔声量

参考文献[13]中的序号及构件的计权隔声量如表3所示。未考虑频谱修正时的计权隔声量分布在表1中所示的第4等级到第9级，每个等级都有5个构件。采用扩展至50 Hz的低频范围，是因为低频隔声测量及评价越来越重要[14-15]。

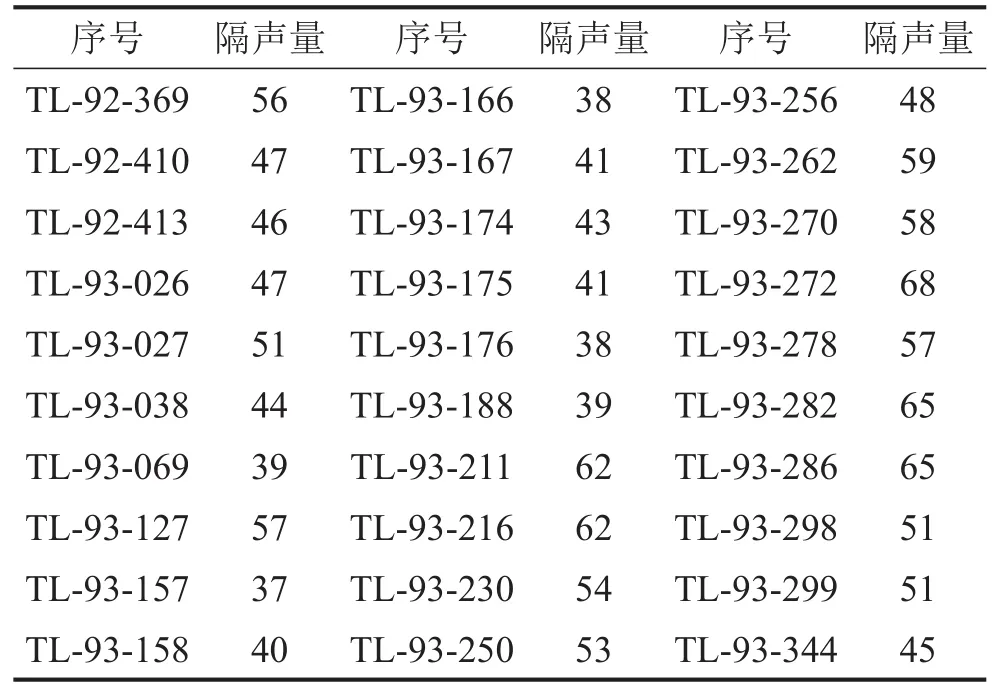
表3 构件的序号及其计权隔声量/dB

3.1 普通频率范围的不确定度

计算30个构件在普通频率范围的隔声单值量不确定度结果，如图2所示。可以看出：

(1)对于3种不同频谱修正的全正相关不确定度，uc,Ctr随计权隔声量的增加而加大，且变大的斜率最大，uc,c次之，uc最小；

(2)对于非相关不确定度，uu,Ctr也体现了随计权隔声量的增加而加大的规律，而uu,c和uu与计权隔声量的拟合直线方程的斜率是负的，即uu,c和uu不仅没有随计权隔声量的增加而加大，还略有减小；

(3)3种不同频谱修正的全正相关的不确定度皆大于对应的非相关不确定度。

3.2 扩展低频范围的不确定度

计算30个构件在扩展低频范围的隔声单值量不确定度的结果，如图3所示。

因为在扩展低频范围内未考虑频谱修正的计权隔声量，不需要计算50 Hz～80 Hz这3个频段的值，因此和普通频率范围的uu和uc完全相同。图3显示了一些跟图2相同的规律：

(1)对于3种不同频谱修正的全正相关不确定度，三者皆随计权隔声量的增加而加大，且uc,Ctr变大的斜率最大，uc,c次之，uc最小；

(2)对于非相关不确定度，uu,c和uu,Ctr体现了随计权隔声量的增加而加大的规律，而uu与计权隔声量的拟合直线方程的斜率是负的，即uu不仅没有随计权隔声量的增加而加大，还略有减小；

(3)3种不同频谱修正的全正相关的不确定度皆大于对应的非相关不确定度；

(4)不考虑频谱修正，普通频率范围和扩展低频范围的隔声单值量不确定度相同，这是因为计算隔声单值量只考虑100 Hz～3 150 Hz频率范围的隔声量。

图3与图2不同的结果包括：

(1)对于全正相关的不确定度，扩展低频范围的uc,c和uc,Ctr随计权隔声量的增加而增加的斜率较普通频率范围的大；

(2)无论是考虑生活噪声频谱还是交通噪声频谱修正的隔声单值量，扩展低频范围的不确定度会随计权隔声量的增大而显著增大，而普通频率范围的不确定度随计权隔声量的增大而发生的变化并不那么显著。

3.3 不确定度个例分析及应用

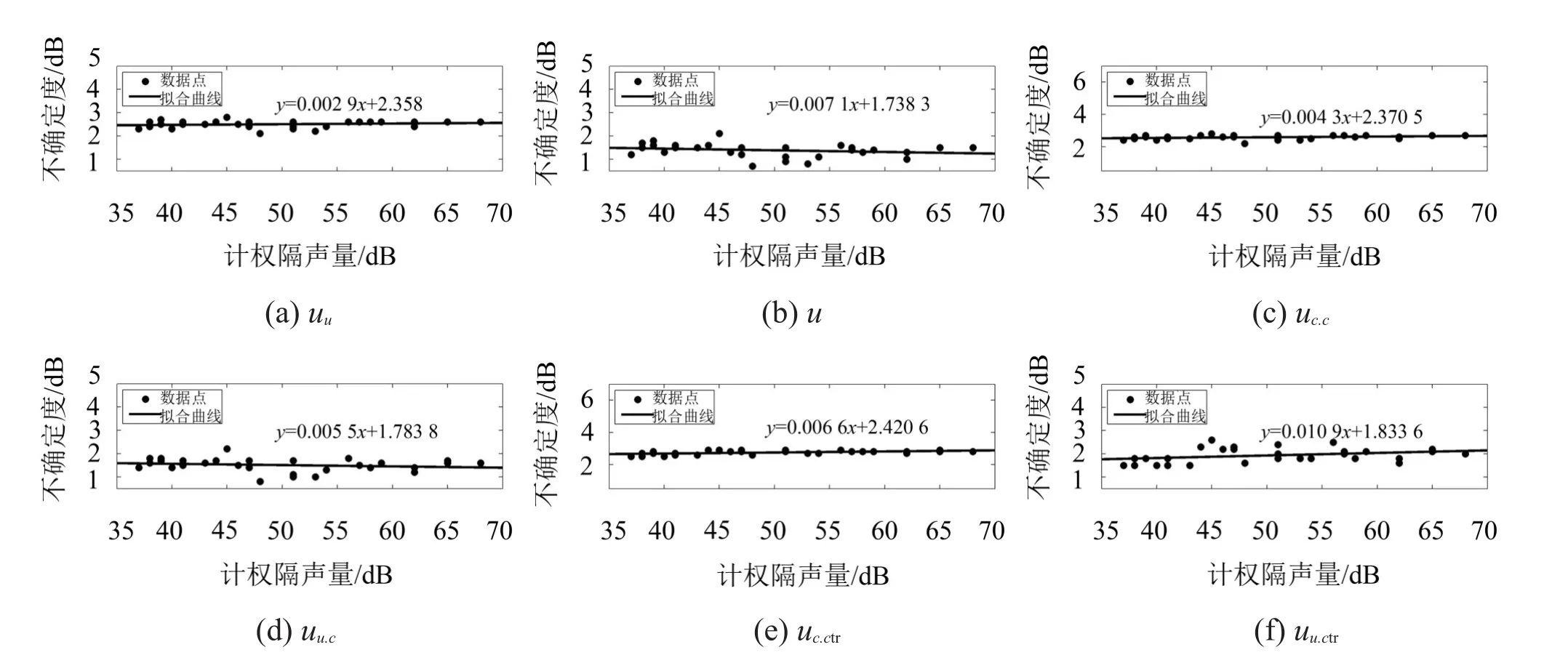
图2 普通测量频率范围的不确定度

图3 扩展低频范围的不确定度

尽管大部分构件的分析结果都体现了图2和图3的规律，但仍有个别构件由于其频谱特性的原因，体现出比较有意思的不确定度。以构件TL-93-344和TL-93-216为例，其不确定度和隔声量分别如表4和图4所示，TL-93-344的计权隔声量RW(C；Ctr；C50-3150；Ctr,50-3150)=45(-7；-15；-7；-18)dB，TL-93-216 的计权隔声量RW(C；Ctr；C50-3150；Ctr,50-3150)=62(-3；-10；-8；-21)dB，可以看出，虽然TL-93-216的计权隔声量比TL-93-344大，但是其在普通频率范围内的不确定度却比TL-93-344小；且在未考虑频率修正时，无论是在普通频率范围内，还是考虑到扩展频率范围的TL-93-216的不确定度都比TL-93-344小。这个与图2、图3所显示的规律不一样。从图4可以看出，TL-93-344在低频范围受阻尼控制作用有一个“低谷”，而高频范围受吻合作用产生的“低谷”较TL-93-216的大，这是其产生较大的不确定度的原因。

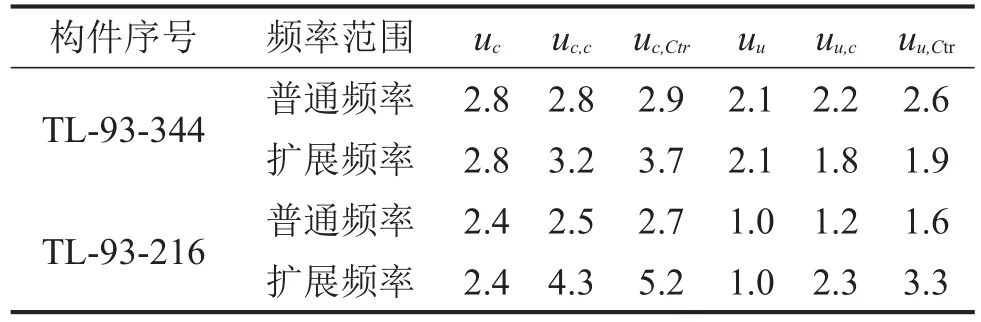
表4 两个构件的不确定度

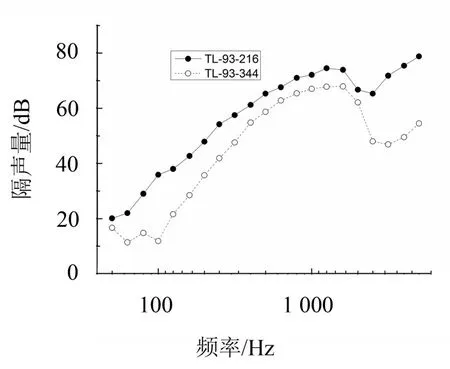
图4 两个构件的隔声量

不确定度对于建筑构件隔声性能的分级也有较大影响。以构件TL-93-344为例，若不考虑不确定度，此时RW(C；Ctr；C50-3150；Ctr,50-3150)=45.6(-6.3；-14.4；-6.5；-17.4)，即RW＋C为39.3 dB，满足4级隔声性能，RW＋Ctr为31.2 dB，满足3级隔声性能，RW＋C50-3150为39.1 dB，满足4级隔声性能，RW＋Ctr,50-3150为28.2 dB，满足2级隔声性能。若考虑不确定度，根据ISO 12999-1的建议采用全正相关不确定度，则有RW＋C－U为36.5 dB，满足4级隔声性能，RW＋Ctr－U为28.3 dB，满足2级隔声性能，RW＋C50-3150－U为35.9 dB，满足3级隔声性能，RW＋Ctr,50-3150－U为24.5 dB，满足1级隔声性能。可见考虑了不确定度后，同一构件的隔声性所能满足的等级较不考虑不确定度时低，若进一步考虑频谱修正量后，隔声性能等级下降更为厉害，这是因为轻质结构的低频性能较弱从而产生较大的不确定度所引起的。

利用不确定度可以明确建筑构件满足某个等级的隔声要求，也可以明确其不满足某个等级的隔声要求。还是以构件TL-93-344为例，如RW＋C＋U为42.1 dB，小于45.0 dB，即不满足6级隔声性能，亦不满足绿色建筑评价标准对分户墙的隔声量要求。同理，RW＋Ctr＋U为34.1 dB，不满足4级隔声性能，RW＋C50-3150＋U为42.3 dB，不满足6级隔声性能，RW＋Ctr,50-3150＋U为31.9 dB，不满足4级隔声性能。可见考虑了不确定度后，建筑构件的隔声性能往往会落在一个评价区间，且不确定度越大，该区间越大，要确定建筑和建筑构件的隔声性能等级则越困难。

4 结语

评价建筑和建筑构件的隔声性能是否达到某一个级别或者是否满足规范所要求的隔声量，并非直接评价其计权隔声量是否达到相关要求，而是需要考虑其隔声单值量的不确定度。本文根据ISO 12999-1所规定的隔声单值量不确定度方法计算30个构件的隔声单值量不确定度，并结合GB/T 50121规定的分级评价体系进行分析，结果表明：

(1)对于3种不同频谱修正的全正相关不确定度，三者皆随计权隔声量的增加而加大，且uc,Ctr变大的斜率最大，uc,c次之，uc最小，特别是在扩展低频围时，这种斜率的差异会更明显，这与建筑构件在低频范围的隔声性能较弱有关；

(2)若构件在低频范围和高频范围分别受阻尼控制作用和吻合作用而产生“低谷”，则其隔声单值量不确定度会比较大；

(3)考虑了测量不确定度后，建筑构件的隔声性能往往会落在一个评价区间，该区间为不确定度的两倍，该区间越大，要确定建筑和建筑构件的隔声性能等级越困难。在不确定度较大时，建筑构件的隔声性能可能会落在几个不同的隔声等级中，这在GB/T 50121的分级评价体系中未体现出来，也未在绿色建筑评价标准中体现出来。因此在我国加快推进建筑和建筑构件的隔声单值量不确定度评定的应用，不仅有助于建筑隔声评价的科学应用，也可以推进绿色建筑的隔声性能评价应用，更有助于国际上对我国隔声实验室的测量结果的认可以及基于“一带一路”的产能输出。

参考文献：

[1]GB/T 50121-2005.建筑隔声评价标准[S].北京：中国标准出版社，2005.

[2]GB/T 50378-2014.绿色建筑评价标准[S].北京：中国建筑工业出版社，2014.

[3]GARG N,SAXENA T K,KUMAR A,et al.Uncertainty evaluation and implications of spectrum adaption terms in determining the airborne sound insulation in building elements[J].Noise Control Engineering Journal,2014,62(5):333-343.

[4]GARG N,MAJI S.On analyzing the correlations and implications ofsingle-numberquantities forrating airborne sound insulation in the frequency range 50 Hz to 5 kHz[J].BuildingAcoustics,2015,22(1):29-44..

[5]GB/T 19889.2-2005.声学-建筑和建筑构件隔声测量-第2部分：精密度的确定、验证和应用[S].2005.

[6]WITTSTOCK V.On the uncertainty of single-number quantities for rating airborne sound insulation[J].Acta Acustica united withAcustica,2007,93(3):375-386.

[7]ISO 12999-1.Acoustics－Determination and application of measurement uncertainties in building acoustics－Part 1:Sound insulation.Geneva:International Organization for Standardization,2014.

[8]MAHN J,PEARSE J.The uncertainty of the proposed single number ratings for airborne sound insulation[J].BuildingAcoustics,2012,19(3):145-172.

[9]GARG N,KUMAR A,MAJI S.Measurement uncertainty in airborne sound insulation and single-number quantities:Strategy and implementation in Indian scenario[J].MAPAN,2016,31(1):43-55.

[10]邱立凡，席亦农，周庆去.空气声隔声量测量不确定度的分析与评定[C].中国造船工程学会船舶力学学术委员会水下噪声学组成立三十周年船舶水下噪声学术讨论会，2015：544-552.

[11]JJF 1059.1-2012.规程测量不确定度评定与表示[S].北京：中国标准出版社，2013.

[12]WITTSTOCK V.Determination ofmeasurement uncertainties in building acoustics by interlaboratory tests.Part 1:Airborne sound insulation[J].Acta Acustica united withAcustica,2015,101(1):88-98.

[13]R E HALLIWELL,T R T NIGHTINGALE,A C C WARNOCK,et al.Gypsum board walls:transmission loss data[R].NRC ReportNo.IRC-IR-761(1998).

[14]PEDERSEN D B,ROLAND J,RAABE G,et al.Measurement of the low-frequency sound insulation of building components[J].Acta Acustica united with Acustica,2000,86(3):495-505.

[15]ZHENG W,LEI Y,HUANG Q,et al.Improving low frequency performance of double-wall structure using piezoelectric transducer/loudspeaker shunt damping technologies[J].Journal of Low Frequency Noise,Vibration andActive Control,2012,31(3):175-192.