减速带及发动机联合激励下车辆混沌识别与智能抑制
2018-05-11胡启国王宇谦
胡启国,韩 奥,王宇谦
(重庆交通大学 机电与车辆工程学院,重庆 400074)
连续型减速带被设置在高速公路的一些特殊路段,其原理是使通过的车辆产生振动,提示驾驶员减速[1]。在连续型减速带的周期性激励下,非线性悬架车辆有可能产生混沌现象。混沌有可能对车辆造成不良影响,对车辆混沌状态的识别和抑制十分重要。
国内外学者对车辆的非线性特性做了诸多研究。G Litak等利用Melnikov过程分析了单自由度车辆模型在白噪声路面激励下进入混沌的途径[2]。Q Zhu等对车辆在正弦路面激励下的混沌状态进行分析,发现车辆在某激励频率区间内存在混沌[3]。DNaik等建立了包含时间延迟和速度反馈的单自由度汽车模型,发现恰当确定延迟时间能够有效消除车辆混沌[4]。杨绍普等利用随机Melnikov过程分析车辆在随机路面激励下路面白噪声强度对车辆混沌状态的影响,研究表明噪声强度越大,车辆混沌越不容易发生[5]。梁山等采用仿真和实验的方法研究了二自由度1/4车辆非线性悬架模型的混沌振动特性,运用频率分岔图、相轨迹图等图像揭示了车辆在连续型路面激励下产生混沌的可能性,并引入直接变量反馈控制将车辆的混沌运动转化为周期运动[6-7]。
尽管国内外学者对车辆混沌做了诸多研究,相关研究仍存在待改进之处。在车辆模型建立方面,未考虑到发动机对车辆混沌的影响;在车辆混沌识别方面,频率分岔图、相轨迹图等图像仅能定性分析车辆混沌状态,在车辆混沌识别时具有一定主观性;在车辆混沌抑制方面,利用反馈控制抑制车辆混沌时,反馈增益系数对车辆混沌抑制效果有明显影响,利用传统方法确定最佳反馈增益系数较为困难。故文中建立考虑发动机激励的五自由度车辆模型,以车辆系统最大Lyapunov指数衡量车辆混沌程度,引入粒子群算法搜索反馈控制的最佳反馈增益系数,提高最佳反馈增益系数的搜索效率,优化反馈控制对车辆混沌的抑制效果。
1 连续型减速带路面激励模型
以半正弦函数建立减速带模型,减速带高度为h,单个减速带宽度为w1,各减速带间隔为w2,且w1=w2=w。减速带静态模型如图1所示。减速带高度h=0.005 m,减速带宽度w1=0.5 m,减速带间隔w2=0.5 m。
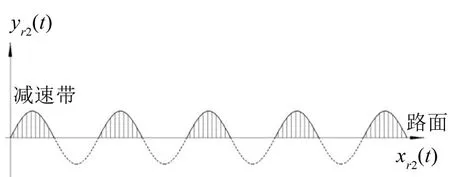
图1 减速带静态模型
汽车以速度v通过减速带,通过单个减速带所需时间为t1,t1=w1/v。通过减速带间距所需时间为t2,t2=w2/v,由于w1=w2,故t1=t2。车辆以速度v通过一个减速带和一个减速带间距的时间,即连续型正弦减速带动态模型的周期T

根据式(1)可得该动态模型的角速度

则连续型正弦减速带的动态模型为

2 非线性汽车悬架模型
车辆结构复杂,需要根据一定规则做相应简化。考虑到车辆在通过减速带时两侧路面激励基本相同,前后轮处路面激励存在相位差,将车辆视为左右对称结构,建立考虑发动机激励的五自由度1/2车辆模型,如图2所示。
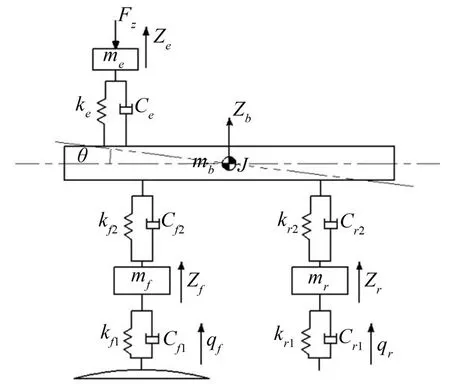
图2 五自由度车辆模型
图2中ze为发动机的垂直位移;zb为车身的垂直位移;zf、zr分别为前、后悬架的垂直位移;qf、qr分别为前、后轮胎的垂直路面激励。me为发动机质量;mb为车身质量;mf、mr为前、后轮胎质量。a、b分别为前后悬架到质心的距离;d为发动机悬置装置位置到质心的距离。ke为发动机悬置装置弹簧刚度;kf2、kr2分别为前、后悬架弹簧刚度;kf1、kr1分别为前、后轮胎的弹性刚度。ce为发动机悬置装置阻尼系数;cf2、cr2分别为前、后悬架阻尼系数;cf1、cr1分别为前、后轮胎的阻尼系数。文中符号e表示发动机,f表示前,r表示后,1表示车轮,2表示悬架。
以车辆静止时的平衡位置为各广义坐标系的坐标原点,车辆的运动方程可以表示为

非线性弹簧的弹性力可表示为
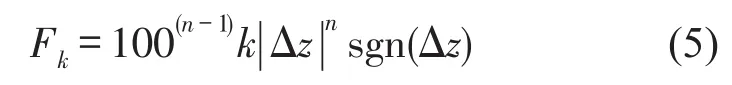
式(5)中Fk为弹性力;k为弹性系数;Δz表示弹性形变量;sgn(·)为符号函数,表示正负。当n=1时弹簧表现为线性,n≠1时弹簧表现为非线性。
悬架阻尼器和轮胎的阻尼力可表示为

式中cu为压缩行程阻尼,cd为拉伸行程阻尼。
发动机激励可以表示为[8]
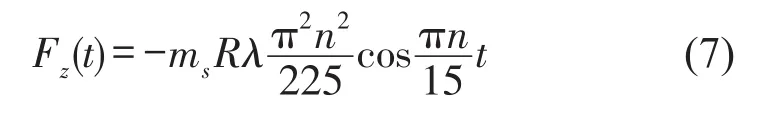
车辆模型参数如表1所示[9]。
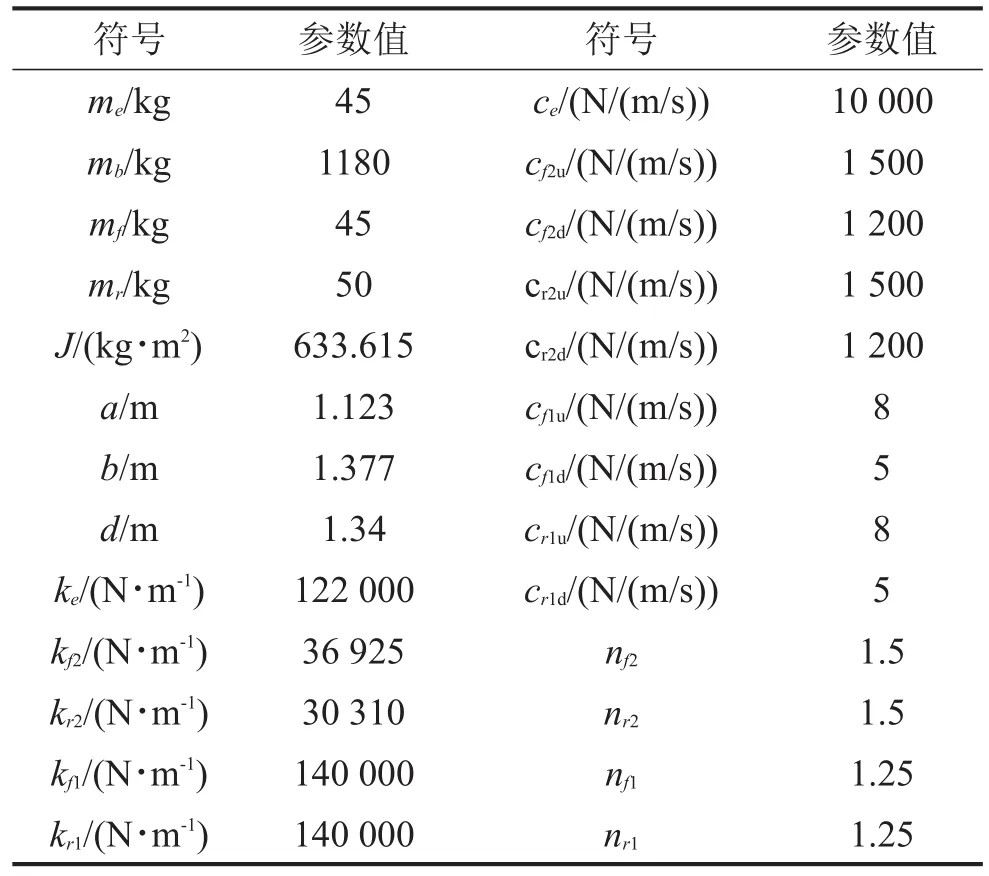
表1 汽车模型参数
3 车辆混沌特性分析
3.1 基于图像法的混沌特性分析
一般车辆通过连续型减速带的速度范围为10 m/s~20 m/s。以车速为横坐标,以各车速工况下车身位移的poincaré截面点作为纵坐标,绘制车身位移的车速分岔图,如图3所示。
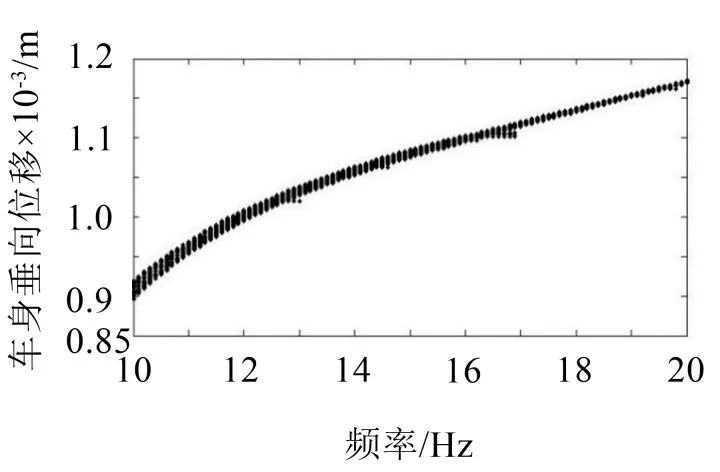
图3 车辆垂向位移频率分岔图
分岔图不能有效分辨各车速工况下准周期运动和非周期运动,车辆系统的混沌状态和进入混沌的途径需要利用poincaré截面图做进一步分析。对于poincare截面,以在该平面上的一个相点为起点,相轨迹经过一周期运动后又回到该平面,相轨迹与该平面的交点为poincare截面点。当经过多个周期后,该截面上点的个数反映了系统的运动状态。当Poincare截面上只有一个不动点和少数离散点时,可判定运动是周期的;当Poincare截面上是一封闭曲线时,可判定运动是准周期的;当Poincare截面上出现成片的密集点,且有层次结构时,可判定运动处于混沌状态。选取三个车速为10 m/s、15 m/s和20 m/s,分别作对应车速工况下车身的poincaré截面图如图4、图5和图6所示。分析低速、中速和高速工况下车辆混沌状况和车辆进入混沌的途径。
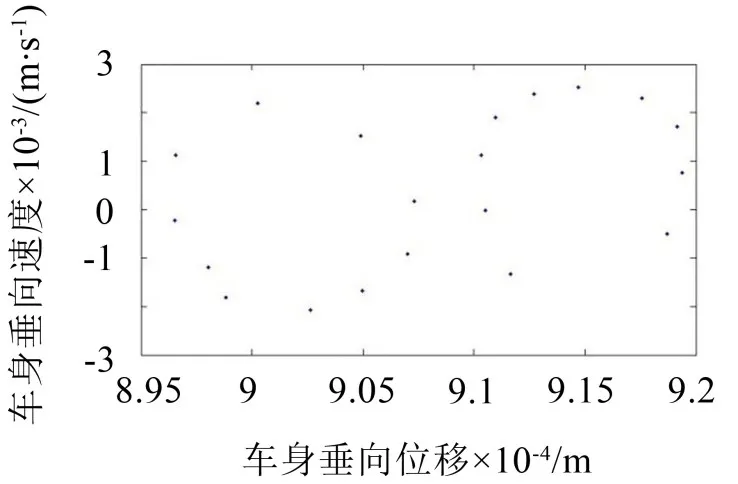
图4 10 m/s车速工况下车身poincaré截面图
图4中车身poincaré截面点组成两个相互分离的极限环,表明车辆处于非周期运动状态,车辆进入混沌的途径为多激励频率下系统振动的相互耦合。
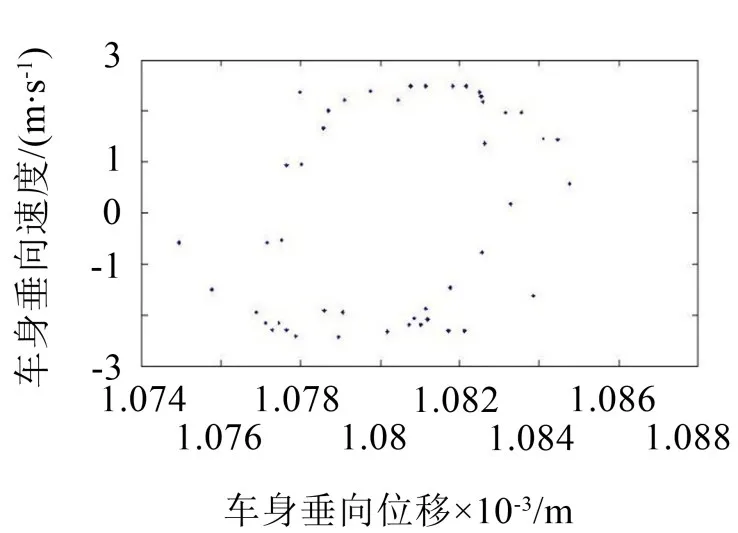
图5 15 m/s车速工况下车身poincaré截面图
图5中车身poincaré截面点的两个相互分离的极限环融合为一个极限环且有破裂的趋势,表明车辆处于非周期运动状态,车辆进入混沌的途径仍为多激励频率下系统振动的相互耦合。
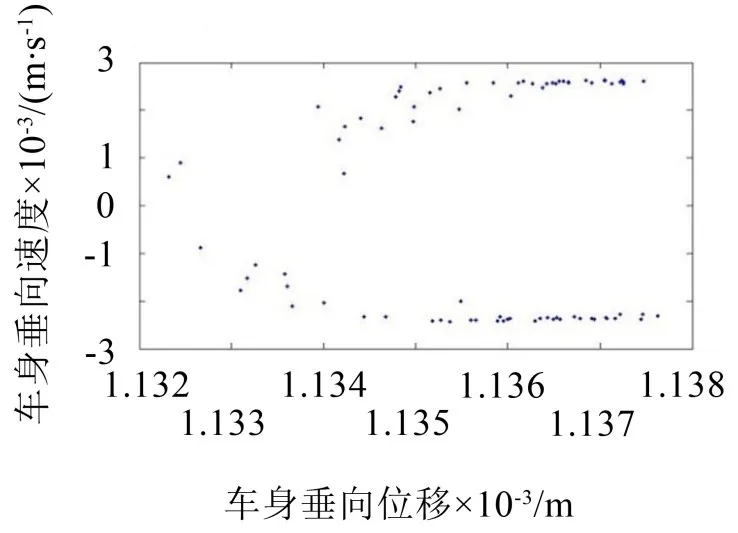
图6 20 m/s车速工况下车身poincaré截面图
图6中车辆相轨迹图为一组螺旋线,poincaré截面图中极限环完全破裂,表明车辆处于非周期运动状态,极限环破裂,车辆由分岔途径进入混沌。
3.2 基于数值法的混沌特性分析
利用车辆系统最大Lyapunov指数识别车辆系统的混沌状态,Lyapunov指数是目前定量识别混沌最可靠的一个指标[6],表示相空间内邻近轨迹的平均指数发散率的数值特征,体现了混沌系统对初值的敏感性。
以4阶5级龙格库塔算法求解式(4),得到一组时间序列,将此时间序列做标准化处理后首尾相接组成一组一维时间序列。利用坐标延迟法对该时间序列进行相空间重构
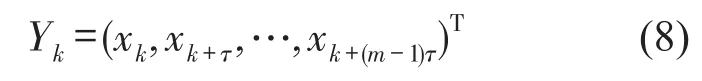
式(8)中Yk为m维相空间,k=1,2,…,N-(m-1)τ,τ为延迟时间,m为嵌入维数,为保证相空间重构的保真度和Lyapunov指数计算的准确性,这两个参数的选取十分重要,采用互信息法得到延迟时间τ与信息熵I(τ)的关系[10],得到的结论是最佳延迟时间为向后延迟14个采样点,采样补偿T=0.001即延迟时间为τ=0.014 s。利用虚假邻近点法确定嵌入维数,利用matlab计算出嵌入维数与虚假临近点占比的关系,可以得出的结论是当嵌入维数为m=29时,继续扩大嵌入维数,虚假临近点占比不再发生改变,故路面激励频率为10 Hz时,车辆系统时间序列的嵌入维数应该取29[10]。再利用wolf法计算相空间重构后时间序列的最大Lyapunov指数,各车速工况下车辆系统最大Lyapunov指数如图7所示。

图7 各车速工况下车辆系统最大Lyapunov指数图
各车速工况下车辆最大Lyapunov指数均大于零,车辆处于混沌状态。低速时路面激励频率与发动机激励频率相差较大,在多频率激励下车辆混沌较为明显;中速时路面激励频率与发动机频率相差减小,车辆极限环逐渐融合,车辆混沌程度降低;高速时车辆极限环破裂,车辆由分岔途径进入混沌,混沌程度急剧增大。注意到在15.69 m/s车速工况下,车辆系统最大Lyapunov指数剧烈增大,这是由于在此车速附近车辆极限环完全融合,车辆进入混沌的途径由多频率激励转变为分岔,此时车辆发生阵发性混沌。
4 车辆混沌智能抑制
4.1 反馈控制
直接变量反馈控制[7]能够在系统目标非稳定周期轨道未知的前提下,通过调节反馈增益系数实现混沌抑制。利用分段二次函数x|x|作为反馈控制的形式,这种控制方法易于实现,对系统影响小[11]。设计系统的控制器为U=Kx|x|的形式,其中K为反馈增益系数矩阵,将控制器作用于原系统,令
则系统前4项的状态空间方程可根据式(4)改写为
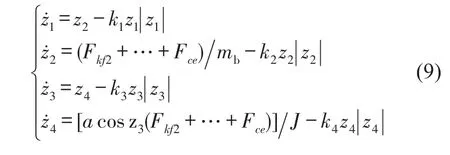
4.2 最优反馈控制系数智能搜索
反馈增益系数决定了混沌抑制的效果,引入改进的粒子群算法,以使车辆系统最大Lyapunov指数最小化为控制目标,搜索最佳反馈增益系数[k1,k2,k3,k4]。与传统反馈控制不同,文中反馈增益系数在控制过程中不断变化,扩展了粒子群算法的搜索域,可以得到更佳的反馈控制效果。同时,为了避免粒子群算法中普遍存在的“早熟”问题,还需要对粒子群做“早熟”判断,利用混沌搜索对“早熟”粒子群做早熟处理,避免计算陷入局部最优解。
搜寻全局最优反馈系数[k1,k2,k3,k4]步骤如下:
(1)初始化M个4×N的随机向量组成一个(P×4)×N的矩阵作为初始解,生成同构随机向量作为初始粒子群的“迁移”速度。
(2)以反馈控制后车辆系统最大Lyapunov指数作为相应粒子群的适应度,第i代粒子群适应度记为Lyai。Lyaig为第i代粒子群中最小的最大Lyapunov指数,对应的反馈系数即为局部最优反馈系数kig;Lyaq为迄今为止搜索到的最小的最大Lyapunov指数,对应的反馈系数即为全局最优反馈系数kq。
(3)若反馈控制后车辆最大Lyapunov指数为非正数或到达极限代数,则结束计算,将该粒子群位置作为全局最优解输出;若不满足此条件,则进行早熟判断。
(4)粒子群群体适应度方差σ2体现了粒子群的“聚集”程度,以σ2为粒子群早熟判据,其定义为
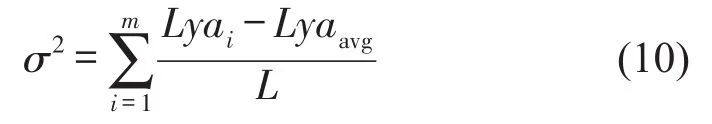
式中m为目前为止粒子群代数,Lyaavg为目前为止粒子群平均适应度,L为归一化标定因子,限制了群体适应度方差的大小,其确定公式为
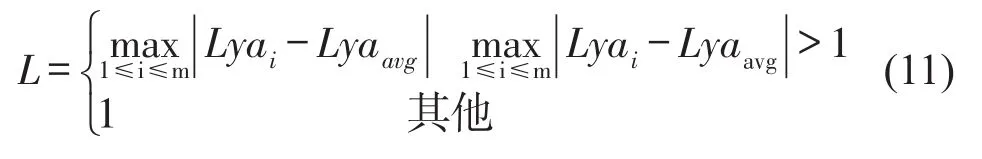
当σ2<C时,认为粒子群处于早熟状态,做早熟处理;当σ2>C时,认为粒子群处于非早熟状态,则产生下一代粒子群,将产生的下一代粒子群返回步骤(3)继续粒子群计算。文中将此常数C设置为0.7。
(5)混沌优化算法利用混沌变量的随机性、遍历性和规律性特点在解空间中进行优化搜索,易于跳出局部最优解[12]。选择Logistic映射产生混沌变量

其中:μ是控制参数,当μ=4时Logistics系统处于完全混沌状态。利用混沌对初始条件的敏感性选取n个有微小差别的初值yq,由式(12)得到n个混沌变量yp′。根据式(13)产生n个新的反馈增益系数kigq′。
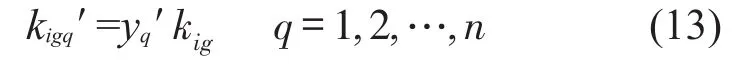
这n个变量组成混沌优化算法的解空间,将这n个新的反馈增益系数代入式(13)计算车辆系统的最大Lyapunov指数,此解空间内使车辆系统最大Lyapunov指数最小的反馈增益系数记为kig′,以kig′更新kig并返回步骤3继续粒子群计算。
(6)根据式(14)和式(15)生成第i代粒子群及其“迁移”速度
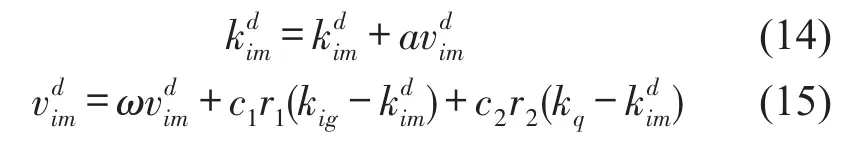
其中:i=1,2,3,4;d=1,2,…,M;a为约束系数,控制了粒子群“迁移”速度的权重;ω≥0为惯性因子;c1、c2≥0为学习因子;r1、r2为随机因子,为[0,1]之间的随机数。
其流程如图8所示。

图8 改进粒子群算法流程图
4.3 控制效果分析
为分析反馈控制的混沌抑制效果,将利用粒子群算法搜索得到的全局最优反馈增益系数代入式(9)中,做控制后车速为20 m/s时车身poincaré截面图,如图9所示。
比较图6与图9,发现控制后车辆运动状态由混沌运动转化为周期运动。反馈控制能够有效抑制车辆系统混沌。

图9 20 m/s车速工况下控制后车身poincaré截面图
进一步分析反馈控制在各车速工况下对车辆混沌的抑制效果,计算反馈控制后各车速工况下车辆系统最大Lyapunov指数,反馈控制前后车辆系统最大Lyapunov指数如图10所示。
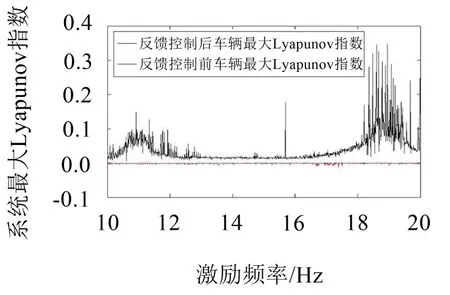
图10 反馈控制前后各车速工况下车辆系统最大Lyapunov指数图
各车速工况下车辆系统最大Lyapunov指数均有明显减小,说明各车速工况下反馈控制均能有效抑制车辆混沌。
5 结语
建立考虑发动机振动的五自由度汽车模型,分析车辆在连续型减速带及发动机联合激励下的混沌特性,并以基于粒子群算法的反馈控制对车辆混沌进行智能抑制,得到如下结论:
(1)在减速带与发动机联合激励下,车辆在10 m/s~20 m/s车速范围内均处于混沌状态。车速在中低速范围内车辆进入混沌的途径是多频率激励下系统振动的耦合;高速时车辆由分岔途径进入混沌。
(2)由车辆各车速工况下最大Lyapunov指数可知,低速时路面激励频率与发动机激励频率相差较大,在多频率激励下车辆混沌较为明显;中速时路面激励频率与发动机频率相差减小,车辆极限环逐渐融合,车辆混沌程度降低;高速时车辆极限环破裂,车辆由分岔途径进入混沌,混沌程度急剧增大;在15.69 m/s车速工况下,车辆系统最大Lyapunov指数剧烈增大,在此车速附近车辆极限环完全融合,车辆进入混沌的途径由多频率激励转化为分岔,车辆发生阵发性混沌。
(3)利用反馈控制抑制车辆混沌,引入粒子群算法搜索反馈控制的全局最优反馈增益系数,并利用混沌搜索对粒子群算法做出改进,避免粒子群发生“早熟”现象,使计算尽快跳出局部最优解。结果表明在各车速工况下该反馈控制均能有效减小车辆系统最大Lyapunov指数,抑制车辆混沌,将车辆运动状态由混沌运动转化为周期或准周期运动。
参考文献:
[1]李灿,李韶华,黄宏伟.道路连续减速带对重载汽车平顺性影响[J].动力学与控制学报,2012(3):273-277.
[2]LITAK G,BOROWIEC M.Nonlinear vibration of a quarter-car model excited by the road surface profile[J].Communications in Nonlinear Science&Numerical Simulation,2006,13(7):1373-1383.
[3]ZHU Q,ISHITOBI M.Chaotic vibration of a nonlinear full-vehicle model[J].International Journal of Solids&Structures,2006,43(3):747-759.
[4]NAIK R D,SINGRU P M.Resonance,stability and chaotic vibration of a quarter-car vehicle model with timedelay feedback[J].Communications in Nonlinear Science&Numerical Simulation,2011,16(8):3397-3410.
[5]杨绍普,李韶华,郭文武.随机激励滞后非线性汽车悬架系统的混沌运动[J].振动、测试与诊断,2005,25(1):22-25.
[6]梁山,郑剑,朱勤,等.非线性车辆模型混沌振动的仿真与实验研究[J].机械强度,2012,34(1):6-12.
[7]郑剑,梁山,朱勤,等.路面连续减速带下汽车悬架的混沌振动分析[J].公路交通科技,2011,28(1):132-137.
[8]潘云伟.基于粒子群算法的悬架参数优化及联合激励作用下的汽车振动研究[D].重庆:重庆交通大学,2014:32-35.
[9]郑剑.减速带激励下非线性汽车悬架系统动力学特性研究[D].重庆:重庆大学,2010:24-25.
[10]韩奥.基于连续型减速带及发动机激励下车辆系统混沌识别及智能抑制[D].重庆:重庆交通大学,2017.
[11]蔡明山.永磁同步电动机中混沌运动的非线性反馈控制[J].武汉理工大学学报,2008,30(4):149-151.
[12]魏玉琴,戴永寿,张亚南,等.基于Tent映射的自适应混沌嵌入式粒子群算法[J].计算机工程与应用,2013,49(10):45-49.
