结合EMD与DWT-ACF的语音基音周期检测改进算法

张 涛，章小兵，朱明星

(安徽工业大学 电气与信息工程学院，安徽 马鞍山 243002)

基音周期检测是语音信号处理中的重要步骤之一，它在语音识别、语音情感识别、语音合成以及语音编码中有着广泛的应用[1]。于是，精准的基音周期检测就具有非常重要的意义。目前的基音周期检测方法有自相关函数法(Auto Correlation Function，ACF)[2]、平均幅度差函数法(Average Magnitude Difference Function，AMDF)[3]、倒谱法[4]、线性预测系数(Linear Prediction Coefficient，LPC)[5]、小波变换[6]以及相衍生的小波加权自相关函数法[7-8]、平均幅度差自相关函数法[9]等。由于语音是一种复杂非平稳的信号，受限于人的声道、基音周期范围、情感以及单词的音调等各种因素的影响，因此基音周期的精确检测实际上是非常困难的，但基于基音在语音识别过程中的重要性，人们提出了各种基音周期检测算法。而这些方法中自相关函数法(Auto Correlation Function，ACF)即使在完全纯净语音下也会发生基音的倍频和半频错误，平均幅度差函数法(Average Magnitude Difference Function，A-MDF)在信号幅度变化较快时会出现均值下降的趋势，倒谱法对噪声比较敏感，当遇到受噪声污染的语音时其检测误差会显著上升[3-4]。由此看出，不同的基音周期检测方法都有各自的优缺点，它们在复杂的语音下并不完善，因此探索一种精确的基音周期检测方法就显得尤为重要。

本文针对传统的小波-自相关法(DWT-ACF)[10]的缺点提出了一种基于经验模式分解(EMD)[11]下改进小波-自相关的基音周期检测算法。该算法先利用经验模式分解(EMD)处理含噪语音信号，提取基本模式分量IMF3－IMF6以消除含噪信号部分噪声以及消除趋势，改善自相关函数法在基音的倍频和半频上的错误（在语音信号中提取基频常用的自相关方法中，倍频和半频是常见的错误。前者是那些低的第1共振峰的干扰；后者出自个人的发音习惯导致的奇数周期和偶数周期的声门脉冲的强度的固有变化。这是由语音信号的特性造成的，与汉语‘上声’结尾有些人发出的吱嘎声，基频很低，难以测量，有同样的性质。这类错误即使在信噪比很高的条件下也会出现。因为言语中基频是一个有规律的慢变过程），以及小波法的基音定位偏差[9]，再结合小波算法抗噪声性能与自相关函数法的简单精准，得出一种精确定位基音周期的新算法(EMDDWT-ACF)。对EMDDWT-ACF算法进行仿真实验，实验结果表明，该方法提取的语音基音周期基音轨迹平滑，且相对应的基音频率能与实际的基音频率很好吻合。

1 EMD算法基本原理

1998年，Norden E.Huang等对非平稳信号在瞬时频率方面进行深入研究，创造性地提出了本征模式函数(Intrinsic Mode Function，IMF)[12]以及将任意信号分解为IMF的经验模式分解(Empirical Mode Decomposition，EMD)。

为了得到有意义的瞬时频率，提出了基本模式分量(IMF)的概念，基本模式分量的提出需要满足两个基本条件：

(1)在语音数据序列中，极值点的个数Ne与过零点的个数Ns要满足

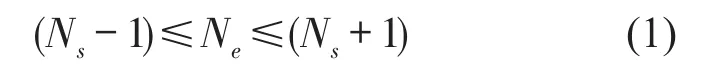
(2)在任意时间点ti上，信号局部极大值确定的上包络线gmax(ti)与局部极小值确定的下包络线gmin(ti)均值为零，即

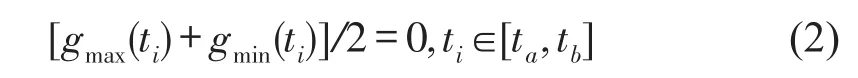
其中：[ta,tb]为语音数据段所在的时间区间。

用验模式分解(EMD)将信号的基本模式分量(imf)提取出来，然后对其分析，这是一个筛选过程，其分解原理如下：

(1)将原始信号的x(t)的所有局部极值点分别用3次样条曲线连接起来，使信号的所有数据点都处于这两条包络线之间，定义上、下包络线均值组成的序列为m(t)。

(2)从原始信号x(t)中减去m(t)，得到

检测h1(t)是否满足IMF的两个基本条件，若不满足，把h1(t)作为待处理信号，重复式(3)，直到找到一个h1(t)是一个基本模式分量，记为

(3)得到一个基本模式分量后，从原始信号x(t)中减去c1(t)，得到剩余值序列r1(t)

(4)将r1(t)作为新的原始信号重复上述步骤得到各阶IMF分量，记为c1(t)、c2(t)、...、cn(t)，直到满足预先设定的停止准则，则停止，最后剩下一个余项为rn(t)。

该方法的核心思想是将原始信号x(t)分解为若干基本模式分量ci(t)和一个剩余分量rn(t)，见式(6)

具体分解结果见图1，对一段纯净语音进行EMD分解，得到各阶imf分量。

图1 EMD分解

从图1中可以看出，对纯净语音进行EMD分解后，得到的各阶imf分量中imf1到imf6包含语音信号的大部分信息，imf6之后的分量主要是语音趋势分量。

1.1 EMD语音增强

对原始纯洁语音x(t)进行加噪得加噪语音信号x′(t)，对其进行EMD分解得到一系列基本模式分量imfi，丢掉前 2阶模态分量 imf1、imf2，再重构新的信号x̂(t)

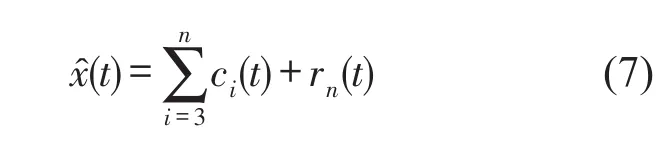
根据文献[13]提出的方法，EMD分解后的前两阶imf含有高斯白噪声75%的分量和噪声的共振峰，实验中丢弃了前两阶imf相当于对带噪语音信号进行语音增强处理，但是丢弃的两阶imf中同时也包含语音信号的成分，但这并不影响后续的基音周期检测，见图2。

从图2(a)中可见对纯洁语音进行重构imf3之后的信号可以保留大部分语音信号，而图2(b)为对加噪语音进行重构imf3之后的分量，可以明显看出已去除大部分噪声，且信噪比SNR从5提升到8.56，足见算法的效果。

1.2 语音消除趋势

通过对EMD分解后的imf分析可知，经过EMD分解处理后的语音信号，其imfj（这里的j针对实验的语音设定为6）之后的分量以及残余分量，大多都是低频分量，这些信号包含语音的趋势，并不能反应语音的特性，但这些信号中的低频噪声和工频对语音的基音周期检测又会产生较大的影响，它会干扰到基音周期算法的准确率。故本算法对减噪后的信号进行重构，再进行EMD 2次分解，分解后得到新的cj(t)和剩余分量rm(t)，试验中丢弃c7(t)之后分量以及剩余分量，再次重构得到新处理后的信号f(t)为

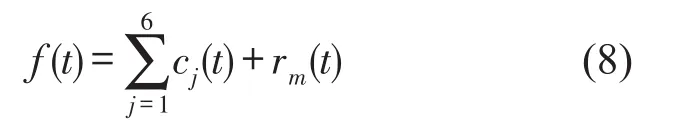
第1次分解和第2次分解是分开进行的，第1次分解后重构的信号用来检测元音主体。在元音主体的检测之前是要进行能熵比端点检测，这里选用能熵比端点检测而没选择其他类型的端点检测是由于在一般的端点检测中，为了检测出一些语音的头、尾，经常将检测条件设置稍宽一些，但是语音头、尾部并不具有声带振动那样的周期性，也就检测不到相应的基音，而本算法设置的能熵相比端点检测条件较为严格，与传统的双门限不同的是本文设置用一个门限阈值Ti作为判断，判断能熵比值是否大于Ti，把大于Ti的部分作为有话段的候选值，再进一步判断该段长度是否大于给定的判定最小值miniL，只有大于最小值的段才能作为有话段。

本文并不是采用对各元素进行分割方法得到元音主体，而是在能熵比端点检测判定出有话段后，在每个有话段中寻找能熵比的最大值Emax，设置比例系数r2，使得阈值T2=Emax×r2，这样对于不同的有话段就有不同的T2值，然后把能熵比大于T2的部分作为元音主体部分。

第2次分解后重构得到的信号是用来优化小波算法的，详细过程见下一小节。

2 改进的EMD小波-自相关函数法

2.1 基于EMD的小波算法

小波变换是一个平方可积函数f(t)（对应本文经过EMD处理后的信号f(t)）与一个在时频域上具有良好局部性质的小波函数φ(t)的内积

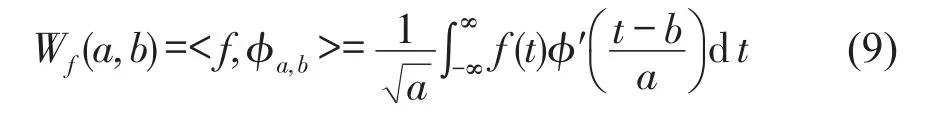
式中：＜f，φa,b＞表示两函数的内积；a＞0为尺度因子；b为位移因子；φ′(t)表示表示小波函数φ(t)的复数共轭。

实际应用中的小波几乎都是离散的，本文使用二进离散小波，故对尺度因子a和位移因子b进行离散得：a=2m，b=n2m

离散小波函数为

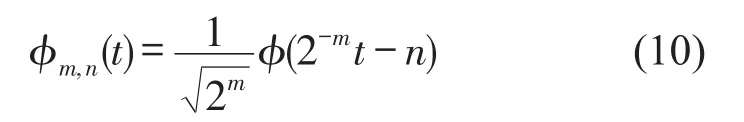
对应的EMD 2次重构后的语音信号f(t)的DWT可以表示为

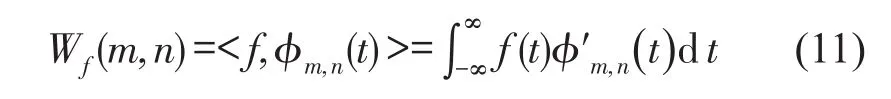
对f(t)进行分帧加窗，取来一帧浊音信号进行小波变换，然后用upcoef函数对小波处理的语音低频系数进行重构，得到重构后的信号x′i(n)。

糯福乡有“绿色宝石”之美誉，绿色、生态、民族、边疆是糯福的鲜明特点。全乡辖9个村民委员会，91个村民小组，有国土面积879.67平方公里，占全县总面积的1/10，是澜沧县国土面积第三大乡。耕地52147亩，其中：水田14185亩，旱地37692亩。

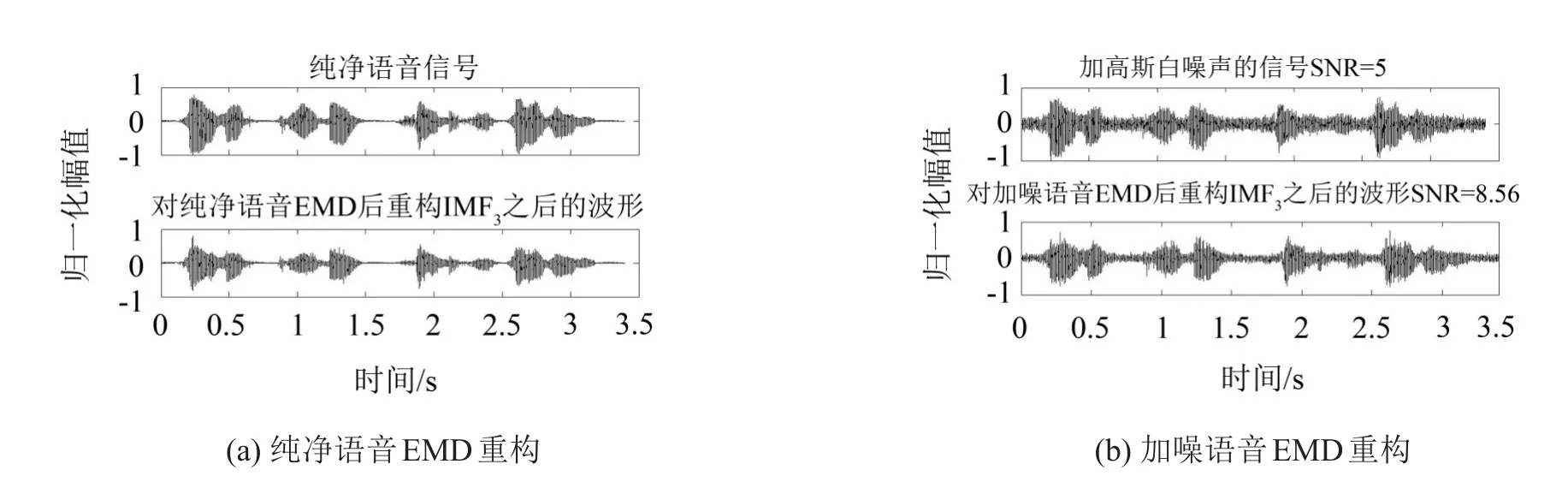
图2 EMD分解后重构

离散小波变换可以被表示成由低通滤波器和高通滤波器组成的“一棵树”，语音信号通过这样的一对滤波器进行分解称为一级分解，在信号分解过程中可以迭代进行多级分解[14]。利用小波变换进行基音周期检测时，基音周期检测前已经通过EMD分解滤波和去除低频信号，而基音的频率范围绝大部分都在60 Hz～450 Hz，本文另辟蹊径尝试EMD分解后得到模式分量imf3－imf6，采集语音信号后将imf1和imf2高频部分直接丢弃，得到中频和低频信号，但是计算机交流隔离并不理想，经常会产生50 Hz工频噪声干扰，所以本算法尝试丢弃imfi之后的分量，实验分析丢弃imf7及之后分量实验效果最佳。如此操作就相当于给语音信号设置了一个截止频率较低的带通滤波器，因此只需要进行一次小波变换便可检测出语音信号的基音周期[15]。

2.2 短时自相关函数法

语音信号时间序列为x(n)，经过EMDDWT处理后的第i帧语音信号为x′i(n)，帧长为N，则x′i(n)的短时自相关函数为

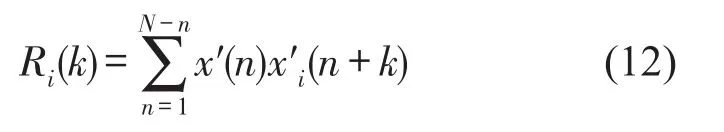
式(12)中的k是时间延迟量。

自相关函数（ACF）有一些很特别的性质，其自相关函数Ri(k)与原始信号x′i(n)的周期P是相同的，Ri(k)的峰值特性也是随着x′i(n)周期P变化在基音频率整数倍时达到，且Ri(k)是偶函数，有Ri(k)=-Ri(k)。

本文结合改进的EMDDWT与自相关函数计算得到基音周期估计值，图3给出一帧带噪清音信号和基于自相关函数、小波-自相关函数以及本文方法的一帧带噪浊音的基音周期检测结果。由图3(b)可知，一帧带噪清音在原始自相关函数下会含有大量谐波和噪声波，而图3(c)表明小波-自相关函数可以一定程度消弱谐波和噪声波的影响，但效果不明显。在图3(d)中可以看出本文改进的EMD小波算法加权短时自相关法可以有效消除原始信号帧中的谐波与噪声干扰，很好保留基波的特性。

图4给出的是一帧带噪浊音信号和基于自相关函数、小波-自相关函数以及本文方法的一帧带噪浊音的基音周期检测结果。由图4(b)可知，一帧带噪浊音在原始自相关函数下会含有较高的第1共振峰的干扰，而共振峰是产生倍频错误的重要因素，所以消弱第1共振峰干扰有利于基音周期检测准确性，图4(c)表明小波-自相关函数已经消弱60%左右第1共振峰干扰，但是，算法运用在实际基音周期检测中不太理想。从图4(d)可以看出本文算法可以减弱90%左右第1共振峰干扰，故检测基音周期效果优越。因此，本文EMDDWT-AFC算法还是有效且实际可行的。

3 算法流程

设带噪信号为x(t)，本文检测基音周期算法的步骤如下：

步骤2：在初步预处理后进行EMD分解，提取imf3及之后的分量进行重构；

步骤3：对EMD重构后的信号进行第1次分帧，第1次分帧是要进行能熵比端点检测和元音主体检测；

步骤4：在步骤2中对信号重构后，对新信号再进行EMD分解，并提取新分解imf1－imf6进行第2次重构，然后对重构信号第2次分帧，为基音周期检测做准备；

步骤5：对步骤3检测到的元音主体部分对应步骤4中的每一加噪语音帧信号先做小波变换，对变换后的数据，用小波低频系数重构，然后再计算归一化自相关函数；

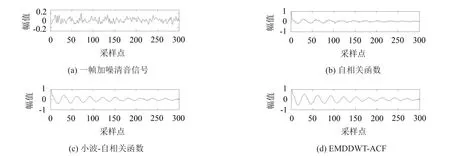
图3 一帧带噪清音与几种函数提取的相关函数值对比图

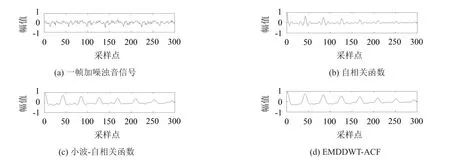
图4 一帧带噪浊音段与几种函数提取的相关函数值对比图

步骤6：对上面步骤的结果进行峰值检测，得到基音周期及其频率。

4 实验结果及分析

实验所用的语音为在实验室安静环境下用专业录音设备录制的一段语音，为“妈妈、好吗、上马、骂人”的一段包含汉语4个声调的纯净语音信号，信号样本为单声道，采样频率为8 kHz，精度为16 bit的量化.wav文件。实验中加入的噪声是来自NOISEX-92数据库中的高斯白噪声，设置信噪比（SNR）为5 dB，纯净语音与带噪语音波形如图5所示。

对加入噪声的信号进行EMD分解，提取IMF3及之后的分量，进行重构，设语音分帧的帧长为200 ms，帧移为80 ms，图6表示为语音的EMD分解第1次重构与第1次分帧后信号能熵比端点检测。

将第1次重构后的信号进行EMD 2次分解提取imf1～imf6之间的分量进行2次重构，用重构后的信号进行滤波，再结合元音主体检测到的语音段进行基音周期检测（这里的算法只是针对检测到的语音段进行基音检测，而没有检测到的部分自动忽略，故图7中的基音周期有部分无信号是正常情况），分别用自相关法、小波-自相关法及本文方法进行基音周期检测的对比实验，结果如图7所示。

图7为5 dB White Gaussian噪声工况下使用椭圆带通滤波器且在相同端点检测算法情况下基于传统自相关法、小波-自相关法和本文EMDDWT-ACF方法的基音周期检测结果。图7中的横坐标为时间刻度帧数，基音周期的纵坐标为采样点数，基音频率则表现为语谱图上的基频频率。

图7(a)表示基于传统自相关法的基音周期检测结果，从基音周期上看，尽管有椭圆滤波器的优化，但是依然会出现大量基音周期倍频和半频错误，从语谱图上可以看出检测得到的基音频率和实际的基音频率还是有出处，特别在“好吗、上马”这一段检测到的基音频率明显有偏差。

图7(b)则表示小波-自相关法基音周期检测结果，与传统自相关方法相比较，其基音周期的倍频和半频有些减少，但并不能从根本上改善其定位偏差的问题，在“上马”这段语音的语谱图上可以看出小波-自相关法依然出现错误检测。

图5 原始语音与加噪语音的波形图

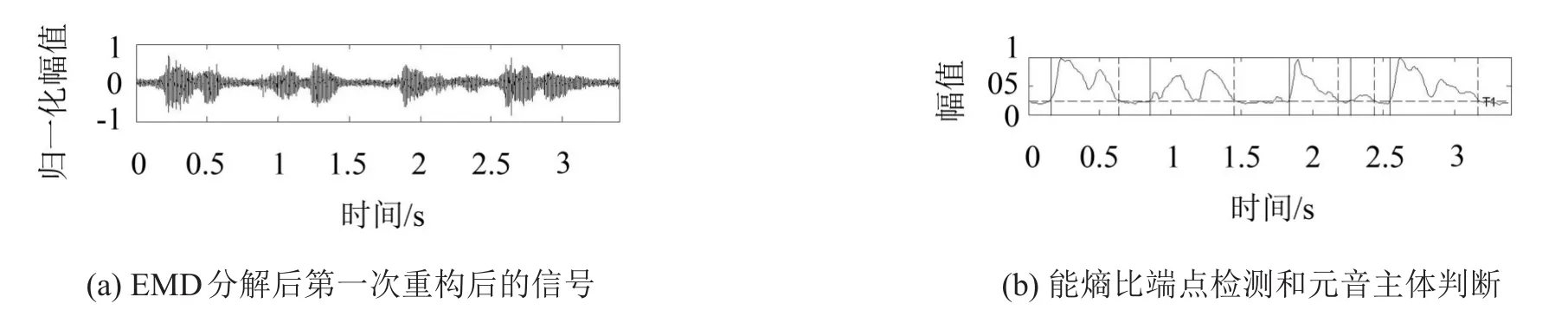
图6 元音主体检测

图7 基音检测结果对比图

而采用本文提出的EMDDWT-ACF方法时，信号经过EMD分解与重构后一系列增强、滤波过程，从图7(c)中可以看出基音周期检测中出现的倍频、半频错误以及错误检测等都得到极大减少，从语谱图可以看出，由该算法得到的基音频率与实际基频的吻合程度（准确率）高。

为了验证本文方法的实际检测准确率和稳定性，选择50个以中国大小城市的名字及部分城市飞机场的纯净原声（25个男声、25个女声），在原始语音中分别加入信噪比为5 dB、0 dB、-5 dB的高斯白噪声、粉色噪声以及人声，对纯净语音采用平均幅度差自相关函数法结合人工矫正得到的基音周期作为参考标准，允许参考误差为±8%，对基于文中提出的算法与自相关函数法、小波-自相关法的基音周期检测正确率进行比较。表1说明本文方法有更好的检测性能和抗噪能力，即使在低信噪比白噪声的情况下，准确率都是在80%以上，而小波-自相关方法在75%左右，提高了5个百分点，而自相关方法则更低。从而验证本文方法的准确率和稳定性。

从表1中的pink噪声和babble实验数据可以看出即使在不同噪声下，本文算法适应性都较为良好。在表1中的-5分贝babble噪声下，传统自相关法已经失效，而本文算法依然有75%左右的准确率。

但是本算法出发点在于EMD，而更加复杂环境下的噪声其频率范围各有不同且比较广泛。当纯净语音与这些噪声混合，本算法利用分解后的imf3～imf6重构就不是很适用，因为噪声频率范围广，所以提取imf3～imf6就有一定局限性。本文算法的不足之处在于当被检测的语音处于复杂噪声环境下的时候，算法的适应性较差，而这正是接下来要研究的课题。

5 结语

本文以含噪语音的基音周期检测为研究对象，提出了一种基于EMD改进的小波-自相关的基音周期检测算法。根据MATLAB软件仿真实验结果可知，这种新的基音周期检测算法有更高的检测精度和很好的基音周期检测实用性，当然本算法只是部份解决了基音周期检测的问题，而想要在更加复杂的环境下寻找更完美的基音周期检测算法的道路还很漫长。

表1 基音周期检测准确率对比

参考文献：

[1]J S JUNG,J J KIM,M J BAE.Pitch alteration technique in speech synthesis system[J].IEEE Transactions on Consumer Electronics,2001,47(1):163-167.

[2]DAVID A,KRUBSACK,RUSSELLl J,et al.An autocorrelation pitch detector and voicing decision with confidence measures developed for noise-corrupted speech[J].IEEE Transactions on Consumer Electronics,1991,39(2):319-328.

[3]ROSS M,SHAFFER H,FREUDBERG R,et al.Average magnitude difference function pitch extractor[J].IEEE Transactions on Acoustics, Speech and Signal Processing,1974,22(5):353-362.

[4]NOLL A M.Cepstrum pitch determination[J].Journal of theAcoustical Society ofAmerica,1967,41(2):293-309.

[5]陈磊，吴小培，吕钊.基于线性预测与归一化互相关的基音周期检测[J].电子测量技术，2009，32(10)：20-23.

[6]AMIN S L,JALIL S.Pitch detection of speech signal using wavelet transform[J].International Journal of Scientific Engineering and Technology,2015,5(4):322-324.

[7]杨龙.基于小波变换的自相关基音周期检测方法[J].信息通信，2015，1(9)：72-73.

[8]陈小利，徐金甫.利用小波变换加权自相关的基音周期检测法[J].数据采集与处理，2007，22(4)：463-467.

[9]潘峥嵘，戴芮，张宁.改进的基音周期检测算法研究[J].计算机工程与应用，2015，51(10)：223-226.

[10]宋之用.MATLAB在语音信号分析与合成中的应用[M].北京：北京航天航空大学出版社，2013：251-258.

[11]宗源，李平，曾毓敏，等.基于EMD的ACF基音周期检测改进算法[J].南京师大学报(自然科学版)，2013，36(3)：42-47.

[12]王建军，侯盼卫，苏新彦，等.EMD去噪法在FMCW雷达信号处理中的应用[J].科学技术与工程，2014，14(27)：66-70.

[13]李曼曼，杨鸿武，洪宁，等.基于EMD的带噪语音端点检测[C].第十一届全国人机语音通讯学术会议，西安，2011：60-64.

[14]张雪英.数字语音处理及MATLAB仿真[M].北京：电子工业出版社，2010：220-224.

[15]李辉，戴李辉，戴蓓蒨，等.基于前置滤波和小波变换的带噪语音基音周期检测方法[J].数据采集与处理，2005，20(1)：100-104.