车端风挡类型对高速列车气动噪声影响规律的研究

刘国庆，杜 健，刘加利，崔振山

（1.上海交通大学 材料科学与工程学院塑性成形技术与装备研究院，上海 200030；2.中车青岛四方机车车辆股份有限公司，山东 青岛 266111）

研究表明，当高速列车时速超过300公里后其气动噪声迅速增大，气动噪声成为列车的最主要噪声[1]。气动噪声不仅会影响车内乘员的舒适度，还会对车外周围生活环境造成严重干扰[2]。随着保护环境的相关法律法规对噪声要求越来越严，气动噪声问题已经成为限制列车速度的主要因素[3]。高速列车行驶时，当气流沿车体表面向后流经车厢连接处时，由于缝隙的存在，产生复杂的旋涡流动，导致车体表面动压增大，噪声随之增大，车端风挡成为列车气动噪声的主要来源之一。所以，研究车端风挡的连接类型对高速列车气动噪声的影响，对高速列车减阻降噪设计具有重要意义。

目前，国内外很多学者都在致力于通过试验和数值模拟，开展高速列车车端风挡气动噪声的研究工作。Yamazaki等通过对1:5缩比的某型新干线列车的风洞试验和实车测试，发现车端是高速列车的主要噪声源[4]。黄莎等采用大涡模拟与声类比理论，研究了高速列车车端风挡长度和深度对列车气动噪声的影响[5]。杨加寿等研究和对比了7种不同风挡类型对高速列车阻力和升力的影响[6]。不过，当前高速列车车端风挡类型对气动噪声的影响规律的研究仍然相对较少，主要原因之一就是由于车端风挡尺寸相对整体车体比较小，需要采用较大的风洞模型进行试验才能测得车端风挡的气动噪声。

本文基于1:8缩比的三节车体组成的某型高速列车简化模型，在时速350公里的工况下，对车端风挡采用某型既有半包风挡和既有全包风挡两种情况进行数值模拟研究，分析两种风挡类型对列车周围气动噪声的影响，并对其气动噪声的差异进行对比分析，从而为选择风挡类型提供依据。

1 车端风挡噪声计算方法

目前，工程中气动噪声仿真计算的最佳方案是将计算分为近场分析计算和远场分析计算两部分，该方法具有很大的适用性。在本文的近场分析计算中采用大涡模拟（LES）方法获得非定场流场分布，远场气动噪声计算时采用Lighthill声学比拟理论提取噪声源。

1.1 基于大涡模拟的近场分析计算方法

大涡模拟(LES)是近年来在计算流体力学领域新发展起来的一种重要的数值计算方法，其通过滤波函数把湍流运动分为大尺度涡和小尺度涡，大尺度涡采用直接数值模拟计算，对于小尺度涡，建立亚格子尺度模型来封闭，滤波后的流体连续性方程和动量方程[7-9]分别为

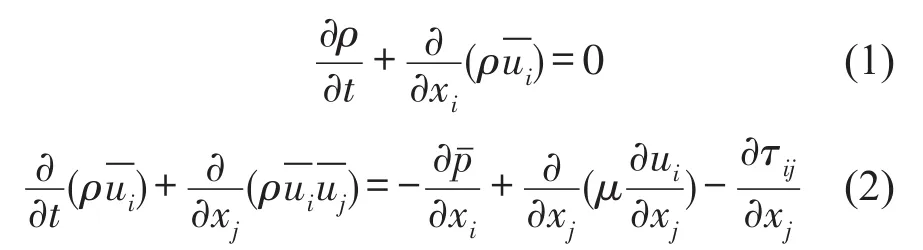
其中：ρ是流体密度；μ是湍流黏性系数；τij是亚格子尺度应力，它度量了小尺度涡的运动对大尺度涡运动的影响，本文采用Smagorinsky-Lilly亚格子模型[10]，其方程为

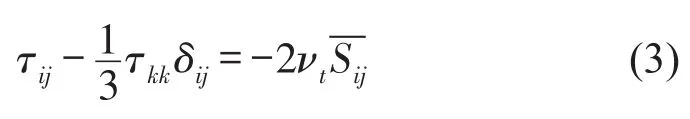
δij为克罗内克函数，νt是亚格子尺度涡黏系数。式（1）、式（2）、式（3）组成封闭方程组。

1.2 基于Lighthill声学比拟理论的远场气动噪声计算方法

利用质量守恒方程和动量方程，Lighthill推导出声传播方程为[11]

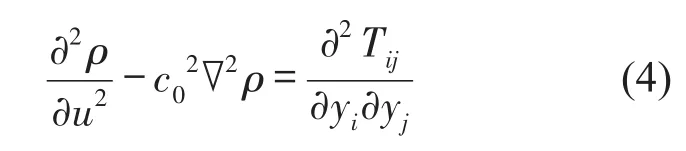
式中：ρ是流体密度；Tij为Lighthill应力张量

式中：p是静压力；c0为声速；eij为黏性应力张量，当雷诺数比较小时，可以考虑不计。

Ffowcs Williams和Hawkings应用广义函数法进行了更深一步的拓展，建立了著名的福茨.威廉姆-霍金斯方程（FW-H方程）[12]，该方程可以解决运动物体在流体中发声的问题，具体为

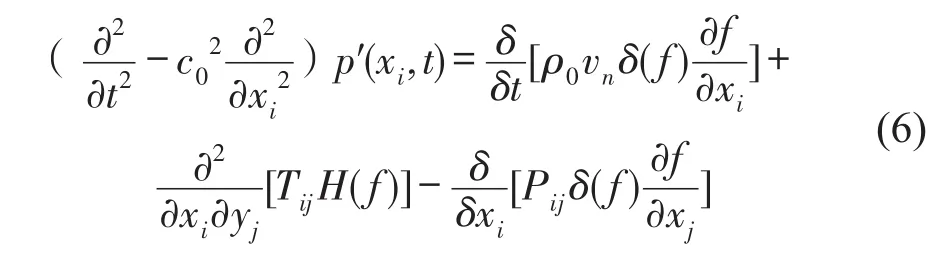
式中：f是包括运动物体的控制方程；H(f)是Heaviside函数；Pij为物体表面应力张量；vn为物体表面法向速度；p′(xi,t)是t时刻在噪声监测点处的声压值；δ(f)是Dirac函数。第三项是偶极子声源项，由物体表面脉动压力引起。对于时速低于400 km/h的高速列车，可以仅考虑偶极子声源项。因此，高速列车的偶极子声源项的分布特征和大小决定了外场气动噪声分布规律和大小。

先通过大涡模拟（LES）和亚格子尺度模型计算物体表面脉动压力，从而获得噪声流场中的偶极子声源项，然后将流场的时域信号转换为频域信号，最后计算远场的气动噪声。

1.3 不同风挡样式的计算模型

某型高速列车既有半包风挡和既有全包风挡的模型如图1所示。

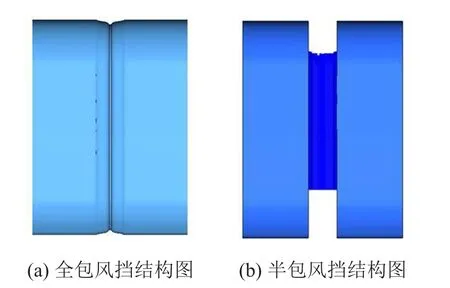
图1 某型高速列车两种典型风挡类型

半包风挡的两侧采用全包风挡结构，上下采用开口风挡，其中风挡高度为2.4 m，宽度分别为0.46 m和0.38 m；全包风挡两侧高3.64 m。全包风挡在车端处采用曲面光滑过度。

1.4 模型的计算域、网格划分及边界条件设置

采用1:8的3车编组计算模型，其车身长l=9.98 m，车高度h=0.507 m，宽度w=0.42 m。根据计算要求和有关参考文献，取计算域长度为50 m，宽度为14 m，高度为10 m。计算域尺寸和坐标的定义见图2。

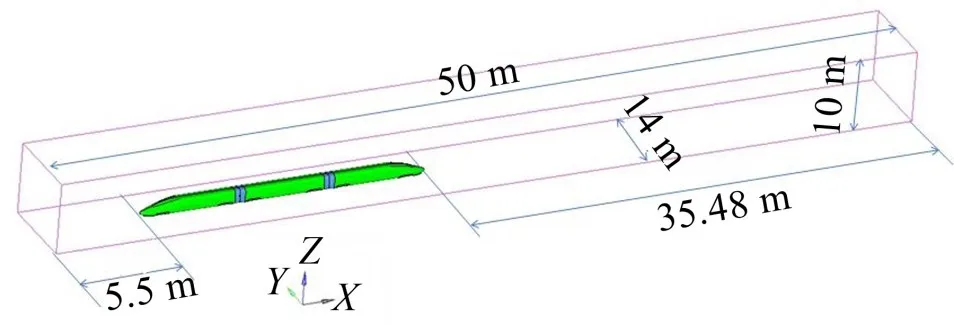
图2 3节编组高速列车的1:8计算域

在LES的计算中，采用靠近车体表面用非结构四面体网格、远离车体用6面体网格的混合网格生成方法。为了能准确地模拟出列车车体周围流场的细节，在车体近壁面生成10层边界层，总厚度为4 mm，第1层单元厚度尺寸为0.1 mm；在列车表面由内向外建立3个加密区，使网格密度逐渐由密向疏过渡，总单元数约为4 600万。

列车车体表面设置为无滑移边界条件；地面设置滑移壁面条件，滑移速度与列车速度相等；流动进口定义为速度进口边界，大小等于列车运行速度350 km/h；流动出口定义为压力出口边界；为了降低边界的影响，剩余边界均设置为对称边界。

1.5 车端风挡气动噪声监测点布置

为了研究车端风挡的气动噪声，按照噪声测量标准ISO3095-2005，结合本模型是1:8缩小模型的特点，沿列车X方向，在离轨道高0.437 5 m、车体中心线3 m处，从列车鼻尖开始每0.125 m布置一个噪声监测点，共计80个点；沿列车Y方向，在靠近车头位置的一位端风挡和远离车头位置的二位端风挡中心处，在离轨道高0.437 5 m、离车体中心线0.937 5 m、1.5 m、2.312 5 m、3.75 m处分别布置4个噪声监测点，共计布置8个噪声监测点；沿列车Z方向，在一位端风挡、二位端风挡中心处，在离轨道高0.062 5 m、0.15 m、0.275 m和0.625 m、离车体中心线1.5 m处，分别布置4个噪声评估点，在Z向共计布置8个噪声监测点，噪声监测点布置如图3所示。

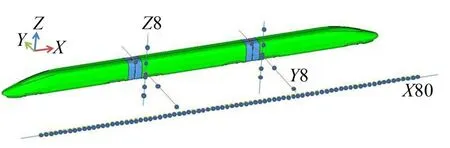
图3 车端气动噪声监测点布置示意图

2 数值计算结果分析

2.1 不同风挡类型工况下远场气动噪声数值分析结果

将车端1位端风挡和2位端风挡作为声源，通过对各监测点的声压级频谱进行分析对比发现，安装两种风挡的高速列车在对应的监测点位置，其监测点气动噪声频谱相似，仅声压级不同。图4是采用全包风挡和半包风挡模型在监测点X15处频谱对比图，该点位于1位端风挡的中心位置。从图4(a)中可以看出，车端风挡气动噪声的频率分布广，在2 500 Hz范围内都存在声压，因此是一宽频噪声，并且监测点声压级随频率变化而改变；采用全包风挡模型比采用半包风挡模型，声压级平均减低6.9 dB。由图4(b)可见，车端风挡气动噪声能量主要集中在80 Hz～930 Hz范围内。

由图5(a)可见，当高速列车以时速350公里运行时，气流通过全包风挡时，由于在车端间隙采用了流线型的曲面过渡，气体在此处滞留小，进而引起的气动噪声较小。而从图5(b)可看出，当车顶气流穿过半包风挡结构时，由于车端处间隙的存在，气体进入间隙内形成漩涡，引起较大的速度变化，因此半包风挡处气动噪声较大。

图4 全包风挡和半包风挡模型在监测点X15处频谱图对比

图5 车端采用全包风挡和半包风挡时纵向对称面上的速度流线对比图

图6是以风挡为噪声源，采用不同风挡得到的列车运行方向（X向）声压级对比曲线。由图可见，对于两种风挡结构，1位端风挡引起噪声的声压级总比2位端风挡大，噪声在风挡位置处达到局部最大；采用全包风挡结构比采用半包风挡结构可使最大声压级下降3.1 dB(A)。

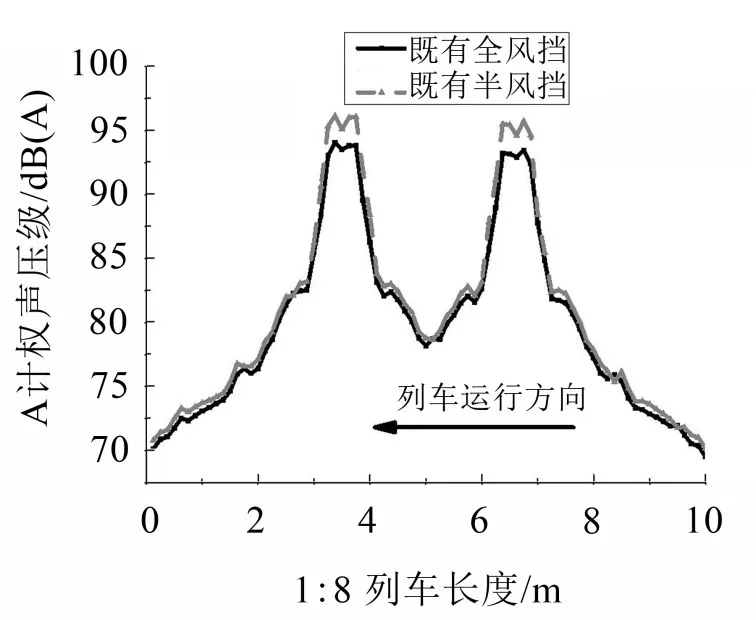
图6 车辆连接处不同风挡工况下X向声压级对比曲线

图7为Z=0.437 5 m的两种风挡工况下沿Y向不同噪声监控点声压级的对比图。

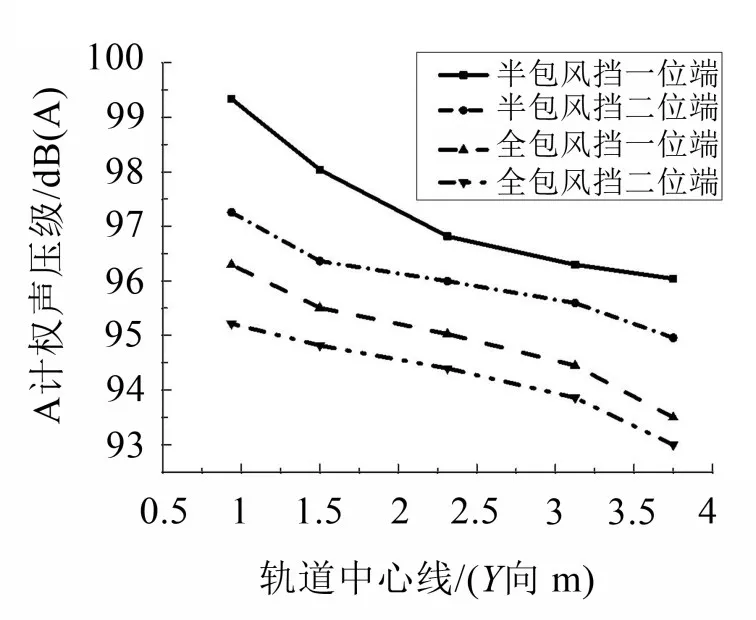
图7 车辆连接处不同风挡工况下Y向声压级对比曲线

由图可见，对于每一种风挡，一位端风挡引起噪声的声压级总比二位端风挡大；Y向声压级衰竭幅度不同，采用半包风挡，一位端风挡的衰竭幅度为3.1 dB(A)，二位端风挡为2.2 dB(A)，采用全包风挡时，一位端风挡衰竭幅度为2.0 dB(A)，二位端风挡为1.37 dB(A)，因此采用半包风挡时一位端风挡沿Y向声压级衰竭幅度最大；随着距轨道中心线距离的增加，声压级都逐渐降低，在相同的噪声监控点，半包风挡的声压级总大于全包风挡的声压级，在距车体中心线0.937 5 m的监控点Y1处，二者声压级差为最大，最大差值为3.04 dB(A)。

图8为车端采用不同风挡时，Z向等效连续A计权声压级曲线对比图。

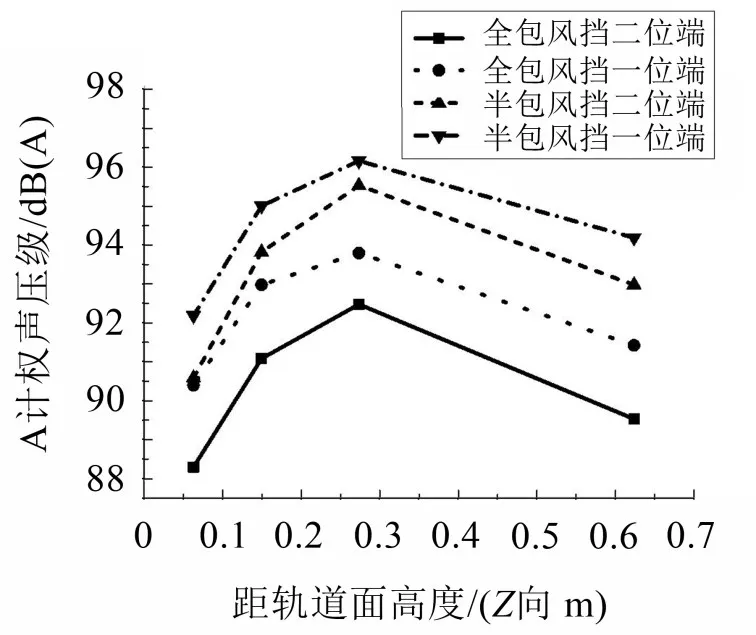
图8 车端不同风挡工况下Z向声压级对比曲线

可见，风挡的气动噪声沿Z向差别较大，并且在距离轨道高度0.275 m时，气动噪声达到最大，半风挡时1位端的声压级为96.2 dB(A)，全风挡时1位端声压级达到93.8 dB(A)，因此采用全风挡方案，声压级最大降幅可达2.4 dB(A)。

3 结语

通过对某型高速列车典型的半包风挡、全包风挡工况下气动噪声进行数值模拟计算分析和对比，可以看出：

(1)车端风挡气动噪声是宽频噪声，声压级随频率变化，气动噪声能量主要集中在80 Hz～930 Hz。

(2)无论采用何种风挡结构，在列车X向和Y向一位端风挡引起的噪声都比2位端风挡大。

(3)全包风挡方案减小了气流扰流，与半包风挡方案相比，X向声压级最大降幅达3.1 dB(A)，Y向声压级最大降幅达3.04 dB(A)，Z向声压级最大降幅达2.4 dB(A)，降噪明显。

参考文献：

[1]杜健，梁建英，田爱琴.高速列车受电弓气动噪声特性分析[J].西南交通大学学报，2015，50(5)：935-941.

[2]杨国伟，魏宇杰，赵桂林，等.高速列车的关键力学问题[J]. 力学进展，2015，45：217-460.

[3]HE BIN,XIAO XINBIAO,ZHOU QIANG,et al.Investigation into external noise of a high-speed train at different speeds[J].Zhejiang University-Sci A(Apply Phys&Eng)2014,15(12):1019-1033.

[4]YAMAZAKIN,TAKASHIT.Wind tunnel test on reduction of aeroacoustic noise from car gaps and bogie sections[J].QR of RTRI,2007,48(4):229-235.

[5]黄莎，梁习峰，杨明智.高速列车车厢连接部位气动噪声数值模拟及降噪研究[J].空气动力学学报，2012，30（30)：254-259.

[6]杨加寿，蒋崇文.车厢间风挡形式对高速列车气动性能的影响[J]. 铁道学报，2012，34（11）：29-35.

[7]FELTEN F.FAUTRELLE Y.DU TERRALL Y,et al.Numerical modeling of electrognetically-riven turbulent flows using LES methods[J].Applied Mathematical Modeling,2004,28(1):15-27.

[8]MARTÍNEZ-LERA P,SCHRAMB C,BERIOT H.An approach to aerodynamic sound prediction based on incompressible-flow pressure[J].Journal of Sound and Vibration,2014,333(1):132-143.

[9]刘加利，张继业，张卫华.高速列车车头的气动噪声数值分析[J].铁道学报，2011，33（9）：19-26.

[10]俞建阳，王若玉.不同亚格子模型的对比分析及其运用[J].工程热物理学报，2016，37（11）：2311-2318.

[11]LI HENG,HAO ZHIYONG,ZHENG XU,et al.LESFEM coupled analysis and experimental research on aerodynamic noise of the vehicle intake system[J].AppliedAcoustics,2017,116(15):107-116.

[12]GLEGG STEWART,DEVENPORT WILLIAM.Aeroacoustics of low mach number flows[M].Academic Press,2017:95-114.