基于蒙特卡罗模拟的混凝土坝渗流性态区间综合评价

李家田,苏怀智,赵海超,王少波

(1. 河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098; 2. 河海大学水利水电学院,江苏 南京 210098;3. 江苏省水利勘测设计研究院有限公司,江苏 扬州 225127)

混凝土坝的渗流性态评价是大坝安全评估过程中的重要环节[1]。由于坝体及基础裂隙结构复杂,渗流过程往往涉及诸多要素,因此混凝土坝的渗流性态综合评价是一项复杂的系统工程。近年来,不少学者针对大坝渗流性态评价开展了较多工作:梅一韬等[2]基于熵权法与物元可拓理论实现了对混凝土坝渗流性态的模糊综合评价;苏怀智等[3]将集对分析理论引入渗流性态评价中,并综合考虑了渗流发展趋势,使评价内容更加全面;郭娜等[4-5]从数值模拟的角度,通过建立渗流模型,采用有限元法对大坝渗流性态进行了评估。然而,影响渗流性态的因素众多且复杂,目前的成果依然存在主观性较大的问题。在渗流性态评价过程中,专家针对评价项目的打分环节是决定最终评价结果的关键,同时也是影响评价结果主观性的主要来源[6]。目前的渗流性态评价方法在专家打分阶段普遍采用单值赋分的形式,涵盖信息量较少,主观性过强,不能充分体现专家意见,与实际情况不符。

为了减少主观随意性的影响,提高评价结果的精度,本文采用专家区间打分的形式,综合考虑各个专家意见,并利用蒙特卡罗模拟方法实现对混凝土坝渗流性态的综合评价。

1 混凝土坝渗流性态综合评价指标体系

由于混凝土坝坝体设有分缝,其渗流性态的评估往往分坝段独立进行。对于各坝段而言,根据相关文献与规范[7-9],其渗流性态指标体系分为3个层次:第1层为评估的目标层,即坝段渗流性态;第2层为评估的准则层,即各监测项目,包括扬压力、绕坝渗流与渗漏量;第3层为影响因素层,即监测项目对应的测点数据。由此构建的渗流性态综合评价指标体系如图1所示。

图1 混凝土坝渗流性态综合评价指标体系

2 基于蒙特卡罗模拟的区间综合评价

2.1 蒙特卡罗法

蒙特卡罗法是一种有效的随机模拟方法[10-11],通过建立某一事件的概率统计模型,借助计算机程序,对该事件进行大量抽样计算,并对结果进行统计分析。根据大数定律及中心极限定理,当抽样的次数足够大时,模拟的结果是真实可信的[12-13],因此蒙特卡罗算法经常被应用于可靠度计算以及风险评估领域[14-15]。

在混凝土坝渗流评价过程中,由于专家数量有限,往往一位专家的打分出现偏差就会对评价结果的准确度产生较大影响,故本文采用蒙特卡罗法,在已知评分区间以及分值概率分布的条件下,通过模拟大量专家评分过程,消除个别专家主观性所引起的评价结果误差。

2.2 评分区间的确定方法

在专家打分环节,对于某一监测项目,可组织多名专家独立地进行区间评分,各自给出该监测项目所得分值的上下限。假定共有s名专家参与评审,且第t名专家所给的评分区间为[at,bt](t=1,2,…,s)。为了获取该监测项目的最终得分区间[a,b],需要对各组专家的打分区间进行数学处理。考虑到参评专家的评价水平可能存在差异,譬如院士及工程界权威的评分理应得到更多的重视,而传统的算术平均值法不能解决这一问题[16],故引入专家权重因子u,采用加权平均值法计算最终得分区间[a,b]。区间上下限的计算公式如下:

(1)

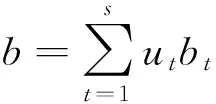
(2)

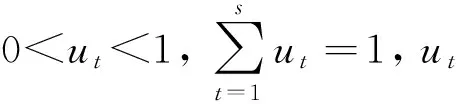
2.3 评分区间概率分布

计算区间概率分布函数是进行蒙特卡罗模拟的前提,传统的计算方法往往依赖于大量样本数据,通过对样本数据进行拟合确定其概率分布函数[17]。然而在工程安全评价领域,参与评分的专家数量有限,难以获得大量评分样本,因此,传统的概率分布计算方法并不适用于渗流性态评价。

从区间概率分布函数的现实含义看,分值在区间的概率分布实际上反映了专家意见的分布情况,由于各个监测项目的评分区间是由多位专家共同决定的,考虑到专家之间可能出现意见分歧,因此,本文利用区间概率分布函数来刻画专家在打分过程中的意见分歧程度。

一般情况下,对于某一监测项目而言,若专家打分意见一致,分值集中,则所获得的评分区间较窄,且分值在评分区间的概率分布呈单峰状,如图2(a)所示,表明该项目所得分值出现在区间中心的概率较大,出现在区间边缘的概率较小;若专家打分意见分歧严重,分值分散,则所获得的评分区间较宽,且分值在评分区间的概率分布呈多峰状,如图2(b)所示,表明该项目所得分值出现在区间各处的概率基本均等。对于某一监测项目,假设专家给定的的评分区间为[a,b],区间宽度C=b-a,定义Q为专家意见分歧程度判别值。在此基础上,利用以下准则计算该监测项目在专家评分区间的概率分布:

a. 当C≤Q时,认为专家意见较为一致,评分值的概率分布在该区间上呈单峰状,为简便起见,采用在区间[a,b]上的双侧截尾正态分布函数作为评分值在该区间的概率分布。根据正态分布的“3En规则”[18-19],利用式(3)及式(4)确定原正态分布函数的数学期望E0及标准差σ0,进而对原正态分布函数在区间[a,b]上进行数学变换得到对应的截尾正态分布函数,同时确定其数学期望E及标准差σ。

(3)

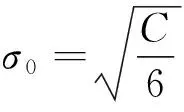
(4)

b. 当C>Q时,认为专家意见分歧较大,评分值的概率分布在该区间上呈多峰状。为简便起见,以均匀分布函数作为评分值在该区间的概率分布,其数学期望E及标准差σ为

(5)

(6)

图2 评分区间概率分布类型

2.4 主观权重修正

利用层次分析法(AHP法)可以便捷地对各评价指标赋权,其实质是由决策者基于经验主观确定[20],因此,一般需要计算客观权重以修正主观权重。客观权重的计算一般基于熵权法,标准差法等,其基本思想是一致的:信息离散程度越高,认为其信息价值越大,相应的权重也越大。考虑到蒙特卡罗模拟过程中需要进行大量的迭代计算,传统的主观权重修正法费时费力,为此提出一种较为简明的基于评分区间宽度的主观权重修正方法。

对于某渗流性态评价指标而言,专家给出的打分区间宽度越大,一定程度上表明该指标得分离散程度越高,其权重理应越大。据此定义渗流性态评价指标的主观权重修正公式如下:

(7)

对所有修正后的主观权重进行归一化处理即得到本文所需的各评价指标权重值。

3 渗流性态区间综合评价实现过程

3.1 综合评价指标与分级

根据已构建的混凝土坝渗流性态综合评价指标体系,以扬压力、绕坝渗流与渗漏量为评价指标,依据常用分级标准[2],将渗流性态划分为“正常”“基本正常”“轻度异常”“异常”“险情”5个评价等级,具体的分级标准如表1所示。

表1 混凝土坝渗流性态综合评价指标分级

3.2 基于蒙特卡罗模拟的区间评价步骤

步骤1组织专家分析渗流监测数据,分别对3项评价指标进行区间打分,同时利用层次分析法计算各指标的主观权重;

步骤2计算各指标评分区间宽度,利用评分区间的概率分布计算准则及式(3)至式(6)确定区间概率分布函数,同时利用式(7)修正主观权重值,经归一化处理得到指标权重向量;

步骤3采用MATLAB软件进行蒙特卡罗模拟,产生符合区间分布的评分向量,计算其加权得分,模拟N次直至结果收敛,统计结果并进行渗流性态分析评价。

评价流程如图3所示。

图3 混凝土坝渗流性态综合评价流程

4 实例分析

某混凝土重力坝最大坝高152.0 m,坝顶长404.5 m,坝顶高程198.0 m,正常蓄水位191.0 m。为查明该混凝土坝目前的渗流状况以开展除险加固工作,需对各坝段扬压力、渗漏量及绕坝渗流等监测资料进行分析处理。本文以7号典型坝段为例,依据温度、降水等相关环境量,选取渗流较为显著的时段(2016年9月)的监测数据进行渗流性态评价。

4.1 基础数据

组织专家分析监测资料,结合现场考察情况对渗流评价指标进行打分,并基于层次分析法进行主观赋权,评分及主观权重见表2。

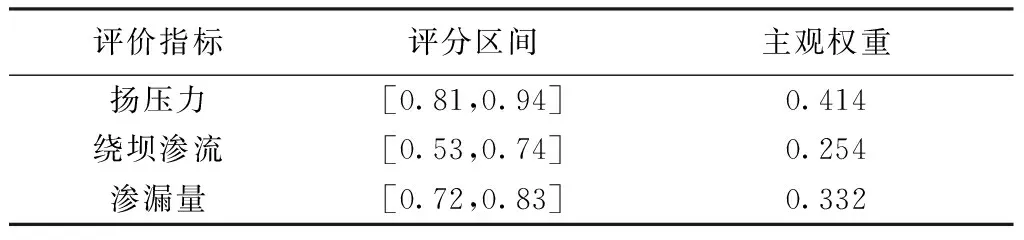
表2 评分及主观权重

4.2 区间处理与权重修正

分别计算各评价指标得分区间宽度C1、C2、C3,基于得分区间的概率分布计算准则,考虑到表1中各评价指标均以0.2为区间宽度界限进行分级,故取专家意见分歧程度判别值Q为0.2,由此确定各指标评分区间概率分布类型及参数;利用式(7)对表2的主观权重值进行修正,并做归一化处理,所得结果如表3所示。

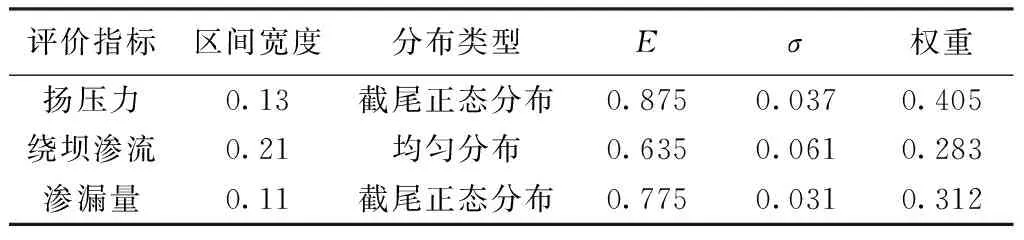
表3 评分概率分布及指标权重

4.3 模拟计算

分别取模拟次数N为1 000、10 000、100 000,利用MATLAB软件进行蒙特卡罗模拟计算,当N达到100 000时,结果已经收敛,此时渗流性态评价结果统计情况见表4。

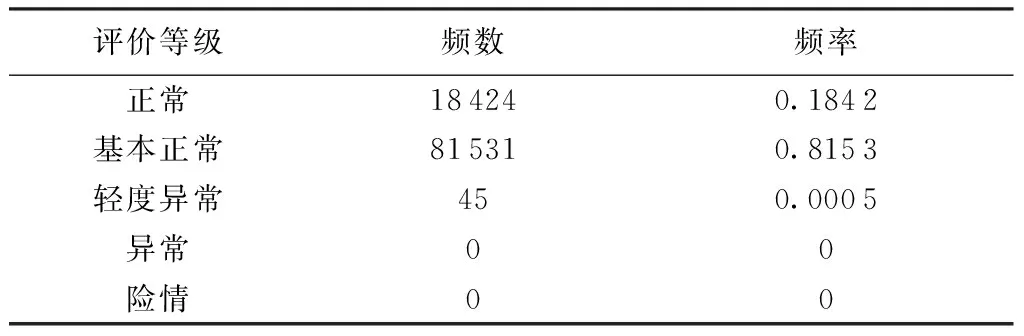
表4 评价结果统计

4.4 结果分析

考虑到模拟次数足够大,故可以将各评价等级的统计频率作为本次渗流性态评价结果的概率。由表4可知,该混凝土坝7号坝段渗流性态综合评价等级为正常的概率为18.4%,基本正常的概率为81.5%,换言之,该坝段渗流性态评级在基本正常及以上的概率高达99.9%,暂时不需要进行防渗方面的除险加固工作,从最大概率的角度考虑,可将该坝段渗流性态评价等级定为基本正常,这与某委托机构基于传统单值打分法得出的结论一致。由此可见,在评价指标不确定性较高的情况下,基于蒙特卡罗模拟的区间评价法具有可操作性好、容错率高的优势。

5 结 语

将蒙特卡罗模拟法引入混凝土坝渗流性态评价中,在专家打分阶段采用区间打分的形式,综合考虑了专家评审水平间的差异,并利用区间概率分布函数反映专家意见分歧情况,涵盖信息丰富,较好地解决了传统单值赋分导致评价结果主观随意性过强的问题。出于实用性的考虑,本文使用简明的截尾正态分布与均匀分布函数表征专家意见分歧状况,这与真实情况有一定的差距,后续可考虑采用更加复杂的分布函数以提高评价精度。此外,专家意见分歧程度判别值的客观取值也是未来研究的重点。

参考文献：

[ 1 ] 吴中如. 水工建筑物安全监控理论及其应用[M]. 北京: 高等教育出版社, 2003.

[ 2 ] 梅一韬, 仲云飞. 基于熵权的大坝渗流性态模糊可拓评价模型[J].水电能源科学, 2011, 29(8): 58-61. (MEI Yitao, ZHONG Yunfei. Fuzzy extension evaluation model of dam seepage behavior based on entropy weight[J]. International Journal Hydroelectric Energy, 2011, 29 (8): 58-61. (in Chinese))

[ 3 ] 苏怀智, 孙小冉. 混凝土坝渗流性态综合评价与趋势预估模型研究[J].人民长江, 2013, 44(22): 95-99, 110. (SU Huaizhi, SUN Xiaoran. Discussion on minority cultures protection in hydropower development[J]. Yangtze River, 2013, 44(22): 95-99, 110. (in Chinese))

[ 4 ] 郭娜. 浆砌石重力坝安全评价方法及应用[D]. 南京:河海大学, 2005.

[ 5 ] 刘博,沈振中,宗原. 芙蓉嶂水库大坝渗流与结构性态评价[J].水电能源科学,2008 (4): 67-69. (LIU Bo, SHEN Zhenzhong, ZONG Yuan. Analysis and appraisement of seepage behavior and structure property of earth-rock dam in Furongzhang Reservoir[J]. International Journal Hydroelectric Energy, 2008 (4): 67-69. (in Chinese))

[ 6 ] 伍晨, 赵艳玲, 孟炜. 基于蒙特卡罗模拟的区域农村饮用水水质指数评价[J]. 环境与健康杂志, 2014, 31(12): 1063-1066. (WU Chen, ZHAO Yanling, MENG Wei. Regional drinking water quality index assessment based on Monte Carlo simulation[J]. Environment and Health, 2014, 31(12): 1063-1066. (in Chinese))

[ 7 ] SL 601—2013混凝土坝安全监测技术规范[S]. 北京: 中国水利水电出版社, 2013.

[ 8 ] SU Huaizhi, HU Jiang, WU Zhongru. A study of safety evaluation and early-warning method for dam global behavior[J]. Structural Health Monitoring, 2012, 11(3): 269-279.

[ 9 ] SU Huaizhi, LI Jinyou, CAO Jiping,et al. Macro-comprehensive evaluation method of high rock slope stability in hydropower projects[J]. Stochastic Environmental Research and Risk Assessment, 2014, 28(2): 213-224.

[10] 李隐, 邓建, 彭泽. 基于蒙特卡罗模拟的边坡可靠度评价[J]. 采矿技术, 2010, 10(1): 39-42. (LI Yin, DENG Jian, PENG Ze. Evaluation of slope reliability based on monte carlo simulation[J].Mining Technology, 2010, 10(1): 39-42. (in Chinese))

[11] 李德亮, 石崇, 聂卫平, 等. 基于土性相关蒙特卡罗法的争岗滑坡堆积体可靠性分析[J]. 河海大学学报(自然科学版), 2011,39 (3): 317-322. (LI Deliang, SHI Chong, NIE Weiping, et al. Reliability analysis of Zhenggang landslide deposit based on Monte-Carlo method with relevant parameters of c and φ[J]. Journal of Hohai University(Natural Science Edition), 2011, 39(3): 317-322. (in Chinese))

[12] 康聪. 蒙特卡罗模拟在两类路径相关期权定价中的应用[D].济南:山东大学,2015.

[13] 陈铂, 罗麟. 蒙特卡罗法求大体积混凝土不稳定温度场的完整解[J]. 水利水电科技进展, 2009, 29(1): 31-34. (CHEN Bo, LUO Lin. The complete solution of mass concrete in unstable temperature field using the Monte Carlo method[J]. Advances in Science and Technology of Water Resources, 2009, 29(1): 31-34. (in Chinese))

[14] 王晶晶, 樊尊荣. 含水层非均质性对地下水蒙特卡罗模拟结果的影响[J]. 水资源保护,2017, 33(1): 46-51.(WANG Jingjing, FAN Zunrong. Impacts of aquifer heterogeneity on Monte Carlo simulation of groundwater[J]. Water Resources Protection, 2017, 33(1): 46-51. (in Chinese))

[15] 李孝全, 黄超, 徐晨洋, 等.基于改进PSO-LSSVM和蒙特卡洛法的电力系统可靠性评估[J]. 河海大学学报(自然科学版), 2016, 44(5): 458-464 (LI Xiaoquan, HUANG Chao, XU Chenyang, et al. Reliability evaluation of power system based on improved PSO-LSSVM and Monte Carlo simulation[J]. Journal of Hohai University(Natural Science Edition), 2016, 44(5): 458-464. (in Chinese))

[16] 林元庆. 专家群评价的校正：补偿方法及应用[J]. 科学学研究, 1998, 16(4): 69-75. (LIN Yuanqing. The method of correction and compensation to expert group evaluation[J]. Studies in Science of Science, 1998,16 (4): 69-75. (in Chinese))

[17] HUAIZHI Su, MENG Yang, ZHIPING Wen. Multi-layer multi-index comprehensive evaluation for dike safety[J]. Water Resources Management, 2015, 29(13): 4683-4699.

[18] 段在鹏, 钱新明, 夏登友. 基于蒙特卡洛模拟和主客观综合权重的化工园区配电系统模糊综合评价[J]. 安全与环境学报, 2016, 16(1): 15-19.(DUAN Zaipeng, QIAN Xinming, XIA Dengyou. Research on fuzzy comprehensive assessment for chemical industry park on fuzzy comprehensive assessment for chemical industry park power supply and distribution system based on Monte-Carlo simulation[J]. Journal of Safety and Environment, 2016, 16(1): 15-19. (in Chinese))

[19] 帅青燕, 何亚伯. 基于云模型的坝基岩体质量综合评价[J]. 东南大学学报(自然科学版), 2013, 43(增刊1): 54-58. (SHUAI Qingyan, HE Yabo. Comprehensive evaluation on rock quality of dam foundation based on cloud model[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(Sup1): 54-58. (in Chinese))

[20] 宋海洲, 王志江. 客观权重与主观权重的权衡[J]. 技术经济与管理研究, 2003 (3): 62. (SONG Haizhou, WANG Zhijiang. The balance of objective weight and subjective weight[J].Technoeconomics and Management Reserch, 2003 (3): 62. (in Chinese))