水下潜标布放系统水动力学分析

单海烽，朱克强，张大朋，孙兆浩

(1.宁波大学 海运学院，宁波 315211；2.浙江大学 建工学院，杭州 310058)

潜标作为现代海洋离岸监测的重要基础设施，能够自主实时对海洋水文、气象等要素进行全方面连续的监测，是海洋其他诸多探测手段在时空上的延伸拓展。潜标受固定锚的作用而锚定于特定的海底位置，通过系留索的释放器上浮回收，对水下环境剖面资料的获取尤为重要，自身优良的隐蔽性、稳定性是其他水下监测方法无法具有的，世界各国对潜标系统日益重视，后者也日益得到广泛的应用[1-4]。

潜标水下布放水动力学特性研究具有独特的意义。水下布放相比于水上布放，由于布放点距离锚定点距离相较于水上布放短，省去大量的缆线材料，更加经济实惠。并且由于距离较短，缆绳的自重、外界环境因素如风浪流等带来的影响大大减小，布放环境大大改善，水下布放也更加隐蔽、安全。另外，潜标布放避免了传统的潜标布放方法“标锚法”、“锚标法”定位不准确，大张力载荷受环境影响大等缺点[5]。本次研究的布放方式由于是水下布放受环境因素影响较小，并且由于是在锚和潜标一起下落过程中自行部署释放，几近不再受船只的动负荷冲击。

目前单体式潜标的水上布放的水动力性国内外学者已经做了大量的研究[6-10]。相比单体水上布放，潜标水下布放工程是一个更为复杂的水下系统，包含部署控制释放器等组件，并且极易出现缆线、组件之间的缠结，但是直接进行编程工作量过大，且计算过程较难收敛。本文以大型水动力分析软件OrcaFlex为平台，建立了水下250 m低速流作用下潜标水下布放的动力学分析模型，并对比在各海况下、各工况下对其进行模拟仿真比较。结合水动力性能的计算结果对实际布放工程给出了一些指导性建议。

1 水下布放过程理论基础

1.1 海流理论的选择

潜标系统水动力学分析是要以海流剖面为先决条件，故设计相宜的海流剖面数值是准确计算的前提。为方便分析，对系统水下的工作环境前提和受载荷状况进行合理的简化与假设。(1)因为系统工作期间标体在水下百米处，海面海浪对其作用较小，仅对水下的系统进行动力学研究。(2)设定海流为平面线性流，无垂直分量，简化为二维问题解决。依据有关海流的记录极值和工作状态极值说明[1]，及系统在水下工作的周期，设定了250 m设计海流剖面分布如图1。

1.2 线缆载荷计算

缆索采用凝集质量模型[11]，即由多数无质量的索元和索元中点处的节点组成。将缆线从拖曳端开始离散到系留端共为N段索元，即共存在N+1个节点。只计算索元的轴向和扭转特性，将其模拟成轴向、旋转弹簧与阻尼器的组合体。而节点汇集了两个相邻分段各一半的质量，将各分段上的散布质量效应、外载荷等均分在缆索分段两端的微元节点上。第i分段是指节点i和节点i+1之间的直线弹性元，且每个分段内张力大小相同，方向为该微段的切线方向，微段模型如图2所示。

(1) 缆索张力凝集。

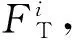
(1)

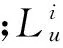
(2) 线缆重力(含浮力)凝集。

(2)

式中：k为Z方向单位矢量。

(3) 缆索微元阻力凝集。

在线缆的局部坐标系下，海流施加在第i段线缆微元上产生的阻尼载荷，认为全部凝聚在单元质量点上，且该载荷包括切向阻尼力和法向阻尼力两部分，则节点上凝集阻尼载荷可表示为

(3)

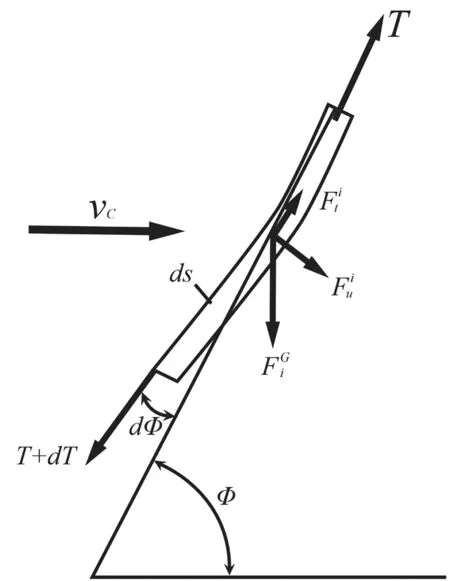
图2 线缆微元段作用力示意图Fig.2 Schematic diagram of force of the cable

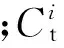
1.3 潜标、锚体的相关环境载荷

潜标系统中潜标在 OrcaFlex中都建模为相同参数六自由度(6D)柱型浮体，即设体积模量无穷大即浮体是不可压缩的，浮体的受力包括重力、浮力、阻力、扭矩、附加质量的作用。海床采用线性海床模型，海床接触力包括法向的穿透阻力、切向的摩擦阻力与切向阻尼。穿透阻力要考虑海床的法向刚度和法向阻尼。OrcaFlex中将锚建模为相同参数的6自由度(6D)方形锚体。在锚体撞击海床的过程中，将海床视为法向线性弹簧模型，海床摩擦阻力满足库伦摩擦力理论，本文取其与海底的摩擦系数μ为0.2。作用于标体上的外力及力矩包含有浮力和重力产生的静水回复力、缆索张力、海水水动力及相对应的的力矩构成，即

F0=FW+FT+FH

(4)

M0=MW+MT+MH

(5)

式中：FW代表静水回复力；FT代表缆绳张力；FH代表作用在标体上的水动力；M是对应的力矩，在环境主要考虑海流的影响，相关力和力矩的计算参考文献[12-13]；有关锚组件的相关计算参考相关文献，本文不再赘述[1]。

2 潜标水下布放过程动力学模型的建立

2.1 布放环境参数

本文选取以下的水流进行研究。采用流函数法(Stream Function Order)为10，波高4.8 m，周期8 s；海流流速符合能量规律：由于海水运动中粘滞性对动量的消耗，流动随深度的增大而减弱，竖直方向二维流速值为从海平面0.1 m/s至海床面为0.075 m/s。该工作海域水温10 ℃，密度恒定值为1.025×103kg/m3，运动粘滞率2.5%，根据实际工程情况选取水深为250 m的海域进行模拟。拖体工作于海床上方100 m。海床法向刚度(kn)、切向刚度均为1 000 kN/m/m2；海床临界阻尼系数(λc)为0。

2.2 模型建立

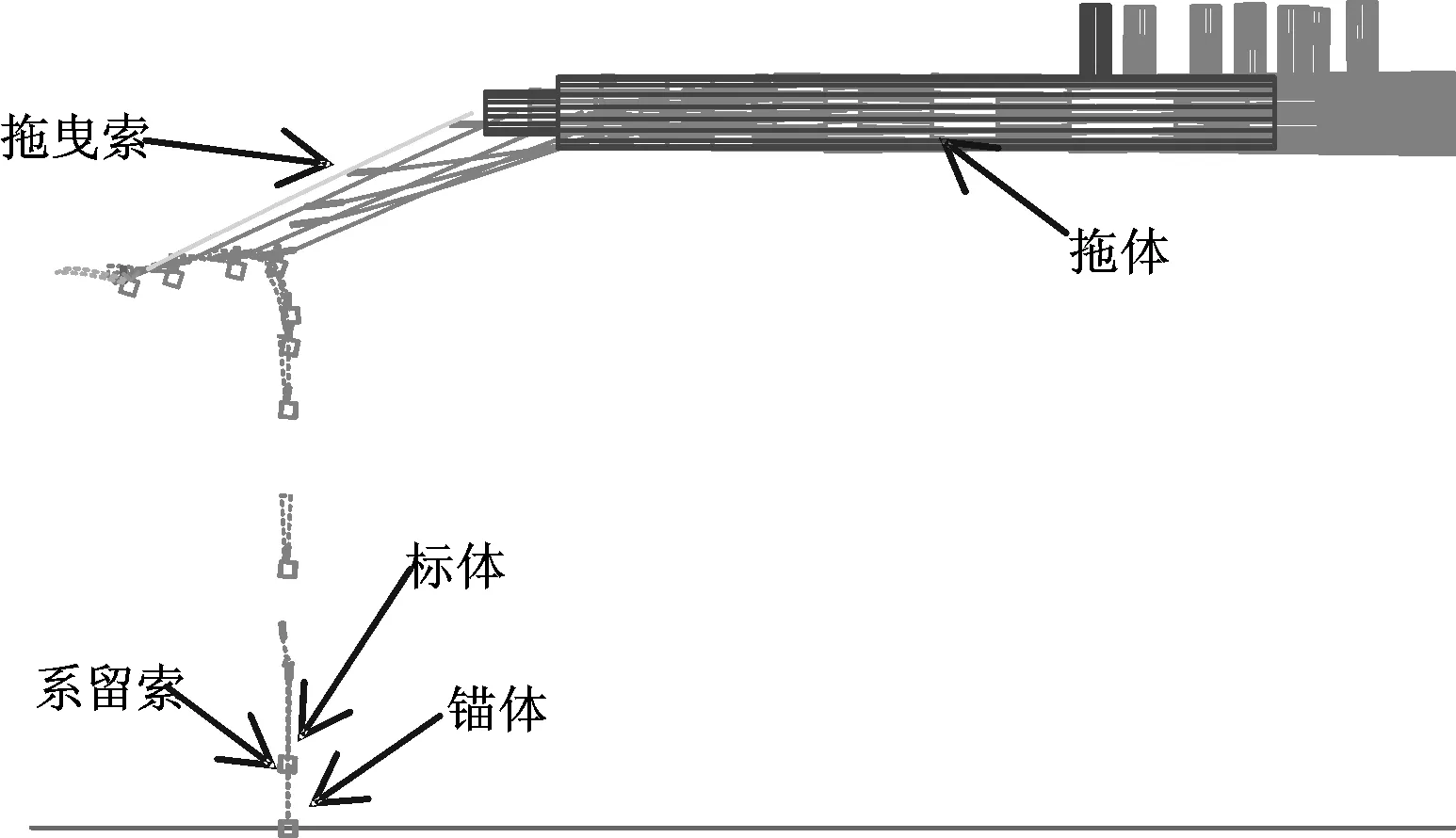
图3 水下布放示意图 Fig.3 Schematic diagram of the deployment

系统模型如图3所示，主要包括潜标主浮体(潜标体)、主系留索、控制开释及锚定系统等。布放过程采用锚标同步布放：作业拖体(Submarine)在海床(Seabed)以上100 m以1.5 m的恒速直航15 s。一条50 m长，半径为0.04 m的拖曳线(Subline)延伸到拖体后面。线的远端连接着由布放器(Deployer)和连杆(Link)组成的释放机构，这些链路能释放锚点。每个传感器组包含定位锚(Anchor)，潜标(Float)和传感器线(Sensor)。在部署前传感器线固定着潜标和锚，并且牵引然后在部署时释放。根据实际布放需要，链接潜标和定位锚的传感器线长20 m，半径均为0.05 m。线缆的密度为1.5 kg·m-1。缆线其他主要参数基本相同，见表1。线缆材料为钢缆(wire rope)，拖曳索(Subline)的弯曲刚度EI为5 kN·m2；EA为轴向刚度，Cdτ、Cdn、Cbd、Caτ、Can、Cab分别是切向、法向、副法向阻力系数和切向、法向、副法向附加质量系数。要注意的是由于锚体在本文设为6自由度，其翻转和回转的上述系数会有所不同，在回转情况时Caτ、Can、Cab均为0；Adτ、Adn、Adb分别为切向、法向、副法向阻力面积，锚体在本模型中均为1 m2。

建立如图3所示模型，各主要模型参数也如表1～表3所示。

表1 线缆主要几何参数表Tab.1 Main geometric parameters of the cable

表2 固定锚的主要物理及几何参数表Tab.2 Main physical and geometric parameters of the fixed anchor

表3 潜标的主要物理及几何参数表Tab.3 Main physical and geometric parameters of the submerged buoy

3 仿真结果

在潜标布放工程中，所要满足的工程条件就是布放的精确性及系统稳定性要求。避免较大的布放误差和过大的潜标标体震荡、线缆的张力剧烈变化等不稳定因素现象出现。仿真系统从不同海况及工况进行潜标水下布放的水动力分析，为具体布放工程的方式选择提供一些参考。

工作状态，首先将系留索和浮标从作业船抛入水中，浮标和系留索入水后在船尾随船当拖曳索基本拉成一条线后，并于作业拖体行驶到预定位置(组件投放点，模型建立于15 s时)依次释放系统，利用系统自身重力定位于锚定点。潜标体于35 s锚件上脱落，模拟时长210 s。

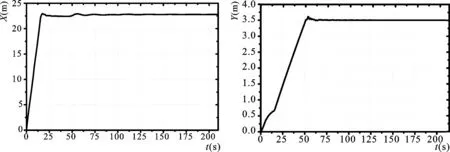
图4 锚的坐标变化时域曲线Fig.4 Time-domain curve of coordinates of the anchor

模拟在稳定低速横流稳定条件下的水下布放过程,作业船以1.5 m的速度直航，0～15 s为系统准备阶段，在T=15 s，x=0 m处进行组件的投放，在T=45 s，组件投放30 s后标体与锚体脱离。图4～图7分别给出锚体定位点坐标曲线、标体运动姿态变化曲线图、全时域内系留缆两端张力变化图和曲率沿缆长方向时域变化图。

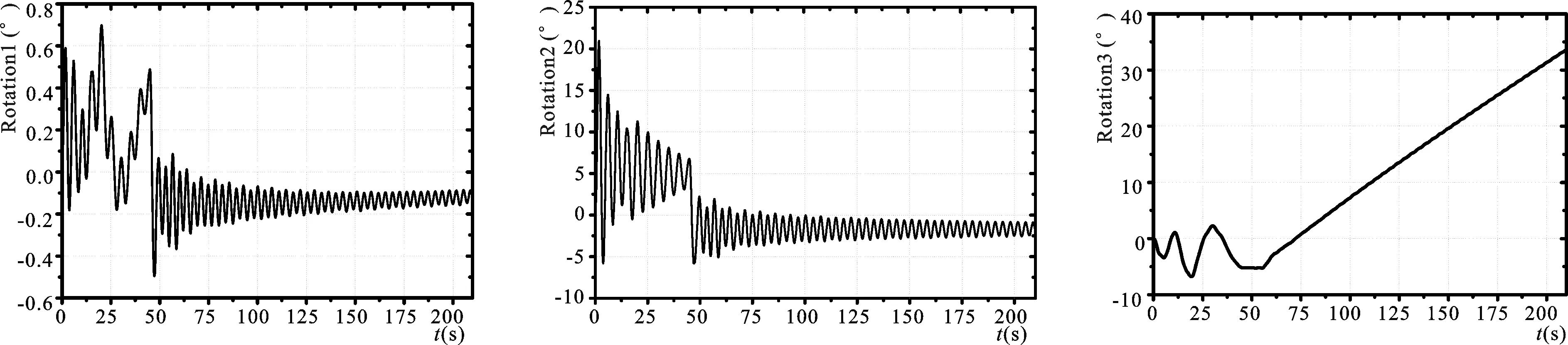
图5 潜标姿态时域变化曲线Fig.5 Time-domain curve of attitude changes of the buoy

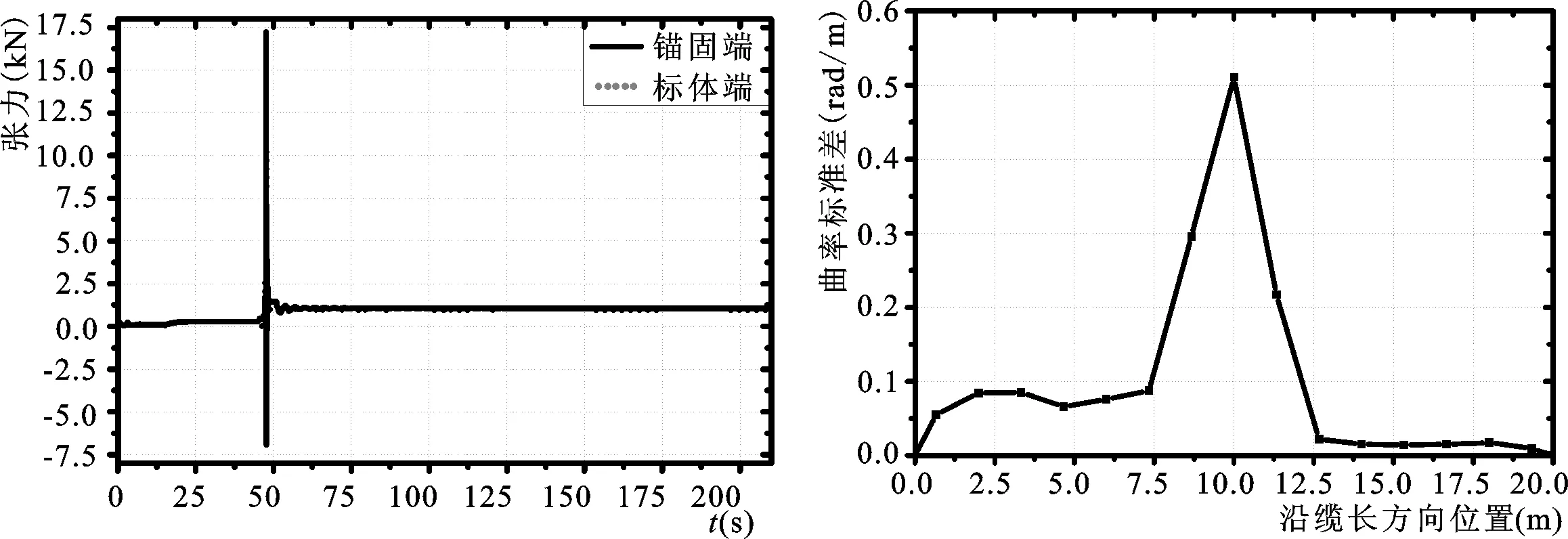
图6 系泊缆两端张力变化曲线Fig.6Time-domaincurveoftensionatbothendsofthemooringline图7 曲率标准差值沿缆长分布曲线Fig.7Distributioncurveofcurvaturestandarddeviationalongthelinelength

由图4可知，在组件随拖体运动期间保持和脱体相同的运动状态，组件投放后，下落过程由于惯性的影响，组件短暂的向前运动一段时间(约为1.6 s)会逐渐向负方向位移一小段距离(约为0.5 m)。这是因为系统所受的法向阻力和大于切向阻力，但是由于X方向海水阻尼的作用，其水平方向的速度基本减小至零并且达到基本稳定状态，故整个下落期间避免常了规标锚法使缆索发生轮形变化产生过大的轮滑效应[6]从而改变锚的运动轨迹；锚地后，在弹性海床和上端标体的联合作用下，锚会发生微小位移并之后逐渐恢复。最终组件于t=48 s，X=22 m附近锚地，即锚位超前投放点22 m。Y方向上变化过程与水平方向变化规律相似。在拖曳期间由于流的惯性力、阻力和拖曳索拖曳力相互作用下，Y方向偏转约0.65 m，布放过程中同样避免了过激的轮滑效应而是简单的线性位移，最终于t=55 s，Y=3.5 m附近锚地。

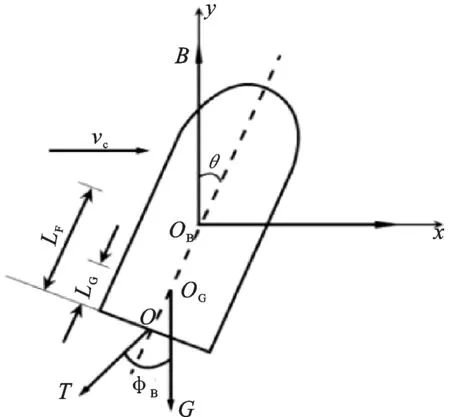
图8 潜标受力示意图Fig.8 Force diagram of the buoy

图5直观描述潜标姿态变化情况，横坐标是工作时间，单位：s，纵坐标是姿态方位，单位(°)。为了方便描述，必须定义所要使用的几个概念和局部坐标系[14]。前后方向用x轴定义，潜标上指向为初始位置时与航向相同的方向；y轴与x轴共处一个平面内；z轴垂直xy平面并且指向向上，绘制如图8所示的坐标系，坐标原点为系留点。潜标体绕各轴的转动分别定义为倾斜(横滚)、俯仰、方位变化(航向、指向)。依照现实工作阶段，将整个布放工序分为3个阶段进行：

(1)标体随组件在拖曳索牵引下随拖体运动阶段；

(2)布放开始至锚触地阶段；

(3)标体姿态变化逐渐稳定并开始工作阶段。

在标体随拖体运动至脱离锚端阶段，即0～45 s时间段内，方位中心最值分别为-0.5°和0.7°，变化周期不明显，周期变长，轴向偏转速率稳定，如图5所示，分析认为是由于组件受海流及微小浪影响及拖体自身的周期的幅度的震动的影响，而在标体工作阶段由于轴向回复力矩小，仅由标体海水阻尼力矩提供，其回复周期很长，轴向偏转速度稳定。如图5所示，潜标在这一期间，倾斜和俯仰方向变化较为有规律，围绕一固定值，且变化幅值在不断缩小，变化周期同样5 s左右，认为是和上述造成方位变化相同的震动因素及标体边界条件引起的；由于转动惯性的影响，经2 s后的相对静止旋转期间后开始向相反方向调整；经约20 s的回复周期后趋于缓和，对应标体自由漂浮阶段；在锚缆张开后锚块下沉间，开始受锚缆的拉力作用，方位变化相对产生规律。标体下沉产生的惯性使系留索松弛，方位变化增大，下沉上浮存在一个震荡周期，并且向着平衡方位逐渐递进。从图可以看出在锚缆张开前这段时间俯仰变化稳定周期性变化并且幅值逐渐减小，在第43 s开始发生锚缆张开，潜标受到较大的拉力作用，从漂浮状态变为底部受拉，俯仰方位变化较大。且同样在锚块触底后，惯性作用下持续下沉，底部拉力消失变为自由漂浮状态，俯仰变化较大。图6同步验证了上述规律。在潜标姿态逐渐稳定阶段内，各个方向上的姿态变化较为平稳，这是由于在此期间海况稳定，柱形潜标主要受缆索的回复力矩M、缆索拉力、扭力和转动时的海流阻力和惯性力的联合作用。

由图6可见，整个布放期间，两端张力随时间变化规律基本保持一致，在拖曳索牵引时，系留索基本不受两端载荷，系留索两端的张力相同几乎为零。布放后直至潜标脱离锚体之前这段时间，两端存在稳定的较小张力，避免了标锚法布放过程中线缆由于锚体自由下落的作用，有效张力不断增加的不利影响。锚触底瞬间，锚与海床瞬间撞击使得挠性系留索瞬间松弛，两端的有效张力瞬间减小呈“负张力”，接着标体上浮使得系留索瞬间拉直造成张力值骤增至最大，并且在之后的一段时间张力值都会出现周期同样约为3s的震荡式变化，且震荡幅度同样逐渐减小，最终在海床法向阻尼作用下最终趋于稳定。

由图7可见，整个布放过程中，系留缆绳的曲率标注差值较有规律(最大值约为0.5)，曲率最大值出现在缆线中间即标体未脱离锚而共同自由下落的过程中出现，故对中段的材料给予重视。

4 参数敏感性分析

4.1 布放深度的影响

分析布放深度对工程结果的影响，实际是分析波浪对实际布放的影响效果。选取拖体工作深度D分别取150 m(波浪影响因子极小忽略不计)、60 m(存在波浪影响)和30 m(波浪影响较大)，波浪方向与海流方向相同。对工程前两过程进行分析比较，结果如图9～图12和表4所示。表中，Ta代表锚的触地时刻，Xa表示锚的X坐标，Ya表示锚的Y坐标，θamax、θbmax和θcmax分别为潜标姿态变化角度的最值，单位为(°)，ωamax、ωbmax和ωcmax分别为潜标姿态变化速度的最值单位为rad/s，F1max、F2max分别为缆索锚固端和潜标端的有效张力的最值，单位为kN，ρmax代表沿缆长方向曲率标准差最大值，单位为rad/m。表中数据不计方向，均取正值。

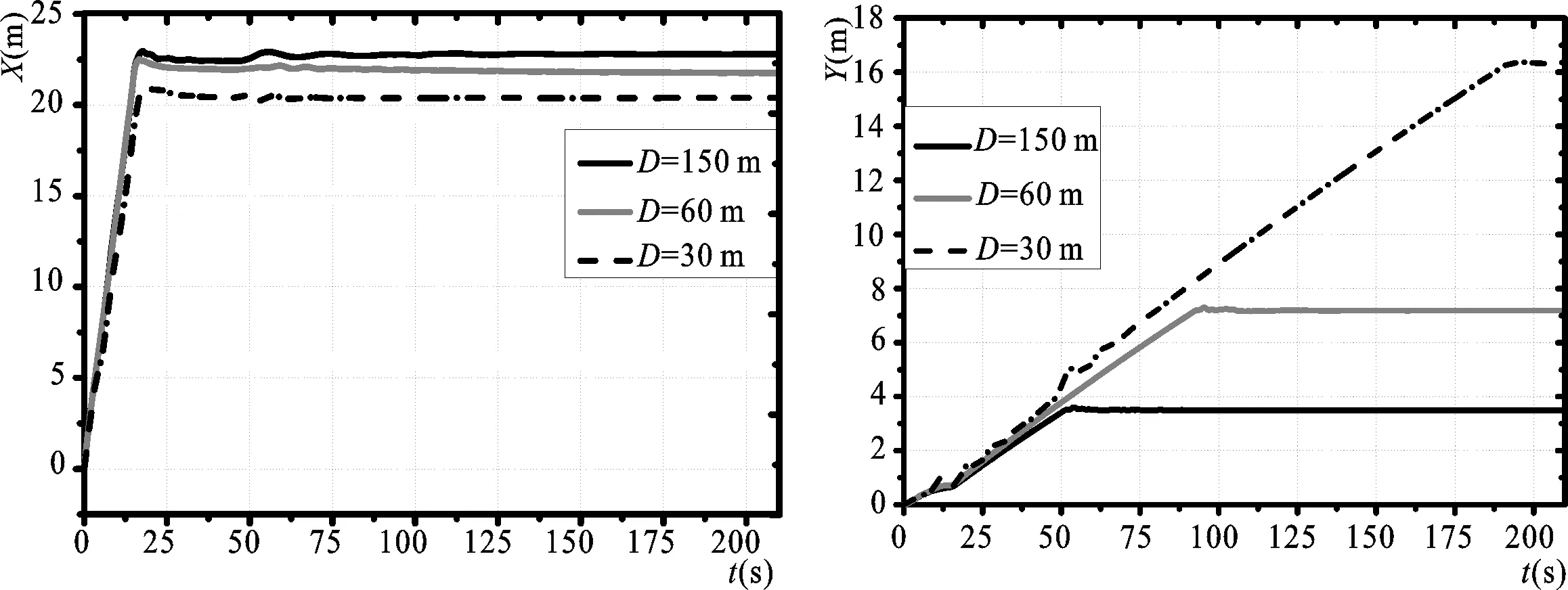
图9 不同深度布放锚体位移时域变化曲线Fig.9 Time-domain curve of displacement of anchors with different depths

从图和表中可知，减小布放深度时，X方向上锚超前运动的距离小幅增加，Y方向上偏移量也增加，并且偏移速度也随之增大。F1max、F2max小幅增加，其他位置的张力最值基本不变；图中在载荷激励作用下的潜标运动姿态变化是：俯仰的姿态变化规律较为明显，曲线围绕着无波浪激励作用时(深度为150 m布放)的姿态变化曲线上下波动，且当波浪激励作用越明显(工作环境越靠近水面)时，波动幅度越大其最值甚至可以达到后者的2倍之多；而倾斜和方位变化剧烈程度一般(倾斜和方位变化的最值出现在触底，此处不予讨论触底瞬间)，这是沿Y轴方向的来流不是产生绕Z轴和X轴的倾角变化的主要原因；尤其注意在改变布放深度因素，各参数并不是完全随着深度的增加而减小，最优的参数布放深度还有待进一步验证。改变工程深度时，姿态变化周期不发生改变，所以同样，潜标姿态变化速度规律同姿态变化相似，另外姿态变化在下沉的过程中剧烈程度逐渐变缓；锚接触海床后，波动逐渐减小，这是因为波浪主要作用在上层海面上、海流速度规律满足线性规律亦随着深度的增加而减小，所以两者的合作用对系统的作用逐渐减弱。由图11、图12可知，布放深度对缆长方向曲率变化影响较小。

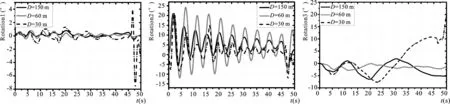
图10 不同深度布放潜标姿态时域变化曲线Fig.10 Time-domain curve of attitude changes of the buoy with different depths

H(m)ta(s)Xa(m)Ya(m)θamaxθbmaxθcmaxωamaxωbmaxωcmaxF1maxF2max15048.820.53.50.7121.56.910.215.320.9917.216.86093.221.87.20.6923.72.920.2316.840.9819.819.730186.522.816.30.9821.97.70.5219.330.9422.321.5

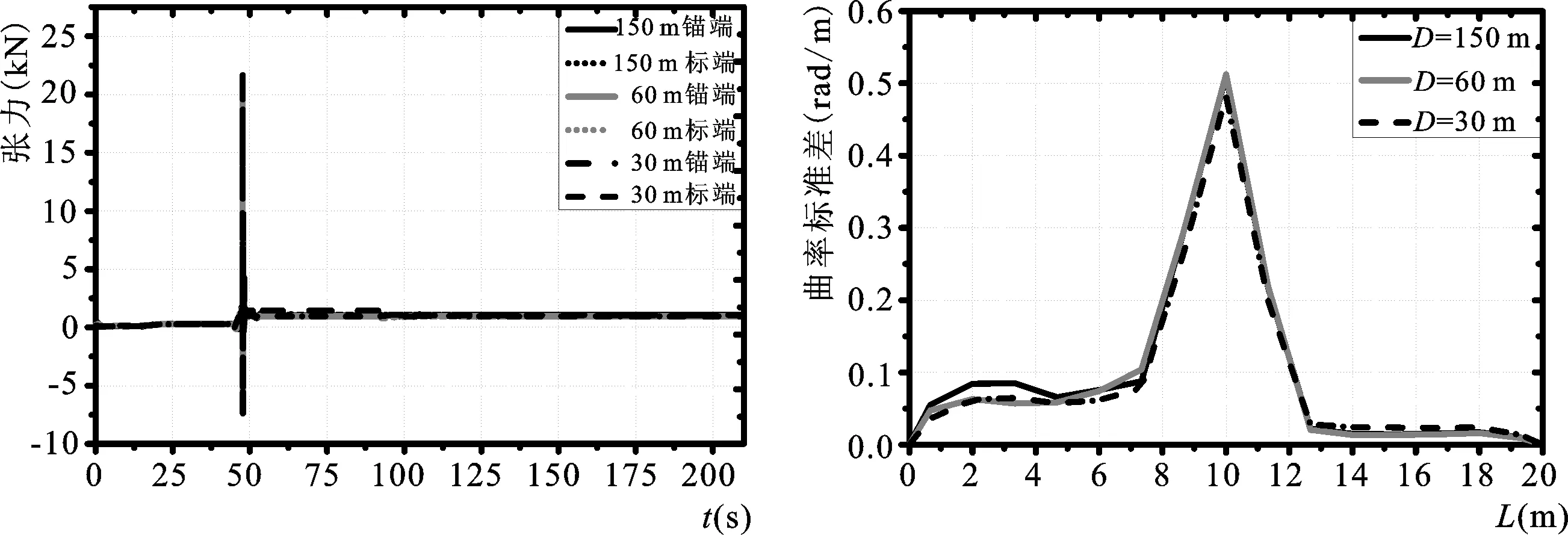
图11 不同深度布放两端张力变化图Fig.11Variationoftensionatbothendsofthelinewithdifferentdepths图12 不同深度布放曲率标准差沿缆长分布图Fig.12Distributioncurveofcurvaturestandarddeviationalongthelinelengthwithdifferentdepths

4.2 速度的影响

图13 不同航速布放的锚坐标时域变化曲线Fig.13 Time-domain variation curve of anchor coordinates at different deployment speeds

作业拖体沿着X正方向运动，为系统提供了初始X方向的运动初速度矢量，横向流(Y轴正方向)则为系统提供了偏移速度，在探究速度对系统受力影响时，忽略波浪的影响。图13～图16以及表5分别列出了仅改变船速为1.5 m/s、0.5 m/s和2.5 m/s和仅改变海面流速为0.1 m/s、0.5 m/s和1 m/s时的模拟结果。结果可见，初始布放速度的改变会改变锚位与投放点的水平距离，布放初速度越大，X方向超前距离越大且几乎成正比增大。当速度每增加1 m/s时，Y方向上的偏移会小幅度增加(增幅约为5%)。当深度、横流方向一定，不同初始布放速度下，潜标在布放阶段的三方位姿态变化不明显，其偏转角度和最大偏转速度几乎没有受到影响，但是在锚地后的稳定阶段，绕Z轴的旋转不管是方向或是偏转速度却都会出现区别。从图和表中可见，初始布放速度的变化对系泊索两端张力不产生影响；低航速布放时速度变化不影响缆长方向的曲率最大值且都出现在缆线中段，但是当航速提高到一定时，缆绳全长范围内的曲率值都在增加，这是因为系统与海流的相对速度增大到一定值时，缆绳流阻力增加，而标体和锚体还互相固定，缆绳几成张紧弯折状态。

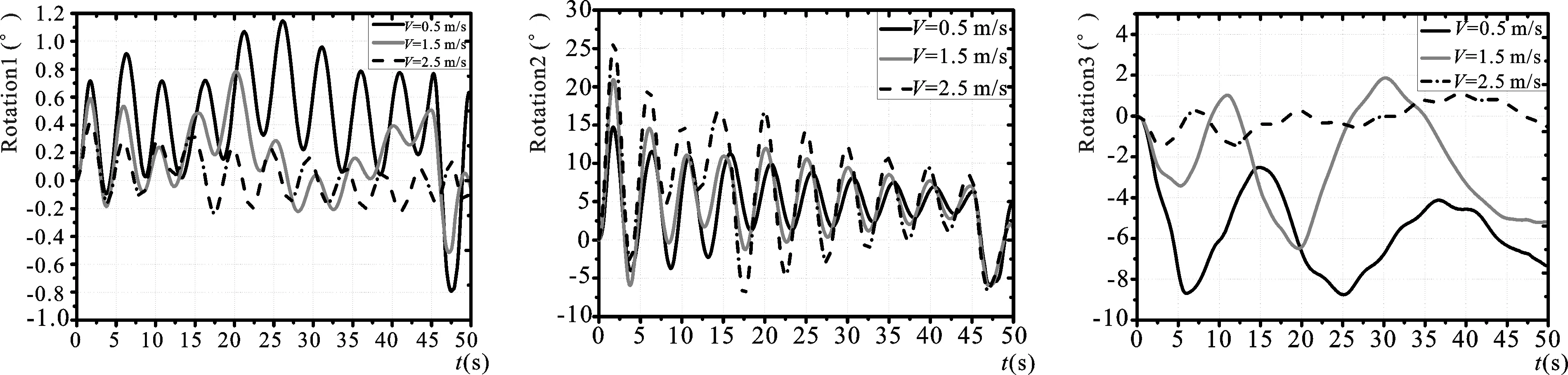
图14 不同航速布放的潜标姿态变化时域变化曲线Fig.14 Time-domain curve of attitude changes of the buoy at different deployment speeds

V(m/s)ta(s)Xa(m)Ya(m)θamaxθbmaxθcmaxωamaxωbmaxωcmaxF1maxF2max0.548.29.13.21.1514.18.700.6310.031.4717.216.81.548.821.83.50.8121.96.580.4113.950.8917.016.82.549.535.43.70.4226.21.740.2314.230.2916.916.7

如图17～图20可知，而当横流方向上的流速依次增大时，Y方向上的锚地点发生Y正方向上的偏移，且迎流面速度的增加直接造成流阻力系数的增大从而造成流阻力载荷作用明显，标体下端边界条件受系留索束缚，上端呈自由边界状态，故造成潜标俯仰方向姿态稳定性受到破坏，θbmax、ωbmax变大。其他模拟结果基本不受流速影响。

图15 不同布放速度的两端张力时域变化曲线Fig.15Time-domaincurveoftensionatbothendsofthelineatdifferentdeploymentspeeds图16 不同布放速度的曲率标准差沿缆长方向变化曲线Fig.16Distributioncurveofcurvaturestandarddeviationalongthelinelengthatdifferentdeploymentspeeds图17 不同流速布放锚坐标时域变化曲线Fig.17Time-domaincurveofanchorcoordinatesatdifferentcurrentvelocities

图18 不同流速布放标体姿态时域变化曲线Fig.18 Time-domain curve of attitude changes of the buoy at different current velocities

V(m/s)ta(s)Xa(m)Ya(m)θamaxθbmaxθcmaxωamaxωbmaxωcmaxF1maxF2max0.148.822.53.50.7121.18.620.4812.960.9517.216.80.548.922.517.23.3520.929.14.6312.844.5517.316.71.049.122.829.35.7220.938.55.8213.338.5417.316.5

图19 不同流速两端端张力时域变化曲线Fig.19Time-domaincurveoftensionoftheanchoratdifferentcurrentvelocities图20 不同横流速的曲率标准差沿缆长方向时域变化曲线Fig.20Time-domaincurveofcurvaturestandarddeviationalongthelinelengthatdifferentcurrentvelocities

4.3 布放方向与流向夹角的影响

实际工作环境海域中，系统初速度方向与流向之间的夹角变化必然使得系统受到作用出现明显变化。对此，深水布放忽略波浪作用，其他条件一定，分别选取夹角分别为0°、90°、180°三个方向进行分析。

结合表7和图21～图24观察可知，夹角的变化对于锚定点位置的影响较大，0°、45°、90°、135°、180°下的X方向超前运动依次减小，反向时，系统与来流相对速率最大，切向速度与法向速度的差值最大。系统从拖曳线自动释放后，滑轮现象最为明显；系统从Y方向偏移量先增大再减小，这是由于流体实际作用阻尼在90°是最值的原因。

图21分别为不同初速度方向和流向夹角情况下潜标姿态变化情况，结合表7可见，在流速较低的情况下，当流向逐渐向速度方向垂直过程中，潜标下边界始终受到缆线轴向张力束缚，轴向张力与下端界面法向阻尼、升力动态抵消，俯仰姿态不发生明显变化，并且之后逐渐浮力与张力平衡，俯仰姿态达到稳定。在流向逐渐向初始速度方向垂直过程中，来流速度一定时，海流作用在潜标体上的海流力分解成的法向阻力逐渐增加和切向阻力逐渐减小，故在此过程中，倾斜姿态变化逐渐加剧，θamax、ωamax在横流时达到最值；由于缆绳下端系留点不在中心，缆绳作用在标体的回复力矩、扭力和海水动力和相应力矩在X方向上相互影响，动态载荷相互抵消，由于在相对速度恒定的情况下，切向水动力逐渐减小，标体切向载荷减小，方位变化减弱，θcmax、ωcmax于横流时最小。并且由于初始系留索对下界面的扭力矩的作用下，在缆绳扭矩方向与水动力矩方向一致(迎流布放)时，θcmax、ωcmax达到最大值，方位变化最为剧烈，此时对潜标的姿态稳定要求和缆绳抗扭要求最高。在流速变大时，上述特征表现得更加明显。由图24可见，流速、流向对系留索两端张力和曲率沿缆长的改变几乎没有影响。

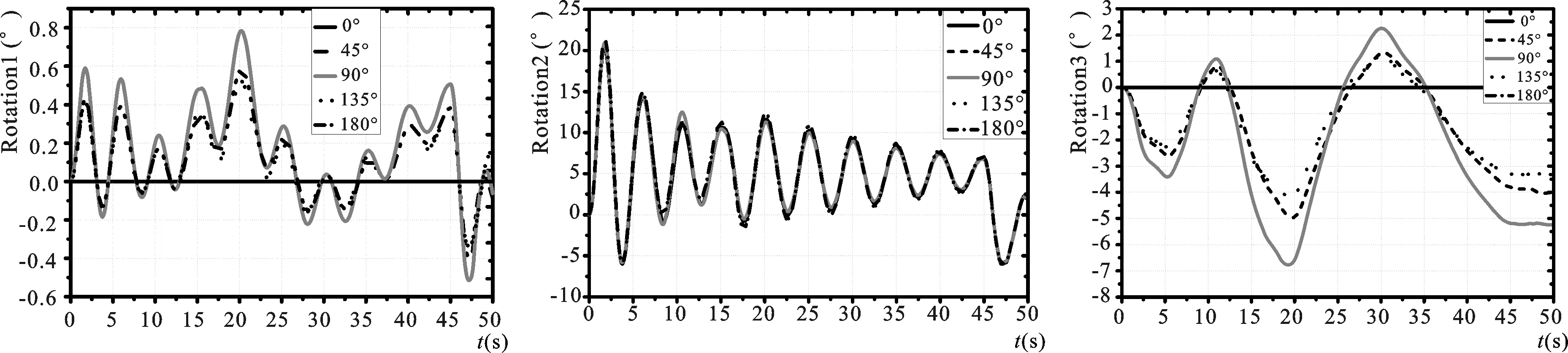
图22 不同流向布放阶段潜标姿态时域变化曲线Fig.22 Time-domain curve of attitude changes of the buoy at different current directions

A(°)ta(s)Xa(m)Ya(m)θamaxθbmaxθcmaxωamaxωbmaxωcmaxF1maxF2max051.125.50022.100.046.960.0317.216.84551.124.12.50.5922.254.636.840.6317.216.79051.223.33.50.7822.16.855.827.030.9517.216.813551.119.42.50.5122.14.124.566.990.5917.116.818051.218.70022.000.037.000.0217.216.8

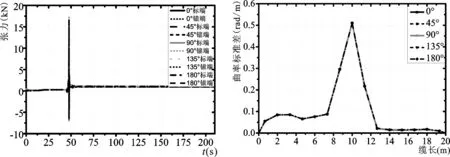
图23 不同流向时两端张力时域变化曲线Fig.23Time-domaincurveoftensionoftheanchoratdifferentcurrentdirections图24 不同流向时曲率标准差沿缆长方向时域变化曲线Fig.24Time-domaincurveofcurvaturestandarddeviationalongthelinelengthatdifferentcurrentdirections

4.4 弯曲刚度影响

线缆的材料对系统工况会产生影响，为探究弯曲刚度对布放过程的结果影响，本文选取系留索的弯曲刚度分别为0、102kN·m2和102kN·m2三种刚度值。图25～图28和表8给出三种情况下的计算结果。

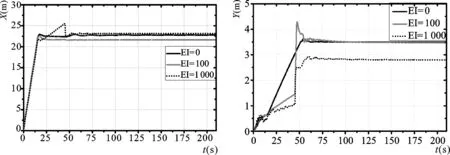
图25 不同系留索弯曲刚度锚坐标时域变化曲线Fig.25 Time-domain curve of anchor coordinates with different bending stiffnesses

如图25所示，当考虑了系留索的弯曲刚度后，横流作用下，系统触地时间、锚落地点超前距离无明显改变，但是当刚度增加到一定值(1 000 kN·m)时，触地偏移距离会变小，这是由于此类特定的布置法使得系统在整个过程中都是一个整体，超前距离不存在应刚性管线弯曲变形程度改变而产生系统布放定位大偏差，但是横流作用下，刚性线缆几成直线状态而在Y方向上偏移速度减小。从图26可知，由于刚性线不易弯曲、弯曲变形后产生的力矩会急剧增大，刚性管线对潜标布放过程中的三个运动姿态稳性都会产生剧烈影响，且刚度越大，标体运动姿态变化越剧烈，也就是标体稳定性越低，并且在拖曳时期的的姿态变化加剧。注意到，在系统布放下落过程中，刚性缆绳构件减小了锚体与弹性海床的撞击影响，所以在锚触地瞬间系留索产生的交替式张紧-松弛效应得到减弱，系留索两端张力最大值随着刚性增大而减小，但是考虑刚度后，全程张力变化频繁，这点在坐标曲线和潜标姿态变化图均有体现，系留索两端张力最值出现在随船拖曳阶段而不是标锚分离缆绳张紧瞬间；并且稳定状态的张力值也同样略微降低。另外刚性缆绳也大大降低了系留索全长方向的曲率变化激烈程度。

图26 不同系留索弯曲刚度潜标姿态时域变化曲线Fig.26 Time-domain curve of attitude changes of the buoy with different bending stiffnesses

EIta(s)Xa(m)Ya(m)θamaxθbmaxθcmaxωamaxωbmaxωcmaxF1maxF2max048.822.63.500.7120.78.70.4811.960.5517.216.810048.622.03.5098.265.316234.768.423.912.612.3100047.322.72.8261388.7119658419336418.98.5

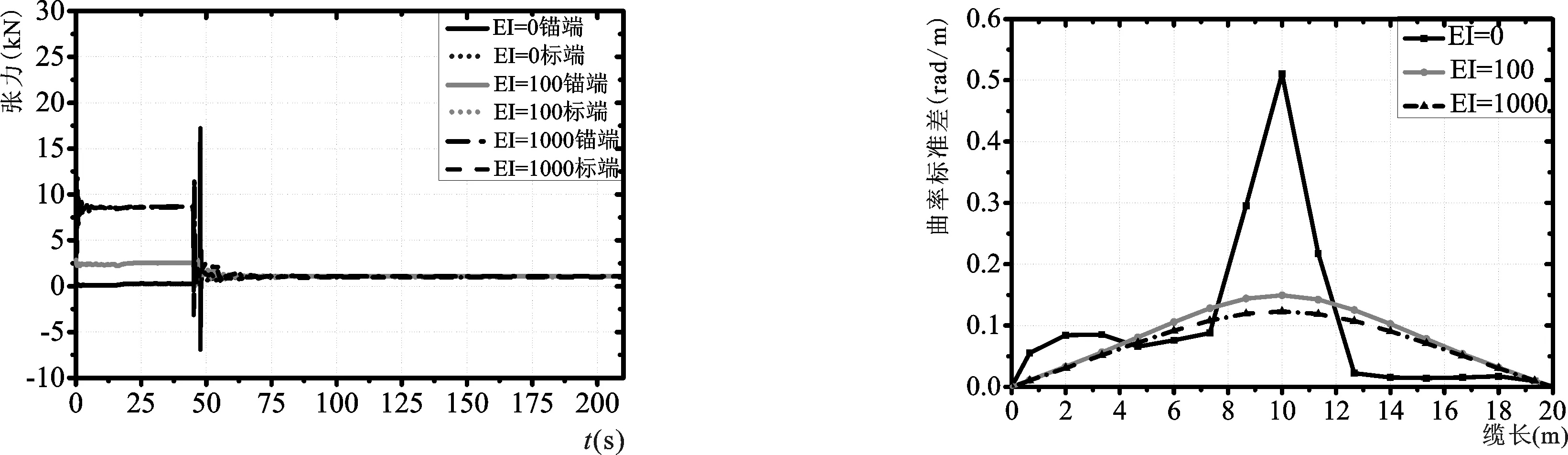
图27 系留索刚度不同时两端张力时域变化曲线Fig.27Time-domaincurveoftensionoftheanchorwithdifferentbendingstiffnesses图28 系留索刚度不同时曲率标准差沿缆长方向分布曲线Fig.28Distributioncurveofcurvaturestandarddeviationalongthelinelengthwithdifferentbendingstiffnesses

5 结论

潜标系统的初始设计和水下布放效果会很大程度受到布放过程中水动力性能的影响，基于对此新型布放法的时域模拟结果和分析，可以得到以下结论：

(1)在作业拖体的作用下，系统在投放后的顺势横向位移主要取决于其拖曳阶段的运动速度也就是航行速度及航向和流向之间的夹角有关，而其他因素的改变对横向定位影响较小；纵向定位主要取决于水流的横向载荷及系统自由下落的时间，另外，相同条件下，弯曲刚度的增加会轻微减少下落的时间从而减小纵向偏移。因此，潜标系统的定位主要由作业船的运动决定。

(2)横向布放过程中，影响标体姿态变化的因素很多：不同作业水深对潜标的倾斜、方位变化不明显，但在某一水深处标体会产生较明显的俯仰变化，猜想是潜标在此时受流速和作业船速共同激励下发生某种共振而造成的；低速横流下，作业船速度降低之后，此时的共振现象愈明显，潜标姿态稳定性越差。故水下布放的工程速度并不是越低越好，若低于某一值后，反会伤害系统稳定性；其他条件一定时，工作环境流速的增加对标体姿态变化尤其是方位变化影响较大，流速越大，后者越不稳定，建议低流速环境下进行作业；若计入系留索刚度后，在缆绳的强大力矩作用下，潜标姿态变化完全超出其所搭载的仪器设备的安全和工作要求，故建议系留索采用柔性缆绳。此外，航向与流向的夹角的改变会影响到潜标的姿态变化，但不超过其姿态变化要求。

(3)布放过程中，系留索的张力峰值在锚触地后到达峰值，在其他时间内张力较小，锚固端的张力始终大于潜标端；除系留所本身的刚度外的因素对线缆张力影响都很小，在计入线缆弯曲刚度后，系留索的张力整体降低，触地时间略微微减小。系留索的曲率变化在中段变化最为剧烈，故在线缆中段要进行抗扭加强；但在刚性材料力矩作用下，其变化程度有明显减弱，但综合第二条结论考虑，仍建议系留索采用中段抗扭加强的柔性缆绳材料。

参考文献：

[1]王明午.海洋潜标系统的静力分析和姿态计算[J].海洋技术学报, 2001, 20(4):41-47.

WANG M W. Static Analysis and Attitude Calculation of Marine Submersible Buoy System[J].Journal of Ocean Technology, 2001, 20(4):41-47.

[2]863计划海洋领域海洋监测技术(818)主题办公室.海洋环境监测及其卫星-浮标、潜标技术[C]//世纪初海洋监测高新技术发展战略研讨会论文集.北京：海洋出版社,2000:13-19.

[3]王婷.国外海洋潜标系统的发展[C]// 中国声学学会水声学分会.2011年全国水声学学术会议论文集.上海:声学技术,2011:324-326.

[4]杨永春，张会杰, 田伟辉,等.海流作用下潜标-系留系统耦合动力响应试验研究[J]. 海洋技术学报, 2012, 31(3):1-5.

YANG Y C,ZHANG H J,TIAN W H, et al.Experimental Research on the Coupling Dynamic Characteristic of Submersible Buoy-Mooring System under the Ocean Current[J].Journal of Ocean Technology,2012, 31(3):1-5.

[5]杨坤汉，王明午.绷紧型单点锚定潜标系统布放回收操作方法[J]. 海洋技术学报, 1989(1):51-69.

YANG K H,WANG M W.Approach of Deployment/Reeovery for A Single-Point Taut Subsurface Mooring System[J].Journal of Ocean Technology, 1989(1):51-69.

[6]张洋，朱克强.海洋潜系统布放动力学分析[J]. 船舶工程, 2014(2):111-114.

ZHANG Y, ZHU K Q. Dynamic Analysis of Deployment of Oceanographic Subsurface Buoy System[J]. Ship Engineering, 2014(2):111-114.

[7]葛德宏, 朱海, 高大远,等.深海潜标布放运动与定深控制策略研究[J]. 舰船科学技术, 2016, 38(13):87-90.

GE D H,ZHU H,GAO D Y, ea al. Research on laying motion simulation and depth control of deep-sea submerged buoy[J]. Ship Science and Technology,2016, 38(13):87-90.

[8]倪佐涛, 姜静波, 徐永平,等.一种适用于石油平台的有缆潜标系统的设计与布放方法[J]. 海洋科学, 2012, 36(12):81-83.

NI Z T, JIANG J B, XU Y P, et al. A design and deployment of mooring wired-buoy system for offshore jacket platform[J]. Marine Sciences, 2012,36(12):81-83.

[9]Chang Z Y,Tang Y G,Li H J,et al. Analysis for the Deployment of Single-Point Mooring Buoy System Based on Multi-Body Dynamics Method[J]. China Ocean Engineering ,2012, 26(3):495-506.

[10]Zheng Z Q, Dai Y, Gao D X, et al. Dynamics of Deployment for Mooring Buoy System Based on ADAMS Environment[J]. Advanced Materials Research, 2013, 819:328-333.

[11]朱克强, 李道根, 李维扬,等. 海洋缆体系统的统一凝集参数时域分析法[J]. 海洋工程, 2002, 20(2):100-104.

ZHU K Q, LI D G, LI W Y, et al. Lumped-parameter analysis method for time-domain of ocean cable-body systems[J]. Ocean Engineering, 2002, 20(2):100-104.

[12]黄志. 福建沿海船舶事故的灰色关联分析[J]. 上海海事大学学报, 2006, 27(1):21-25.

HUANG Z. Grey Incidence analysis on maritime accidents along Fujian coast[J]. Journal of Shanghai Maritime University, 2006,27(1):21-25.

[13]范中洲, 吴兆麟, 张闯,等. 基于可拓理论的船舶定线制应用研究[J]. 大连海事大学学报, 2013, 39(1):43-45.

FAN Z Z, WU Z L, ZHANG C, et al. Application research of extension set theory in ship′s routing [J]. Journal of Dalian Maritime University, 2013, 39(1):43-45.

[14]侯广利, 张颖, 孙继昌,等. 一种潜标的水下姿态变化规律分析[J]. 海洋技术学报, 2010, 29(3):38-43.

HOU G L, ZHANG Y, SUN J C, et al. Analysis of Attitude Variation for Submersible Buoy System[J]. Ocean Technology, 2010, 29(3):38-43.