基于液压管接头接触面密封性能及螺纹受力分析的研究

张 慧，高云林, 宋高瑞

(西南石油大学 石油与天然气工程学院，四川 成都 610500)

0 引 言

锥面密封和球面密封是在轴向力的作用下产生密封比压的一种密封方式，因其工作时密封面上不易存积硬杂物，且在相同的轴向力作用下比平面密封的比压更大[1]。因此，液压管接头和公称直径较小、高温高压工况的阀门中常采用锥面或球面密封。保证密封性能的因素有很多，包括温度、工作压力、工作介质等，其中密封面的接触应力和密封宽度对密封性能有重要影响[2-4]，笔者基于这两大因素展开锥面密封和球面密封的密封性能研究的。ABAQUS是一套功能强大的有限元分析软件，其解决问题的范围从相对简单的线性问题到复杂的非线性问题，大量复杂的非线性问题可以通过不同的组合很容易模拟出来。运用ABAQUS软件，通过改变设计参数得到最佳的设计方案，从而缩短设计周期，减少设计阶段人力、物力的投入[5]。笔者以某型液压管接头模型为例，运用ABAQUS软件分析锥面密封和不同弧面半径的球面密封模型在螺纹预紧力作用下的密封性能，同时分析了连接螺纹取不同圈数时螺纹牙的受力情况，从而为锥面密封和球面密封以及其连接螺纹的设计提供一定的指导和借鉴。

1 密封结构

笔者以常用60°液压管接头为研究对象，研究液压管接头常采用的锥面密封或球面密封方式。锥面密封和球面密封结构相同，主要由阀体、阀座组成，如图1所示。阀体和阀座通过螺纹连接，通过拧紧螺纹产生一定的预紧力使阀体的密封面与阀座的密封面紧密贴合实现密封。锥面密封的密封面是两端部为60°锥面，接触方式为面-面接触，如图2(a)所示。球面密封的阀体密封面是半径R的弧面，阀座密封面是60°锥面，初始接触方式为线-面，如图2(b)所示。

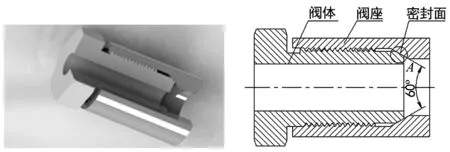
图1 密封结构

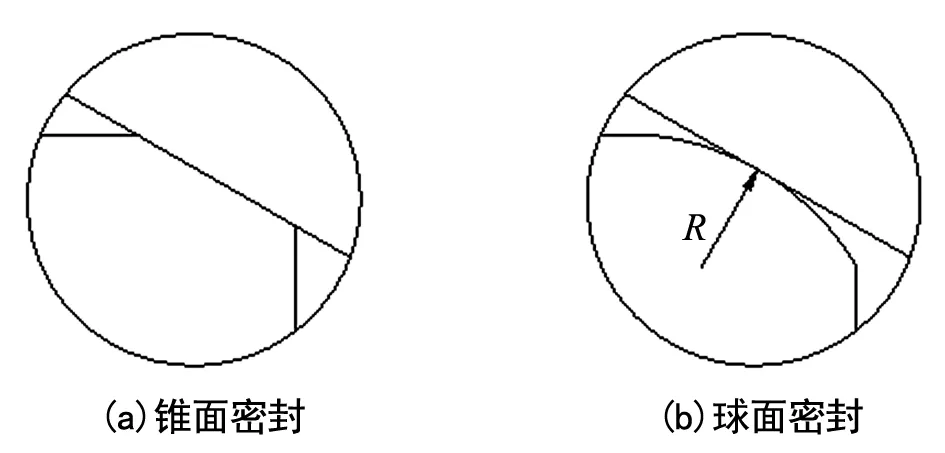
图2 A区域放大图

2 有限元模型建立

由于考虑螺纹升角的三维模型在有限元模拟中计算量大，又因为密封结构和载荷具有对称性，因此本文忽略螺纹升角影响采用二维模型的一半进行仿真分析。建立了锥面密封、不同弧面半径球面密封、不同圈数连接螺纹的密封结构模型，对模型进行有限元仿真，研究锥面密封的密封面应力分布和不同弧面半径对密封性能的影响，以及螺纹牙的受力情况，分组建模参数如表1所列。

表1 建模参数

2.1 定义接触

锥面密封和球面密封在实现密封的过程中是状态非线性(密封面的接触、螺纹的接触)和材料非线性(接触面的弹塑性变形)并存的过程[6]。非线性接触问题与弹塑性有限元问题一样，其定解条件包括有限元平衡方程、边界条件、材料本构模型、摩擦模型以及接触约束条件等。其中接触条件包括 3 种状态，即分离、粘合、滑动，对于粘合和滑动状态接触面的位移必须满足非穿透条件[7-8]：

nTΔu-g≤0

(1)

式中：Δu为接触体间相对变位矩阵；n为接触面法线向量；g为初始接触间隙。

弹塑性接触分析的最小位能原理为：在所有满足求解区域内的应力-应变关系和位移边界条件的可能增量位移场中，其真实解使弹塑性系统的总位能取最小值：

(2)

式(2)的矩阵形式表示为：

(3)

式中：u为变位矩阵；K为刚度矩阵；F为节点载荷向量。

接触面之间的相互作用包含两部分：①接触面的法向作用；②接触面的切向作用，切向部分包括接触面间的滑动摩擦力[9]。模拟真实的摩擦行为是非常困难的，ABAQUS仿真分析时使用一个允许“弹性滑动”的罚摩擦公式。定义阀体的螺纹牙和密封面为主接触面，阀座的螺纹牙和密封面为从接触面，螺纹牙间的摩擦因数为0.12，密封面间的摩擦因数为0.05。

2.2 施加载荷

如图3所示。在阀座的左右两个表面施加固定约束，对阀体的上下表面施加位移约束，限制其y方向位移。在阀体左端沿x方向施加260 kN拉力模拟螺纹预紧力。

图3 施加载荷

2.3 网格划分

如图4所示。对模型网格划分采用的单元类型为非协调模式单元C3D8I，它把增强单元位移梯度的附加自由度引入线性单元，能克服线性完全积分中的剪切自锁问题，具有较高的计算精度。为了得到更精确的结果，将接触面的网格做加密处理，主接触面的网格局部尺寸设为0.02 mm，从接触面的网格尺寸设为0.01 mm。

图4 网格模型

3 结果分析

3.1 锥面密封受力分析

图5是锥面密封结构在螺纹预紧力作用下的应力分布，图6是密封面的应力云图。

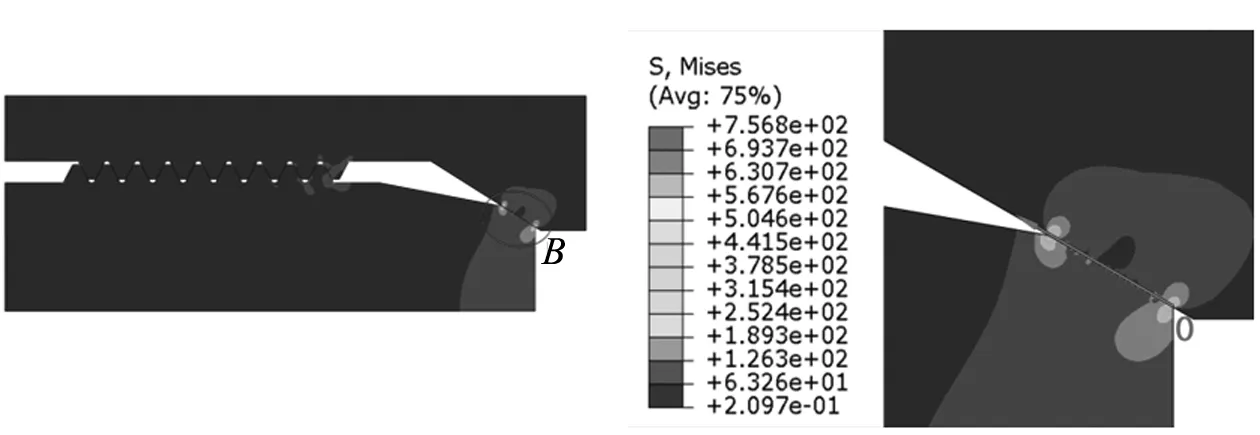
图5 锥面密封结构应力云图 图6 B区域应力云图

图7是沿图6箭头方向密封面的接触应力分布曲线。从图7可以看出，锥面密封结构密封面的接触应力分布曲线呈U型，接触应力峰值出现在两端位置，中间应力值在100 MPa左右浮动。接触面的最大接触应力值达到700 MPa，中间的最小应力值只有61 MPa，平均接触应力值135 MPa，最大值是最小值的11倍。两端的接触应力值虽大，但接触面的宽度很小，锥面密封主要靠中间应力值相对较小但宽度长的部分实现密封。

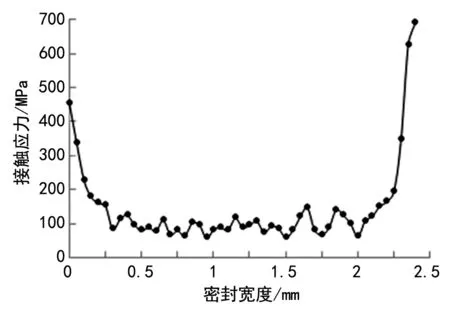
图7 密封面接触应力分布曲线

3.2 球面密封受力分析

通过对不同弧面半径球面密封结构模型的分析，得到了不同弧面半径的密封面接触应力分布情况，以及密封宽度和平均接触应力与弧面半径的关系。

图8是不同弧面半径对应的平均接触应力值，图9是不同弧面半径对应的密封宽度。由以上两图可以看出，随着弧面半径的增大平均接触应力值不断下降，密封宽度不断增加。但当弧面半径增大时，接触应力的下降幅度和密封宽度的增加幅度都在不断降低，弧面半径大于80mm时，平均接触应力值的降低趋势和密封宽度的增加趋势都明显变缓，且逐渐趋于平稳。

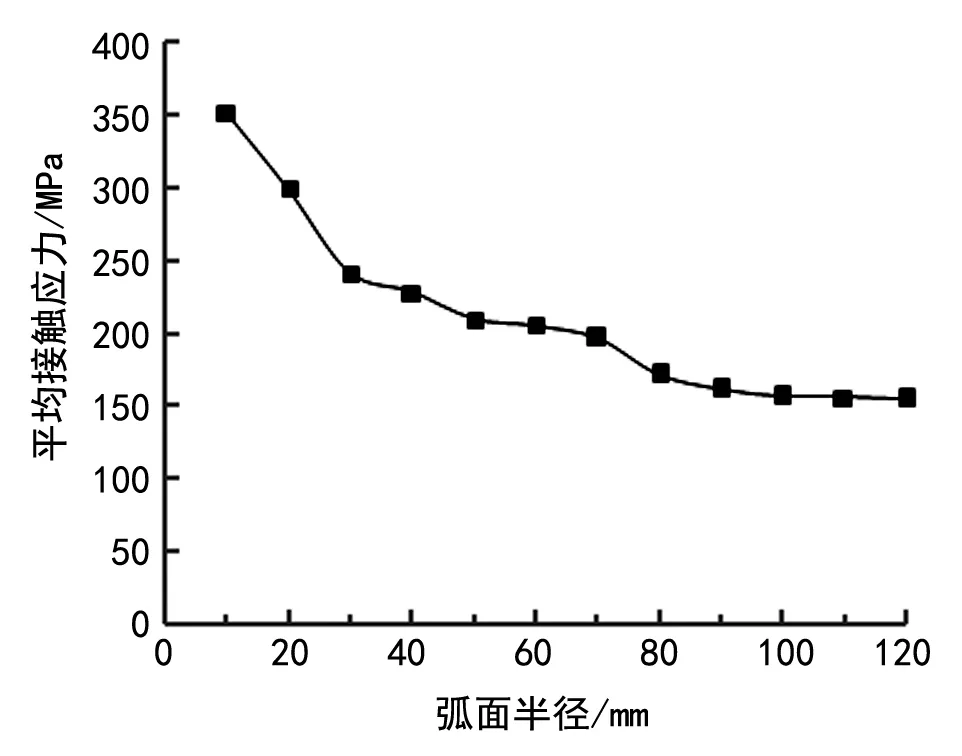
图8 平均接触应力随弧面半径变化曲线

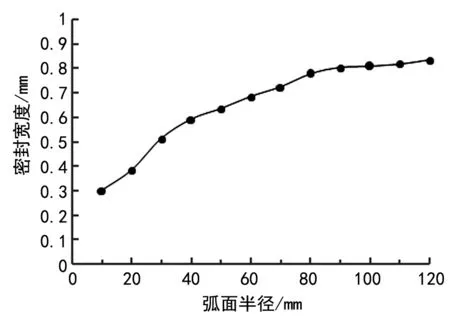
图9 密封宽度随弧面半径变化曲线

以上分析了弧面半径为20 mm、40 mm、70 mm和100 mm球面密封模型密封面的应力分布情况。图10是不同弧面半径密封面的接触应力云图。图11是以弧面与锥面的相切点为原点，沿图10(a)坐标所示方向，不同弧面半径密封面的接触应力分布曲线。从图11可以看出，弧面半径小的接触应力分布曲线的中间部分在弧面半径大的接触应力分布曲线之上，即弧面半径越小，密封面中间部分的接触应力值越大。弧面半径较小时，应力分布曲线呈单峰，最大应力值出现在弧面与锥面相切点附近，沿原点(相切点)向两端延伸接触应力值下降较快，如弧面半径为20 mm和40 mm的接触应力分布曲线；弧面半径增大到一定值后，应力分布曲线呈双峰，最大接触应力值并未出现在原点(相切点)附近，而是向密封面两端靠近，如弧面半径为70 mm和100 mm的接触应力分布曲线。

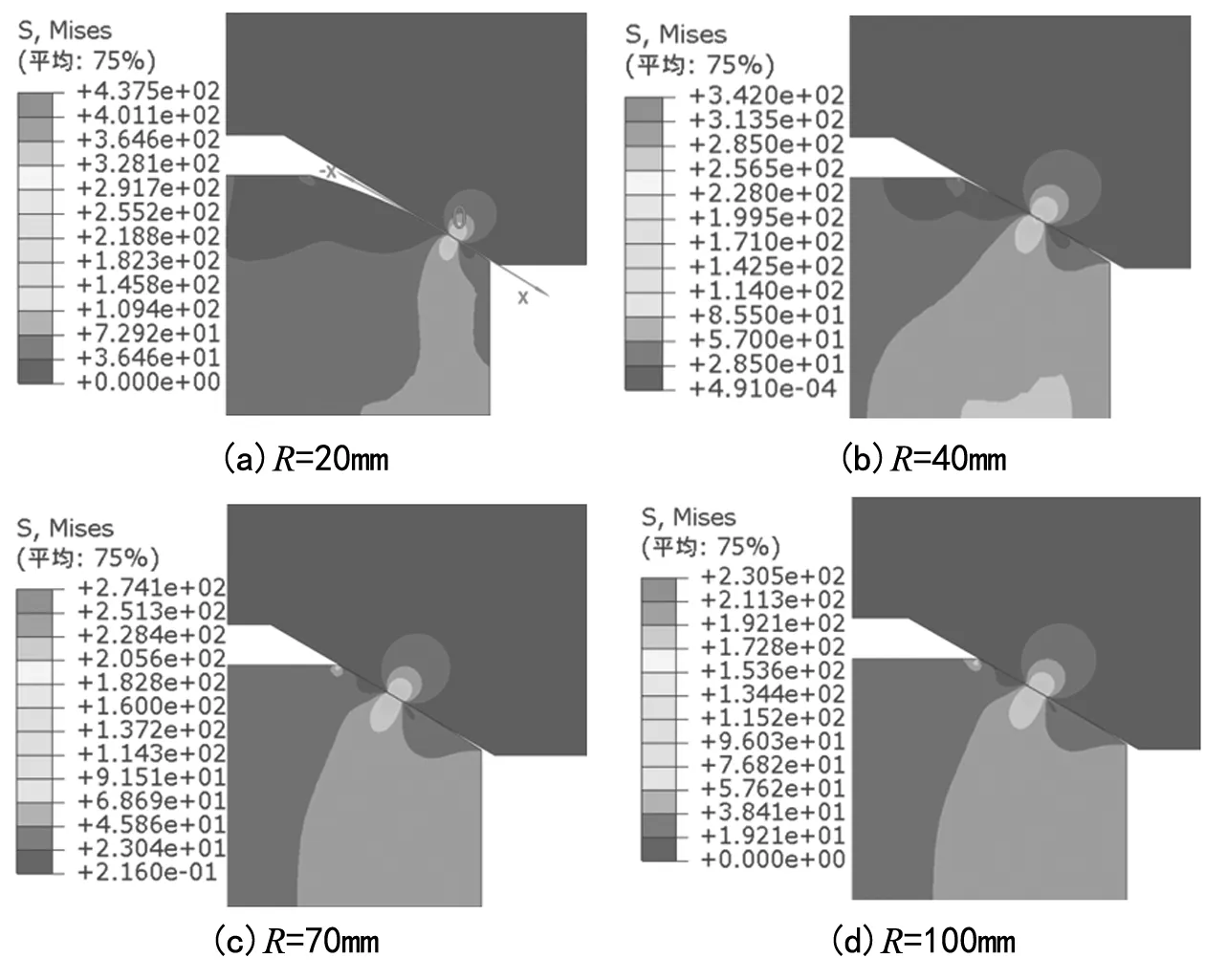
图10 不同弧面半径密封面应力云图

图11 不同弧面半径接触应力分布曲线

上一节分析的锥面密封是一种特殊的球面密封，锥面密封的弧面半径为无穷大，从上面分析的结果可以看出锥面密封的密封面接触应力峰值出现在密封面的两端，这与弧面半径不断增大应力峰值向密封面两端靠近的趋势相吻合。弧面半径较小时，因接触应力下降较快，应力值相差大，密封面接触应力分布不均；随着弧面半径增大，密封面的接触应力波动减小，弧面半径大的密封面比弧面半径小的密封面的接触应力分布更均匀。

3.3 螺纹牙受力分析

不同弧面半径的密封结构螺纹受力相似，为了分析螺纹牙的受力情况，本文以弧面半径为80 mm的球面密封结构为基础研究对象，分析了多组不同圈数螺纹的受力模型。图12是弧面半径80 mm模型的应力云图。图13、14分别是4圈螺纹和8圈螺纹应力云图。图15是不同圈数外螺纹各牙的平均应力曲线。从图15可以看出，前几扣螺纹的接触应力值较大，第一扣螺纹的应力值最大，随着螺纹牙序号的增加(螺纹牙序号排列如图13和图14所示)，螺纹牙的平均应力逐渐降低，但最后一扣螺纹牙的平均应力值出现了回升，整个螺纹牙面平均应力值曲线呈勾型，且螺纹圈数越多，曲线变化越平缓。对比不同圈数各螺纹牙的平均应力曲线可以看出，螺纹圈数多的曲线在螺纹圈数少的曲线之下，即螺纹圈数越多每扣螺纹牙的平均应力值越小，所承受载荷越少。螺纹圈数在4～10圈的各螺纹牙平均应力值曲线分布稀疏，螺纹圈数在10～16圈的各螺纹牙平均应力值曲线分布密集，这说明螺纹圈数少于10圈时，通过增加螺纹圈数能有效降低各扣螺纹牙的应力，减少每扣螺纹牙所受载荷，但当螺纹牙数超过10圈后，通过增加螺纹圈数来减少螺纹所受载荷的效果不是很明显，螺纹圈数设计为8～10圈较为合理。

图12 R=80 mm应力云图

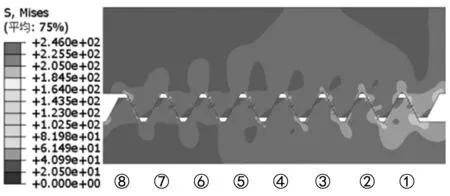
图14 8圈螺纹应力云图

图15 不同圈数外螺纹各牙平均应力曲线

从图15可以看出第一扣螺纹的受力最大，螺纹副的失效首先发生在第一扣上。为了研究第一扣螺纹牙的受力，本文在此分析了圈数为4、8和12圈外螺纹的第一扣牙面的应力分布情况，如图16所示。从16图可以看出，不同圈数螺纹第一扣螺纹牙的受力情况相似，曲线呈锯齿形，表明第一扣螺纹牙的受力不均匀。在螺纹牙的根部和顶部区域的应力较大，但根部区域附近的应力值更大且范围更广，最大应力值出现在内螺纹顶部与外螺纹牙面的接触处。螺纹圈数越多，第一扣螺纹的最大应力值越小，圈数从4圈增加到8圈时第一扣螺纹牙的最大应力值大幅度下降(M1→M2)，而圈数从8圈增加到12圈时最大应力值下降效果不是很明显(M2→M3)，再次证明螺纹圈数设计为8圈左右比较合理。

图16 外螺纹第一扣牙应力分布曲线

4 结 论

(1) 锥面密封结构接触应力峰值出现在密封面的两端位置，最大应力与最小应力相差大。锥面密封主要靠中间应力值较小但宽度较长的部分实现密封。在对锥面密封进行设计时应考虑到密封面两端的应力集中现象，设计出的锥面密封的密封性能更加可靠。

(2) 球面密封结构随着弧面半径的增大，接触应力值逐渐减小，密封宽度增大，但当弧面半径增大到一定值后，接触应力的减小幅度和密封宽度的增大幅度都趋于平缓。当弧面半径较小时，接触应力峰值出现在弧面和锥面的相切点，接触应力差值大；随着半径的增大，应力峰值向密封面两端靠近，密封面的应力波动减小，分布更均匀。在对球面密封结构进行设计时，应针对不同的工况，对弧面半径的选择既要考虑密封面的接触应力能封隔一定的压力差，也应考虑两密封面能有足够的密封宽度保证密封性能，以达到最佳的密封效果。

(3) 密封结构连接螺纹的前几扣螺纹牙受力较大，第一扣螺纹牙受力最大，随着螺纹牙序号的增加螺纹牙受力逐渐减小。螺纹圈数越多，螺纹承受载荷越少，但并不是螺纹圈数越多越好，随着螺纹圈数增多这种效应逐渐减弱。第一扣螺纹牙的最大应力出现在根部附近，在一定范围内增加螺纹圈数能有效减小第一扣螺纹最大应力值。螺纹圈数设计在8～10圈较为合理。

参考文献:

[1] 陆培文.阀门设计入门与精通[M].北京：机械工业出版社,2009.

[2] Phillips Dawnr R，Wingata Robert J.Seal Analysis for the Ares-I Upper Stage Fuel Tank Manhole Covers[R].USA: AIAA，2010.

[3] 张百麟.阀门泄漏的原因分析及其设计选型的优化[J].石油化工环境保护，2003，26(2): 58-61.

[4] 步玉环，孔 华，国安平，等.特殊螺纹接头主密封优化研究.润滑与密封，2011,36(4):15-20.

[5] 张建伟.ABAQUS 6.12有限元分析[M].北京：机械工业出版社，2014.

[6] 韩 冲，张 勇.导管连接件球头—锥面结构密封性能研究[J].润滑与密封，2012，37(10):105-111.

[7] 周 伟，靳 萍，常晓林，等.基于扩展Lagrange乘子的Clough接触面模型及应用[J].岩土力学，2008，29(1):68-74.

[8] Simo JC，Taylor R L.Quasi Incompressible Finite Elasticity in Principal Stretches:Continuum Basis and Numerical Algorithms[J].Computational Methods in Applied Mechanics and Engineering，1991(85):273-310.

[9] 陈 珏，胡 军，赵运磊.基于ABAQUS的摩擦对拉深模具的影响研究[J].机械设计与制造,2013,51(6):228-230.