基于并行蚁群算法的无人机协同任务/航迹规划应用研究
2018-05-10吴蕊
吴蕊
(中国电子科技集团公司第二十研究所,西安 710068)
0 引言
多无人机协同作战是未来战场使用的主要形式,例如广域搜索和摧毁,情报监视和侦察,压制敌防空火力等[1]。它包括任务分配和航迹规划两方面,其目的是在满足各项战术和技术指标的前提下,针对不同用户提出的多任务需求,确定出各无人机的目标任务执行序列,并寻找从当前位置到目标的可行飞行航迹,使得整个无人机编队的整体作战收益最大,代价最小[2]。
现阶段,针对任务分配问题,主要有A*算法、遗传算法和基于合同网的方法等[3-4]。针对航迹规划问题,目前的研究成果主要有基于图论的方法、进化算法和Hopfield网络算法等[5-8]。但是无人机协同执行任务的过程中,由于作战任务的复杂性,任务分配和航迹规划是不可分割的,多无人机之间往往同时存在多类协同约束关系,包括任务偏序关系、时间协同约束和空间协同约束[9-10],现有方法并未对此进行综合考虑,因此规划的结果并不能很好的反映多无人机协同作战需求。
针对无人机协同任务/航迹规划问题的特点,综合考虑多类复杂约束条件,本文采用混合蚁群算法求解,利用蚁群算法构造备选航迹集合,设计了一种基于整数编码的遗传算法求解方法,对无人机、目标、航迹采用整数编码、优化操作。文中将其应用于SEAD的单任务和多任务作战中,仿真结果显示采用 ACS-GA算法优化得到的方案组合能更好地、更快地找到全局最优解。
1 任务/航迹规划数学模型
1.1 问题描述
多机协同作战控制结构如图1所示,其中,最底层为无人机实体,它接收自主导航模块产生的对于给定目标给定任务的一系列导航点。在总体作战规划中,目标分配模块、航迹规划模块、多机协调模块一起完成任务分配和航迹生成。目标分配模块完成所有作战计划中的目标分配工作;航迹规划模块输出无人机到达各目标的航迹点、燃油代价估计和威胁代价估计;多机协调模块确保在同一任务中无人机同时到达指定目标的雷达探测区域。
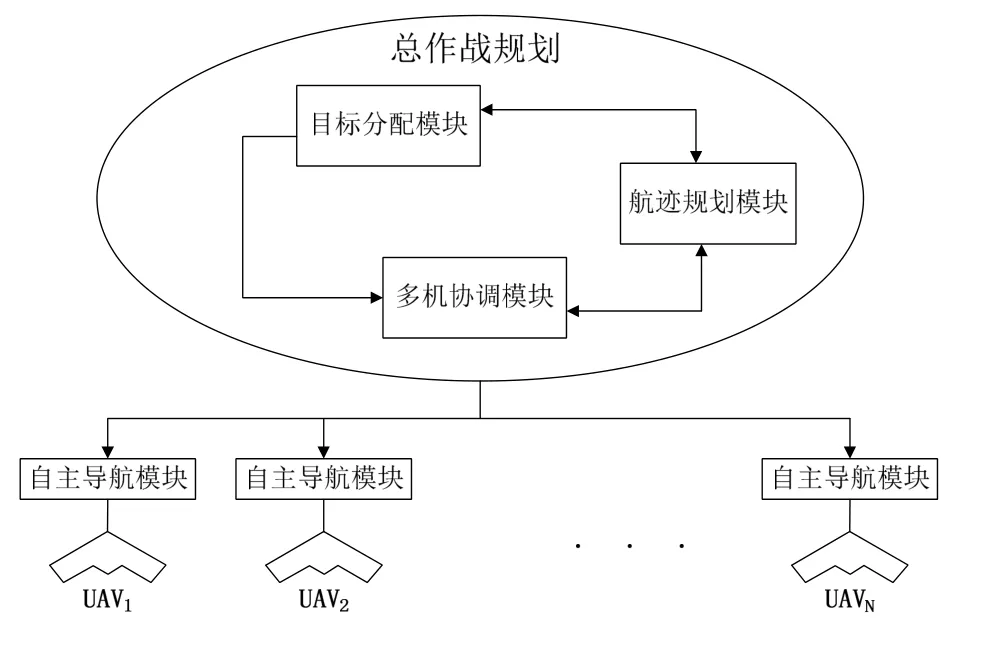
图1 无人机群协同作战控制结构
压制敌防空火力(Suppression of Enemy Air Defense,SEAD)任务是研究多UAV协同作战的典型模式,其中一个重要目标就是避开威胁到达指定的目标位置。因此该问题可由表示,其中E为基于Voronoi图的战场环境;V为由NV架UAV组成的飞机编队;为待执行的NT个目标集合;为各目标上需要完成的任务类型集合,一般包括m1=侦察(detection)、m2=攻击(destruction)和m3=毁伤评估(verification)三类;P为UAV的可选航迹集合;C为约束条件集合。
1.2 约束条件
(1)任务偏序关系
无人机群的一次作战任务,可以简述为,NV架无人机协同完成NT个作战目标上的M集合中的部分或全部任务类型。则作战目标ti中的mj任务表示为所需无人机架次表示为将每架次任务可以进一步表示为为了反映不同任务之间的偏序关系,为每个任务定义一个任务序号设置原则为:即

(2)时间协同约束
对于多无人机执行单一任务如同时攻击,时间约束是必要的。为此定义执行时间窗表示序号的任务的时间窗表示任务的起始时间表示任务的结束时间。则表示该任务的执行时间。当某任务需要多架无人机协同完成时,则多架次飞机的任务需要同时执行。即:当满足:

(3)空间协同约束
无人机攻击目的是扰乱敌方目标的防御系统,要求至少两架无人机同时集结目的地,以提高攻击毁伤率。当某任务需要多架无人机协同完成时,到达目的地时各无人机之间保持一定的夹角Ω。即:
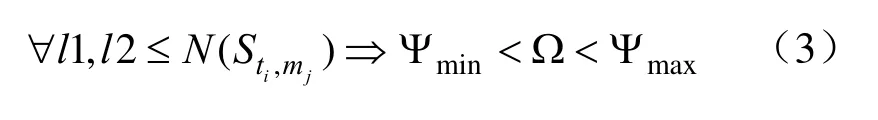
1.3 协同作战的评价指标
协同作战包括单机航迹代价评估和多机协同时间约束两方面,
(1)单机航迹综合代价评估

式中:lr,s是L(r,s)的航程,dr,k、ds,k、d1/2,k分别是第k个威胁距该航迹端点r、s和1/2处的距离。

其中,系数k表示威胁代价的权重,它反映了航迹规划时决策人的倾向性选择。
(2)协同时间代价评估
评估多机单次作战任务:首先计算单架次无人机到达目标的时间TOTk,i
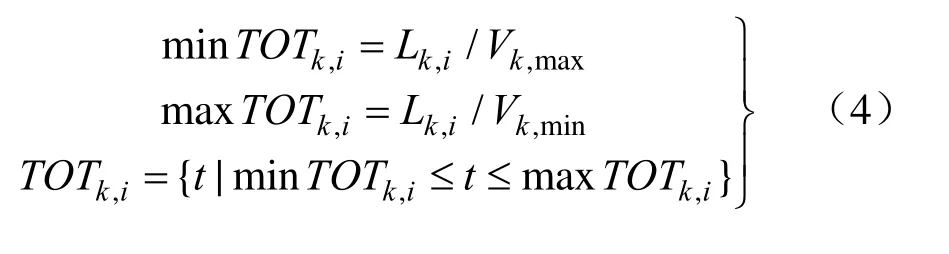
式中,Lk,i,Vk,max和Vk,min分别表示第k架无人机到达目标Ti的航程、最大速度和最小速度。则TOTi为到达目标Ti的ni架无人机的时间的交集:

评估多机连续作战任务:定义为同一目标的任务mn-1和任务mn的时间间隔。根据任务的偏序关系,从起始时刻到依次完成m1、m2、m3任务的结束时刻,存在以下关系:

因此综合代价可以表示为:

其中f1为多机协同性能评估,衡量多机协同任务时间代价,并以协同变量作为每架无人机之间交流的内容;f2为单机航迹综合代价评估,直接衡量了各个无人机航迹综合代价之和,多 UAV协同作战的评价目标是同时最小化f1和f2。
2 并行蚁群算法的任务/航迹规划
2.1 并行蚁群的建立
根据上一节所讨论的问题模型,本文设计一种并行多子群蚁群算法。根据任务计划将不同的任务映射为人工蚁群中的不同蚂蚁子群,各子群搜索寻找执行某一任务的无人机组及其飞行航迹。设人工蚁群为其中为对应的第i次任务的蚂蚁子群,且不同子群间满足式(10)

式中,Anti,j为第i个子群中第j个人工蚂蚁,蚂蚁子群ACi中每个蚂蚁构造执行目标i上的任务的无人机组及其对应飞行航迹,因此所有目标的任务集合需要来自不同蚂蚁子群的NT×M个人工蚂蚁构造的无人机组序列。构造一个满足各类约束条件的任务/航迹分配方案的NT×M个人工蚂蚁,称为人工蚂蚁簇AGi是人工蚁群中构造一个完整的分配方案的最小蚂蚁群落,且不同的人工蚂蚁簇之间满足:

2.2 任务分配方案的构造
构造方案的基本群落是人工蚂蚁簇。人工蚂蚁簇AGi中的每一个人工蚂蚁依次为对应的任务构造无人机组合。每个人工蚂蚁根据状态转移规则在候选集合中选择无人机组。
2.3 蚂蚁子群的状态转移规则

每个子群建立启发因子矩阵,根据综合代价建立启发因子矩阵。
3 仿真实验及结果
假设NV=6,NE=50,NT=3,威胁代价的权重k=0.5,无人机飞行速度取值范围为[4,6],蚂蚁数m=30,ρ=0.3,Q=2,α=1,β=1,限定蚂蚁寻径循环次数 NC_max=100,遗传迭代次数 Generation=500,交叉因子PC=0.9,变异因子Pm=0.2。
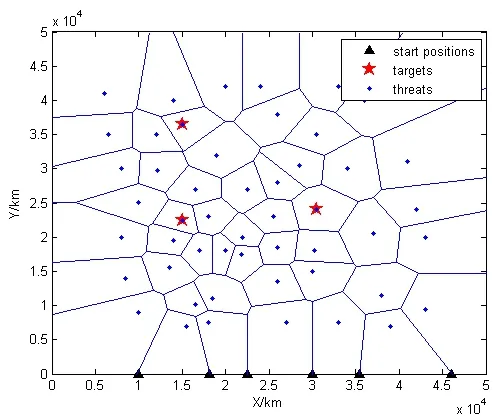
图2 SEAD任务模型
对于单任务作战的任务/航迹规划问题,采用本文中的混合算法,最终任务分配方案如表 1所示,6架UAV两两编队同时到达各目的地。

表1 单任务作战的分配方案


图3 单任务仿真结果
图 3(a)~(c)分别是各目标的任务分配和航迹规划结果,可以看出,采用混合算法所得结果可以满足无人机协同的诸多约束条件,满足协同任务的需求。图4为采用该方案所得无人机到达目标的距离时间曲线,不同无人机同时到达同一目标执行任务。由于该方案是多次执行500次迭代所得,因此协同时间*
TOT最小。图 5表示该任务的收敛曲线,随着算法的迭代,各目标任务逐渐收敛得到最小代价值,总任务的平均代价也逐渐趋于稳定,图中所示的实验在算法迭代 36次后,总协同代价达到收敛时的水平。
4 结论
本文所述利用混合 ACS-GA算法在解决无人机协同任务/航迹规划问题时,发挥了各自的优点。仿真结果表明,利用蚁群算法求得的航迹能够回避各种威胁,并构造出初始解空间;利用遗传算法对无人机、目标、航迹编码设计,并能够在较少的迭代次数内获得较优的作战方案。

图4 无人机到达目标的距离随时间变化曲线

图5 综合协同评价指标收敛曲线
参考文献:
[1]Eun Y, Bang H.Cooperative Task Assignment/Path Planning of Multiple Unmanned Aerial Vehicles Using Genetic Algorithms [J].Journal of Aircraft, 2009,46(1):338-343.
[2]Barabto G.Uninhabited combat air vehicle controls and displays for suppression of enemy air defenses [J].CSER IAC Gateway, 2000, 11(1):1-4.
[3]Atkinson M L.Contract nets for controls of distributed agents in unmanned air vehicles[R].AIAA-2003-6532,2003.
[4]MacKenzie D C.Collaborative tasking of tightly constrained multi-robot missions[C].Proceedings of the Second International Workshop on Multi-Robot Systems.2003:39-50.
[5]McLain T,Beard R.Trajectory Planning for Coordinated Rendezous of Unmanned Air Vehicles[J].AIAA Guidance, Navigation and Control,2000:2000-4369.


