一种攻击角可控的无人机滑模导引律

王雅君

（中国电子科技集团公司第二十研究所 西安 710068）

0 引言

无人机导引律是描述攻击型无人机在拦截目标时应遵循的质心运动规律。要对大机动目标实施成功拦截，除了需要提高无人机自身的机动能力，也对导引律提出了更高的要求。

Brierley和Longchamp[1]在1990年时最先将变结构控制的思想引入空-空导弹制导律的设计中，所得的制导律对于运动模型的不确定性、目标机动等具有较强鲁棒性。周荻等人[2-3]针对线性时变系统设计了一种自适应滑模趋近律，据此设计的制导律有较高的命中精度。作者还将很难精确测得的目标机动加速度视为外界干扰，并证明了在干扰项有界的条件下，自适应滑模制导律对外界干扰和自身的参数摄动有不变性。徐世许和马建敏[4]引入了终端滑模面，即在滑模面中加入非线性项，既能保证系统轨迹较快地到达滑模面，又能使滑动模态以较快的速度收敛到平衡点。

滑模变结构导引律的设计中，切换面的选择至关重要。线性切换面只能保证系统状态渐进收敛，而无法在有限时间内使其严格收敛到零。为此，本文采用终端滑模面来设计控制律，即通过在切换面方程中引入非线性项，在保证控制系统稳定的基础上，实现系统状态在有限时间内对期望值的完全跟踪。

1 运动模型的建立

图 1所示为纵向平面内的无人机-目标相对运动关系，模型建立在极坐标系中，将无人机和目标都视为质点，不考虑其姿态控制问题，也不考虑自动驾驶仪的动态延迟问题。

图1 二维无人机-目标相对运动关系

图1中，无人机和目标分别位于M和T处，它们之间的距离为r，二者连线MT就是视线（LOS，Line of sight），视线与参考方向的夹角q即为视线角，也叫做攻击角。θm和θt分别是无人机和目标的速度矢量与视线的夹角，即前置角。

根据图1中的几何关系，可以建立如下的相对运动方程组：

对式（1）中的两式分别求导，并令

可以看出，分别为无人机和目标的机动加速度在视线法向的分量。uq即为无人机控制律，是施加在无人机上的指令加速度。而由于目标机动通常无法精确获知，因此在实际设计过程中常将ωq作为一个有界的外部干扰来考虑。

对式（1）求导并将式（2）代入，化简可得用视线角速度表示的相对运动方程

2 非线性系统的有限时间稳定

系统的有限时间收敛指的是系统状态能够在有限时间内到达平衡点，使系统在有限时间内稳定。设非线性系统有一个位于原点的 Lyapunov意义下稳定的平衡点，即

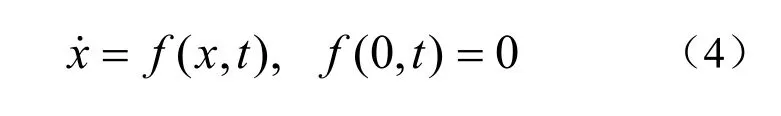
引理1[6]对于式（4）表示的非线性控制系统，若存在定义于的邻域上的光滑函数V（x），并且存在实数使得上正定，且在上半负定，则以式（9）表示的系统在x=0处有限时间稳定，系统的停息时间与初始状态x0有关，有

其中，若则该系统在x=0处全局有限时间稳定。

3 非奇异快速终端滑模算法

快速终端滑模可以由以下的一阶微分方程表示：

其中，α＞0，β＞0，0＜γ＜1。可以看出，当系统状态远离平衡点时，αx起主要作用，使状态轨迹快速向平衡点运动；而当系统状态运动到平衡点附近时，起主要作用的一项变为系统状态依然能够快速收敛。因此，快速终端滑模可以使系统状态在整个运动过程中都保持较高的收敛速度，从而确保了系统优良的动态性能。

下面分析快速终端滑模的有限时间收敛性。对于式（5），选取 Lyapunov函数对其求导，并将式（5）代入，有

即是半负定的。令引理1中的常数则状态轨迹从任意初始状态出发，收敛至平衡点所需的时间满足

其中，x0为系统的任意初始状态。

形如式（5）的快速终端滑模虽然能够迅速收敛，但会产生奇异问题，这是由于终端滑模函数中的非线性项在求一阶导后产生了负指数项，因此，可以通过合理选择非线性项来避免奇异问题。非奇异的快速终端滑模函数表达式如下所示：

式中，

文献 7详细地给出了式（8）所示系统的有限时间收敛性证明，但收敛用时的表达式和证明过程过于复杂，不便于实用，在后文中用到相关结论时，会根据具体的导引律，推导出更为简便的表达形式，因此将其证明过程略去。

4 攻击角可控导引律设计

将前文建立的相对运动模型式（3）结合图 1中的相对运动关系，可知无人机的指令加速度是施加在速度法向上的，因此控制量前需要加上一个方向余弦系数，式（3）变为

用qd来表示期望的攻击角（qd为一定值），选择视线角与期望攻击角之间的偏差和视线角速率作为系统状态变量，即令可得

需要特别指出的是，快速终端滑模算法也可以用作趋近律设计。由于奇异问题是由指数函数求导产生的负指数项导致的，而式（5）不含有负指数项，因此不会产生奇异问题。

根据非奇异快速终端滑模算法式（8），设计滑模切换面如下：

其中该切换面具有与式（5）完全相同的形式，因此是全局快速收敛的，并且能够避免产生奇异问题。

根据快速终端滑模算法式（6），设计趋近律如下：

其中，α＞0，β＞0，0＜γ＜1。根据式（11）及式（12），有ss’≤ 0，因此滑模切换面满足到达条件，系统状态轨迹能够在有限时间内到达切换面。

对式（11）求导并与式（12）联立，将式（10）代入，ωq视为干扰项，可以解出控制律

即为带攻击角约束的有限时间收敛非奇异快速终端滑模导引律。

5 有限时间收敛性分析

滑模控制系统的状态变量要经历两个运动阶段：趋近运动阶段和滑模运动阶段。下面首先分析趋近运动阶段的收敛特性。

选取 Lyapunov函数为V=s2，求导，并将导引律u代入其中，得到

至此，将按照目标是否机动（即ωq项是否为零），分两种情况分别加以讨论。

（1）目标不机动，对应于即目标静止或进行匀速直线运动：

此时直接应用引理 1，令其中c=2β，则状态轨迹从任意初始状态出发，运动到切换面所需的时间满足

（2）目标机动，即

此时，式（14）可以改写成以下形式：

在x2≠0时，只要调节趋近律参数，保证s 2的系数为负，那么式（16）与情况（1）具有相同的形式，从而保证其有限时间收敛的性质，直到s 2的系数变为正。若以f表示目标机动加速度ωq的上界，则系统状态轨迹能够在有限时间内运动到切换面s=0两侧的小区域内：

对于x2=0的情况，由于系统此时尚处于到达运动阶段，因此系统状态不可能位于区域|s|≤Δ内，因此有x˙2≠0，这说明x2=0不是系统在到达运动阶段的吸引子。综上，在目标进行机动时，系统状态能够在有限时间内运动到区域|s|≤Δ以内。

通过以上的分析可知，滑模导引律式（13）满足切换面的到达条件，不论目标是否机动，制导系统状态变量均能够在有限时间以内从任意初始状态运动到切换面或其小领域内。下面分析第二阶段——滑模运动阶段的收敛情况。

系统状态进入区域|s|≤Δ后，系统开始滑动模态运动，此时假设s=τ，其中|τ|≤Δ。将其代入切换面式（11），可改写为以下形式：

它与切换面式（12）具有相同的结构，这说明系统状态轨迹将一直收敛，直到条件不再满足，因此x2能在有限时间内收敛到区域同理，视线角偏差x1能够在有限时间内收敛到区域

综上所述，以式（13）所示的形式设计导引律，能够保证：对于匀速直线运动或静止目标，制导系统状态变量能够在有限时间内运动到切换面上，进入切换面后，视线角偏差θ和视线角速度也能够在有限时间内收敛到零，全程不会发生奇异问题；

对机动目标，制导系统状态变量能够在有限时间内运动到切换面的邻域|s|≤Δ内，进入切换面后，θ和也能够在有限时间内分别收敛到区域|s| ≤|Δθ|和|s| ≤ |Δq|内，全程不会发生奇异问题。

6 仿真分析

将式（13）所示的导引律记为 NFSMG，本节将其与普通的滑模制导律（记为SMG1）分别仿真并对比试验结果。后者采用线性滑模面及自适应趋近律。仿真的初始条件如下：

（1）无人机初始位置为（0km，0km），初始航向角 90°，飞行速度 800m/s；目标初始位置为（12km，5km），初始航向角 120°，飞行速度 500m/s；

（2）NFSMG 仿真参数：k1= 1，k2= 2，a1= 2，a2= 1.5，α= 750，β= 750，γ= 0.5；

（3）目标进行正弦机动，机动加速度为对于无人机的制导系统，目标的机动情况是未知的，将其视作外界扰动。

两种导引律对机动目标的拦截情况如图2所示。

表1中列出了目标进行未知机动时两种导引律在不同期望攻击角下的脱靶量和拦截用时。

表1 目标机动时不同期望攻击角下的脱靶量和拦截用时比较

可以看出，NFSMG的脱靶量和拦截时间都明显小于SMG1，说明在对机动目标的拦截上，本文提出的NFSMG相较于传统的滑模制导律，具有更高的命中精度、更短的打击时间和更少的燃料消耗。这一优势也能从拦截轨迹上直观地体现出来。

图3所示为30°期望攻击角下两种导引律需用过载的变化情况对比。

图3 需用过载的变化情况

从图3中可以看出，NFSMG的需用过载在开始时刻和命中点附近出现了峰值，达到了可用过载的极限，这是由于在这两个区间无人机导引律需要进行大幅度的转向。而SMG1的需用过载曲线不仅在大部分时间都达到了可用过载的最大值，而且有很多个突变点，这说明指令加速度的方向在频繁地改变。因此NFSMG在末制导阶段所需的燃料量远小于SMG1的量。

从以上两个场景的仿真中可以看出，本章提出的NFSMG导引律在拦截用时、命中精度、收敛速度、燃料消耗等各项指标上，都拥有优良的性能，尤其在对机动目标的拦截方面，优势更加突出。

7 总结

本文应用快速终端滑模算法，设计了一种能够快速收敛且不会发生奇异问题的滑模制导律，在拦截机动目标时视线角偏差和视线角速率都能够在有限时间内收敛到零附近的小邻域。仿真结果说明该导引律拥有优越的动态性能，满足攻击角约束的条件，并且航迹平直，能量消耗较少。后续的研究可以考虑对无人机自动驾驶仪的动态延迟进行补偿，并将质点导引律扩展到三维空间。

参考文献：

[1]S D Brierley, R Longchamp.Application of sliding mode control to air-air interception problem[J].IEEE Transactions on Aerospace and Electronic Systems, 1990,26（2）: 306-325.

[2]周荻, 慕春棣, 徐文立.空间拦截智能自适应变结构导引规律研究[J].宇航学报, 1999, 20（3）: 60-65.

[3]徐世许, 马建敏.不确定多变量线性系统的快速收敛滑模控制[J].系统工程与电子技术, 2011, 33（7）:1585-1589,1672.

[4]方勇纯, 卢桂章.非线性系统理论[M].北京: 清华大学出版社, 2009.

[5]Bhat S P, Bernstein D S, Finite-time stability of homogeneous systems[C].Proceedings of American Control Conference, Albuguerque, New Mexico, 1997,2516-2514.

[6]Liang Y, Yang J Y.Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control, 2011, 21（6）:1865-1879.