粗心的毛毛熊
2018-05-10
在认识三角形和四边形时,毛毛熊出了不少错误,可他不知道错在哪里。小朋友,让我们一同来帮帮他吧!
[病例1]一个三角形每个内角的度数都不小于60°,这个三角形是( )三角形。
[病症]不能确定是什么三角形。
[诊断]因为三角形的内角和是180°,并且它的每个内角的度数都不小于60°,所以它的每个内角只能都是180°÷3=60°,也就是这个三角形是等边三角形。
[处方]这个三角形是等边三角形。

[病例2]已知一个等腰三角形两个内角的和是70°。求底角的度数。
[病症]底角的度数是180°- 70°=110°。
[诊断]如果这个三角形一个底角的度数是110°,那么这个三角形两个底角的度数之和是110°×2=220°,这与三角形的内角和是180°相互矛盾。因此,题中“70°”不可能是等腰三角形一个底角与一个顶角的度数和,只能是等腰三角形两个底角的度数和。
[处方]每个底角的度数是70°÷2=35°。
[病例3]一个三角形被纸片遮住了一个角,露在外面的角是两个锐角。你知道这是一个什么三角形吗?
[病症]这是一个锐角三角形。
[诊断]每个三角形都至少有两个锐角,但题中只说露在外面的是两个锐角,我们并不能测算出这两个锐角的和是多少度,这样也就不能推算出遮住的角是多少度。因为不知道遮住的角是个什么角,所以我们不能确定这是个锐角三角形。如果露在外面的两个锐角的和大于90°,那么这个三角形就是锐角三角形;如果露在外面的两个锐角的和等于90°,那么这个三角形就是直角三角形;如果露在外面的两个锐角的和小于90°,那么这个三角形就是钝角三角形。
[处方]这个三角形可能是锐角三角形,也有可能是直角三角形,还有可能是钝角三有形。
[病例4]小虎说:“直角三角形中两个锐角的和一定小于钝角三角形中两个锐角的和。”他说得对吗?
[病症]对。
[诊断]毛毛熊忽视了三角形的内角和与其中两个锐角的关系。因为三角形的内角和是180°,所以直角三角形中两个锐角的和为180°-90°=90°。而钝角三角形中两个锐角的和=180°-钝角的度数,又因为钝角的度数大于90°,所以钝角三角形中两个锐角的和小于90°,即比直角三角形中两个锐角的和小。
[处方]错。
[病例5]一个等腰三角形两条边的长度分别是5厘米、10厘米,那么这个等腰三角形的周长是多少厘米?
[病症]这个等腰三角形的周长是5+5+10=20(厘米)。
[诊断]毛毛熊错在认为等腰三角形的腰长是5厘米。因为两条腰的长度和与底边的长度都是10厘米,这与“三角形任意两边之和大于第三边”相互矛盾,所以这个等腰三角形的腰长只能是10厘米,底边的长度是5厘米。
[处方]这个等腰三角形的周长是10+10+5=25(厘米)。
[病例6]小虎说:“有一组对边平行的四边形一定是梯形。”他说得对吗?
[病症]对。
[诊断]梯形是只有一组对边平行的四边形,“只有一组”的意思是另一组不能平行。“病例”中“有一组对边平行的四边形”并没有说明另一组对边是否平行,这样另一组对边可能不平行,也可能平行。因此,有一组对边平行的四边形可能是梯形,也可能是平行四边形。
[处方]不对。
[病例7]数一数,下图中有几个平行四边形和几个梯形?
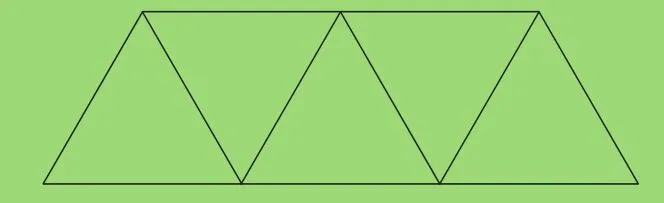
[病症]有4个平行四边形,2个梯形。
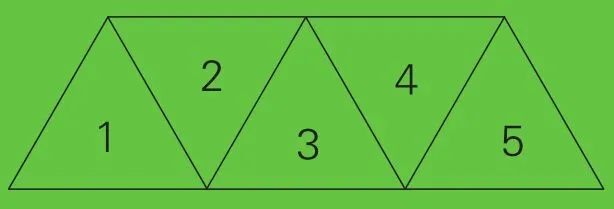
[诊断]毛毛熊数时出现了遗漏。要不重不漏地数出图中所有的平行四边形和梯形,可以先给图中每个小三角形标上序号(如右图),再将它们由少到多地进行组合。由2个三角形组成的平行四边形有12、23、34、45共4个,由4个三角形组成的平行四边形有1234、2345共2个,所以平行四边形共有4+2=6(个);由3个三角形组成的梯形有123、234、345共3个,由5个三角形组成的梯形有一个,所以梯形共有3+1=4(个)。
[处方]平行四边形有6个,梯形有4个。
