基于改进Leaders算子的审计潜在疑点发现

邵锦炜,林 俊,刘雅婷,肖嘉丽

(1.广东电网有限责任公司云浮供电局,广东 云浮 527300; 2.广东电网有限责任公司信息中心,广东 广州 510620; 3.广东电网有限责任公司揭阳供电局,广东 揭阳 522000; 4.广东电网有限责任公司,广东 广州 510620)

0 引 言

随着企业业务数据量的增大，被审计单位的审计数据呈海量化的增长趋势，已建立起TB甚至PB级的大数据库[1]。面对海量审计数据，如何整合并充分利用这些数据，实现审计大数据的全覆盖并从中发现疑点，是计算机审计面临的迫切要求和全新挑战。

目前计算机辅助审计主要采用审计数据库语句查询方法，该方法对审计人员的已有知识要求较高，需要审计人员对业务逻辑关系、数据勾稽关系等具有丰富的审计经验，但往往审计人员经验水平不一，当面对大型央企成百上千、行业千差万别的下级公司和关联公司时，巨大的数据量仅靠先验知识难以面面俱到，此时经验式的语句查询并不能充分发挥大数据在揭示数据疑点方面的优势。另外，审计经验往往落后于审计数据的发展，使得许多新的审计疑点不能被及时发现，给审计带来风险。

数据挖掘[2]可以从大量不完全且随机的数据中，提取潜在的有用信息。而聚类作为无监督的数据挖掘方法，在无先验知识的前提下揭示数据之间的内在关系[3]，应用于审计业务时，在选择恰当的审计指标基础上，可以从海量数据中将具有审计疑点的少量数据进行聚类，从而配合审计人员审计经验快速精确定位审计疑点，既充分利用大数据优势又能揭示潜在的新的审计疑点。

目前，数据聚类技术在审计领域已有较多研究，王会金[4]采用数据挖掘技术构建了计算机辅助审计的框架；秦志光等人[5]分析大数据环境云存储技术的数据完整性，提出了基于云存储技术的大数据审计；秦荣生[6]探讨了大数据云计算技术对于审计大数据的影响；程平等人[7]引入了COBIT实施的促成因素，构建了大数据审计环境下基于云会计的“互联网+审计”模式。但这些研究大多停留在理论探讨阶段，较少涉及大数据审计实施问题。

针对大数据聚类，CLARANS算法[8]、CURE[9]算法通过随机抽样和样本集划分，消除异常点，完成大数据集聚类，但其收缩因子预设对算法效果影响较大；Vijaya等人[10]提出Leaders-subleaders层次聚类算法，基于Leaders算子，迭代计算subleader，提高了算法的聚类精度。Viswanath等人[11]提出了针对大数据的Rough-DBSCAN算法，利用Leaders算法进行初始聚类，然后针对获得的代表点集，应用DBSCAN算法进行再次聚类。

本文在已有研究基础上，提出将改进Leaders算子的迭代式聚类方法用于发现审计大数据疑点，算法采用Leaders算法完成审计大数据的自动初始聚类，并通过随机抽样融合对初始聚类结果优化，最后通过迭代聚类方法，对实例数较少或可疑程度易被掩盖的小簇进一步聚类，实现审计大数据的精确聚类，并将实例较少的异常簇识别为潜在疑点，实验验证了算法在审计大数据疑点发现的有效性。

1 抽样融合改进Leaders算子

聚类能够在无先验知识下，将具有共同特征属性的数据聚成一个簇，而审计聚类中包含较少实例的簇，简称为“小簇”[12]，由于其与实例较多的“大簇”之间的检测特征属性差异较大，因此可被视为潜在的审计疑点。但在一组待审计大数据中，潜在的疑点簇和不相关小簇并不能依靠审计经验确定聚类中心数。为此，本文采用Leaders算法对审计大数据进行自动聚类，获取初始聚类中心，然后通过抽样融合方法对初始聚类中心进行优化，从而精确确定潜在的疑点簇及不相关的小簇的聚类中心，为审计人员提供疑点发现指导。

1.1 Leaders算法审计大数据自动聚类

基于增量聚类的Leaders算法[13-14]能够忽略聚类类别的归属模糊性，不需指定聚类中心数，仅扫描一遍数据并选取簇的leader代表点实现聚类，且仅存储提取的leader，节省运行时间和存储空间，对处理大规模数据十分有利[15]，其算法流程如算法1所示。

算法1Leaders算法

算法描述：根据Leaders算法对大规模数据进行聚类

Input：数据集X和距离阈值T

Initialization：

1.存放数据集leader的数组L初始化为空集Φ；

2.数据集含有的leader数l初始化为0;

Iteration:

3.for每一个数据点xido

4.for leader∈L且‖leader-xi‖≤T do

5.if (没有满足条件的leader或 L=Φ) then

6.L=L∪{xi};l=l+1;

7.else

8.将xi归类为当前leader代表类别中；

9.end if

10.end for

11.end for

Output:leader的集合L;leader的个数l;聚类结果

如图1所示，Leaders算子能够自动计算审计数据的聚类中心，但其对数据点的输入顺序敏感，易出现类内相似性大于类间相似性情况，加之固定距离阈值的聚类方式，使得结果分布较为均匀，因此Leaders算子尽管可以得到审计数据的初始聚类中心，但聚类结果不能令人满意。

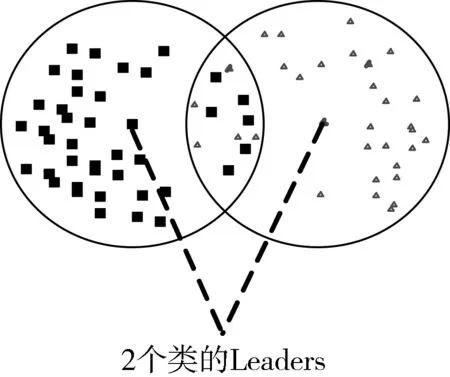
图1 Leaders算法中不好的聚类结果

为此，结合已有研究成果，本文以Leaders算法聚类中心为初始值，结合k-means算法，通过随机抽样融合方式对结果进行优化，以期精确聚类审计疑点簇及不相关的小簇。

1.2 抽样融合改进Leaders算法

以Leaders算法获得的聚类中心作为初始值，进行多样本集随机抽样和样本集内k-means[16]聚类，并对聚类后的样本并集重新聚类，得到最终原始数据的聚类中心，既克服了Leaders算法的不足，又充分利用了k-means算法的优势，获得较好的聚类效果。

1.2.1 数据抽样

数据抽样在降低数据量提高处理速度的同时将图1交集部分数据分散到小样本集中，从而在小样本集内重新进行聚类判断。小样本集以每个初始聚类中心进行随机抽样，其数据规模按文献[15]方法计算：

(1)

式(1)中，f是抽取比例，n为审计数据量，ni为簇Ci数据量。式(1)表示以概率1-δ(0≤δ≤1)抽取至少f×ni个数据大小的样本s，其计算的数据规模仅占原始数据较少的比例[15]。

最理想的抽样应覆盖原始审计大数据的所有类别，但为控制样本集数据量以发挥k-means算法优势，单个样本集聚类中心会偏离原始大数据聚类中心，且聚类中心也不能很好地覆盖所有原大数据集的所有类别，为此，本文对每个Leaders初始聚类中心进行多次随机抽样，一方面大数据初始簇中由于Leaders算法不精确导致的不同类别数据，经多次随机抽样后，可以等概率地进入样本集中，从而形成新的聚类中心，另一方面，图1交集数据经随机抽样后，也会等概率地进入样本集中，通过重新聚类而明确这些数据的类别，因此，对Leaders初始聚类中心进行多次随机抽样，可以使初始聚类错误的数据以及图1中的交叉数据等概率地进入样本集而重新聚类，以使抽样样本集的并集可以最大程度地覆盖原始大数据的所有类别。在此基础上采用如图2所示的多样本集聚类中心融合的方法计算样本集并集的聚类中心，从而最大程度地还原原始审计大数据的聚类中心。对Leaders初始聚类中心进行多次随机抽样，既保证k-means算法所需的样本规模足够小，又保证了抽样样本并集对原始大数据自然簇的理想覆盖。

1.2.2 样本集并集聚类中心的确定

如图2所示，根据式(1)计算的样本集规模，对Leaders初始聚类中心进行多次随机抽样，形成数据规模较少的多个样本集，然后对每个样本集进行经典的k-means算法聚类，其中k的初始值设为Leaders算法初始聚类中心数，以解决k-means算法迭代次数依赖于初始聚类中心的NP难题，同时，由于单样本集聚类过程都是独立进行，可以采用并行处理加速样本集聚类。

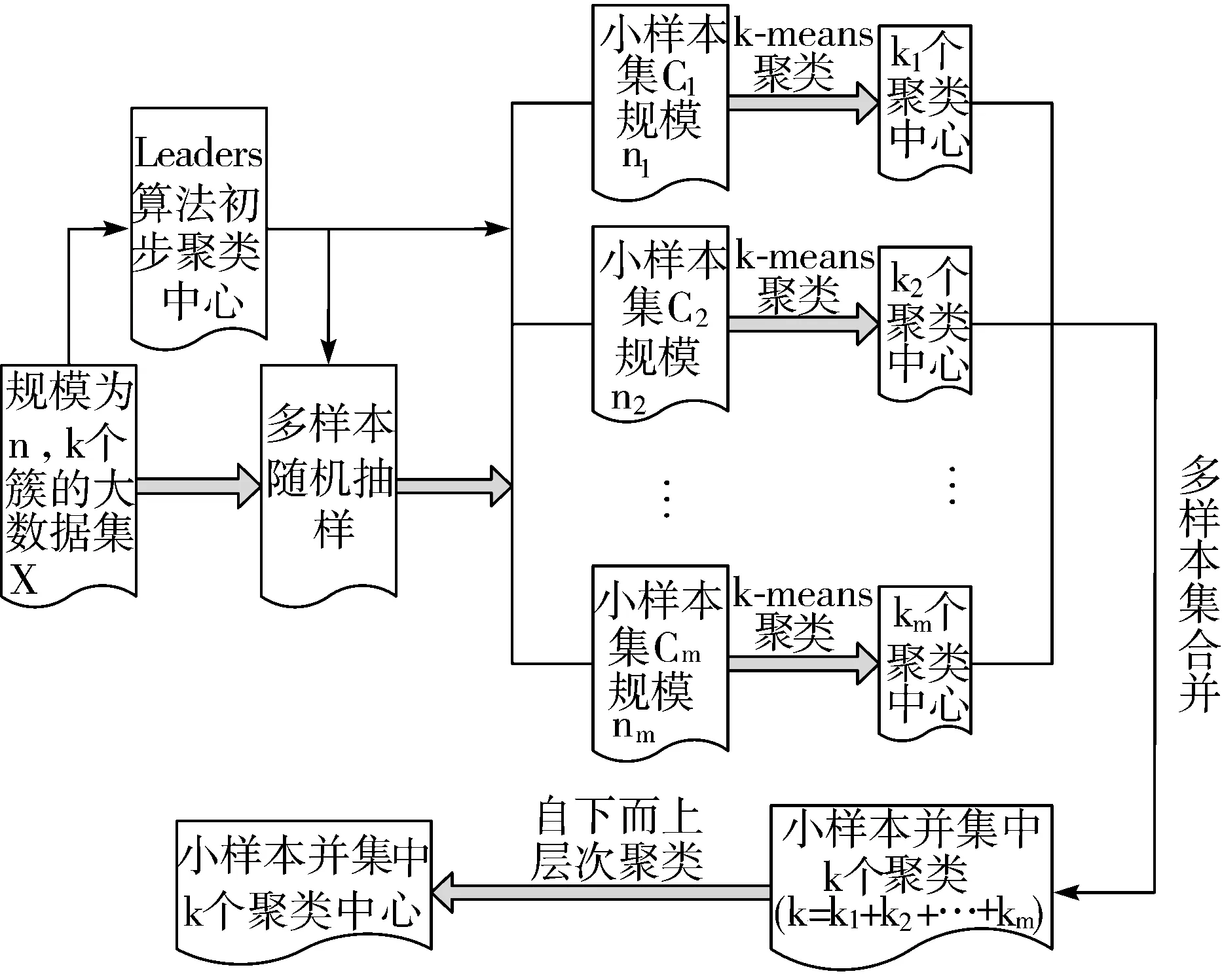
图2 多样本集聚类中心融合过程改进Leaders算法

设所有样本集进行聚类后，第i个单样本集覆盖类别为ki(1≤ki≤k)，将所有样本集合并得到k(k=k1+k2+…+km)个聚类簇，计算每个簇的均值：

(2)

其中，xi为簇Ci的均值，ni为其数据量，xij为某个数据属性。采用自下而上的层次聚类方法，计算每2个簇之间的均值距离：

dis=|xi-xj|2

(3)

当小于预设的阈值T时，则合并2个簇，并重新计算其均值，对样本并集所有聚类中心融合聚类后，最大程度地得到原始数据的聚类中心数及初始位置。

对抽样剩余的数据，按式(4)规则进行聚类，以此完成所有数据的重新精确聚类。

(4)

其中，xi为融合聚类中心位置，xΔ为抽样剩余数据。

2 基于改进Leaders算子的审计疑点发现

在选取审计关注点，整理数据后，首先通过Leaders算法获取数据的初始聚类中心，然后采用随机抽样融合和k-means方法对初始聚类进行优化，从而最大程度地获得原始审计大数据的精确聚类，将聚类中实例数占比小于10%的簇视为审计疑点小簇，辅助审计人员进行准确疑点判断。

但由于等概率随机抽样融合容易对过小小簇抽样数据较少而无法在样本集中形成聚类中心，或可疑程度较低的疑点通常会被可疑程度更高的疑点所掩盖，从而使得采用改进Leaders算法聚类后，仍会存在可疑小簇不能被准确聚类，如图3所示，图中*、△和×表示数据实例，同圆中的实例为一个簇，由图可见，虚线圆外的小簇中的实例与其他多数实例差异较大，可被视为审计疑点，但虚线圆内中除去实线圆内数据为一类外，还存在未被准确聚类的小簇，如果仅采用一次聚类，则不能筛除这些疑点小簇。为此，在进行一次聚类筛除疑点小簇后，将数据实例较多的大簇重复迭代进行聚类，直到达到满足要求的小簇数或迭代次数为止。重复聚类过程中，对于数据实例巨大的簇，采用改进Leaders算法进行聚类，而对于数据量不大的簇，可以直接采用k-means等聚类方法。

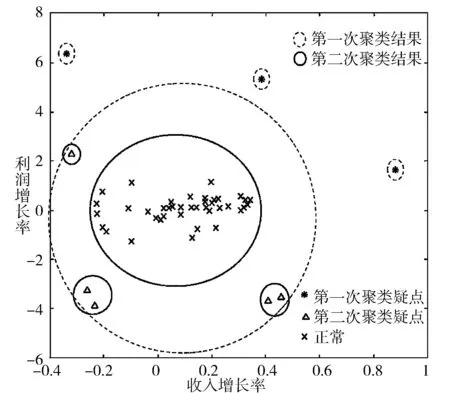
图3 二维特征实例的聚类过程与结果

3 实验验证

实验采用仿真数据集和真实数据集来测试本文算法对审计疑点发现性能，仿真数据采用IBM数据生成器[17]生成，并与已有方法进行性能比较，真实数据集为网上的公开数据，通过证监会等机构公开的处罚信息进行验证。

3.1 人工生成数据集实验分析

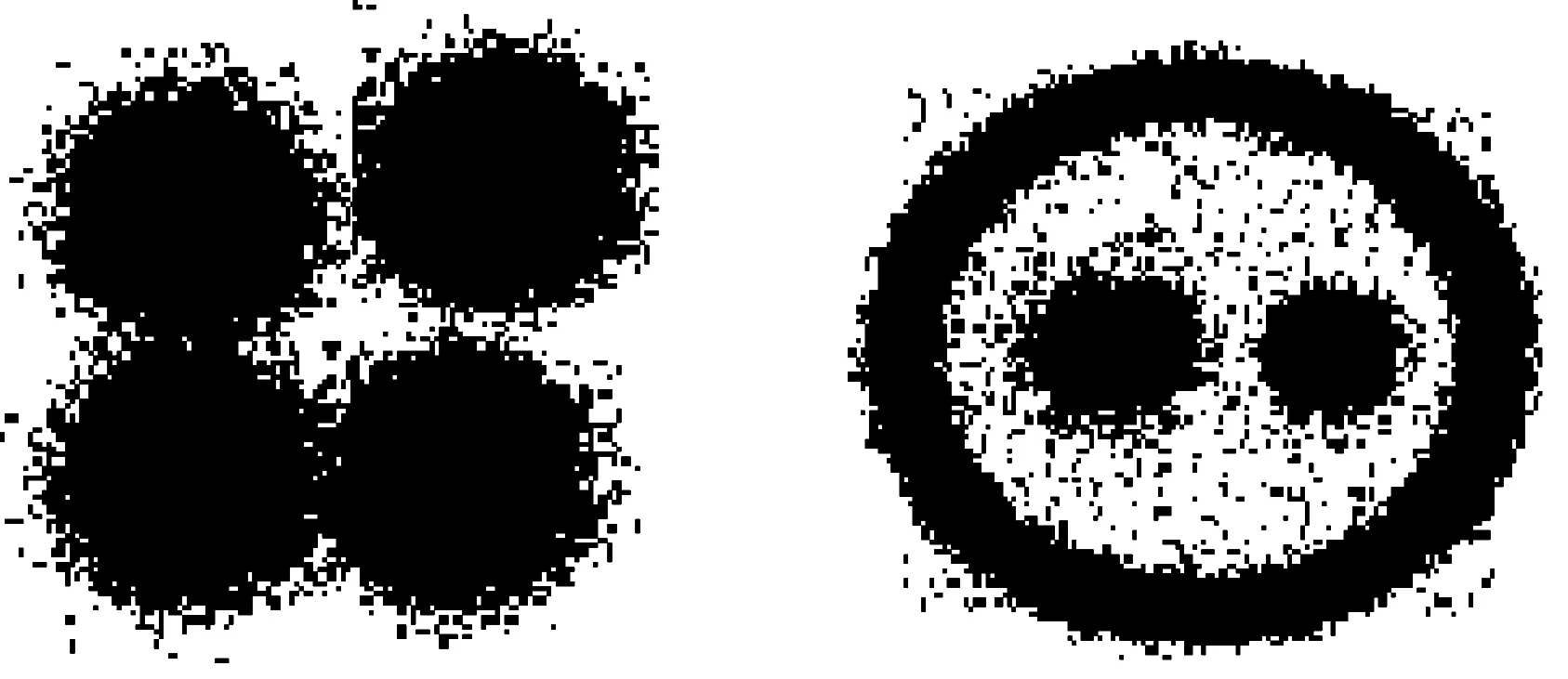
(a) 数据集1 (b) 数据集2图4 仿真数据集几何形状

如图4所示，实验选用二维空间上2个人工数据集，表1给出了数据集的基本信息并增加不同数量的随机噪声点，实验运行在Intel(R) Core(TM) i5-2540M-CPU@2.60 GHz，4 GB的计算机上。

表1 仿真数据集基本信息

数据集数据量噪声数数据集形状簇数据集11500001500同规模的圆4数据集2950001000圆环与圆3

1)改进算法参数对聚类性能影响分析。

影响算法聚类性能的主要参数为随机抽样次数m，图5显示参数m的变化与算法所需时间情况，其中数据集3为2个数据集的合集。可以看出，随着m增加，样本并集对原始自然簇的覆盖更加理想，但同时算法运行时间越来越长，随着m继续增加，算法时间的增加有所缓和，这主要因为单样本集聚类时采用并行算法，当样本集达到一定规模后，增加抽样次数对算法整体运行时间的影响不明显。

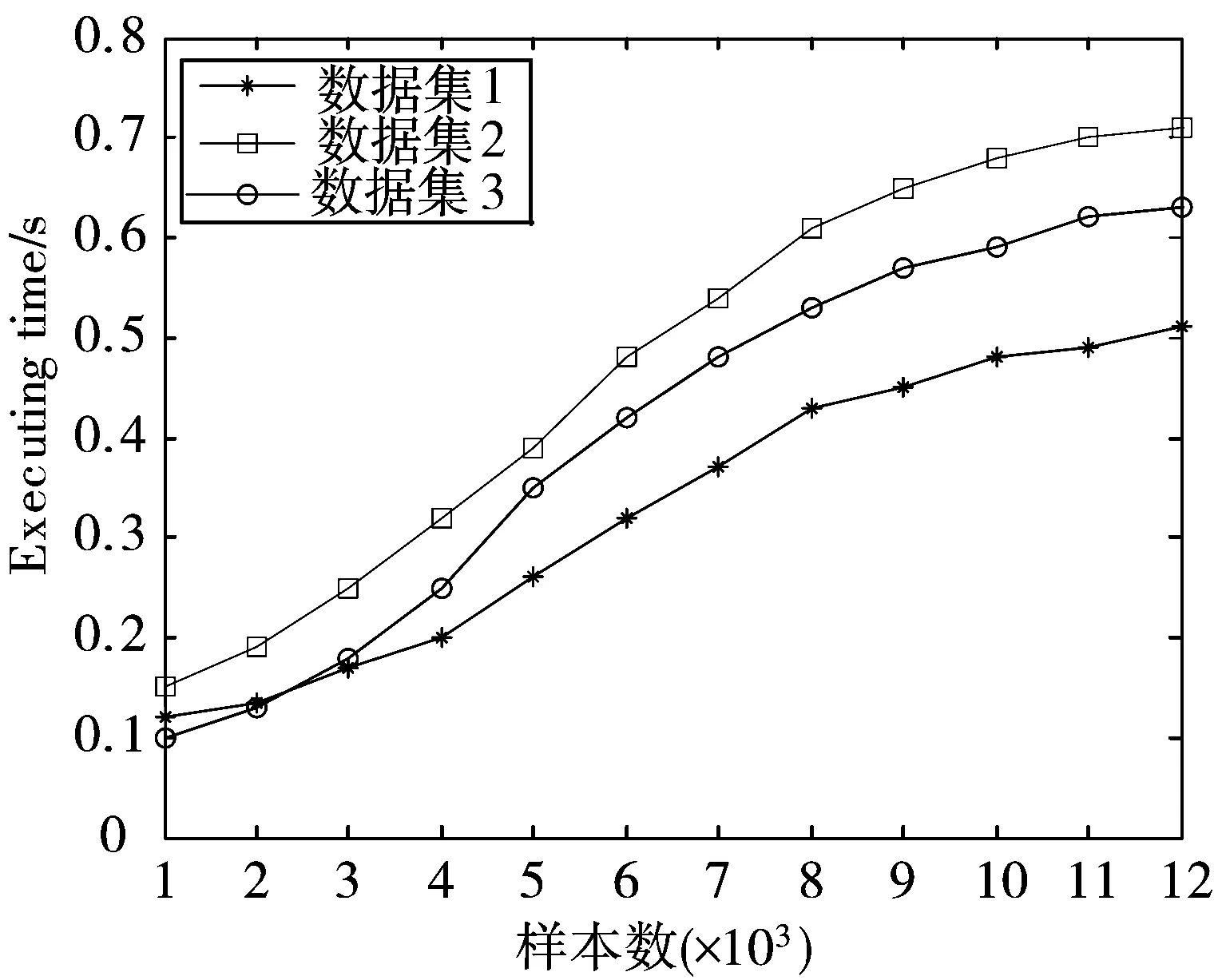
图5 3种算法运行时间随总样本数变化曲线

从实验结果可知，当m取较小值时，算法运行时间较少，但样本集难以区分原始数据集的聚类情况，而当m值增大，样本原始类别的覆盖更加理想，但运行时间也随之增加。因此m的选取要兼顾算法的聚类效果和运行时间。

2)聚类效果对比。

实验选用Rough-DBSCAN算法进行聚类效果对比。聚类效果的评价指标定义为非噪声点的分类准确率，记为F。

将Rough-DBSCAN算法与本文算法应用于图4的2个仿真数据集，并设置相同距离阈值T和邻域半径r，对2种算法的聚类结果如表2所示，可以看出，本文算法处理凸状数据集1和混合状数据集2时，其聚类的效果要优于Rough-DBSCAN算法。

表2 聚类效果对比实验结果

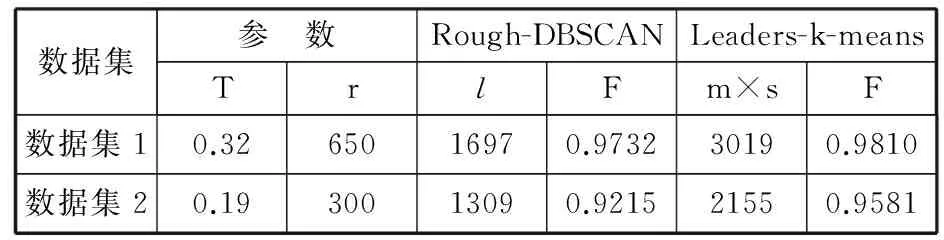
数据集参 数Rough-DBSCANLeaders-k-meansTrlFm×sF数据集10.3265016970.973230190.9810数据集20.1930013090.921521550.9581

3.2 真实的聚类实验分析

为保证财务审计数据的保密需要，本文针对企业利润问题，以营业收入增长率、营业利润增长率、利润总额增长率、净利润增长率作为分析指标，通过网络爬行技术选取2008～2015年度1079家沪市上市公司在互联网公开的财报数据作为研究样本，从中抽取并计算上述指标，形成有效实例数29650条，实验中算法迭代聚类次数设置为5次。

采用本文方法对数据聚类后，如图6所示为5次迭代后数据的聚类结果，可以看出根据4个指标上述数据被聚成5簇，第0簇4个指标都比较均衡，增长率在100%以下，其实例数占比为99.88%，而第1～4簇，其实例占比均在0.03%，且各指标之间变化异常，即为潜在的疑点小簇。

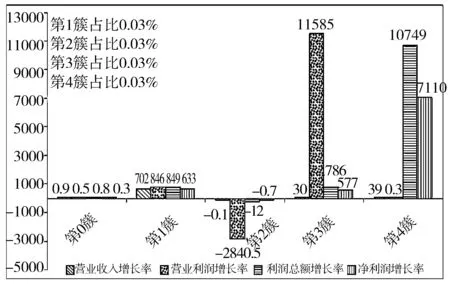
图6 5次聚类后各簇指标特点

第一次聚类发现的是可疑程度最高的公司，如图6中第3簇和第4簇中的实例，而第1簇中的实例，其上百倍利润增长率却易被增长率上万倍的公司所掩盖，因而第一次聚类时不易被检测出，但经过多次迭代聚类后，其异常值最终被聚出为疑点小簇。

根据实验聚类结果显示，上述1079家公司中共发现68家数据表现有异常的公司。

进一步通过证监会、上交所等机构公开的处罚信息对实验聚类疑点小簇进行验证，发现在68家可疑公司中，不少收到了上海交易所、证监会等的整改通知甚至是行政处罚，从而验证了本文算法对审计数据疑点发现的有效性。

另外，聚类挖掘的疑点公司并不都存在问题，其结果表明疑点小簇中的实例出现问题的概率更高，但最终的疑点确认需要审计人员完成。

4 结束语

为实现从海量数据中发现潜在的审计疑点，以辅助审计人员高效准确完成大数据审计，本文以聚类实例较少的小簇作为潜在的审计疑点，提出一种基于改进Leaders算子的审计大数据疑点发现算法，算法在Leaders算法自动完成审计大数据的初始聚类基础上，通过随机抽样融合方法对审计大数据的聚类结果进行优化，通过多次迭代聚类的方法，对实例数较少或可疑程度易被掩盖的小簇进一步聚类，从而实现对审计大数据的精确聚类，并以聚类实例较少的小簇作为潜在疑点，完成潜在审计疑点的发现。仿真数据实验和真实数据实验验证了本文算法的有效性。

参考文献：

[1] 程平,陈珊. 大数据时代基于DBSCAN聚类方法的审计抽样[J]. 中国注册会计师, 2016(4):76-79.

[2] 卢志茂,冯进玫,范冬梅,等. 面向大数据处理的划分聚类新方法[J]. 系统工程与电子技术, 2014,36(5):1010-1015.

[3] 余晓东,雷英杰,岳韶华,等. 基于粒子群优化的直觉模糊核聚类算法研究[J]. 通信学报, 2015,36(5):74-80.

[4] 王会金. 中观信息系统审计风险控制体系研究——以COBIT框架与数据挖掘技术相结合为视角[J]. 审计与经济研究, 2012,27(1):16-23.

[5] 秦志光,王士雨,赵洋,等. 云存储服务的动态数据完整性审计方案[J]. 计算机研究与发展, 2015,52(10):2192-2199.

[6] 秦荣生. 大数据、云计算技术对审计的影响研究[J]. 审计研究, 2014(6):23-28.

[7] 程平,范珂. 云会计环境下基于COBIT标准的“互联网+审计”模式研究[J]. 财务与会计, 2016(8):59-61.

[8] Ng R T, Han Jiawei. CLARANS: A method for clustering objects for spatial data mining[J]. IEEE Transactions on Knowledge and Data Engineering, 2002,14(5):1003-1016.

[9] Guha S, Rastogi R, Shim K. CURE: An efficient clustering algorithm for large databases[J]. Information Systems, 2001,26(1):35-58.

[10] Vijaya P A, Murty M N, Subramanian D K. Leaders-subleaders: An efficient hierarchical clustering algorithm for large data sets[J]. Pattern Recognition Letters, 2004,25(4):505-513.

[11] Viswanath P, Babu V S. Rough-DBSCAN: A fast hybrid density based clustering method for large data sets[J]. Pattern Recognition Letters, 2009,30(16):1477-1488.

[12] 杨蕴毅,孙中和,卢靖. 基于迭代式聚类的审计疑点发现——以上市公司财报数据为例[J]. 审计研究, 2015(4):60-66.

[13] 张琼,张莹,白清源,等. 一种新的基于粗糙集的leader聚类算法[J]. 计算机科学, 2008,35(3):177-179.

[14] 张燕平,张娟,何成刚,等. 基于佳点集与Leader方法的改进K-means聚类算法[J]. 计算机应用, 2011,31(5):1359-1362.

[15] 隋玉敏,孙秀芳,武优西,等. 负投影梯度的特征权重Leader聚类算法[J]. 小型微型计算机系统, 2014,35(9):2147-2150.

[16] 李斌,王劲松,黄玮. 一种大数据环境下的新聚类算法[J]. 计算机科学, 2015,42(12):247-250.

[17] HPC Lab. Frequent Set Counting[EB/OL]. http://miles.cnuce.cnr.it/～palmeri/datam/DCI/datasets.php, 2013-08-24.