浅谈物理选考综合题求解的步步深入
2018-05-09凌孝丽
凌孝丽
(浙江省新昌中学 310002)
解答物理综合题,就一般而言,涉及的知识点较多而且跨度大(需要用到力学和电学等多个知识领域的多个物理概念和规律),思维要求高(要求融合多种思维方式分析和解决问题),有时数学要求也高,因此,难度较大.对物理知识和方法掌握基础不是很好的绝大多数学生,解算物理综合题的初始阶段,往往困难较大.若把问题按物理过程发生的时间顺序分解为若干个小问题,而小问题的设计又做到由浅入深(先静态后动态,先简单后复杂,先定性后定量,先特殊后一般等),就能减低思维梯度(使解每个小题实际需要的思维结合度都处在学生的“最近发展区”内),从而化难为易,使绝大多数学生能顺利的或稍加提示能解算出所给的物理综合题,能有效减轻学生解算物理综合题的畏难情绪,提高解答综合题的自信心,激发积极性和创造性.训练一段时间后,逐步减少小题的数量,逐步加大思维梯度和物理知识综合度,以进一步培养学生物理知识的综合运用能力和物理思维(抽象思维、形象思维、直觉思维、发散聚合思维、辨证思维、纵横思维)的综合调控能力.
具体如何进行?现举几个例子加以说明,如下:
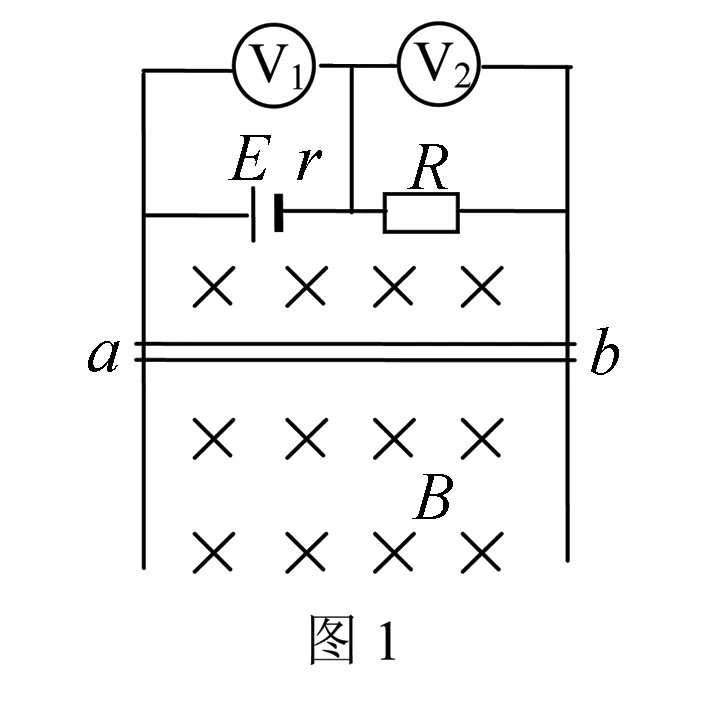
例1 如图1所示,竖直放置的两根足够长且平行的金属导轨相距L=0.50m,金属棒ab与导轨接触良好且可在导轨上无摩擦地滑动,ab棒质量为m=0.10kg,电阻Rab=0.50Ω,垂直于导轨水平放置.有一垂直于导轨平面的水平向里的匀强磁场,磁感应强度大小B=2.0T,电源电动势E=6.0V,内电阻r=0.50Ω,导轨电阻不计,电阻R=11Ω,取g=10m/s2(计算结果取两位有效数字).请求解下列各问:
(1)ab棒原先静止,求此时两电压表的示数.
解当ab棒静止时,ab棒虽处在磁场中,但没有动生电动势,仅是闭合电路中的一个外电阻,所求电路的外电路是一个纯电阻电路,电路中的电流强度为
I=E/(Rab+R+r)=6/(11+0.5+0.5)A=0.5A
电压表V1的示数即电源E的路端电压:U1=E-Ir(普适)
或U1=I(R+Rab)(外电路是纯电阻时适用)
电压表V2的示数为:U2=IR,
代入已知数据可算得:U1=5.75V,U2=5.5V.
解题总结:本小题是外电路属于纯电阻的闭合电路问题,所用的知识点有:闭合电路欧姆定律、部分电路欧姆定律和路端电压概念及其公式;能力要求:运用比较法区分定值电阻R上的电压与电源两端电压的不同求法及其适用性.
(2)松开ab瞬间,ab受哪些力作用?加速度大小和方向如何?它将向哪个方向运动?
解松开ab瞬间,ab速度仍为零,ab未切割磁感线,ab中仍没有动生电动势,闭合电路中的电流强度与第(1)问相同.ab受重力mg=1N,方向竖直向下;还受安培力F安=BIL=0.50N,方向竖直向上.ab受合力F合=mg-F=0.5N,方向竖直向下,加速度a=F合/m=5m/s2,方向竖直向下,所以ab将由静止开始向下作加速运动.
(3)在ab运动过程中,它的加速度如何变化?速度如何变化?
解设ab运动t时间后的速度为v,ab切割磁感线产生的动生电动势为E动生=BLv,方向为a指向b,与闭合电路中的电源电动势E方向相同,电路中的电流为I=(E+BLv)/(Rab+R+r),
ab受的安培力为
F安=BIL=BL(E+BLv)/(Rab+R+r),
ab的加速度为
a=(mg-F安)/m=[mg-BL(E+BLv)/(Rab+R+r)]/m
随着v的增大,a不断减小,但因a与v同向,所以速度v增大,当a减小到零时,速度达到最大,以后ab以最大速度做匀速运动.
(4)在ab运动过程中,两电压表的示数如何变化?
解当ab棒运动时,由第(3)问知:I=(E+BLv)/(Rab+R+r)
U1=E-Ir,[请注意:U1=I(R+Rab)不成立,因为ab棒运动时,切割磁感线存在动生电动势,它是一个电源,不是纯电阻了)
U2=IR
在ab运动过程中,v先增大,达到最大后不变,则I先增大后不变,U1先减小后不变,U2先增大后不变.
(5)当ab棒下滑速度为2m/s时,ab棒的加速度多大?两表的读数各多大?
解由第(3)问知,a=(mg-F安)/m=[mg-BL(E+BLv)/(Rab+R+r)]/m
代入已知数据可算得:a=3.33m/s2.
I=(E+BLv)/(Rab+R+r)=(6+2×0.5×2)/(0.5+11+0.5)A=2/3A
U1=E-Ir=[6-(2/3)×0.5]V=5.67V
U2=IR=(2/3)×11V=7.33V
(6)在什么条件下,ab棒下滑的速度达到最大?最大速度为多少?
当ab棒加速度减少到零时,速度达最大.由第(3)问知,
a=(mg-F安)/m=[mg-BL(E+BLv)/(Rab+R+r)]/m,
令a=0得:mg=BL(E+BLvm)/(Rab+R+r)
∴vm=[mg(Rab+R+r)-BLE]/B2L2
代入已知数据,可算出
vm=6m/s.
例2 如图2所示,在x轴上方有磁感应强度为B的匀强磁场,x轴下方有电场强度为E的匀强电场.有一带负电的粒子质量为m,带电量为q,重力不计.
(1)将带电粒子自y轴上离O点下方L远处的A点由静止释放,求带电粒子到达O点时速度的大小.
解带负电粒子在电场中受到电场力作用而加速,运动L距离后到达O点,其速度可用动能定理求得:
qEL=mv02/2,
∴v0=(2qEL/m)1/2
(2)带电粒子进入磁场后运动的轨道半径多大?
解带电粒子从O点向上进入匀强磁场后,在洛仑兹力作用下做匀速圆周运动,
qv0B=mv02/R,R=mv0/qB
=(m/qB)(2qEL/m)1/2=(1/B)(2mEL/q)1/2
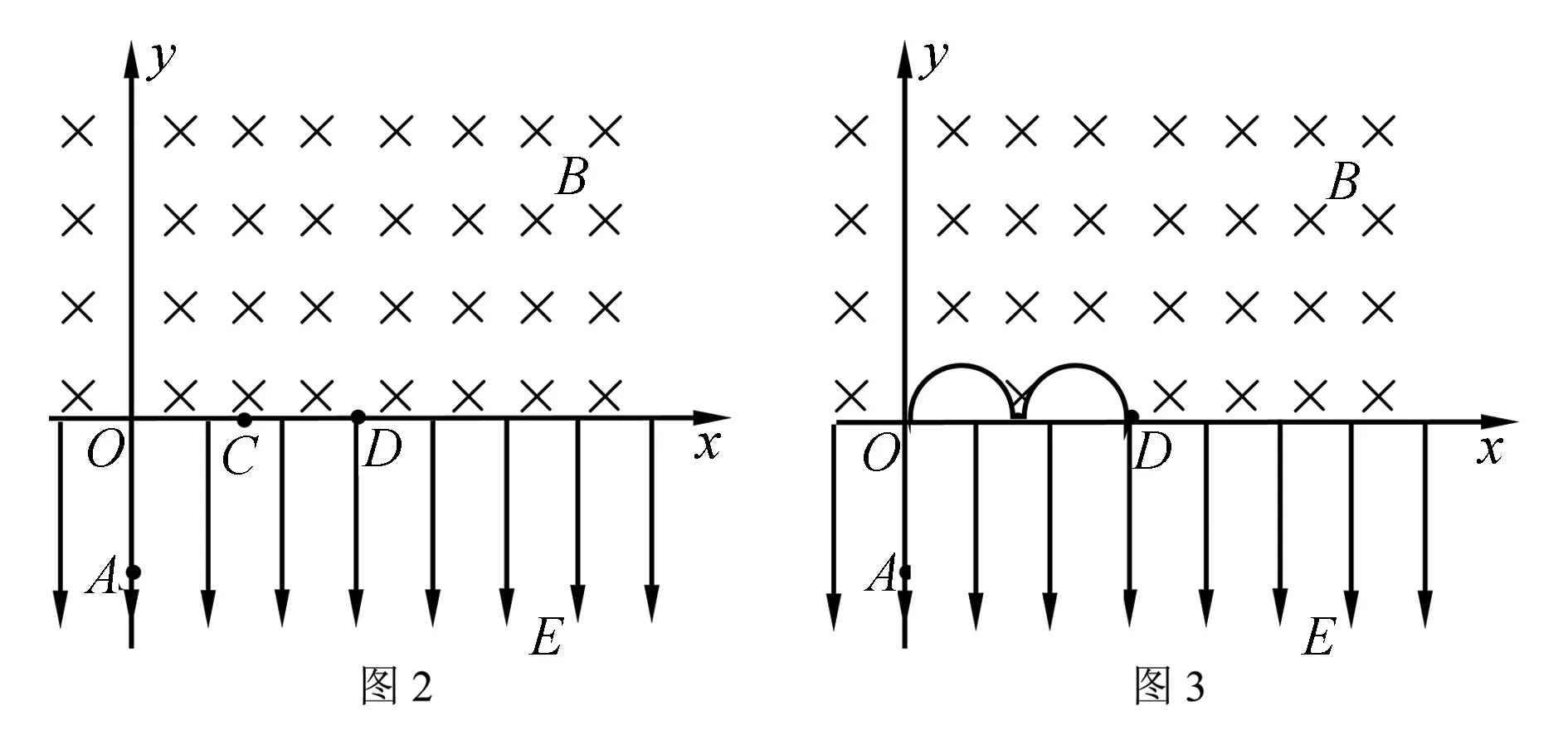
(3)带电粒子经过x轴上一点C,C点离O点多远?
解:带电粒子从O点向上进入匀强磁场后,向右偏转做匀速圆周运动,经过半个周期后通过x轴上的C点,C点离开O点的距离为:
OC=2R=(2/B)(2mEL/q)1/2
(4)带电粒子从C点重新进入电场后,经多长时间又返回C点?
解法一带电粒子从C点重新进入电场后做匀减速直线速运动,当速度减小到零后,又返回来从静止开始做匀加速直线运动,所需时间可由牛顿第二定律结合运动学公式求解:v0=at0=qEt0/m,
解出t0=mv0/qE=(m/qE)(2qEL/m)1/2=(2mL/qE)1/2
往返的总时间为:t=2t0=2(2mL/qE)1/2.
解法二对带电粒子用动量定理可得:
qEt0=mv0
t0=mv0/qE=(2mL/qE)1/2
∴往返的总时间为:t=2t0=2(2mL/qE)1/2.
(5)带电粒子从C点重新进入磁场后又一次经过x轴上的D点,D点距O点多远?(如图3所示)
解带电粒子以速度v0从C点重新进入磁场后,在洛仑兹力作用下,又向右做匀速圆周运动,再经过半个周期又回到x轴上的D点,D点离O点的距离应为轨道半径的4倍,即
OD=4R=(4/B)(2mEL/q)1/2
(6)带电粒子从y轴上A点开始运动到x轴上D点一共用多少时间?
解带电粒子从y轴上A点开始运动到x轴上D点的时间包括在匀强电场中运动的时间是
t1=3t0=3(2mL/qE)1/2,
带电粒子在匀强磁场中运动的时间是半周期的2倍,即一个周期:
t2=T=2πm/qB,
所以,带电粒子从A点运动到D点的总时间为:
t=t1+t2=3(2mL/qE)1/2+2πm/qB
(7)如果要使带电粒子从y轴上A点由静止释放,能够击中x轴上的G点,G点距O点的距离为d,那么带电粒子在磁场中的轨迹半径多大?
解要使带电粒子从O点进入磁场后,能击中x轴上距O点为d的G点,则只能使OG的1/n等于粒子运动半径R的两倍即可,其中n为正整数,即d/n=2R,∴R=d/2n(n=1,2,3,…)
(8)在上一小题中,带电粒子在磁场中运动的速度多大?
解洛仑磁力提供向心力:qvB=mv2/R
∴带电粒子的速度为:v=qBR/m=(qB/m)(d/2n)=qBd/2nm(n=1,2,3,…)
(9)试确定A点的位置.
解由动能定理可得:qE·OA′=mv2/2,
∴OA′=mv2/2qE=(m/2qE)(qBd/2nm)2=B2d2q/8n2mE(n=1,2,3,…)
(10)在第(7)小题中,带电粒子从A′点开始运动到击中G点一共需要多少时间?
解带电粒子从A点开始运动,到击中G点,在电场中运动的时间为:t1=(2n-1)t0
由动量定理得qE·t0=mv=m·qBd/2nm=qBd/2n
∴t0=qBd/2nqE=Bd/2nE
于是可得t1=(2n-1)t0=(2n-1)Bd/2nE=[(2n-1)/2n]Bd/E(n=1,2,3,…)
带电粒子在磁场中运动的时间为
t2=n·T/2=n·T/2=n·(2πm/qB)/2=nπm/qB(n=1,2,3,…)
∴带电粒子从A点运动G点的总时间为
t=t1+t2=[(2n-1)/2n]Bd/E+nπm/qB(n=1,2,3,…)

例3 (原创题)、两根足够长倾斜角为θ的固定平行金属导轨上端连接一阻值为R的电阻,如图4所示,导轨电阻可忽略,导轨宽为L,整个导轨平面内分布着磁感应强度大小为B,方向垂直于导轨平面向上的匀强磁场.一质量为m、与导轨垂直搁置、连入电路的电阻为r的金属棒ab,与导轨间的动摩擦因数为μ,在平行于导轨平面向上的恒拉力F作用下,由静止开始沿倾斜轨道向上滑动,当向上滑动s1距离时金属棒ab的速度刚好达到最大值,就在此刻立即撤去F,之后金属棒ab再上滑s2距离其速度变为零.求:(1)金属棒ab的最大速度和电阻R的最大发热功率;(2)金属棒ab在上滑的全过程中,动生电动势提供的总电能,克服安培力做的功和内外电阻上的总发热量.
解(1)设金属棒ab在s1段运动的某一时刻的速度为v,则电路中的感应电流为
I=BLv/(R+r)
金属棒ab受的安培力为:F安1=BIL=B2L2v/(R+r)

金属棒ab受力情况如图5所示,根据牛顿第二定律得
F-mgsinθ-f滑-F安1=ma1
即F-mgsinθ-μmgcosθ-B2L2v/(R+r)=ma1①
随着v的增大,a减小,当a=0时,速度达到最大.
令a=0,由①式可得金属棒的最大速度为
vm=(F-mgsinθ-μmgcosθ)(R+r)/B2L2②
此时,金属棒ab切割磁感线产生的动生电动势最大,
电路中的感应电流最大,电阻R的发热功率也最大.
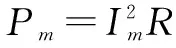
Im=BLvm/(R+r) ④
由②③④可解得
Pm=(F-mgsinθ-μmgcosθ)2R/B2L2
(2)由F安1=B2L2v/(R+r)式可知,金属棒ab在上滑的全过程中,速度变化,安培力是变力,无法用功的定义式求解克服安培力做的功.用能量守恒定律解比较简便.
对金属棒ab的上滑全过程:假设轨道区域无磁场,那么,金属棒上滑过程无须克服安培力做功,也没有电能产生,是个纯力学问题,因为始末状态速度均为零,所以,拉力做的功应等于克服重力和滑动摩擦力做的功,从能量角度看,即通过拉力做功外界转化来的能量分成了两部分能量:重力势能增加量和滑动摩擦发热量.
本题存在磁场,是个发电机模型题.金属棒切割磁感线产生了动生电动势,为电路提供了电能,通过拉力做功外界转化来的能量分成了三部分能量:重力势能增加量,滑动摩擦发热量和动生电动势提供的总电能.因此,动生电动势提供的总电能为
ΔE电能=E外界-EP重增-E摩擦热
即ΔE电能=F·s1-mg(s1+s2)sinθ-μmgcosθ(s1+s2)
克服安培力做的功或内外电阻上的总发热量与动生电动势提供的总电能相等.
总之,在物理解题教学过程中,可引导学生把综合性较强的难题分解为几个小问题,一步步由浅入深,使学生更深刻的理解、掌握物理概念及其规律,形成科学的解题程序、思路和方法,领悟形成这种解题思路和方法的科学根据,掌握解题的一般规律性,积累大脑中储存的解题依据、方法、经验等,优化物理解题思想,提高学生针对实际问题,分析物理现象、认定物理事实、揭示物理本质的功力和提出问题、分析问题、解决问题的能力.同时,发展、增强学生的物理抽象思维的深刻性、形象思维的动态性、直觉思维的独创性、辨证思维的合理性、纵横思维的策略性、顺逆聚散思维的方向性,优化和提升学生物理解题的创造性思维能力.
参考文献:
[1]屠凌云,何理. 浙江省普通高中学科教学指导意见[M]. 杭州:浙江教育出版社,2014.
[2]阎金铎. 中学物理教材教法[M]. 北京:北京师范大学出版社,2002.
[3]刘爱伦. 思维心理学[M].上海:上海教育出版社,2002.
