基于熵权集结交叉评价模型的洪灾脆弱性评价

李 璐，高 睿，汪 洋

(武汉大学 土木建筑工程学院， 湖北 武汉 430072)

洪水灾害作为影响范围最广、影响程度最深的自然灾害之一，对其防范与控制一直是防灾减灾工作的重点，亦引起了学术界的密切关注与研究[1]。目前，基于脆弱性的自然灾害研究[2]在指导防灾减灾工作方面已经起到越来越重要的作用。脆弱性起源于“致灾因子论”，而不同于致灾因子论中“致灾因子的强度及频率决定灾害的严重程度”的观点，以脆弱性为基础的灾害研究从承灾体的视角出发分析问题[1]。本文参考相关文献定义脆弱性如下：区域承灾体内人类活动受自然灾害影响的程度[2]。

指标体系法是目前评价脆弱性最常用的方法之一，其通过建立特定指标体系来实现对不同区域承灾体的脆弱性进行评价和比较。但是，指标体系法存在的问题较为明显，即指标权重的客观性问题，影响评价结果的可信度。数据包络分析方法(DEA)基于投入-产出的相对有效性，无需人为预估权重等，可以有效避免主观因素影响，提升评价的客观性，目前已经在公共交通、产业效率、城市发展和银行业等领域广泛应用，如朱燕飞等[3]、张昆等[4]均将其运用于水资源效率评价研究，一些学者将这种基于投入-产出的模型引入洪水灾害脆弱性评价中，如刘毅等[5]、程翠云等[6]、裴欢等[7]。其用于洪灾脆弱性评价的基本思路为：将洪灾看作一个系统，由各输入因素(致灾因子等)的综合作用形成灾害(输出结果)。洪灾脆弱性越大，洪灾形成的效率越高，灾害形成后的灾情越严重[8]。

本文在既有研究的基础上，运用数据包络分析方法，构建了洪灾脆弱性评价指标体系；针对传统数据包络分析模型无法进一步评价样本，引入交叉评价思想，建立了基于交叉评价思想的洪水灾害脆弱性模型，应用距离熵集结交叉效率的方法最大限度区分样本，使得洪水灾害脆弱性综合评价和区划更加合理，对洪灾预警、防洪减灾决策等具有指导性意义。

1 洪水灾害区域脆弱性评价模型

1.1 CCR模型

假设有n个决策单元，每个样本有m个输入、s个输出，记第j(j=1,2…,n)个样本的第i(i=1,2…,m)个输入xij和第r(r=1,2,...,s)个输出yrj。假设第k个决策单元为被评价决策单元，νk和μk为相应的权重系数，其中νk=(ν1k,ν2k，…，νmk)T，μk=(μ1K，μ2k，…，μsk)T，求解DMUk的效率值CCR模型如下：

(1)

μrk≥0，r=1，2，…,s；vik≥0，i=1,2,…,m

式中：Ekk表示第k个洪灾单元的成灾效率。

模型(1)求解n次，得到n个决策单元的自评效率值。当效率值为1时，该决策单元有效；否则，该决策单元无效。

1.2 交叉效率模型

基于自评的交叉效率(CCR)模型将决策单元分为有效决策单元和无效决策单元。问题在于，当CCR模型同时存在多个有效决策单元时，将难以区分。因此，相关学者[9]在此基础上建立了基于他评的交叉效率模型：

(2)

模型(2)中Etk是用第t个决策单元的最优权重求出的第k个决策单元的效率值。

依据交叉效率模型计算得到交叉效率矩阵：

(3)

1.3 熵模型

熵的概念最初来源于热力学，Shannon首次将熵引入通讯工程，提出一种能够度量系统状态的信息熵。熵是对系统不确定性的度量，且呈正相关。结合信息熵的定义[10-13]提出第j个属性下第i个评价单元交叉效率Eij熵值的定义：

(4)

引入距离熵的概念，第i个评价单元他评效率和自评效率的距离熵函数定义如下：

dij=hij-hjj，j=1,2…,n

(5)

函数(5)中，hij是DMUj的他评交叉效率，hjj是DMUj的自评交叉效率。

距离熵的实际意义在于距离熵的值越小，自评和他评效率之间的不确定性越小，亦即一致性越好，集结权重也越大。评价单元DMUk各他评效率集结权重按如下公式计算：

(6)

采用线性加权的方法整合自评效率和他评效率得到最终成灾效率，评价单元DMUk综合成灾效率计算公式如下：

(7)

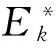
1.4 熵权集结改进DEA交叉效率模型

将CCR模型于距离熵集结模型进行结合，得到评价自然灾害区域脆弱性的改进DEA交叉效率模型。模型的基本结构和评价步骤如下：

① 量化评价指标及处理相应数据，详见2.1。

② 使用交叉效率模型(2)，通过自评权重计算他评效率，形成交叉效率矩(3)。

③ 利用距离熵模型(5)、(6)和线性加权模型(7)集结交叉效率，得到优化后的决策单元区域成灾效率。

④ 成灾效率排序及结果分析。

2 实例分析

2.1 指标选取与处理

本文以2011年到2015年全国31个省市的洪水灾害情况数据为依托。一般，洪灾危险性选用洪灾频次和洪涝灾害的规模，两者的综合集中反应为洪水灾害的灾变程度[14]，故选取历史灾变程度作为洪灾危险性指标；洪灾暴露性选取人口数量、耕地面积、经济总量为指标；损失程度选取受灾人口、受灾面积和直接经济损失作为指标。

2.2 评价准备

为了进行该评价，需要先使用到CCR-DEA模型。该模型的前提假设为：输出随输入的增加而增加[15]。因此，需用SPSS软件将输入与输出数据进行Pearson相关性验证。将上述指标数据输入软件，分析得到Pearson相关性系数，如表1所示。

如表1所示，各输入输出项均呈正相关；耕地面积与受灾耕地在0.01水平上(双侧)显著相关，而与受灾人口和直接经济损失的关系不显著，理论上应舍弃，但考虑到耕地面积大小与洪灾之间的关系，此处予以保留；人口数量、生产总值、历史灾度均与受灾耕地面积、受灾人口、直接经济损失显著相关，予以选用。本次评价有4个输入项、3个输出项，并有31个洪灾单元，满足受评DMU个数至少为输入个数与输出个数和的两倍的检验法则。

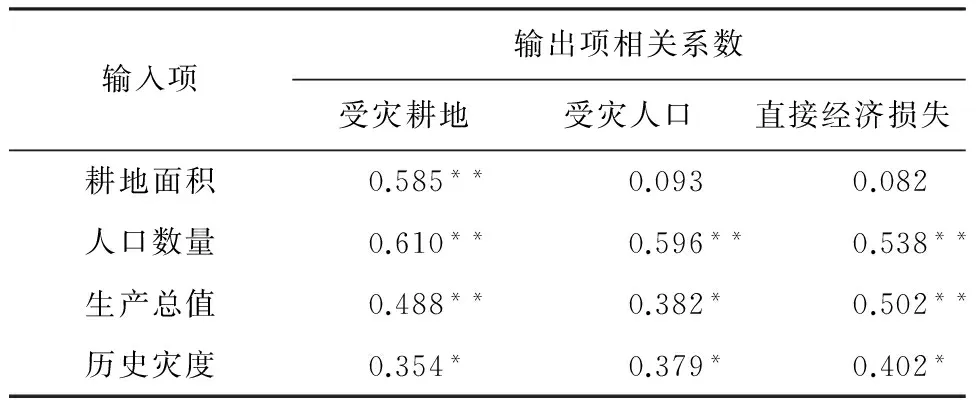
表1 全国各省输入项与输出项相关系数表

注：**.在0.01水平上(双侧)显著相关；*.在0.05水平上(双侧)显著相关。

2.3 求解改进交叉效率及分析

将31个省、直辖市的输入和输出数据带进CCR-DEA模型中，计算得到各省、直辖市的全局成灾效率。再将上述指标带入基于熵权集结改进DEA交叉效率模型中，利用Deap、MATLAB以及Excel进行数据处理，得出各省份水灾的全局成灾效率。最后，比较两计算结果，见表2。

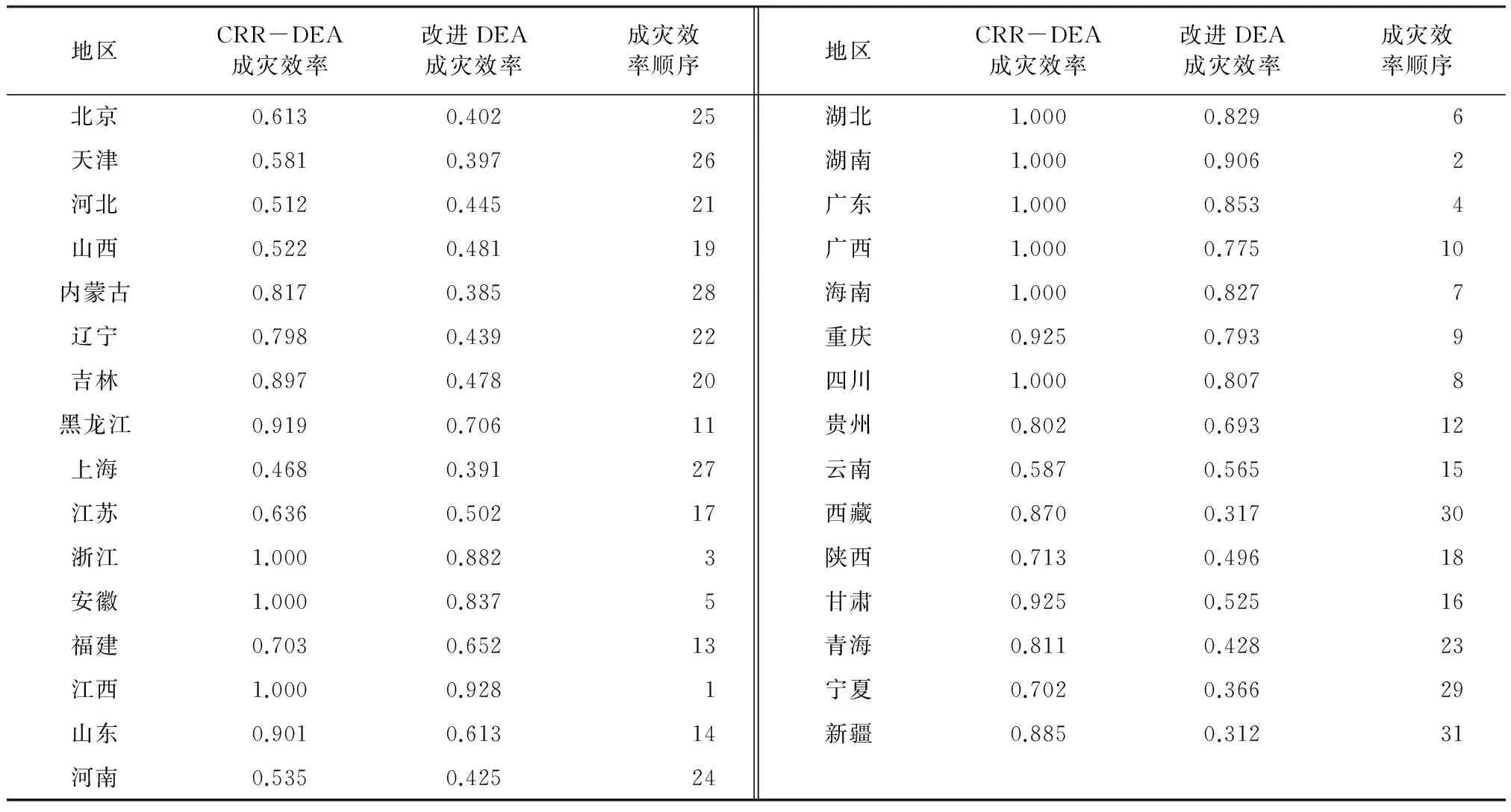
表2 全国各省洪水灾害区域脆弱性评价表

从表2中可以发现，由基于熵权集结改进DEA模型得出的成灾效率在各省的排序结果与CCR-DEA所得的排序结果相似，仅在个别省份因数据样本采集或地区的差异的原因造成了一定的偏差。同时基于熵权集结改进DEA模型克服了CCR-DEA模型无法将成灾效率较高的省份区别开来的不足，将CCR-DEA模型中多个成灾效率为1.000的省份进行了成灾效率的排序。查阅相关资料表明，该计算结果与实际情况也相符。将成灾效率数据代入曲线图中，如图1所示，可以发现基于熵权集结改进DEA模型曲线更趋于平缓。

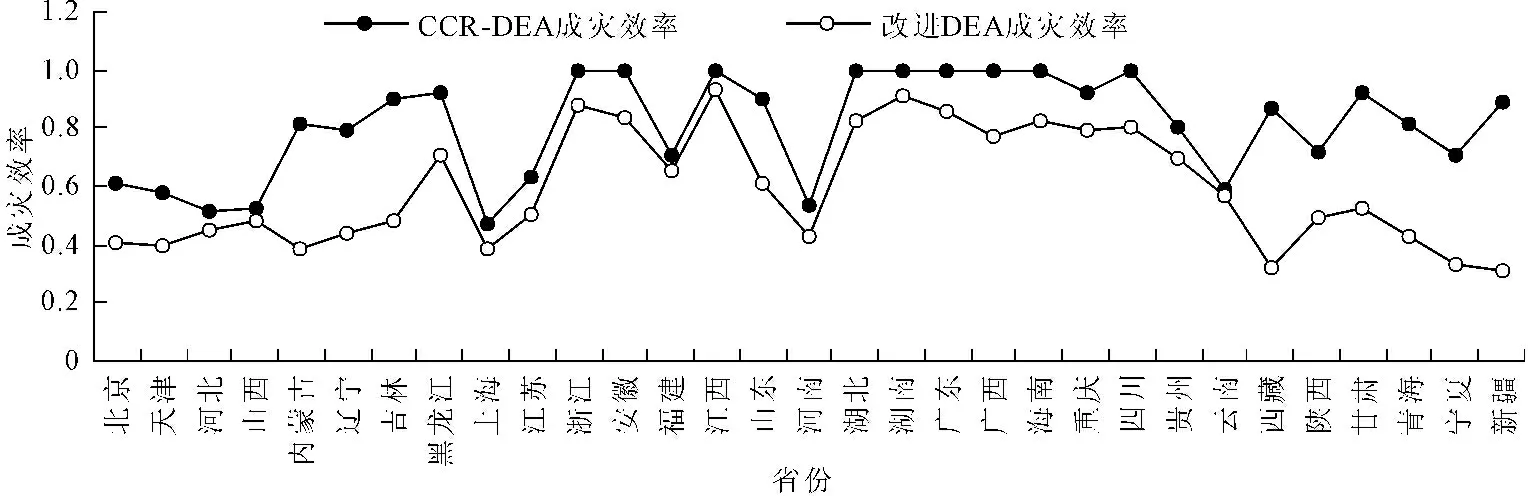
图1 DEA模型脆弱性对比图

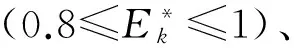
表3 全国各省成灾分布表

3 结 论

(1) 将DEA交叉效率模型与距离熵相结合得到的基于熵权集结改进DEA交叉效率模型得到的评价结果与CRR-DEA及实际情况一致，说明该方法是可行的。

(2) 将DEA交叉效率模型与距离熵相结合得到的基于熵权集结改进DEA交叉效率模型，解决了传统DEA模型中极端权重分配的问题，在实际应用中更具有实用性。

(3) 将DEA交叉效率模型与距离熵相结合得到的基于熵权集结改进DEA交叉效率模型为解决洪灾脆弱性评价提供了一种新思路，同时也为传统DEA方法求解提供了一种新思路。

参考文献：

[1] 阮平平,贾艾晨.Google Earth在城市洪灾分析中的应用研究[J].水利与建筑工程学报,2013(6):213-216.

[2] 曾家俊,黄华爱,刘 松，等.广西德保岩溶内涝灾害成因分析[J].水利与建筑工程学报,2015(6):118-122.

[3] Pelanda C. Disaster and Sociosystemic Vulnerability[M]． Gorizia: Disaster Research Center, 1981.

[4] Wisner B, Blaikie P, Cannon T, et al. At Risk: Natural Hazards, People’s Vulnerability and Disasters[M]. London: Routledge，1994.

[5] 朱燕飞,陈智和,金远征.金华市水资源利用效率评价研究[J].人民长江,2016,47(21):43-47.

[6] 张 昆,马静洲,吴泽斌，等.长江经济带11省市水资源利用效率评价[J].人民长江,2015,46(18):48-51.

[7] 刘 毅,黄建毅,马 丽.基于DEA模型的我国自然灾害区域脆弱性评价[J].地理研究,2010,29(7):1153-1162.

[8] 程翠云,钱 新,盛金保，等.基于数据包络分析的溃坝洪水灾害脆弱性评价[J].水土保持通报,2010,30(3):144-147，157.

[9] 裴 欢,王晓妍,房世峰.基于DEA的中国农业旱灾脆弱性评价及时空演变分析[J].灾害学,2015,30(2):64-69.

[10] 温 宁,刘铁民.基于对抗交叉评价模型的中国自然灾害区域脆弱性评价[J].中国安全生产科学技术,2011,7(4):24-28.

[11] Sexton T R, Silkman R H, Hogan A J. Data envelopment analysis: Critique and extensions[J]. New Directions for Program Evaluation, 1986(32):73-105.

[12] Wang Y M, Wang S. Approaches to determining the relative importance weights for cross-efficency aggregation in data envelopment analysis[J]. Journal of the Operational Research Society, 2013,64(1):60-69.

[13] Wu J, Sun J S, Liang L, et al. Determination of weights for ultimate cross efficiency using Shannon entropy[J]. Expert Systems with Applications, 2011,38(5):5162-5165.

[14] 唐言明,白 夏,卜 松，等.基于广义联系度函数的城市防洪标准方案优选模型[J].水利与建筑工程学报，2016,14(2):178-181.

[15] 孙加森.数据包络分析(DEA)的交叉效率理论方法与应用研究[D].合肥:中国科学技术大学,2014:41-48.