基于水平条分与斜条分相结合的边坡稳定性解析计算

邱 超，王平安，苏 茹，刘建元

(西安建筑科技大学 土木工程学院， 陕西 西安 710055)

地震作用对边坡稳定性的影响很大[1]。尤其是在山区和丘陵地带，由地震作用导致的边坡失稳具有数量多和危害大等特点[2]，因此，地震作用下的边坡稳定性分析一直是岩土工程界的重要课题之一[3-4]。

地震荷载作用下的边坡稳定性问题一直是岩土工程中的研究难点[5]。目前，地震荷载作用下边坡稳定性分析方法主要有：拟静力法[6-9]、滑块分析法[10]、动力时程分析法[11-12]、有限单元法[13]以及离散元法[14]等。由于拟静力法具有有效与易于操作等特点，因而逐渐被广泛学者采用。在边坡稳定性分析的拟静力法研究当中，通常在土条上施加地震力，来分析边坡的稳定性。运用不同的边坡稳定性分析方法，对应着不同的拟静力分析的形式，邓东平等[15-16]采用任意滑动面搜索方法，对地震作用下边坡的稳定性进行拟静力分析。邓东平等[17]采用拟静力分析方法分析了不同滑动面型式下边坡的稳定性。Ausilio E等[8]应用运动极限分析定理，采用拟静力法分析了加筋土坡的稳定性。陈昌富等[18]通过对土条进行水平条分，运用遗传算法对边坡稳定性进行了拟静力分析。在将水平条分法应用到分析加筋土坡的稳定性分析过程当中[19-21]，都假定边坡潜在滑动面不经过坡角，不是针对一般的边坡滑动面，邓东平等[22]采用水平条分与斜条分相结合的方法很好地解决了水平条分法的缺陷。但是对于均质土坡而言，水平条分和斜条分需要分开计算，且土条划分宽度严重影响计算的精度与工作量。因此，有必要对地震作用下边坡滑动面经过坡角这一情况进行地震作用下边坡稳定性分析。

本文采用解析计算的方法，通过引入竖向中心角，将水平条分和斜条分统一起来计算，大大减少了计算量。基于拟静力分析法，采用积分的方法建立了地震作用下边坡安全系数的解析表达式。编制了相关的程序对地震作用下边坡稳定性问题进行了优化求解，并且分析了水平荷载作用系数、竖向荷载作用系数以及比例系数对边坡安全系数与边坡潜在滑动面的影响。

1 基本假定

1.1 基本假定

如图1所示，均质边坡，潜在滑动面为圆弧滑动面，滑动面圆心O，半径r0，边坡高度H，坡角θ，土体重度γ，内摩擦角φ，黏聚力c。x0、y0分别为边坡滑动面圆心的横、纵坐标。D、F分别为过C、A两点竖直线与潜在滑动面的交点。μ为G点的横坐标，α1、α2、η1、η、β分别为G、F、D、E、B对应于O点的竖向中心角，φ为边坡滑动面上任意一点对应于O点的竖向中心角，顺时针为正。在分析问题之前做如下几点基本假定：

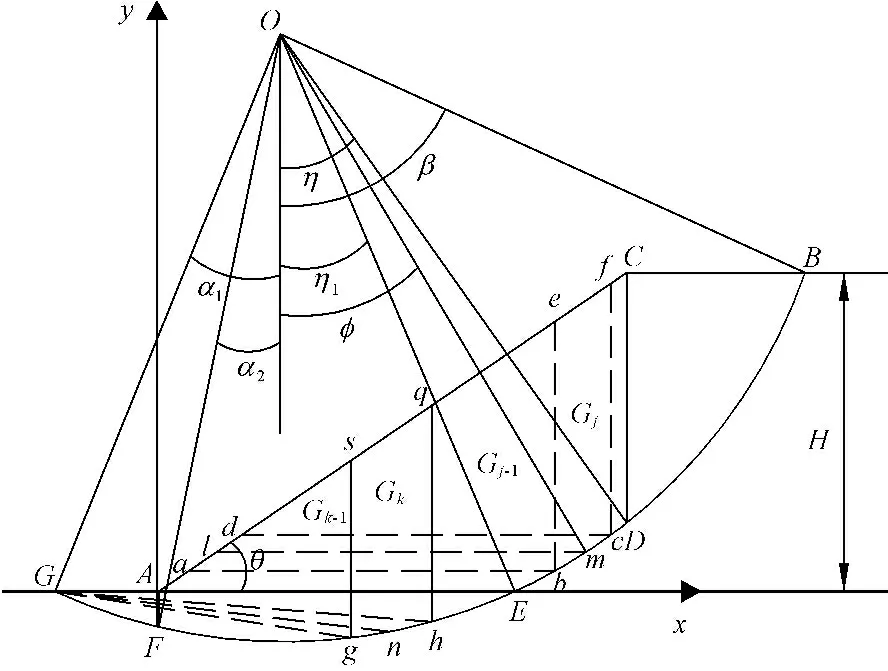
图1滑动面参量示意图

(1) 对于水平条和斜条而言，土条竖直方向的荷载等于上覆荷载，在地震作用下上覆荷载等于(1+kv)Wi；水平荷载等于khWi。

(2) 边坡滑动面为圆弧，且边坡潜在滑动面上安全系数相同。

(3) 边坡土体满足摩尔-库仑屈服准则，即

τf=σtanφ+c

(1)

式中：τf、σ分别为边坡破坏时，滑动面上的切应力和正应力。

1.2 条间力假定

在边坡稳定性分析当中，采用水平条分法与斜条分法结合起来分析边坡。对于一般滑动面的边坡，对边坡脚趾以上的土体，采用水平条分；对边坡脚趾以下的土体，采用斜条分；水平土条和斜土条受力示意图见图2(a)和图2(b)。根据Shangholi M等[19]对条间力的假定，水平土条条间力有如下关系：

(2)

式中：Vj、Vj-1分别为竖向条间力；Hj、Hj-1分别为水平条间力；Gj、Gj-1分别为条块def和abe的重力。

为了得到斜土条条间力的关系，对块体GhqA和sghq进行受力分析，见图3(a)和图3(b)。由静力平衡关系得：

(3)

由式(3)反解出Xk、Ek，有：

(4)

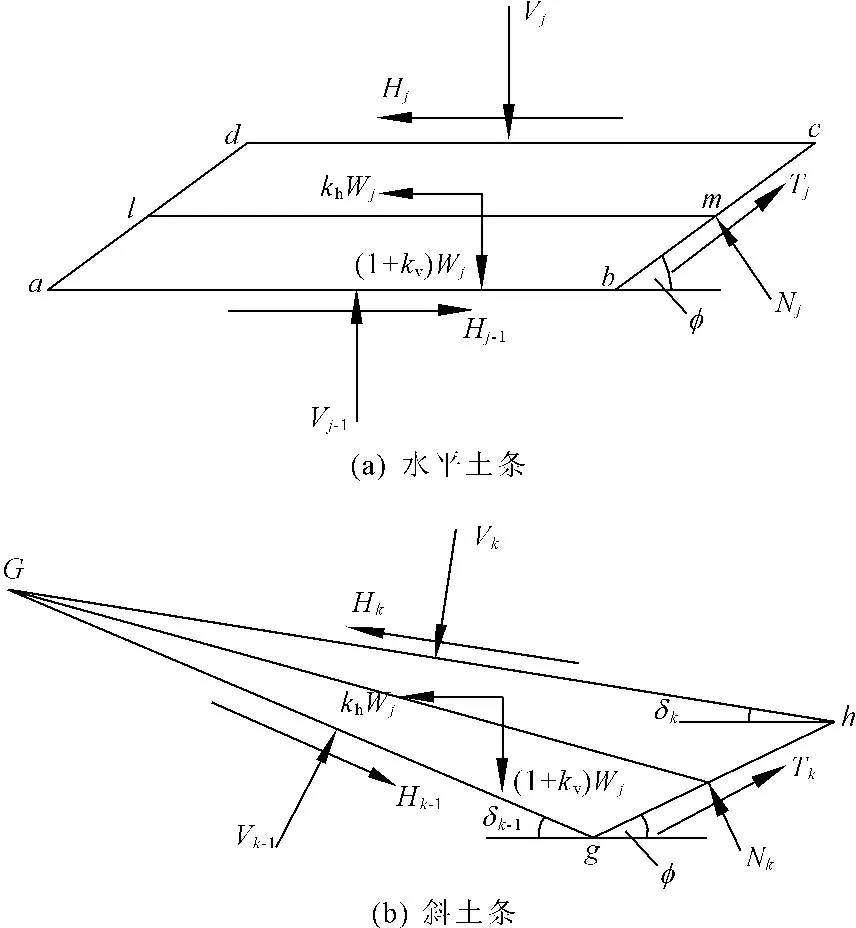
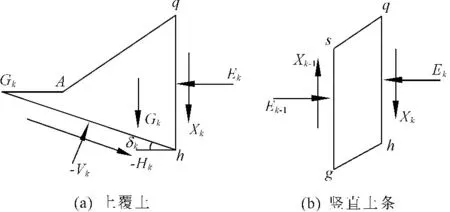
图2 水平土条、斜土条受力分析

图3土条受力分析

本文在分析边坡稳定性分析过程当中，采用Bishop对条间力的假定，于是条间力有如下关系：

(5)

式中：Ek、Ek-1为条块sghq所受的水平条间力；Xk、Xk-1为条块sghq所受的竖向条间力。

将式(5)带入式(4)中有：

(6)

式中：Vk、Vk-1为斜条块Ggh上、下两个底面的正向力；Hk、Hk-1为条块Ggh上、下两个底面的切向力；Gk，Gk-1分别为块体GhqA、GgsA的重力。δk、δk-1分别为斜条块上、下两个底面与水平方向的夹角，逆时针为正。

2 安全系数解析计算

由图2(a)和图2(b)考虑条块水平向与竖向静力平衡，有：

(7)

Nk=Hk-1sin(δk-1+φ)-Vk-1cos(δk-1+φ)-Hksin(δk+φ)+Vkcos(δk+φ)+Wkcosφ

Tk=-Hk-1cos(δk-1+φ)-Vk-1sin(δk-1+φ)+Hkcos(δk+φ)+Vksin(δk+φ)+Wksinφ

(8)

式中：Wj、Wk分别为水平条和斜体的重力。Nj、Tj分别为水平条上的切向力和法向力，Nk、Nk-1分别为斜条上的切向力和法向力。将式(2)、式(6)分别带入到式(7)、式(8)中，得到如下关系：

(9)

考虑地震荷载作用下的边坡稳定性，对条块进行受力分析，有：

Ticosφ-Nisinφ-khWi=0

Tisinφ+Nicosφ-(1+kv)(Wi+Gi-Gi-1)=0

(10)

反解出Ti、Ni，有：

(11)

式中：kh为水平荷载作用系数；kv为竖向荷载作用系数。

根据，安全系数等于抗滑力与下滑力之比，有：

(12)

式中：li为土条底面长度；n为划分的土条数。

为了更加精确的分析边坡稳定性，采用积分的办法代替条分，由图1得到(Gi-Gi-1)与Wi的表达式分别为：

Gi-Gi-1=

(13)

(14)

联立式(13)、式(14)有：

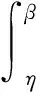
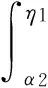
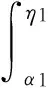
(15)

注意到，边坡滑动面上任意一点的坐标可以表示为：

(16)

由图1几何关系，竖向中心角，可以表示为：

(17)

反解出x0，y0，r0，有：

(18)

联立式(12)、式(13)、式(14)、式(15)、式(18)，安全系数可以表示为：

(19)

式中：

sinα1

(20)

(21)

(22)

(23)

为了得到边坡安全系数的最小值，以及对应的边坡潜在滑动面，本文应用MATLAB软件，编制了相关的优化程序进行求解，式(19)的安全系数为中心角α1、α2、η1、η、β的函数，该问题为非线性约束问题，约束条件为：

(24)

3 算例分析

为了验证本文方法和编制优化程序的正确性，静态条件下，对已有的典型算例进行计算，对比结果见表1。由表1可知，本文方法与简化Bishop法所获得的安全系数很接近。说明不考虑地震效应作用下，本文方法是有效的。

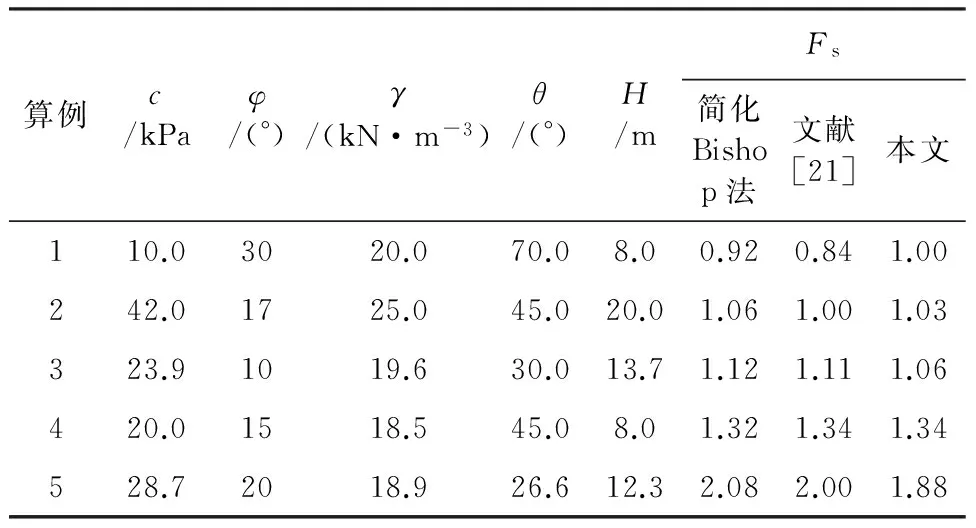
表1 安全系数结果对比

边坡坡高H=8 m，坡角θ=15°，岩土参数为：γ=20 kN/m3，c=30 kN/m3，φ=10°。当kv=0，kh分别取0.00、0.10、0.20、0.30，罗强等[23]采用对数螺旋滑动面时极限上限法计算得到的安全系数分别为4.400、3.120、2.390、1.920，邓东平等[15]采用滑动面搜索新方法计算得到的安全系数分别为4.318、2.968、2.229、1.769，本文方法计算得到的安全系数分别为4.119、2.884、2.184、1.773。本文方法计算得到的安全系数与文献[15]计算得到的安全系数十分接近，且略小一些。因而，说明本文方法分析边坡稳定性是安全有效的。

4 影响因素参数分析

一般情况下，在地震作用下边坡稳定性分析过程中，水平地震作用系数与竖直作用系数有如下关系：kv=ξkh(其中，ξ为kv相对于kh的比例系数)。取边坡参数为：边坡坡高H=10 m，边坡坡角θ分别为30°、45°和60°，重度为γ=18 kN/m3，黏聚力c为30 kPa，内摩擦角为30°。为了分析地震作用下边坡的稳定性，对水平地震作用系数kh分别取0.05、0.10、0.15、0.20、0.25和0.30，比例系数ξ取-1.0、-0.5、0.0、0.5、1.0。不同θ值下，地震效应对安全系数的影响见图4，临界滑动面见图5。

从图4和图5可知，一定ξ值下，安全系数Fs随着水平地震系数kh的增大而减小，当kh一定时，边坡临界滑动面随着竖向地震系数的减小，边坡潜在滑动面逐渐变深，边坡失稳的范围越来越大，且随着kh的增大，这种趋势越明显。

5 结 论

(1) 采用水平条分与斜条分相结合的方法，对地震作用下边坡稳定性进行分析，通过引入竖向中心角，建立了安全系数的解析算式。通过编写优化程序，采用MATLAB中Fmincon函数对问题进行优化求解，与多个算例对比验证了本文方法和优化程序的有效性。

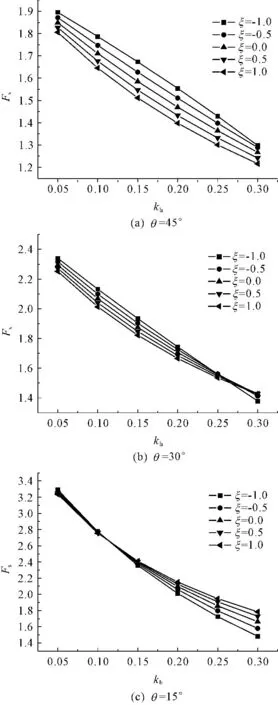
图4不同θ下地震效应对安全系数的影响

(2) 一定ξ值下，安全系数Fs随着kh的增大而减小，水平地震系数kh与比例系数ξ对边坡潜在滑动面有着显著的影响。当kh一定时，边坡临界滑动面随着比例系数ξ的减小，边坡潜在滑动面逐渐变深，边坡失稳的范围越来越大，且随着kh的增大，这种趋势越明显。

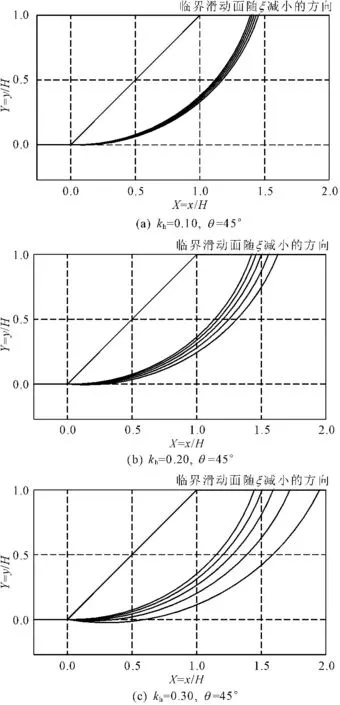
图5不同kh下地震效应对边坡潜在滑动面的影响

参考文献：

[1] 郑颖人,叶海林,黄润秋.地震边坡破坏机制及破坏面的分析探讨[J].岩石力学与工程报,2009,28(8):1714-1723.

[2] 夏栋舟,刘建华,何忠明.强震作用下岩质高边坡动力特性[J].中南大学学报,2012,43(6):2396-2402.

[3] 赵 博，赵亚琼.边坡稳定性能的判定方法研究及其工程应用[J].水利与建筑工程学报，2017,15(1):25-29.

[4] 李 闯，赵盛杰，董 晔，等.Fellenius法的解析算法[J].水利与建筑工程学报，2016，14(5):202-210.

[5] 郑颖人,叶海林,黄润秋，等.边坡地震稳定性分析探讨[J].地震工程与工程振动，2010,30(2):173-180.

[6] 罗红明,唐辉明,胡 斌，等.考虑地震力的刚体极限平衡法及工程应用[J].岩石力学与工程学报,2007,26(S1):3590-3595.

[7] Radoslaw L, Michalowski. Soil reinforced for seismic design of geotechnical structures[J]. Computers and Geotechnics, 1998,23(1):1-17.

[8] Ausilio E, Conte E, Dente G. Seismic stability analysis of reinforced slope[J]. Soil Dynamics and Earthquake Engineering, 2000,19(3):159-172.

[9] Nimbalkar S S, Choudhury D, Mandal J N. Seismic stability of reinforced-soil wall by pseudo-dynamic method[J]. Geosynthetics International, 2006,13(3):111-119.

[10] Michalowski R L, You L Z. displacements of reinforced slopes subjected to seismic loads[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000,126(8):685-694.

[11] 黄 诚，王安明，任伟中.水平向与竖向地震的时间耦合模式对边坡动力安全系数的影响[J].岩土力学,2010,31(11):3404-3410.

[12] 刘汉龙，贵 康，高玉峰.边坡地震稳定性时程分析方法[J].岩土力学，2003,24(4):553-557.

[13] 张国栋，刘 学，金 星，等.基于有限单元法的岩土边坡动力稳定分析及评价方法研究进展[J].工程力学，2008，25(S2):44-52.

[14] 谭儒姣，李明生，徐鹏逍，等.地震作用下边坡岩体动力稳定性数值模拟[J].岩土力学与工程学报,2009,28(S2):3986-2992.

[15] 邓东平，李 亮.基于滑动面搜索新方法对地震作用下边坡稳定性拟静力分析[J].岩石力学与工程学报，2012,31(1):86-98.

[16] 邓东平，李 亮,罗 伟.地震作用下土钉支护边坡稳定性拟静力分析[J].岩土力学,2012,33(6):1787-1794.

[17] 邓东平，李 亮，赵炼恒.地震作用下边坡稳定性分析的拟静力法研究[J].中南大学学报，2014,45(10):3578-3588.

[18] 陈昌富，杨 宇，龚晓南.基于遗产算法地震荷载作用下边坡稳定性分析水平条分法[J].岩石力学与工程学报，2003，22(11):1919-1923.

[19] Shangholi M, Fakher A, Jones Cjfp. Horizontal slice method of analysis[J]. Geotechnique, 2001,51(10):881-885.

[20] Nouri H, Fakher A, Jones Cjfp. Evaluating the effects of the magnitude and amplification of pseudo-static acceleration on reinforced soil slopes and walls using the limit equilibrium horizontal slicesmethod[J]. Geotextiles and Geomembranes, 2008,26(3):263-278.

[21] Nouri H, Fakher A, Jones Cjfp. Development of horizontal slice method for seismic stability analysis of reinforced slopes and walls[J]. Geotextiles and Geomembranes, 2006,24(3):175-187.

[22] 邓东平，李 亮.水平条分法下边坡稳定性分析与计算方法研究[J].岩土力学,2012,33(10):3179-3188.

[23] 罗 强，赵炼恒，李 亮，等.地震效应和边坡超载对均质土坡稳定性影响的拟静力分析[J].岩土力学,2010,31(12):3835-3848.