新旧混凝土凹凸咬合界面剪切滑移的破坏形态与承载力分析

吴二军，张能伟

(河海大学 土木与交通学院， 江苏 南京 210098)

新旧混凝土的界面承载力是结构物修补与加固工程中的一个重要指标[1]，现有文献中基于试验提出的多种新旧混凝土界面受剪承载力计算公式计算结果差异较大，且不能揭示其剪切滑移全过程的受力机理[2]。基于新旧混凝土界面的剪切滑移受力机理对界面受剪承载力进行分析是一个可行的重要方法，但由于界面剪切问题的复杂性，目前研究较少且远未成熟。

Brikeland P W等[3-4]在1966年提出了新旧混凝土界面的摩擦抗剪理论，该理论将界面钢筋达到屈服时的界面摩擦力作为其极限承载力，并在此基础上提出了配筋新旧混凝土界面抗剪强度的计算表达式。此后，众多学者对新旧混凝土界面抗剪机理和强度计算表达式进行了深入研究[5-9]。Alan H等[5]研究了界面正应力σn对界面承载力的影响。Loov R E[6]研究了混凝土强度fc对界面承载力的影响。郭进军等[10]通过试验研究了界面粗糙度对界面粘结抗剪强度的影响。范亮[11]进行了32个试件的先后浇混凝土界面抗剪试验研究，在参考试验结果以及国内外已有的试验数据的基础上建立了界面抗剪强度通用计算公式。张雷顺等[12]进行了8组植筋新旧混凝土粘结试件的抗剪试验，得到了植筋界面的粘结剪切强度和植筋率的关系表达式。

本文以简单规则的新旧混凝土凹凸界面为研究对象，深入探讨其破坏过程,分析界面受剪滑移过程及可能的破坏形态，并根据不同破坏形态分别分析其受剪承载力的计算方法。

1 规则齿咬合新旧混凝土界面的受力状态

1.1 研究对象的确定

设规则齿咬合的新旧混凝土双剪面受剪构件，横截面尺寸(宽×高)为b×h，齿根部截面高hV。界面上受到压力Fc约束，Fc=σs0As，As、σs0分别为穿过界面形心的钢筋(简称穿界面钢筋)截面面积和初始应力。界面两侧受到相对剪力作用，剪跨接近于零，试件如图1所示。

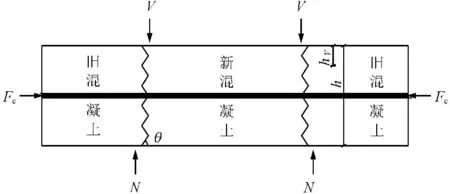
图1规则齿咬合新旧混凝土双界面试件受力示意图

1.2 界面剪切滑移过程及破坏形态

郭进军等[10]研究认为，新旧混凝土界面抗剪强度明显低于一次整体浇筑混凝土，因此，当图1所示构件加载时，初始破坏面首先出现在齿咬合界面上。随着荷载增加，新旧混凝土接触界面出现裂缝，界面两侧混凝土相互滑移错开。继续加载，试件将达到承载能力极限状态而发生破坏。其可能的破坏形态有四种：

(1) 齿剪断破坏：随着滑移变形的增加，相互咬合的齿受剪高度减小，发生剪断破坏(见图2(a))。

(2) 过缝钢筋剪断破坏：穿过界面的横向钢筋较多，凸齿倾角较大时，齿剪断后承载力继续提高，界面相对滑移变形增长，直至穿过界面的钢筋被剪断(见图2(b))。

(3) 过缝钢筋拉断破坏：穿过界面的横向钢筋较多，凸齿倾角较小时，齿剪断后承载力继续提高，界面相对滑移变形增长，直至穿过界面的钢筋被拉断(图2(c))。

(4) 齿滑脱(剪摩擦)破坏：当齿高很小，穿过界面的钢筋配置过少时，钢筋达到抗拉屈服强度 ，甚至可能拉断破坏，由于水平位移较大，齿滑开，咬合失效(见图2(d))。

1.3 滑移过程中界面的受力状态

在界面滑移过程中，黏聚力失效，界面抗剪能力主要由摩擦力和齿咬合作用承担，受力状态如图3所示。

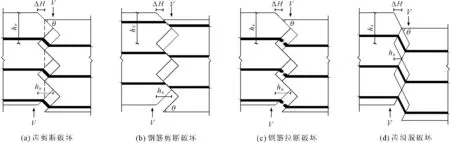
图2四种破坏模式的示意图

图3中，Ffi为新旧混凝土界面摩擦力；Fni为新旧混凝土界面压力；Fs为穿界面钢筋所受的拉力；FsV为界面上的剪力作用，其值很小，通常可忽略不计；α为界面滑移后，穿界面钢筋的弯折角度，钢筋与混凝土交界区域的混凝土可能会被压酥，导致α<θ，为简便计算，可取α=θ；ΔL为穿界面钢筋伸长量；ΔH为界面滑移水平分量。穿界面钢筋拉力由式(1)计算。

(1)

式中，Ls0为穿界面钢筋滑移伸长影响范围内的初始长度。对于无粘结钢筋混凝土构件，Ls0为钢筋的初始长度；对于有粘结钢筋混凝土构件，Ls0与钢筋锚固长度、混凝土强度等因素有关，其计算较为复杂，为简化计算，本文仅考虑钢筋与混凝土的无粘结情况。对于图3所示的界面受力状态，外加剪力与界面提供剪切抗力、界面压力与穿过界面钢筋应力满足式(2)(竖直方向)、式(3)(水平方向)所示的平衡关系。

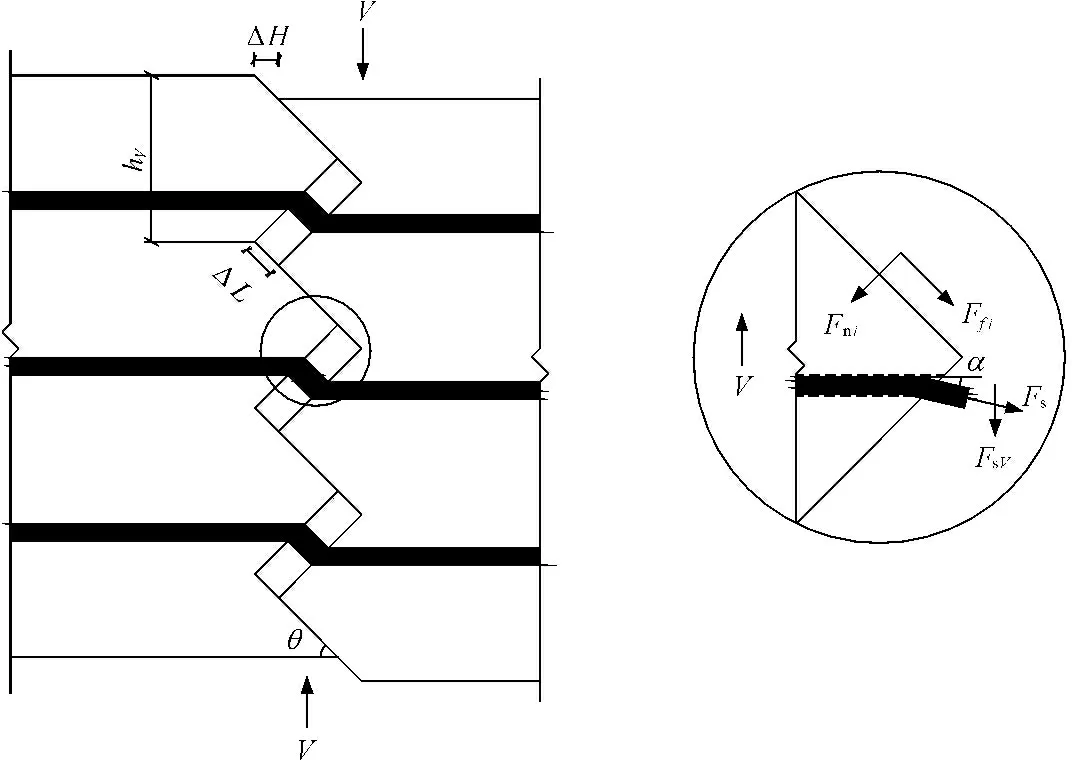
图3界面滑移后齿咬合界面受力分析示意图

V=VcV+VsV=∑Fnicosθ+∑Ffisinθ+∑Fssinα

(2)

∑Fscosα=∑Fnisinθ-∑Fficosθ

(3)

其中，VcV=∑Fnicosθ+∑Ffisinθ，为作用在混凝土齿上的竖向剪力；Ffi=μFni，μ为混凝土之间的摩擦系数。由式(2)、式(3)得：

V=∑(κcosα+sinα)Fs

(4)

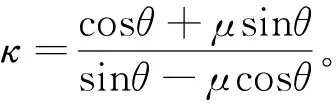
由式(2)、式(4)得：

VcV=∑κcosαFs

(5)

2 四种破坏形态的承载力计算表达式

2.1 第一种破坏形态的承载力计算表达式

当作用在混凝土上的竖向剪力达到混凝土齿提供的抗剪承载力时，混凝土齿即被剪断，此时穿界面钢筋尚未达到其屈服强度，即发生第一种破坏形态。构件的承载力由混凝土和钢筋共同提供。

Vu1=Vcu+Vsu

(6)

文献[13]指出混凝土抗剪试件达到其极限强度时，试件塑性变形很小，可采用弹性理论分析计算。因此假设混凝土齿间与齿内的剪应力分布均符合中部大、边缘小的抛物线分布。混凝土的剪切破坏受主拉应力控制，纯剪应力状态与二轴受力状态等效，主拉强度与单轴抗拉强度值接近。所以混凝土的纯剪强度可近似等于单轴抗拉强度[14]，由此得混凝土齿提供的抗剪承载力为

(7)

式中，ζ为正应力对抗剪强度的影响系数，该效应与作用在界面上的正压力有关。

混凝土齿发生剪断破坏时，界面钢筋尚未达到其屈服强度，此时Vcu=VcV、Vsu=VsV=∑Fssinα，由式(5)得：

(8)

将式(7)、式(8)代入式(6)得：

(9)

2.2 第二种破坏形态的承载力计算表达式

当穿过界面的横向钢筋较多且凸齿倾角较大时，钢筋在外荷载作用下可能发生剪断破坏。由图2(b)可知，横向钢筋剪断模式的承载力同样由两部分组成，咬合界面的摩擦力和钢筋受剪承载力。

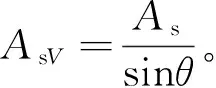
则界面摩擦力提供的受剪承载力为：0.58μ2cosαfyAs，取α=θ得第二种破坏模式下的构件承载力为：

Vu2=fyAs(0.58μ2cosα+0.58)

(10)

式中：μ2为混凝土齿剪断后的界面摩擦系数。

2.3 第三种破坏形态的承载力计算表达式

当穿过界面的横向钢筋较多但凸齿倾角较小时，钢筋在外荷载作用下可能发生拉断破坏。当穿界面钢筋发生拉断破坏时，构件的承载力由钢筋的屈服强度决定，此时钢筋拉力的竖向分量为fyAssinα，由此得构件的承载力为：

Vu3=fyAs(μ2cosα+sinα)

(11)

2.4 第四种破坏形态的承载力计算表达式

当发生第四种破坏形态时，界面两侧的水平位移过大，相互咬合的齿滑脱失效。界限条件是ΔH=hh，根据图2中的几何关系和物理方程可得此时界面钢筋的应力：

(12)

将式(12)代入式(1)得：

(13)

代入式(4)得：

(14)

3 四种破坏形态的判别条件

3.1 四种破坏形态的定性判断

由前述分析知，当hh>[hh]、As>[As]时，可能发生破坏形态一；当hh>[hh]、As<[As]、θ>[θ]时，可能发生破坏形态二；当hh>[hh]、As<[As]、θ<[θ]时，可能发生破坏形态三；当hh<[hh]、ft>[ft]时，可能发生破坏形态四；当hh<[hh]、ft<[ft]时，仍可能发生破坏形态一。

3.2 第一种破坏形态的发生条件

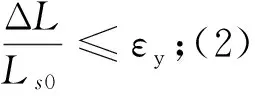
对于受拉钢筋不屈服，根据式(1)、式(7)、式(8)，得：

(15)

(16)

此处的hh也即实际工程结构中的界面凿毛深度。由式(16)得：

(17)

3.3 第一种破坏状态和第二、三种破坏状态的界限

3.3.1 第二种破坏形态和第三种破坏形态的界限

第二种破坏形态和第三种破坏形态均以界面钢筋发生破坏为标志。令Vu2=Vu3得：当θ=20°时，穿界面钢筋处于界限破坏状态；当θ>20°时，剪切破坏起控制作用；当θ<20°时，受拉破坏起控制作用，此时，[θ]=20°。

此外，发生第二种破坏形态和第三种破坏形态的前提条件是界面不滑脱，即需满足式(16)。

3.3.2 第一种破坏形态和第二种破坏形态的界限

第一种破坏形态和第二种破坏形态的界限是Vu1=Vu2，将式(9)、式(11)代入得到界限破坏状态的界面配筋面积：

(18)

3.3.3 第一种破坏形态和第三种破坏形态的界限

第一种破坏形态和第三种破坏形态的界限是Vu1=Vu3，将式(9)、式(11)代入得到界限破坏状态的界面配筋面积：

(19)

综上，当As≥[As]时，发生第一种破坏形态；当As<[As]且θ>[θ]时，发生第二种破坏形态；当As<[As]且θ<[θ]时，发生第三种破坏形态，其中[As]=max{As1,2，As1,3}。

3.4 第一种破坏形态和第四种破坏形态的界限

当发生第四种破坏形态时，界面两侧相互咬合的齿失效，此时ΔH≥hh，也即：

(20)

第一种破坏形态和第四种破坏形态的界限是Vu1=Vu4，将式(9)、式(14)代入得到界限破坏状态的混凝土抗拉强度：

(21)

当ft≥[ft]时，发生第四种破坏形态，当ft<[ft]时，发生第一种破坏形态。

3.5 四种破坏形态判别流程

试件可能发生的四种破坏形态的判断流程如图4所示。

也可根据试件的已有尺寸和参数，分别计算上述推导的四种破坏形态的承载力Vu1、Vu2、Vu3、Vu4，构件的实际承载力受四种破坏形态承载力的最小值控制，对应于最小承载力的破坏形态也即试件最终发生的破坏形态。

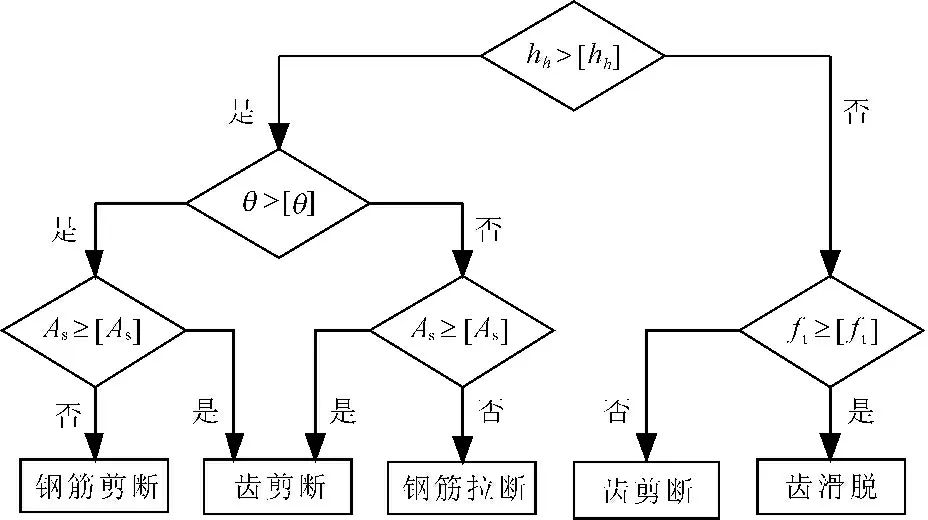
图4破坏形态判断流程图

4 承载力试验值与计算值对比

文献[15]中做了不同齿根宽度和锯齿高度的试验，混凝土强度等级选用C30，穿界面钢筋采用原长为550 mm的体外无粘结滑移钢筋，试验中，穿界面钢筋仅提供横向约束作用，并不随界面的滑移而弯折，故不提供竖向抗剪作用，Vu1应采用式(7)计算，其他试验参数见表1。

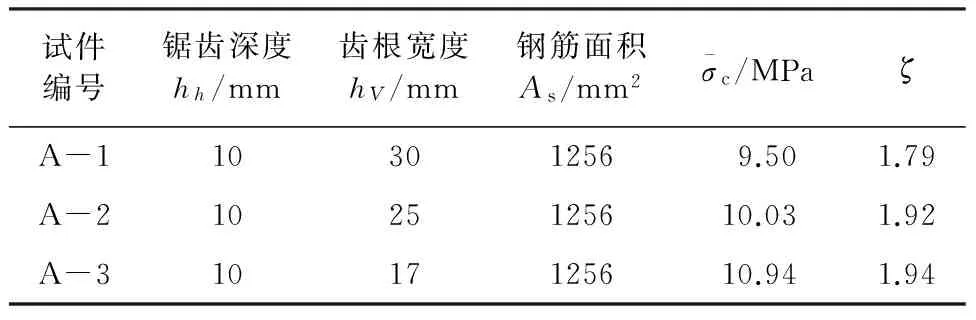
表1 试件参数表

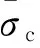
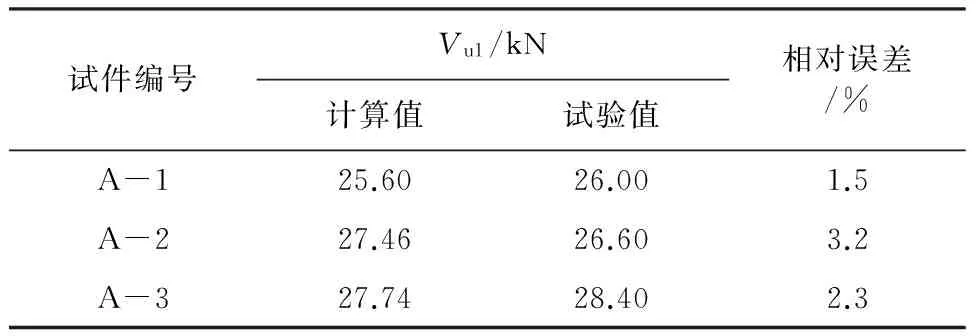
表2 承载力计算值与试验值对比

表2结果表明，根据剪切滑移机理推导的承载力公式计算结果与试验值相对误差在5%以内，说明本文的承载力计算公式有一定合理性。

5 结 论

通过对规则齿咬合新旧混凝土界面的受力性能分析，可以得到以下结论：

(1) 规则齿咬合构件在外荷载作用下有四种破坏形态：混凝土齿剪断破坏、界面钢筋剪断破坏、界面钢筋拉断拉断、齿滑脱破坏。

(2) 根据每种破坏形态的受力特征，分别建立其承载力计算表达式。通过对四种破坏形态界限的分析，得出发生每种破坏形态的判别条件。

(3) 将本文承载力公式计算结果与试验值进行对比，发现两者相对误差在5%以内，说明采用本文的承载力计算公式具有一定的合理性。

参考文献：

[1] 曹宏亮，史长城，郭旭东，等.第二龄期老混凝土与新混凝土粘结劈拉强度研究[J].水利与建筑工程学报，2016，14(6):102-106.

[2] 王怀亮，田 平.动态压剪作用下碾压混凝土强度和变形研究[J].水利与建筑工程学报，2016，14(2):18-24.

[3] Birkeland P W, Birkeland H W. Connections in precast concrete construction[J]. ACI Journal Proceedings, 1966，63(3):345-368.

[4] Birkeland P Patnaki A H. Horizontal shear strength of composite concrete beams with a rough interface[D]. Ph.D. thesis, Canada:University of Calgary, 1992.

[5] Mattock A H. Shear transfer in reinforced concrete-recent research[J]. PCI Journal, 1972，17(2):55-75.

[6] Loov R E. Design of precast connections[C]//Paper Presented at A Seminar Organized by Compa International Pt,Ltd. Singapore, 1978.

[7] Randl N. Investigations on transfer of forces between old and new concrete at different joint roughness[D]. Ph.D. thesis. Austria: University of Innsbruck, 1997.

[8] The International Federation for Structural Concrete (FIB). Model Code 2010. First complete draft-vol[S]. Secretariat Permanent, Case Postale 88, CH-1050 Lausanne, Switzerland, 2010.

[9] Loov R E, Patnaki A K. Horizontal shear strength of composite concrete beams with a rough interface[J]. PCI Journal, 1994，39(1):48-69.

[10] 郭进军，王少波，张雷顺，等.新老混凝土粘结的剪切性能试验研究[J].建筑结构，2002,32(8):43-45．

[11] 范 亮.先后浇混凝土界面抗剪性能研究[D].重庆：重庆大学，2004．

[12] 张雷顺，王二花，闫国新.植筋法新老混凝土粘结面剪切性能试验研究[J].郑州大学学报(工学版)，2006,27(3):34-37．

[13] 王传志，藤智明主编.钢筋混凝土结构理论[M].北京：中国建筑工业出版社，1985:54-55.

[14] 张 琦，过镇海.砼抗剪强度和剪切变形的研究[J].建筑结构学报，1992,13(5):17-24．

[15] 张 盼.接触面分布特征对新旧混凝土界面强度的影响分析[D].南京：河海大学，2016．