泥水盾构下穿引起上覆砌体结构响应的实测分析

林存刚

(1.同济大学 地下建筑与工程系，上海 200092； 2.同济大学 岩土及地下工程教育部重点实验室， 上海 200092)

伴随国内盾构隧道工程的大量涌现，泥水盾构下穿既有建筑物的案例愈发多见。虽然泥水盾构在地层沉降控制方面较传统隧道工法更具优势，但仍不可避免地引发地层位移，进而导致邻近建筑物变形。上覆建筑物在隧道开挖地层损失下的形变响应取决于土与结构的相互作用，该问题向来是理论研究和工程实践中的热点。

极限拉应变法广泛应用于砌体结构在不均匀沉降下的损伤评估[1-4]。该方法将原位地层沉降施加于建筑物，由此计算其拉应变，进而评估其损伤程度。Potts D M等[5]将土与结构相互作用融入极限拉应变法，对建筑物及土体刚度开展了参数分析。Franzius J N等[6-8]进一步考虑了建筑物重量及地基与基础接触面特性等因素的影响。

理论解析方法便于工程应用，被广泛应用于地基不均匀沉降下既有建筑物的损伤评估。Deck O等[9]提出了一种计算隧道施工引起建筑挠曲的理论方法，该方法将地基和结构分别简化为Winkler地基和弹性梁。Boone S J[10]提出了一种评估地基不均匀沉降对建筑物损伤的评估方法。Finno R J等[11]提出了评估隧道开挖引起建筑物损伤的复合梁方法。Schuster M等[12]建立了一种评估基坑开挖引起建筑物损伤的简单模型。

除了理论解析和数值模拟之外，原位监测和模型试验亦是探究隧道施工引发上覆建筑物响应的有效手段，如Dimmock P S等[13]对伦敦地铁Jubilee线延伸段隧道施工中上覆建筑物的变形进行了大量的实测研究。而模型试验可对影响建筑物响应的关键因素进行可控条件下的深入分析，可用来验证理论解析及数值模拟方法[14]。

本文依托杭州运河隧道工程，对泥水盾构下穿阶段上覆既有砌体建筑的沉降和裂缝进行了原位监测，总结了沉降发展规律和裂缝扩展特征，以期为泥水盾构下穿阶段上覆既有砌体结构的响应评估和保护控制提供工程实例参考。

1 监测方案及布置

杭州运河隧道工程采用2台长11.4 m、外径11.65 m的泥水盾构由东向西垂直穿越京杭运河，盾构主要穿越粉砂层、砂质粉土层和(淤泥质)粉质黏土层。衬砌外径11.3 m，由9块管片拼装而成。具体的泥水盾构施工技术及工程与水文地质条件等见文献[15]。

盾构穿越运河西岸排涝箱涵后，进入河西工作井之前，需邻近穿越2幢砌体结构仓库。为确保仓库结构安全，盾构穿越前后对仓库沉降及墙面裂缝进行了严密监测。

(1) 监测目的。通过监测了解盾构掘进过程中建筑物沉降及裂缝扩展情况，及时反馈设计，并决定是否采取辅助措施，确保建筑物的安全。

(2) 监测仪器及精度。建筑物沉降使用DiNi12精密电子水准仪、铟钢尺进行监测。DiNi12精密电子水准仪，精度为±0.7 mm/km；标准水准尺精度为1.0 mm；铟钢尺0.3 mm。

墙面裂缝宽度测量，对于较粗裂缝(>4 mm)，采用钢尺或游标卡尺；对于较细微裂缝(≤4 mm)，采用裂缝观测仪，精度为0.05 mm。裂缝扩展长度采用钢尺测量。

(3) 测点布设。用冲击钻在建筑物的基础或墙上钻孔，然后放入长200 mm～300 mm，直径φ20 mm～φ30 mm的半圆头弯曲钢筋，四周用水泥砂浆填实。监测点埋设的高度应方便监测，对测点应采取保护措施，避免受到破坏。

(4) 测量方法及计算。建筑物沉降用精密水准仪以二级沉降监测的精度(观测点测站高差中误差≤0.5 mm)来施测，组成变形监测的高程监测控制网。仪器在开始使用前均需检定，作业过程中严格遵守规范。每次观测都采用相同的观测仪器，相同的观测人员按相同的观测路线进行。

监测频率：掘进面前后<20 m时测1 次/d～2 次/d；掘进面前后<50 m时测1次/2d；掘进面前后>50 m时测1次/周。

隧道施工前，由监测基准点通过水准测量测出建筑物沉降监测点的初始高程H0，在隧道施工过程中测出的高程为Hn，则高差ΔH=Hn-H0，即为建筑物的沉降值。图1所示为河西岸边段地面及建筑物监测布置图。如图1所示，在1号仓库布置了16个沉降测点，编号分别为J1-1—J1-16；在2号仓库布置了6个沉降测点，编号分别为J2-1—J2-6。

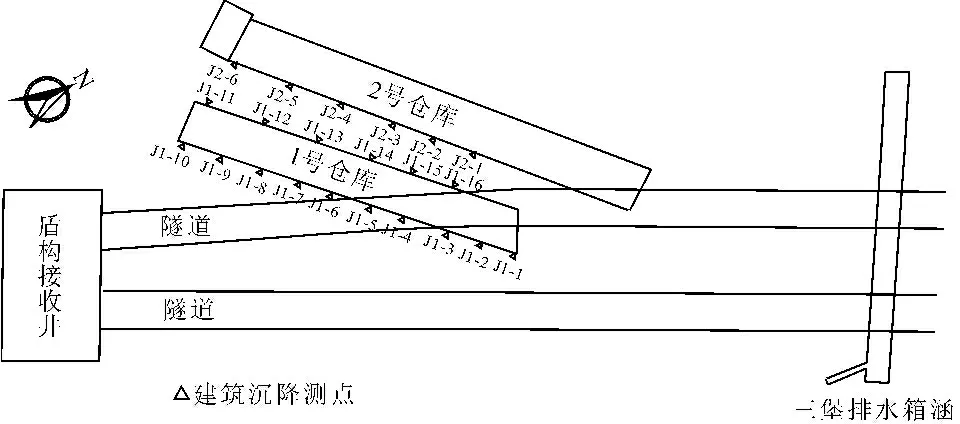
图1仓库沉降测点布置示意

图2所示为1号仓库和2号仓库现场图，图3所示为1号仓库纵向外墙图。现场勘查发现，1号、2号仓库均为1层砖混结构，沿纵墙分布16根柱子(宽40 cm，突出外墙面25 cm)，各柱均匀布置，轴线间距约3.8 m，檐口高度4.75 m。各柱之间外墙结构相同，均设置1窗(长1.5 m，高1.2 m)，窗底距地面2.9 m。

图2 1号、2号仓库现场图

图3 1号仓库外墙现场图

2 监测结果分析

现场实测发现，较之于2号仓库，1号仓库受盾构下穿的影响更为显著。本文仅对1号仓库因盾构下穿而引发的沉降和墙面裂缝的监测结果进行分析。

2.1 仓库墙体沉降

1号仓库沉降监测从2011年5月24日开始，一直延续至2011年7月8日。

图4所示为测点J1-1—J1-10监测沉降随盾构切口位置的变化曲线。图中横坐标y代表盾构切口与测点沿隧道纵向的水平距离，切口未到达测点位置时为负值，穿越测点位置即为正值。由图4中可见，盾构切口距离测点10 m至穿越离开30 m期间，测点沉降速度较大；此外，建筑物的响应相比十分微小。由此看来，盾构切口距离建筑物10 m至穿越离开30 m阶段，为建筑物沉降最为显著的阶段，该阶段需严密监测结构状况，是盾构穿越对上覆结构影响的关键环节。

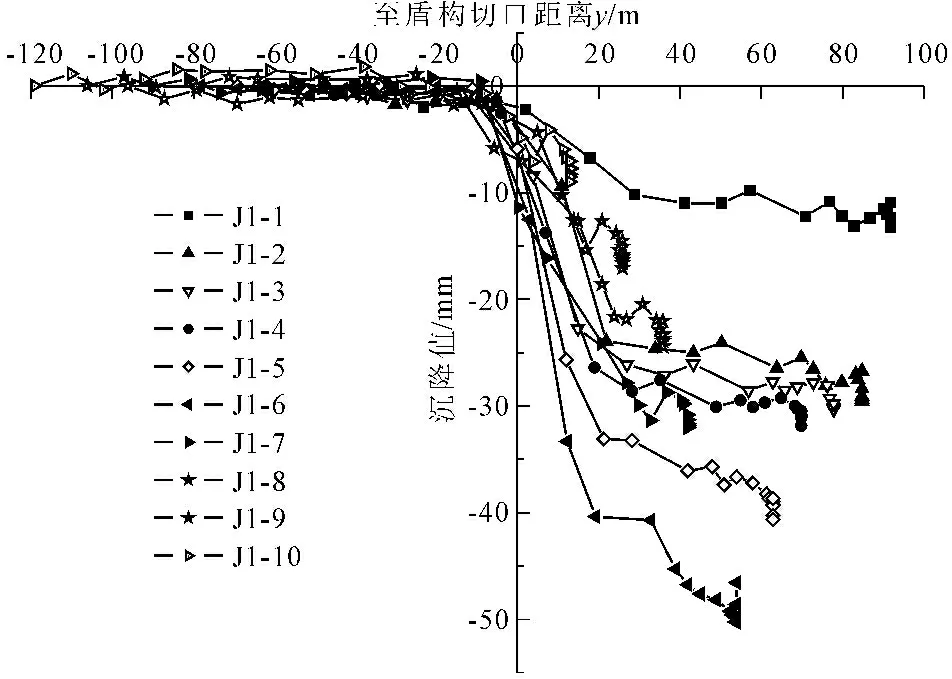
图4 1号仓库外墙沉降随盾构位置的变化

图5所示为测点J1-1—J1-10监测沉降随盾构切口位置的变化曲线。各测点沉降规律基本类似，在盾构穿越期间建筑沉降显著，约7 d之后，建筑位移微量变化，趋于稳定。至监测结束，沉降最大的测点依次为J1-6、J1-5、J1-7、J1-4、J1-3及J1-2，与隧道的垂直距离来看，这6个测点均位于隧道正上方或紧邻隧道。而测点J1-1、J1-8、J1-9及J1-10，距离隧道的垂直距离相对较远，其沉降也小得多。由此可见，距离隧道垂直距离越近，建筑物受盾构掘进影响产生的沉降越大，随距离的增大，所受影响呈削弱趋势。

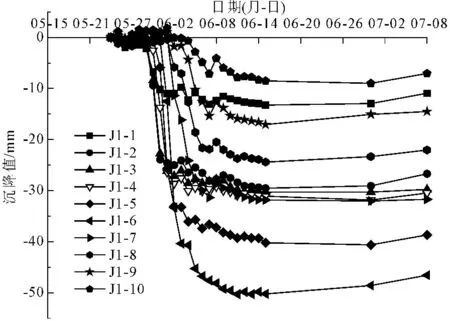
图5 1号仓库外墙沉降随时间的变化

2.2 仓库墙面裂缝

待盾构穿越后1号仓库位移基本稳定，对其墙面因盾构下穿和产生的裂缝进行了观测。依照现场观测情况，1号仓库邻近隧道一侧外墙面裂缝形状见图6，裂缝具体描述见表1。

C13所在墙面及C13四个角部位置均未见明显裂缝。Z14紧邻的后面的墙面，无论是窗角部还是整个墙面，均未发现明显裂缝，故图中略去不画。

图7为1号仓库纵墙典型裂缝图。

由图6和图7可见，裂缝在柱子上多水平扩展，而在墙面上以45°斜向扩展居多，墙面的门窗角部位置为裂缝的易发位置。对应于沉降监测较大的墙面，裂缝扩展较多；而对于沉降较小的墙面，如Z14至远离隧道方向的墙面，墙面受盾构掘进影响较小，未有明显裂缝。

3 结 语

本文实测研究了泥水盾构穿越阶段上覆既有砌体仓库的沉降与裂缝，主要有以下发现：

(1) 在盾构穿越期间仓库沉降显著，约7 d之后，仓库位移微量变化，趋于稳定；距离隧道越近，仓库沉降越大，随距离的增大，所受影响呈削弱趋势。

(2) 盾构掘进引起的仓库裂缝在柱子上多水平扩展，而在墙面上以45°左右斜向扩展居多，墙面的门窗角部位置为裂缝的易发位置。对应于沉降监测较大的墙面，裂缝扩展较多；而对于沉降较小的墙面，受盾构掘进影响较小，未见明显裂缝。

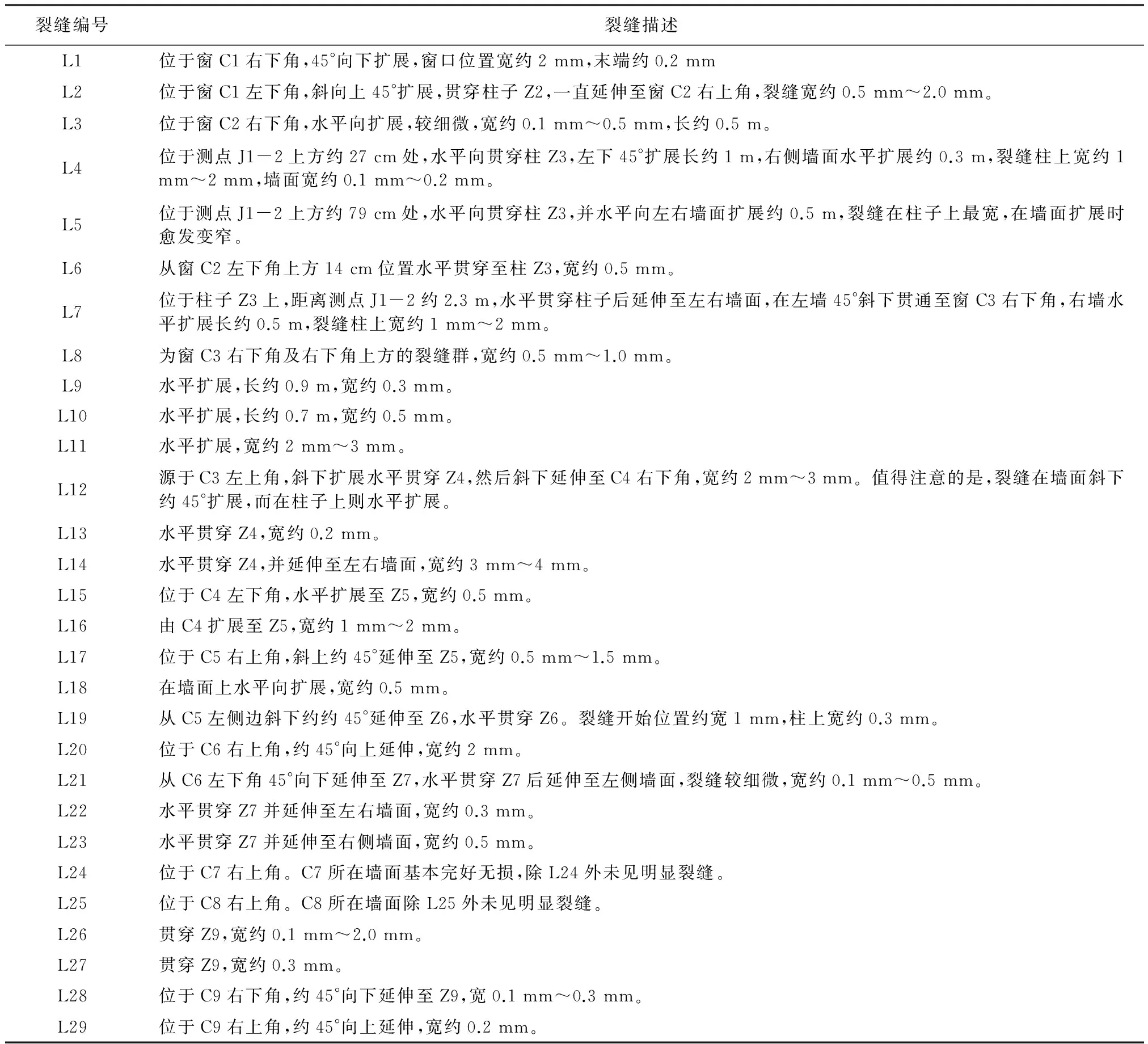
图6 1号仓库外墙面裂缝示意

续表1

图7 1号仓库纵墙面典型裂缝现场照片

参考文献：

[1] Burland J B, Wroth C P. Settlement of buildings and associated damage[C]//The British Society at Cambridge Proceeding of Conference on Settlement of Structures, London: Pentech Press, 1974:611-654.

[2] Boscardin M D, Cording E J. Building response to excavation-induced settlement[J]. Journal of Geotechnical Engineering, 1989,115(1):1-21.

[3] 夏 坤，凌 青，高益健.盾构法施工地面沉降预测分析研究[J].水利与建筑工程学报，2015，13(1):151-175.

[4] 刘冠男，许春虎，张永凯.盾构隧道施工引起海堤沉降的预测及控制[J].水利与建筑工程学报，2013，11(5):75-78.

[5] Potts D M, Addenbrooke T I. A structure's influence on tunnelling-induced ground movements[J]. Geotechnical Engineering, 1997,125(2):109-125.

[6] Franzius J N. Behaviour of Buildings Due to Tunnel Induced Subsidence[D]. London: Imperial College, 2004.

[7] Franzius J N, Potts D M, Addenbrooke T I, et al. The influence of building weight on tunnelling-induced ground and building deformation[J]. Soils and foundations, 2004,45(4):166-167.

[8] Franzius J N, Potts D M, Burland J B. The response of surface structures to tunnel construction[J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering, 2006,159(1):3-17.

[9] Deck O, Singh A. Analytical model for the prediction of building deflections induced by ground movements[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012,36(1):62-84.

[10] Boone S J. Ground-movement-related building damage[J]. Journal of Geotechnical Engineering, 1996,122(11):886-896.

[11] Finno R J, Voss Jr F T, Rossow E, et al. Evaluating damage potential in buildings affected by excavations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005,131(10):1199-1210.

[12] Schuster M, Kung G T C, Juang C H, et al. Simplified model for evaluating damage potential of buildings adjacent to a braced excavation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009,135(12):1823-1835.

[13] Dimmock P S, Mair R J. Effect of building stiffness on tunnelling-induced ground movement[J]. Tunnelling and Underground Space Technology, 2008,23(4):438-450.

[14] Giardina G, Marini A, Hendriks M A N, et al. Experimental analysis of a masonry facade subject to tunnelling-induced settlement[J]. Engineering Structures, 2012,45:421-434.

[15] 林存刚，吴世明，张忠苗，等.粉砂地层泥水盾构刀盘脱困工程实例分析[J].岩石力学与工程学报，2013，31(S1):2897-2906.